Caténoïde
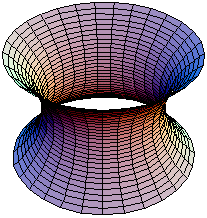
La caténoïde (prononciation : /ka.te.nɔ.id/ Écouter) (du latin catena, « chaîne ») est une surface minimale entre deux cercles. Dans le cas où ces deux cercles sont coaxiaux, c'est aussi la figure obtenue par révolution d'une chaînette autour de l'axe commun de ces deux cercles.
C'est, avec le plan, la seule surface minimale de révolution. Elle fut découverte par Leonhard Euler en 1744.
Elle a pour équations paramétriques :
où cosh représente la fonction cosinus hyperbolique.

Il suffit, pour obtenir une représentation matérielle d'une caténoïde, de tremper deux cercles accolés dans de l'eau savonneuse, puis de percer la bulle centrale avant d'écarter lentement les deux cercles. Le film de savon qui se forme sur cette armature est une caténoïde.

