Dualité (géométrie projective)

Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pour les articles homonymes, voir Dualité (mathématiques) et Dualité.

La dualité projective, créée par Jean-Victor Poncelet (1788 - 1867), père fondateur de la géométrie projective, bien que beaucoup moins enseignée que la dualité en algèbre linéaire, est probablement la plus belle notion de dualité que l'on rencontre en mathématiques.

Il s'agit de formaliser la constatation toute simple qu'il y a une analogie - une dualité, justement - entre le fait que par deux points distincts passe une droite et une seule, et le fait que deux droites distinctes se coupent en un point et un seul (à condition de se placer justement en géométrie projective, de sorte que deux droites parallèles se rencontrent en un point à l'infini).

Dualité dans un plan projectif

Définition

Contrairement à la géométrie plane classique où les droites sont des ensembles de points, il vaut mieux considérer en géométrie projective que le plan projectif $P$ est constitué d'un ensemble de points $\ \mathcal P(P)$, d'un ensemble de droites $\mathcal D(P)$, et d'une relation indiquant quels points sont sur quelle droite (ou quelles droites passent par quel point). Pour bien comprendre que c'est cette relation qui est importante et non la nature des points et des droites, le mathématicien Hilbert disait : « Il faut toujours pouvoir dire "table", "chaise" et "bock de bière" à la place de "point", "droite" et "plan" » !

Nous considérons dans un premier temps que le plan projectif $P$ est défini de manière axiomatique ; on constate alors que l'on obtient un autre plan projectif en considérant l'objet $P*$ dont les "points" sont les droites de $P$ et les "droites" sont les points de $P$, une droite de $P*$ (qui est un point $M$ de $P$) passant par un "point" de $P*$ (qui est une droite $D$ de $P$) lorsque $D$ passe par $M$.

Voici un point et une droite de $P$ : normal !	Voici un "point" et une "droite" de $P*$ dont nous avons dessiné 4 de ses "points".

Pour simplifier, au lieu de travailler sur 2 plans différents, $P$ et $P*$, on peut se contenter de travailler sur un seul plan projectif $P$.

Corrélation ou dualité, déf : Une corrélation est une transformation des points du plan en droites et des droites du plan en points et qui respecte l'incidence.

Polarité, déf : Une polarité est une corrélation involutive, c’est-à-dire que son carré est la transformation identique.

Exemples

À toute configuration de points et de droites dans $P$ correspond alors dans $P*$ une configuration duale obtenue en échangeant les points et les droites, et de même, à tout théorème dans $P$, correspond un théorème dual. Voici quelques exemples :

Configuration dans $P$	Même configuration vue dans $P*$
2 points $A$ et $B$ et la droite passant par ces deux points, notée $(AB)$	2 droites $A$ et $B$ et leur point d'intersection, noté $A\cap B$ (la notation $(AB)$ paraîtrait trop étrange)
3 points alignés	3 droites concourantes
Configuration de Ceva Un triangle de sommets $A,B,C$ et trois céviennes $D,E,F$ concourant en $M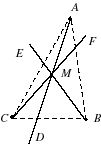$	Configuration de Ménélaus Un triangle de côtés $A,B,C$ et une ménélienne $M$ rencontrant les côtés en $D,E,F$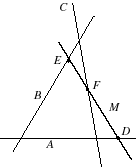
Configuration de Desargues Deux triangles de sommets respectifs $A,B,C$ et $A',B'C'$, et de côtés $D,E,F$ et $D',E',F'$ ($D=(BC), E=(CA)$ etc), $P,Q,R$ les points $D\cap D'$, $E\cap E'$, $F\cap F'$, $U,V,W$ les droites $(AA'), (BB'), (CC')$. Le théorème de Desargues affirme que $P,Q,R$ sont alignés ssi $U,V,W$ sont concourantes.	Configuration de Desargues (qui est donc "auto-duale") Deux triangles de côtés respectifs $A,B,C$ et $A',B'C'$, et de sommets $D,E,F$ et $D',E',F'$ ($D=B\cap C, E=C\cap A$ etc), $P,Q,R$ les droites $(DD')$, $(EE')$, $(FF')$, $U,V,W$ les points $(A\cap A'), (B\cap B'), (C\cap C')$. Le théorème de Desargues affirme que $P,Q,R$ sont concourantes ssi $U,V,W$ sont alignés.
Configuration de Pappus Deux triplets de points alignés $A,B,C$ et $A',B',C'$, $P=(BC') \cap (B'C) , Q=(CA') \cap (C'A)$, $P=(AB') \cap (A'B)$ ; le théorème de Pappus affirme que $P,Q,R$ sont alignés.	Configuration de "Copappus", ou Pappus-dual Deux triplets de droites concourantes $A,B,C$ et $A',B',C'$, $P=(B\cap C', B'\cap C) , Q=(C\cap A',C'\cap A)$, $P=(A\cap B', A'\cap B)$ ; le théorème de "Copappus" affirme que $P,Q,R$ sont concourantes. (voir figure ci-dessous où on voit que cette configuration est finalement "auto-duale" également)

Remarque : Si l'on convient d'identifier une droite avec l'ensemble de ses points, il faut, pour que la dualité soit parfaite, identifier un point avec l'ensemble des droites qui passent par ce point, autrement dit, identifier un faisceau de droites avec son pôle !

Dualités, corrélations et polarités

Considérons les homographies de $P$ sur $P*$ ; ce sont des bijections $f$ de $\mathcal P(P)$ sur $\mathcal P(P^*)=\mathcal D(P)$ qui transforment une droite de $P$ en une "droite" de $P*$ ; on peut donc les prolonger en une bijection, toujours notée $f$, de $\mathcal P(P)\cup \mathcal D(P)$, qui transforme un point en une droite et réciproquement, et qui vérifie : $M \in D \iff f(D) \in f(M)$.

De telles applications sont appelées des dualités ou corrélations ; lorsqu'elles sont involutives ($f=f^{-1}$), elles sont appelées des polarités ou autrefois "transformations par polaires réciproques". Dans ce dernier cas, l'image d'un point est appelé la polaire de ce point, et l'image d'une droite, son pôle.

D'après le théorème fondamental de la géométrie projective, dans le cas réel toute dualité provient d'une homographie (dans le cas général, d'une semi-homographie).

Théorème d'incidence et de réciprocité

Il y a deux théorèmes importants qui découlent des définitions.

Théorème d'incidence: Si le point A est incident à la droite d, alors le point dual de d est incident à la droite duale de A.

Théorème de réciprocité polaire: Si le point A est sur la polaire du point B, alors B est sur la polaire de A. Ce théorème est plus puissant que le précédent.

Relations avec la dualité en algèbre linéaire

On sait qu'il existe une bijection entre les points de $P$ et les droites vectorielles d'un espace vectoriel $E$ de dimension 3, et une bijection entre les droites de $P$ et les plans vectoriels de $E$ (un point appartenant à une droite si la droite vectorielle est incluse dans le plan vectoriel).

L'orthogonalité entre $E$ et son dual $E*$, ensemble des formes linéaires sur $E$, qui à tout sous-espace vectoriel de $E$ associe un sous-espace vectoriel de $E*$ induit une bijection entre les plans vectoriels de $E$ et les droites vectorielles de $E*$, et entre les droites vectorielles de $E$ et les plans vectoriels de $E*$, qui inverse les inclusions.

Il existe donc une bijection canonique entre les points et droites de $P*$ et les droites et plans vectoriels de $E*$ qui respecte les incidences : si un plan projectif $P$ est associé à un espace vectoriel $E$, le plan dual $P*$ est bien associé à l'espace vectoriel dual $E*$.

Duale d'une homographie

Une homographie $f$ du plan projectif dans lui-même est une bijection dans l'ensemble des points de $P$, qui induit une bijection $f*$ dans l'ensemble des droites de $P$, qui est l'ensemble des "points" de $P*$ : $f*$ est l'homographie duale de $f$ (remarquons que $f*(D)=f(D)$ !) ; on vérifie que si $f$ provient d'un automorphisme $\vec f$ de $\vec E$, alors $f*$ provient de l'automorphisme de $\vec E^*$ dual de $\vec f$, appelé plus souvent automorphisme transposé de $f$.

Utilisation des coordonnées

Rapportons le plan projectif $P$ à un repère projectif $R=(A_1,A_2,A_3,\Omega)\,$, qui est associé à une base $B=(e_1,e_2,e_3)\,$ de l'espace vectoriel $E$ ; considérons l'isomorphisme $\varphi$ entre $E$ et son dual qui transforme $B$ en la base duale $B^*=(e_1^*,e_2^*,e_3^*)\,$, lequel induit une dualité entre $P$ et $P*$ ; à un point $M$ de $P$ est associé un vecteur défini à une constante multiplicative près de coordonnées $(a,b,c)$ dans $B$ (les coordonnées homogènes de $M$ dans $R$), auquel est associé par $\varphi$ la forme linéaire $ax+by+cz$ dont le noyau est le plan d'équation $ax+by+cz=0$ ;

cette équation est l'équation homogène de la droite $D$ image de $M$ par la dualité ; l'on vérifie qu'inversement, l'image de $D$ est $M$, ce qui fait que cette dualité est une polarité, définie par :

point de coordonnées homogènes $(a,b,c)$ ↔ droite d'équation homogène : $ax+by+cz=0$

le repère dual $R=(A_1^*,A_2^*,A_3^*,\Omega^*)\,$ de $R$, associé à $B*$ est formé des droites d'équation respectives : $x=0,y=0,z=0,x+y+z=0$, donc $A_1^*=(A_2A_3), A_2^*=(A_3A_1), A_3^*=(A_1A_2)\,$. Remarquons qu'un point et sa droite polaire ont mêmes coordonnées homogènes, l'un dans $R$, l'autre dans $R*$.

Dualité associée à une forme bilinéaire, polarité associée à une forme quadratique ou à une conique

Soit $f$ une dualité de $P$ vers $P*$ provenant d'un isomorphisme $\vec f$ de $E$ vers $E*$. Il est associé à ce dernier une forme bilinéaire non dégénérée sur $E$, définie par $\varphi (x,y) = \vec f (y)(x)$ (noté par le crochet de dualité $<x,\vec f (y)>$) et cette correspondance est bijective ; la dualité $f$ est dite associée à la forme bilinéaire $\varphi$ (définie à une constante multiplicative près). La matrice de l'isomorphisme $\vec f$ dans une base $B$ et la base duale $B*$ est celle de la forme bilinéaire $\varphi$dans $B$.

La dualité $f$ est une polarité ssi pour tous points $M$ et $N$ : $M\in f(N) \iff N\in f(M)$, ce qui se traduit sur la forme bilinéaire $\varphi$ par : pour tous vecteurs $x$ et $y$ : $\varphi(x,y)=0 \iff \varphi(y,x)=0$ ; on montre que cette dernière condition équivaut à ce que $\varphi$ soit symétrique ou antisymétrique (si le corps est de caractéristique différente de 2).

Toute forme quadratique sur $E$ engendre une forme bilinéaire symétrique, laquelle en engendre une polarité dans $P$, qui est dite associée à $q$. Le cône isotrope de $q$ (défini par $q(x)=\varphi(x,x)=0$) est un cône du second degré de $E$ lequel engendre une conique projective $(C)$ dans $P$. On dit alors par abus que la polarité $f$ associée à $q$ est la polarité par rapport à (C). Remarquons qu'on a alors : $M\in (C) \iff M\in f(M)$.

Polarité par rapport à un cercle dans le plan euclidien

Considérons un cercle (C) de centre O de rayon a d'un plan euclidien $\breve P$ rapporté à un repère orthonormé $(O,e_1,e_2)\,$ ; $P$ est le complété projectif de $\breve P$ et $E$ son enveloppe vectorielle, rapportée à $(O,e_1,e_2,e_3)\,$.

L'équation cartésienne du cercle est $x^2+y^2=a^2$ ; la polarité $f$ par rapport à $(C)$ est donc associée à la forme quadratique $X^2+Y^2-a^2Z^2$ de $E$ et l'isomorphisme de $E$ sur $E*$ est celui qui envoie $(O,e_1,e_2,e_3)\,$ sur $(O,e_1^*,e_2^*,-ae_3^*)$

Du point de vue du plan affine $\breve P$, la polarité $f$ a une définition très simple : au point de coordonnées $(u,v)$ correspond la droite d’équation $ux+vy=a^2$ et l’image d’un point à l’infini est la droite passant par $O$ et perpendiculaire à la direction du point.

Et on a les définitions géométriques suivantes : la polaire (droite image par la polarité) d’un point $M_0(u,v)$ par rapport au cercle (C) est le lieu des conjugués harmoniques du point par rapport au cercle, lieu défini par la relation $\overrightarrow {OM}\overrightarrow {OM_0}=ux+vy=a^2$ ; c’est la droite orthogonale à la droite $(OM_0)$ passant par l’inverse de $M_0$ par rapport à (C) ; c’est aussi l’axe radical du cercle (C) et du cercle de diamètre $[O M_0]$ ; quand $M_0$ est extérieur à $(C)$, c’est la droite qui joint les points de contact des tangentes issues de $M_0$ au cercle (C).

Dualité entre courbes

Article détaillé : courbe duale.

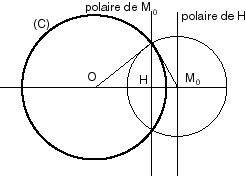
Une dualité, qui transforme des points en droites et réciproquement, transforme une courbe $(\Gamma_0)$ ( famille de points) de $P$ en une "courbe" (famille de droites) du plan dual $P*$: mais grâce à la notion d'enveloppe, on retrouve une courbe (famille de points) de $P$ : l'enveloppe de la famille des droites duales, dite courbe duale de $(\Gamma_0)$. Ce qui est remarquable, c'est que lorsque la dualité est une polarité, la duale de la duale est la courbe de départ (autrement dit, la famille des droites polaires des points de la courbe duale enveloppe la courbe de départ). Ci-contre, une figure illustrant ceci, avec une polarité par rapport à un cercle $(C)$. Cette transformation est une transformation de contact : si une famille de courbes admet une enveloppe, la famille des courbes polaires admet pour enveloppe la polaire de cette enveloppe. Voir ici pour plus de détails.

Configuration de Pappus, exemple détaillé de dualité

Pour illustrer géométriquement une dualité quelconque, il faut définir le processus par lequel on transforme un point en droite. Un exemple de dualité simple est donné ci-dessous: on prend le quadrangle (4 points) ACZF, on le transforme en quadrilatère (4 droites) aczf, et pour compléter un peu la figure les droites AC, CZ, ZF de la figure de départ ont été tracées, ainsi que les points d'intersection a*c, c*z et z*f de la figure d'arrivée.

Poursuivant le dessin du même exemple, on peut figurer la dualité d'une configuration de Pappus, voir Théorème de Pappus. La configuration de départ est formée des 9 points: AEC DBF XYZ, la configuration d'arrivée est donnée par les 9 droites aec dbf xyz. Dans la configuration de départ on a pris soin de compléter la figure par les 9 droites joignant les points, il s'agit des droites jnp qhk et mgr; de même dans la configuration d'arrivée les intersection des droites donnent naissance aux 9 points JNP QHK MGR.

Dualité dans un espace projectif de dimension finie

C'est la généralisation de ce que nous venons de voir dans le plan ; en dimension $n$, non seulement la dualité échange les points et les hyperplans, mais plus généralement les sous-espaces de dimension $k$ avec ceux de dimension $n-1-k$.

Par exemple, en dimension 3, les points sont échangés avec les plans, et les droites avec elles-mêmes. Le théorème dual de : "par deux points distincts" passe une droite et une seule devient : "deux plans distincts se coupent en une droite". Un tétraèdre de sommets $ABCD$ devient par dualité un tétraèdre de faces $ABCD$ ; dans le premier cas, les points $A$ et $B$ déterminent une arête (celle qui passe par $A$ et $B$, et dans le deuxième aussi (l'intersection de $A$ et $B$).

Plus précisément le dual $E*$ d'un espace projectif $E$ de dimension $n$ est l'espace dont les sous-espaces de dimension $k$ sont les duaux de ceux de dimension $n-1-k$ de $E$, et une dualité sur $E$ est une bijection de l'ensemble des sous-espaces projectifs de $E$ dans lui-même qui inverse les inclusions et transforme un sous-espace de dimension $k$ en un de dimension $n-1-k$ ; dans le cas réel, une dualité provient d'une homographie de $E$ sur $E*$ (d'une semi-homographie dans le cas général).

Tout ce qui a été vu dans le cas plan se généralise ici, en particulier la notion de polarité par rapport à une conique qui devient ici celle de polarité par rapport à une hyperquadrique (non dégénérée).

Références

• Alain Bigard, Géométrie, Masson, 1998
• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, ISBN 978-2-91-635208-4
• Jean Frenkel, Géométrie pour l'élève professeur, Hermann, 1973
• Bruno Ingrao, Coniques projectives, affines et métrique, C&M, ISBN 978-2916352121
• Jean-Claude Sidler, Géométrie projective, Interéditions, 1993
• H.S.M. Coxeter, Projective geometry, Springer, 1998(3^e édition); c'est en anglais canadien très facile à comprendre, et les pages sur la dualité et la polarité sont claires, bien que très abstraites.
• Yves Ladegaillerie, Géométrie, Ellipses, 2003