Loi des sinus

En trigonométrie, la loi des sinus est une relation de proportionnalité entre les longueurs des côtés d'un triangle et les sinus des angles respectivement opposés. Elle permet, connaissant deux angles et un côté, de calculer la longueur des autres côtés.

Il existe une formule des sinus de présentation analogue en trigonométrie sphérique.

Ces lois sont énoncées et démontrées, pour la forme sphérique, par Abu Nasr Mansur au début du XI^e siècle et, pour la forme plane, par Nasir al-Din al-Tusi au début du XIII^e siècle^[1].

Loi des sinus en géométrie plane[modifier | modifier le code]

Énoncé[modifier | modifier le code]

On considère un triangle quelconque ABC, représenté sur la Fig. 1 ci-contre, où les angles sont désignés par les minuscules grecques et les côtés opposés aux angles par la minuscule latine correspondante :

a = BC et α = angle formé par [AB] et [AC] ;
b = AC et β = angle formé par [BA] et [BC] ;
c = AB et γ = angle formé par [CA] et [CB].

La formule dite des sinus est alors :

\,{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}

,

On a même mieux :

\,{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={\frac {abc}{2S}}=2R

,

où R est le rayon du cercle circonscrit au triangle ABC et

S={\sqrt {p(p-a)(p-b)(p-c)}}

est l'aire du triangle donnée à partir du demi-périmètre p par la formule de Héron.

La relation de proportionnalité est parfois résumée ainsi :

a:b:c=\sin \alpha :\sin \beta :\sin \gamma

Le théorème peut être utilisé

pour déterminer le rayon du cercle circonscrit
$\,R={\frac {a}{2\sin \alpha }}$
pour résoudre un triangle dont on connaît deux angles et un côté.

Démonstrations[modifier | modifier le code]

En exprimant une hauteur de deux manières[modifier | modifier le code]

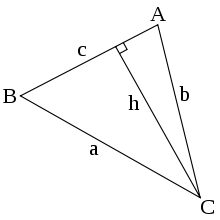
On considère un triangle de côtés a, b, et c, et α, β, γ ses angles aux sommets A, B, et C respectivement. La hauteur issue de C divise le triangle ABC en deux triangles rectangles. Notons h cette hauteur ; on peut appliquer la définition du sinus dans les deux petits triangles rectangles pour exprimer h :

\sin \alpha ={\frac {h}{b}}{\text{ et }}\sin \beta ={\frac {h}{a}}.

Dont on tire deux expressions pour h :

h=b\sin \alpha =a\sin \beta \,

et donc :

{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}.

En faisant de même avec la hauteur issue de A on obtient :

{\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.

Par le calcul de l'aire du triangle[modifier | modifier le code]

L'aire S du triangle peut se calculer en choisissant le côté AB = c comme base et h comme hauteur. On obtient alors :

S={\frac {c\times h}{2}}={\frac {c\times b\sin \alpha }{2}}.

En multipliant par ${\tfrac {a}{S\sin \alpha }}$ , on en déduit :

{\frac {a}{\sin \alpha }}={\frac {abc}{2S}}.

Par symétrie des notations,

{\frac {b}{\sin \beta }}={\frac {abc}{2S}}\quad {\rm {et}}\quad {\frac {c}{\sin \gamma }}={\frac {abc}{2S}}.

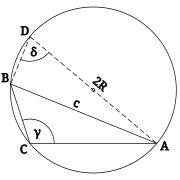
Par le théorème de l'angle inscrit[modifier | modifier le code]

Fig. 3. $γ = δ$ et $sin γ = sin δ = c / 2 R$ .
Fig. 4. $γ = π - δ$ et $sin γ = sin δ = c / 2 R$ .
Fig. 5. $γ = π / 2$ .

En remplaçant $C$ par le point $D$ diamétralement opposé à $A$ sur le cercle circonscrit, on trouve (Fig. 3 et 4)^[2]^,^[3] :

\sin \gamma ={\frac {c}{2R}}\quad {\rm {donc}}\quad {\frac {c}{\sin \gamma }}=2R.

Si $A$ et $B$ sont diamétralement opposés, cette construction n'est pas possible mais l'égalité est immédiate (Fig. 5).

On démontre de même que

{\frac {b}{\sin \beta }}=2R\quad {\rm {et}}\quad {\frac {a}{\sin \alpha }}=2R.

Formule des sinus en trigonométrie sphérique[modifier | modifier le code]

On considère un triangle $ABC$ sur une sphère de centre O. On note α (respectivement β et γ) l'angle du triangle au sommet A (respectivement B et C). On note a, b et c les angles sous-tendus au centre O de la sphère par la partie de grand cercle correspondante. Ainsi a désigne l'angle BOC, etc. Bien entendu les longueurs des côtés se déduisent de a, b et c en les multipliant par le rayon de la sphère.

La formule des sinus s'énonce alors de la manière suivante : ${\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}.$

Elle met en évidence une dualité entre les angles au centre et les angles aux sommets.

En dimensions supérieures[modifier | modifier le code]

Plus généralement, pour un n-simplexe (par exemple un tétraèdre ( $n = 3$ ), un pentachore ( $n = 4$ ), etc. ; le triangle correspond au cas n = 2) d'un espace euclidien de dimension n, la valeur absolue du sinus polaire de l'ensemble des vecteurs normaux aux faces autour d'un sommet, divisée par l'aire de la face opposée à ce sommet, ne dépend pas de ce sommet, et vaut ${\frac {(nV)^{n-1}}{(n-1)!P}}$ , où V est le volume du simplexe, et P le produit des aires de ses faces.

Notes et références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Law of sines » (voir la liste des auteurs).

↑ Marie-Thérèse Debarnot, « Trigonométrie », dans Roshdi Rashed (dir.), Histoire des sciences arabes : Mathématiques et physiques, t. 2, Seuil, 1997, p. 161-198, pp. 173 et 184
↑ R. Bastin, B. Baudelet, S. Bouzette et P. Close, Maths 4, de Boeck, coll. « Adam », 2009 (ISBN 978-2-80410143-5, lire en ligne), p. 241-242.
↑ « Loi des sinus – Une démonstration simple », sur blogdemaths.wordpress.com, 2011.

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Loi des sinus, sur Wikimedia Commons

Liens externes[modifier | modifier le code]

(en) Eric W. Weisstein, « Law of Sines », sur MathWorld
(en) Eric W. Weisstein, « Generalized Law of Sines », sur MathWorld

Articles connexes[modifier | modifier le code]

Trigonométrie :
- sinus ;
- fonction trigonométrique ;
- trigonométrie sphérique ;
- triangulation.
Géométrie du triangle :

Portail de la géométrie

[1] Marie-Thérèse Debarnot, « Trigonométrie », dans Roshdi Rashed (dir.), Histoire des sciences arabes : Mathématiques et physiques, t. 2, Seuil, 1997, p. 161-198, pp. 173 et 184

[2] R. Bastin, B. Baudelet, S. Bouzette et P. Close, Maths 4, de Boeck, coll. « Adam », 2009 (ISBN 978-2-80410143-5, lire en ligne), p. 241-242.

[3] « Loi des sinus – Une démonstration simple », sur blogdemaths.wordpress.com, 2011.

[1]

[2]

[3]

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron