Équations de Navier-Stokes

En mécanique des fluides, les équations de Navier-Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides newtoniens (donc des gaz et de la majeure partie des liquides[a]). La résolution de ces équations modélisant un fluide comme un milieu continu à une seule phase est difficile, et l'existence mathématique de solutions des équations de Navier-Stokes n'est pas démontrée. Mais elles permettent souvent, par une résolution approchée, de proposer une modélisation de nombreux phénomènes, comme les courants océaniques et des mouvements des masses d'air de l'atmosphère pour les météorologistes, le comportement des gratte-ciel ou des ponts sous l'action du vent pour les architectes et les ingénieurs, ou encore celui des avions, des trains ou des voitures à grande vitesse pour leurs bureaux d'études concepteurs, ainsi que l'écoulement de l'eau dans un tuyau et de nombreux autres phénomènes d'écoulement de divers fluides.
Ces équations sont nommées ainsi pour honorer les travaux de deux scientifiques du XIXe siècle : le mathématicien et ingénieur des Ponts Henri Navier, qui le premier a introduit la notion de viscosité dans les équations d'Euler en 1822[1], et le physicien George Gabriel Stokes, qui a donné sa forme définitive à l'équation de conservation de la quantité de mouvement en 1845[2],[3]. Entre-temps, divers scientifiques ont contribué à l'avancement du sujet : Augustin Louis Cauchy[4], Siméon Denis Poisson en 1829[5] et Adhémar Barré de Saint-Venant en 1843.
Pour un gaz peu dense, il est possible de trouver une solution approchée de l’équation de Boltzmann, décrivant le comportement statistique des particules dans le cadre de la théorie cinétique des gaz. Ainsi, la méthode de Chapman-Enskog, due à Sydney Chapman et David Enskog en 1916 et 1917, permet de généraliser les équations de Navier-Stokes à un milieu comportant plusieurs espèces et de calculer l'expression des flux de masse (équations de Stefan-Maxwell incluant l'effet Soret), de quantité de mouvement (en donnant l'expression du tenseur de pression) et d'énergie en montrant l'existence de l'effet Dufour. Cette méthode permet également de calculer les coefficients de transport à partir des potentiels d'interaction moléculaires.
La résolution mathématiquement rigoureuse des équations de Navier-Stokes constitue l'un des problèmes du prix du millénaire.
Cet article décrit diverses variantes des équations valables pour des milieux de composition homogène, les problèmes liés à la diffusion et aux réactions chimiques n'y sont pas abordés[6].
Lois de conservation[modifier | modifier le code]
Notations et relations utilisées[modifier | modifier le code]
On utilise les notations conformes à la norme ISO/CEI 80000-2[7]
- Les caractères en gras sans serif comme désignent des tenseurs.
- est l'opérateur nabla exprimé dans un système de coordonnées cartésiennes.
- est l'opérateur gradient exprimé dans un système de coordonnées cartésiennes.
- est l'opérateur divergence exprimé dans un système de coordonnées cartésiennes.
- désigne l'opérateur rotationnel exprimé dans un système de coordonnées cartésiennes. Il est parfois noté .
- est l'opérateur laplacien exprimé dans un système de coordonnées cartésiennes.
- est le laplacien vectoriel, soit le vecteur dont chaque composante est le laplacien de la même composante de .
- Note : diffère de . Toutefois, ne prête plus à confusion.
- Le produit dyadique de deux vecteurs s'écrit
- où × est le produit matriciel.
- Le produit doublement contracté : est l'opérateur défini par :
- où Tr représente l'opérateur trace.
Quelques identités vectorielles utiles pour cet article (les deux dernières généralisent la notion de divergence aux tenseurs de rang deux) :
Loi de conservation[modifier | modifier le code]
On peut définir une loi de conservation pour une variable extensive de densité ϕ entraînée à la vitesse et comportant un terme de production volumique S par :
- .
Formulation eulérienne[modifier | modifier le code]
La formulation la plus utilisée fait appel à un référentiel fixe naturel lorsque l'on traite un problème stationnaire ou instationnaire dans lequel le domaine de calcul est connu à l'avance. On fait alors appel aux variables eulériennes.
On obtient les équations de Navier-Stokes en appliquant la relation de conservation ci-dessus à la masse volumique ρ, à la quantité de mouvement et à l'énergie totale ρ E[8].
- Équation de continuité (équation de bilan de la masse)
- Équation de bilan de la quantité de mouvement
- Équation de bilan de l'énergie
Dans ces équations :
- t représente le temps (unité SI : s) ;
- ρ désigne la masse volumique du fluide (unité SI : kg m−3) ;
- désigne la vitesse eulérienne d'une particule fluide (unité SI : m s−1) ;
- désigne le tenseur des contraintes (ou tenseur de pression) qui, si on néglige le rayonnement, se décompose en :
- ;
- désigne le tenseur des contraintes visqueuses (unité SI : Pa) ;
- désigne le tenseur unité ;
- p désigne la pression thermodynamique (unité SI : Pa) ;
- désigne la gravité ou toute autre force massique extérieure (unité SI : m s−2) ;
- E désigne l'énergie totale par unité de masse (unité SI : J kg−1) ; elle s'exprime en fonction de l'énergie interne par unité de masse e par :
- ;
- désigne le flux de chaleur dû à la conduction thermique (unité SI : J m−2 s−1) ;
- désigne le flux de chaleur dû au rayonnement (unité SI : J m−2 s−1).
Afin de clore le système il est nécessaire de décrire p, Σ, et à partir d'hypothèses sur le fluide considéré. est quant à lui l'objet d'un calcul de transfert radiatif éventuellement couplé à la résolution des équations de Navier-Stokes.
Quelques variations autour du système d'équations[modifier | modifier le code]
- On peut exprimer différemment l'équation de quantité de mouvement en remarquant que :
- .
L'équation alors obtenue s'interprète comme la deuxième loi de Newton, en remarquant que le terme décrit l’accélération des particules du fluide.
- Il est possible d'exprimer la conservation de l'énergie sous forme équivalente en transférant au premier membre le terme correspondant à la pression :
- .
- Le terme ρ E + p peut être remplacé par où h = e + pρ est l'enthalpie massique.
- En multipliant scalairement l'équation de quantité de mouvement écrite comme ci-dessus par la vitesse on obtient une loi de conservation pour l'énergie cinétique :
- .
- En soustrayant cette équation de l'équation de conservation de l'énergie, en utilisant l'équation de conservation de la masse et l'identité
- ,
- on obtient l'équation suivante sur l'énergie interne par unité de masse :
- .
Formulation lagrangienne[modifier | modifier le code]
Dans certains problèmes le domaine occupé par le fluide peut varier considérablement au cours du temps. Il s'agit donc de problèmes instationnaires. C'est le cas dans les problèmes d'explosion ou en astrophysique. On fait alors appel aux variables lagrangiennes définies dans le repère noté ξ. L'accélération de la particule fluide est donnée par la dérivée particulaire :
- .
Le dernier terme de cette équation est le terme d'advection de la quantité ϕ. Celle-ci peut être scalaire, vectorielle ou tensorielle.
Pour la quantité de mouvement, la dérivée particulaire vaut :
- .
Les équations de conservation dans le système de coordonnées définies par s'écrivent :
- Équation de continuité (ou équation de bilan de la masse)
- Équation de bilan de la quantité de mouvement
- Équation de bilan de l'énergie
Expressions dans des systèmes de coordonnées[modifier | modifier le code]
En utilisant l'expression des opérateurs dans les divers systèmes courants de coordonnées il est possible de détailler les expressions des équations.
Expression en coordonnées cartésiennes
Expression en coordonnées cylindriques
Expression en coordonnées sphériques
Repère en translation et rotation[modifier | modifier le code]
Il est parfois utile de décrire la dynamique des fluides dans un repère non galiléen, par exemple en physique de l'atmosphère ou pour décrire le mouvement d'un fluide dans un réservoir mobile, par exemple dans un lanceur.
On considère un repère orthonormé se déplaçant à la vitesse par rapport au repère fixe et ayant une vitesse de rotation dans celui-ci.
Pour un point situé en dans le repère mobile, la formule de Varignon s'écrit :
Par dérivation, on obtient l'accélération apparente dans le repère mobile :
Le premier terme dans le crochet est l'accélération de Coriolis et le deuxième est le terme centripète. Le troisième correspond au déplacement du repère mobile :
Il existe donc un terme à ajouter au premier membre de l'équation de la quantité de mouvement. Ce terme est d'ordre cinétique : il ne correspond pas à une force réelle et n'influence donc pas l'équation de conservation de l'énergie.
Fluide newtonien, hypothèse de Stokes[modifier | modifier le code]
En première approximation, pour de nombreux fluides usuels comme l'eau et l'air, le tenseur des contraintes visqueuses est proportionnel à la partie symétrique du tenseur des taux de déformation (hypothèse du fluide newtonien).
- μ désigne la viscosité dynamique du fluide (unité : Poiseuille (Pl) = Pa s = N m−2 s.)
- μ' désigne la seconde viscosité (ou viscosité volumique, en anglais volume viscosity) du fluide (unité : Poiseuille (Pl) = Pa s = N m−2 s).
Ces coefficients dépendent en général de la masse volumique et de la température thermodynamique, comme au paragraphe suivant.
Avec l'expression du tenseur des contraintes visqueuses, l'équation de quantité de mouvement prend la forme :
- .
En supposant que les variations spatiales de et sont négligeables, on obtient
- ,
dont on déduit
On utilise généralement l'hypothèse de Stokes pour relier la viscosité dynamique à la seconde viscosité :
- .
L'hypothèse de Stokes est vraie pour les gaz monoatomiques. Elle constitue une bonne approximation pour des fluides simples comme l'eau et l'air[9].
A contrario, de nombreux fluides complexes, tels que les polymères, les hydrocarbures lourds, le miel, ou encore la pâte de dentifrice, ne vérifient pas l'hypothèse du fluide newtonien. On recourt alors à d'autres lois de comportement visqueux, dites non newtoniennes (par exemple la loi du fluide de Bingham). La science qui étudie les relations entre contrainte et déformation pour de tels fluides est la rhéologie.
Propriétés thermodynamiques[modifier | modifier le code]
Le système décrit ci-dessus est incomplet puisqu'il comporte 3 équations (dont une vectorielle) pour 5 inconnues (dont deux vectorielles) : (si l'on néglige le flux de chaleur dû au rayonnement, ). On ajoute pour fermer le système des équations d'état de la forme
où T représente la température thermodynamique ; par exemple la loi des gaz parfaits :
où R désigne la constante des gaz parfaits et M la masse molaire du fluide.
Le système est alors fermé si l'on suppose vérifiée la loi de Fourier :
où λ désigne la conductivité thermique.
Propriétés de transport[modifier | modifier le code]
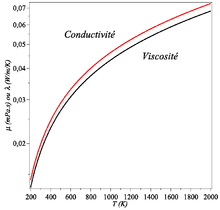

Gaz[modifier | modifier le code]
Les propriétés de transport, viscosité et conductivité, résultent d'une distribution hors d'équilibre thermodynamique dans le milieu (ne satisfaisant pas la statistique de Maxwell-Boltzmann). On sait les exprimer en utilisant la méthode de Chapman-Enskog[9].
La viscosité s'exprime sous la forme suivante :
où f (T) est une fonction lentement variable avec T, découlant du potentiel d'interaction moléculaire. La viscosité d'un gaz varie donc approximativement comme √T. Elle est indépendante de la pression.
La conductivité est étroitement liée à la viscosité :
pour un gaz monoatomique pour un gaz polyatomique
où est la capacité thermique massique à volume constant.
Dans cette expression χ = 1 correspond à la corrélation d'Eucken. La valeur exacte est plus proche de 1,3 en moyenne. Des calculs d'échanges au cours des collisions moléculaires permettent de préciser cette valeur, dépendante du gaz considéré et faiblement de la température.
Un mélange de gaz parfaits peut être traité comme un gaz unique en utilisant une approximation analytique (par exemple la loi de Sutherland) ou numérique du résultat du calcul des propriétés de ce mélange, qu'il s'agisse de la viscosité ou de la conductivité[10].
Liquides[modifier | modifier le code]
La connaissance théorique pour les liquides est beaucoup moins avancée que pour les gaz et les prédictions dans ce domaine qualitatives : la viscosité diminue avec la température[9],[11]. La connaissance des valeurs repose sur les mesures.
La variation de la conductivité avec la température ne présente pas de tendance marquée[12],[13].
Restrictions à des cas plus simples[modifier | modifier le code]
Fluides incompressibles homogènes à viscosité constante[modifier | modifier le code]
L'écoulement d'un fluide est dit incompressible et homogène lorsque l'on peut négliger ses variations de masse volumique. Cette hypothèse est vérifiée pour l'eau liquide à température fixe et les métaux en fusion. Elle est aussi vérifiée pour les gaz lorsque le nombre de Mach est faible. En général, on considère l'écoulement incompressible lorsque . De plus ce type de problème se rencontre dans des situations où la variation de température dans le milieu est faible et où l'on peut donc considérer la viscosité constante. Ceci est particulièrement vrai dans des liquides comme l'eau (voir courbe ci-dessus). De ce fait l'équation de l'énergie est découplée des équations de continuité et de quantité de mouvement, c'est-à-dire qu'on peut déterminer la vitesse et la pression indépendamment de l'équation de l'énergie. L'expression des équations de continuité et de quantité de mouvement sont considérablement simplifiées. On obtient alors
- Équation d'incompressibilité (se confondant avec l'équation de bilan de la masse pour un fluide homogène) :
- .
- Équation de bilan de la quantité de mouvement :
- où ν = μρ désigne la viscosité cinématique du fluide (unité SI : m2 s−1).
- Le membre de gauche reflète l’accélération des particules du fluide.
Cette forme plus simple des équations de Navier-Stokes pour un milieu incompressible permet d'obtenir des solutions analytiques dans quelques cas :
- dans un tube cylindrique avec une différence de pression entre l'entrée et la sortie (écoulement de Poiseuille) ;
- dans un milieu semi-infini limité par un plan se déplaçant parallèlement à lui-même (problème de Rayleigh) ;
- entre deux plans dont l'un est en mouvement permanent par rapport à l'autre (écoulement de Couette) ;
- le jet de Landau-Squire, un exemple d'écoulement auto-similaire ;
- les écoulements potentiels en point d'arrêt comme l'écoulement de Hiemenz ;
- le tourbillon de Taylor-Green utilisé pour les benchmarks de méthodes de résolution numérique ;
- le tourbillon de Lamb-Oseen.
Il existe quelques autres exemples de solutions analytiques[14],[15],[16],[17].
En utilisant l'expression des opérateurs dans les divers systèmes courants de coordonnées il est possible de détailler les expressions.
Expression en coordonnées cartésiennes
Expression en coordonnées cylindriques
Expression en coordonnées sphériques
Sous certaines hypothèses, on peut simplifier ces équations :
- en négligeant le terme inertiel du cas général (qui est égal à dans le cas incompressible), ce qui conduit à l'équation de Stokes,
- en utilisant une approximation de ce terme, ce qui conduit aux équations de Stokes-Oseen.
D’autre part, une expression de la pression peut être obtenue en prenant la divergence de l'équation de quantité de mouvement et en tenant compte de la relation d'incompressibilité :
- .
Écoulements irrotationnels[modifier | modifier le code]
On définit le vecteur tourbillon (ou la vorticité) par :
où désigne le rotationnel de la vitesse.
On peut établir une équation de conservation pour cette quantité qui est l'équation de Helmholtz.
En partant de l'équation de quantité de mouvement du chapitre précédent avec l’hypothèse de Stokes, les identités vectorielles
permettent d’obtenir la forme suivante :
- .
Supposons que le vecteur tourbillon est nul. Dans ce cas[b] :
- .
Dans ce cas toujours, puisque la vitesse est un champ irrotationnel, on peut déduire qu'elle dérive d'un potentiel que l'on note ψ :
- .
En particulier dans le cas incompressible, si on reporte cette expression dans l'équation d'incompressibilité, le potentiel obéit à l'équation de Laplace :
- .
Si, de plus, le fluide est homogène et que la force dérive d'un potentiel, par exemple la gravité, alors la propriété d'irrotationalité est automatiquement propagée en temps grâce à l'équation vérifiée par la vitesse.
Ces écoulements potentiels concernent les écoulements à faibles vitesses et peu visqueux : une voile de bateau ou une aile de planeur par exemple.
Analyse dimensionnelle[modifier | modifier le code]
Équations adimensionnelles[modifier | modifier le code]
Les équations de Navier-Stokes font intervenir 9 quantités , et 4 dimensions : temps, espace, masse, température. Le théorème de Vaschy-Buckingham montre donc l'existence de 5 variables adimensionnelles permettant l'analyse du système. Ces variables sont par exemple les nombres de Mach, Reynolds, Prandtl, Froude et Goulard. Il existe d'autres variables comme les nombres de Knudsen, de Strouhal, de Péclet ou beaucoup d'autres, mais celles-ci ne sont pas indépendantes. Les nombres de Mach, Reynolds et Knudsen par exemple sont liés entre eux, de même que les nombres de Péclet, Prandtl et Reynolds. Pour écrire ces nombres il faut définir des quantités de référence qui sont caractéristiques du problème étudié. Définissons les variables suivantes servant de références :
- une longueur L*, par exemple la taille du domaine ouvert dans un problème de milieu poreux ou de microfluidique ou le rayon de courbure de paroi en aérodynamique,
- une vitesse V*, une masse volumique ρ* et une température T*, par exemple les valeurs en amont (condition aux limites), d'où on déduit une pression ,
- une seconde vitesse a* pour la propagation des ondes sonores, par exemple pour un gaz parfait,
- une énergie interne e*, par exemple pour un gaz parfait,
- une viscosité μ* et une conductivité λ* éventuellement liée à μ* (voir propriétés de transport),
- une accélération g*,
- un flux radiatif qR*.
On peut alors définir pour ce problème les variables réduites suivantes :
| - espace | - temps | - masse volumique | - pression | ||||||||
| - viscosité | - énergie interne | - flux radiatif | - conductivité | ||||||||
| - vitesse |
et les variables adimensionnelles :
| - le nombre de Mach | |
| - le nombre de Reynolds | |
| - le nombre de Prandtl | |
| - le nombre de Froude | |
| - le nombre de Goulard |
Le système d'équations en valeurs réduites s'écrit comme suit.
- Conservation de la masse :
- où est l'opérateur nabla adimensionné utilisé dans le système de coordonnées transformé.
- Conservation de la quantité de mouvement :
- .
- Conservation de l'énergie :
- avec
- .
- Dans le cas d'un gaz parfait :
- .
Cette approche est utilisable pour l'analyse des équations et la réalisation d'expériences jugées réalistes parce que respectant le critère d'analogie en termes de nombres adimensionnels. On peut aller au-delà en utilisant une technique de la physique mathématique nommée analyse asymptotique, formalisée par David Hilbert. Dans cette méthode on développe la solution en série d'un « petit paramètre » et on analyse les approximations aux divers ordres du développement. Un exemple en est le développement en nombre de Mach montré ci-dessous. Un autre exemple très connu est le développement en nombre de Reynolds utilisé pour la couche limite.
Écoulements à faible nombre de Mach[modifier | modifier le code]
Cette approche est utilisée dans les problèmes de combustion dans lesquels les vitesses sont faibles.
Les quantités manipulées sont supposées régulières. Le développement asymptotique commence par le choix du « petit paramètre » avec lequel chacune des variables est développée. Ici ce paramètre est [c],[18],[19] :
où α représente chacune des valeurs . On regroupe les termes correspondants au même ordre du développement. Ceux-ci sont égaux puisque les équations sont vraies pour toute valeur de ε.
Par la suite on suppose valide l'hypothèse du gaz parfait.
- à l'ordre -1
- Un seul terme en ε −1 apparaît, et cela dans l'équation de quantité de mouvement :
- à l'ordre 0
- Équation de continuité
- Équation de quantité de mouvement :
- avec
- Pour la conservation de l'énergie, compte tenu de
- on obtient :
Si l'on s'arrête à l'ordre 0, après retour aux quantités dimensionnées on obtient les équations suivantes :
L'équation d'état est écrite en utilisant l'ordre 0 de la pression, l'ordre 1 (« pression dynamique ») étant une quantité en donc négligeable. Ceci a pour effet de supprimer le couplage entre masse volumique et ondes de pression.
On remarque que l'on a un système de 4 équations (dont une vectorielle) avec l'équation d'état pour 5 inconnues (dont une vectorielle) : et p1. On ferme le système avec une équation concernant la pression (qui est constante en espace).
- Dans un système ouvert la condition aux limites impose la pression p = p0 (par exemple la pression atmosphérique pour un feu à l'air libre).
- Dans un système fermé, la masse totale reste constante au cours du temps. En intégrant sur le volume du système, cela donne :
- .
Lorsque l'équation d'état du gaz parfait est utilisable, l'expression précédente devient :
- .
Remarques
- À l'ordre 0, n'intervient pas dans le bilan d'énergie.
- À cet ordre le rayonnement n'apparaît pas non plus, alors qu'il peut être un élément important du problème (en combustion par exemple). Ceci est dû au choix du nombre adimensionnel de Goulard, adapté aux écoulements à grande vitesse où l'énergie cinétique est grande devant l'énergie interne. Ici c'est le contraire et le bon nombre adimensionnel est qui est l'inverse du nombre de Boltzmann[20]. Le développement utilisant cette quantité conduit au terme dans l'équation de l'énergie et donc permet au rayonnement d'apparaître à l'ordre 0.
Couche limite[modifier | modifier le code]
Les effets des propriétés de transport, en particulier la viscosité, sont généralement limités à une mince couche au voisinage de la paroi. Il a été très tôt recherché une méthode permettant de séparer l'espace entre cette région, appelée « couche limite », et l'extérieur de celle-ci, régi par les équations d'Euler. Cette démarche, initialement introduite par Ludwig Prandtl[21] dans un cadre bidimensionnel plan a par la suite été étendue à diverses situations.
Bien que la démarche ait perdu son intérêt pratique avec les progrès en mécanique des fluides numérique (son calcul ne pose pas de difficulté numérique pour le calcul de l'écoulement dans son ensemble), elle reste un outil incontournable pour l'analyse physique[17].
Dans ce qui suit, on se limite au problème d'un écoulement incompressible stationnaire sur plaque plane (donc un écoulement plan) en négligeant les forces extérieures et le rayonnement. On reprend les équations adimensionnées ci-dessus avec , les quantités de référence étant prises dans le milieu amont. On note . Les équations de conservation s'écrivent (on fait disparaître les tildes pour alléger les notations) :
Les conditions aux limites sont :
Développements[modifier | modifier le code]
La couche limite est obtenue en utilisant le nombre de Reynolds comme facteur d'échelle du problème. Pour cela, on utilise l'analyse asymptotique simultanément pour la couche limite (milieu interne) et le milieu eulérien (milieu externe). Cette méthode est appelée méthode des développements asymptotiques raccordés. Historiquement elle est la première utilisée pour résoudre mathématiquement ce problème. D'autres méthodes sont utilisables[22].
On introduit un « petit paramètre » pour le milieu interne, pour lequel on utilise des lettres minuscules (l'expression choisie pour ce paramètre est justifiée dans la démonstration) et l'on pose . La fonction de jauge pour les développements du milieu externe (lettres majuscules) est . Elle sera choisie plus loin. Les développements s'écrivent :
| Milieu interne | Milieu externe |
|---|---|
L'équation de continuité s'applique à chaque niveau d'approximation et sera donc omise.
En utilisant les développements on obtient :
- dans la région externe
- dans la région interne
Le terme visqueux lié au cisaillement est , que l'on souhaite d'ordre 1, d'où le choix du petit paramètre
Le regroupement des termes donne :
| Ordre | Milieu interne | Milieu externe |
|---|---|---|
| 1 | ||
| 2 | ||
Dans le milieu externe, on retrouve les équations d'Euler à l'ordre 1.
On peut écrire les équations internes en variables physiques adimensionnées en posant :
| Ordre 1 | Ordre 2 |
|---|---|
En y ajoutant l'équation de continuité, l'ordre 1 constitue les équations de Prandtl telles que Prandtl les a obtenues par analyse d'échelle[21],[22].
À l'ordre 2, le gradient de pression est non nul pour une paroi courbe.
Conditions aux limites : les raccordements[modifier | modifier le code]
Le raccordement se fait en choisissant la fonction de jauge , valeur issue de la comparaison des valeurs de u et v dans les deux milieux.
Le développement en série de Taylor pour u dans le milieu externe s'écrit :
Cette expression doit être comparée terme à terme avec la limite pour du développement interne :
Pour v dans le milieu externe :
Et dans le milieu interne :
L'identification impose . Les termes en , non raccordés, sont donc ignorés.
On obtient ainsi les conditions aux limites :
| Ordre 1 | Ordre 2 |
|---|---|
Au premier ordre, il y a un découplage entre les deux milieux : tout se passe comme si l'épaisseur de couche limite était nulle. Par contre, l'épaisseur de couche limite apparaît au second ordre avec la condition sur .
Généralisations[modifier | modifier le code]
De nombreux développements de la notion de couche limite ont été effectués[17] :
- pour les écoulements compressibles[23] ;
- pour les écoulements instationnaires ;
- pour les écoulements tridimensionnels[24] : au premier ordre on peut calculer cette couche pour chaque ligne de courant préalablement définie à partir de l'écoulement eulérien. La surface courbe normale au corps ainsi définie comporte une vitesse dans le plan très supérieure à la vitesse transverse. Si on néglige cette dernière le problème tridimensionnel se réduit à une série de problèmes bidimensionnels ;
- le concept a été généralisé à la triple couche (l'espace est divisé en trois régions superposées) permettant d'analyser le phénomène de décollement, ce qui est interdit par construction de la couche limite[22].
Singularités[modifier | modifier le code]
Il convient de préciser la notion de singularité : un choc est une singularité au sens mathématique des équations d'Euler mais la solution correspondante des équations de Navier-Stokes est continue. Ce problème d'apparition d'une singularité lié à une restriction des équations est un problème assez général. On peut citer par exemple la singularité de Prandtl-Glauert qui est liée à l'approximation incompressible.
Le problème général de l'apparition en temps fini dans les équations de Navier-Stokes de singularités est un problème ouvert.
Choc[modifier | modifier le code]

En écoulement supersonique et dans le cadre des équations d'Euler le choc est une discontinuité non transitoire de toutes les quantités dans l'écoulement. Son épaisseur est de quelques libres parcours moyens : sa description détaillée relève de l'équation de Boltzmann et non des équations de Navier-Stokes. Ses caractéristiques sont décrites par les relations de Rankine-Hugoniot qui donnent le rapport des valeurs avant et après le choc. L'existence d'une telle discontinuité est liée à la nature hyperbolique des équations d'Euler.
Le choc est un train continu d'ondes de Riemann à la différence de l'onde simple que constitue le son. Toutefois un choc peut dégénérer en une onde de Mach qui est une onde sonore, donc une discontinuité transitoire.
Ligne de glissement[modifier | modifier le code]
La ligne de glissement, encore appelée discontinuité de contact, désigne l'interface entre deux écoulements parallèles de vitesses différentes mais de même pression. Cette discontinuité respecte les relations de Rankine-Hugoniot. Elle est généralement le résultat d'interactions de chocs.
Ligne ou point d'arrêt[modifier | modifier le code]
La ligne ou le point d'arrêt désigne une ligne ou un point où la vitesse de l'écoulement s'annule lorsque l'écoulement rencontre un corps convexe. Ceci résulte de l'existence d'un ou plusieurs plans de symétrie de l'objet parallèles à l'écoulement à l'infini amont, ce qui entraîne l'échappement du fluide dans diverses directions parallèles à la tangente locale au corps (brisure spontanée de symétrie). La vitesse en ce point est nulle du fait de la symétrie et de l'équation de continuité. Le module de la vitesse à partir du point (ou de la ligne) d'arrêt est le même dans les directions symétriques.
A contrario le centre d'une implosion, à symétrie sphérique, comporte un point où les vitesses s'annulent sans provoquer une singularité, la variable position étant continument dérivable.
Autres problèmes[modifier | modifier le code]
Outre le problème précédent il existe d'autres instabilités créées par les conditions aux limites, par exemple la partition d'une goutte dans laquelle on montre l'auto-similitude de la forme[25].
Instabilités et transition vers la turbulence[modifier | modifier le code]
Instabilités[modifier | modifier le code]
Beaucoup d'écoulements homogènes présentent des instabilités. Certaines d'entre elles vont conduire à une organisation spatio-temporelle stable, périodique comme les tourbillons de Karman ou ceux de Görtler, ou stationnaire comme l'instabilité de Rayleigh-Bénard. D'autres, de nature inertielle, conduiront à la création de tourbillons (instabilité de Kelvin-Helmholtz), éventuellement suivis d'écoulements instationnaires (instabilité de Taylor-Couette).
Des instabilités secondaires pourront se créer, entraînant le milieu vers la turbulence, comme dans le cas de l'instabilité de Richtmyer-Meshkov où se crée une instabilité secondaire de type Kelvin-Helmholtz[26]. Les instabilités peuvent être compétitives comme dans le cas des toubillons de Görtler et des onde de Tollmien-Schlichting. Les mécanismes de transition laminaire-turbulent ont été particulièrement étudiés dans le cas de la couche limite et montrent la diversité des mécanismes en jeu. Leur étude est très liée à l'étude des systèmes dynamiques [27].
Turbulence[modifier | modifier le code]
Le stade final de l'écoulement peut être celui d'un système pleinement turbulent, tel que défini par la cascade turbulente, comportant des échelles très différentes, de l'échelle de Kolmogorov à l'échelle intégrale, ce qui rend la description numérique très coûteuse. Elle est effectuée dans des cas académiques dans le but de comprendre les phénomènes qui seront ensuite décrits à plus grande échelle qui utilisent des modèles décrivant la part du phénomène non accessible au calcul numérique.
Conditions aux limites[modifier | modifier le code]
Conditions entrantes et sortantes[modifier | modifier le code]
Il n'y a pas, sauf exception, de conditions entrantes ou sortantes spécifiques au système de Navier-Stokes. En effet les effets visqueux sont généralement confinés en des endroits spécifiques connus à l'avance. Le domaine de calcul inclut donc ces régions et on est ainsi ramené au problème des conditions entrantes et sortantes pour les équations d'Euler. On peut ajouter que donner des conditions dans une région où les effets visqueux sont importants constitue une tâche des plus ardues.
Conditions pariétales[modifier | modifier le code]
Il n'est pas possible stricto sensu d'écrire des telles conditions aux limites. En effet, comme le montre la méthode de Chapman-Enskog dans le cas des gaz, le système de Navier-Stokes suppose au niveau microscopique une faible perturbation de la distribution de Maxwell-Boltzmann. Cette hypothèse est invalide au voisinage d'une paroi, laquelle perturbe fortement la distribution des vitesses et des énergies internes des molécules. La résolution de la région perturbée ou couche de Knudsen montre l'existence de sauts de vitesse et de température qui sont d'autant plus faibles que la pression augmente. Si celle-ci est suffisante on peut négliger des discontinuités et les conditions pariétales se réduisent alors aux conditions généralement données sans justification[d] :
- à la paroi (condition d'adhérence),
- T = Tp à la paroi, où Tp est la température de paroi, donnée.
Dans le cas d'un échange pariétal (injection, succion) les conditions aux limites s'écrivent en utilisant la conservation des flux de masse, quantité de mouvement et énergie au travers de la surface. Dans le cas particulier de flux nuls on trouve les conditions :
- à la paroi, où est le vecteur unitaire normal à la surface ;
- T = T0, où T0 est la température d'interface.
La composante tangentielle de la vitesse est spécifique au problème traité.
Les problèmes de paroi rugueuse dans un écoulement turbulent peuvent être traités en utilisant une loi de paroi utilisant une rugosité « grain de sable » apparente permettant d'exploiter la loi classique de von Kármán. Des méthodes plus élaborées de décomposition de domaine traitent numériquement ce problème en écoulement laminaire, plus difficilement en écoulement turbulent.
Domaines d'utilisation[modifier | modifier le code]
-
Calcul d'aérodynamique supersonique en variables eulériennes. -
Calcul d'un jet astrophysique en variables lagrangiennes. -
Simulation d'un feu de kérosène dans un bâtiment. -
Vagues côtières. -
Simulation d'un ouragan. -
Écoulement ventriculaire.
Les domaines d'utilisation sont exceptionnellement larges[28] :
- aérodynamique externe : avion, planeur, missile, lanceur, sonde spatiale, automobile, vol des insectes, bâtiments et ponts ;
- aérodynamique interne : moteurs d'avion, turbines à gaz, moteurs-fusées, climatisation ;
- hydrodynamique : bateau, sous-marin, propulsion marine ;
- hydraulique : canalisations, canaux ouverts, vagues, rivières, circulation sanguine ;
- metéodynamique : météorologie, climatologie ;
- astrophysique : formation des étoiles, des systèmes stellaires, des galaxies, de l'univers, des jets stellaires ;
- armement : explosions ;
- sécurité : feux de nappes, feux de forêt et feux confinés ;
Popularisation[modifier | modifier le code]
Les équations de Navier-Stokes pour un fluide incompressible font partie des problèmes du prix du millénaire de l'institut de mathématiques Clay. La résolution de ces équations, le cas échéant, sera récompensée d'un prix d'un million de dollars[29].
Les équations de Navier-Stokes sont le principal sujet du film Mary de Marc Webb, sorti en 2017.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Les équations de Navier-Stokes adoptent l’approximation des milieux continus, approximation qui est acceptable pour la plupart des fluides, à l'exception des gaz extrêmement raréfiés.
- Le terme Ω × V peut également être nul si Ω et V sont parallèles. Cette condition décrit les écoulements de Beltrami.
- On peut également effectuer un développement en qui permet de prendre en compte les ondes acoustiques.
- Ces conditions peuvent être plus complexes lorsqu'il existe une interaction physico-chimique gaz-paroi. On écrit alors des équations de conservation des flux.
Références[modifier | modifier le code]
- .
- (en) George Gabriel Stokes, Transactions of Cambridge Philosophical Society, vol. 8, 1845, p. 287–305.
- Isabelle Gallagher, « Autour des équations de Navier-Stokes », sur images.math.cnrs.fr, (consulté le ).
- Augustin Louis Cauchy, « Sur l’équilibre et le mouvement des liquides et des fluides élastiques », Mémoire de l'Académie royale des sciences, t. 11, , p. 413-418 (lire en ligne), sur Gallica.
- Siméon Denis Poisson, « Mémoire sur les équations générales de l'équilibre et du mouvement des corps solides élastiques et des fluides », lu à l'Académie royale des sciences le 12 octobre 1829 avant publication au 20e cahier du Journal de l'École polytechnique, Imprimerie royale, 1830, t. 13, p. 394-412.
- (en) V. Giovangigli, « Multicomponent Flow », sur Scholarpedia, « Transport coefficients ».
- ISO/CEI 80000-2:2009 Grandeurs et unités — Partie 2: signes et symboles mathématiques à employer dans les sciences de la nature et dans la technique.
- Pierre-Louis Lions, Mathematical topics in fluid mechanics, Vol. 1 : incompressible models, Clarendon Press, , 252 p. (ISBN 978-0-19-851487-9, OCLC 34517004, lire en ligne).
- (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, (ISBN 978-0-471-40065-3).
- (en) Duffa G., Ablative Thermal Protection Systems Modeling, Reston, VA, AIAA Educational Series, , 431 p. (ISBN 978-1-62410-171-7).
- (en) Yeram Sarkis Touloukian, S.C. Saxena et P. Hestermans, Viscosity, New York, IFI/Plenum, coll. « Thermophysical properties of matter » (no 11), , 643 p. (ISBN 978-0-306-67031-2 et 978-0-306-67020-6, OCLC 2296975, lire en ligne).
- (en) Yeram Sarkis Touloukian, P. E. Liley, S. C. Saxena, Thermal Conductivity. Nonmetallic Liquids and Gases, Rapport TPRC Data Series, Vol. 3, Information for Industry, Inc. (IFI)/Plenum Press, 1970 (SBN 306-67023-2) [1]
- (en) Yeram Sarkis Touloukian, R. W. Powell, C. Y. Ho, M. C. Nicolaou, Thermal Diffusivity, Rapport TPRC Data Series, Vol. 10, Information for Industry, Inc. (IFI)/Plenum Press, 1973 [2]
- (en) Ronald L. Panton, Incompressible Flow, Wiley, (lire en ligne)
- (en) Philip Drazin and Norman Riley, The Navier-Stokes Equations. A Classification of Flows and Exact Solutions., London Mathematical Society. Lecture Notes Series 334, Cambridge University Press, 2006 (ISBN 0-521-68162-6).
- A. Rosenblatt, « Solutions exactes des équations du mouvement des liquides visqueux », Mémorial des sciences mathématiques, (lire en ligne).
- (en) Hermann Schlichting, Boundary Layer Theory, McGraw Hill, (ISBN 3662570955, lire en ligne [PDF]).
- (en) B. Müller, Low Mach Number Asymptotics of the Navier-Stokes Equations and Numerical Implications, Von Karman Institute for Fluid Dynamics, Lecture Series 1999-03, March 1999.
- (en) Radyadour Kh. Zeytounian, Asymptotic Modelling of Fluid Flow Phenomena, Kluwer Academic Publishers, , 550 p. (ISBN 0-306-48386-6, lire en ligne).
- Stanford S. Penner et Daniel B. Olfe, Radiation and reentry, Academic Press,
- (en) John D. Anderson Jr., « Ludwig Prandtl's Boundary Layer » [PDF], sur Physics Today, .
- Jean Cousteix et Jacques Mauss, Analyse asymptotique et couche limite, Springer, (ISBN 3-540-31002-9).
- Jean-Philippe Brazier, Étude asymptotique des équations de couche limite en formulation déficitaire, Thèse de l'ENSAE, (lire en ligne)
- (en) Ernst Heinrich Hirschel, Jean Cousteix et Wilhelm Kordulla, Three-Dimensional Attached Viscous Flow, Springer, (ISBN 978-3-642-41377-3)
- (en) Andrea L. Bertozzi, Michael P. Brenner, Todd F. Dupont et Leo P. Kadanoff, Singularities and Similarities in Interface Flows, Springer, coll. « Trends and Perspectives in Applied Mathematics » (ISBN 978-1-4612-6924-3, lire en ligne), p. 155–208
- (en) O. A. Azarova, « Generation of Richtmyer–Meshkov and secondary instabilities during the interaction of an energy release with a cylinder shock layer », Aerospace Science and Technology, vol. 42, , p. 376-383
- (en) Paul Manneville, Instabilités, Chaos and Turbulence : An Introduction to Nonlinear Dynamics and Complex Systems,, Imperial College Press, (ISBN 1-86094-483-3, lire en ligne)
- (en) R. Yountsi Ed., Navier-Stokes Equations: Properties, Description and Applications, Nova Science Publishers, (ISBN 978-1-61324-590-3).
- Rachel Crowell, « Vingt et un ans après, les problèmes mathématiques « du millénaire » restent mystérieux », Pour la Science, (lire en ligne, consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Sébastien Candel, Mécanique des fluides : cours, Paris, Dunod, Paris, , 451 p. (ISBN 2-10-005372-8)
- James Luneau et Allan Bonnet, Aérodynamique théories de la dynamique des fluides, Toulouse, Éditions Cépaduès, coll. « Sup'Aero », , 544 p. (ISBN 978-2-85428-218-4 et 2854282183).
- Etienne Guyon, Jean-Pierre Hulin et Luc Petit (préf. John Hinch), Hydrodynamique physique, Les Ulis/Paris, EDP Sciences/CNRS Éditions, coll. « Savoirs actuels », , 3e éd., 689 p. (ISBN 978-2-7598-0561-7 et 2759805611).
- (en) Lev Davidovitch Landau et Evgueni Mikhaïlovitch Lifshitz, Volume 6 of Course of Theoretical Physics : Fluid Mechanics, Pergamon Press,
- (en) Brian J. Cantwell, Fundamentals of Compressible Flows, Cours de l'université de Stanford [3]
- (en) Sandra Cerrai et Nikolas Paskal, « Large deviations principle for the invariant measures of the 2D stochastic Navier–Stokes equations with vanishing noise correlation », Stochastics and Partial Differential Equations: Analysis and Computations, Springer Science+Business Media, vol. 10, , p. 1651–1681 (DOI 10.1007/s40072-021-00219-5).
Articles connexes[modifier | modifier le code]
- Dynamique des fluides
- Aérodynamique
- Mécanique des fluides numérique
- Équation de Navier
- Équations de Saint-Venant
- Équation de Burgers
- Équation d'Hugoniot
- Approximation de Boussinesq
- Équation de Taylor-Goldstein
- Relations de Rankine-Hugoniot
- Écoulement de Stokes
- Équations de Stokes-Oseen
- Détente de Prandtl-Meyer
- Équation de Orr-Sommerfeld
- Théorème de Crocco
- Approximation de lubrification
- Effet Coandă
- Ondes de Tollmien-Schlichting
- Tourbillons de Görtler
- Projecteur de Leray
- Équations fondamentales de la mécanique des milieux continus














![{\displaystyle {\begin{array}{rcl}{\vec {\nabla }}\times ({\vec {\nabla }}\,\phi )&=&0\\[0.2em]{\vec {\nabla }}\cdot ({\vec {\nabla }}\times {\vec {A}})&=&0\\[0.2em]({\vec {\nabla }}\times {\vec {A}})\times {\vec {A}}&=&({\vec {A}}\cdot {\vec {\nabla }})\,{\vec {A}}-{\vec {\nabla }}A\,{\vec {A}}\\[0.2em]{\vec {\nabla }}A\,{\vec {A}}&=&{\frac {1}{2}}\,{\vec {\nabla }}\,({\vec {A}}\cdot {\vec {A}})\\[0.2em]{\vec {\nabla }}\cdot ({\vec {\nabla }}\phi )&=&{\vec {\nabla }}^{2}\phi \\[0.2em]{\vec {\nabla }}\times ({\vec {\nabla }}\times {\vec {A}})&=&{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {A}})-\Delta {\vec {A}}\\[0.2em]{\vec {\nabla }}\cdot (\alpha \,{\mathsf {T}}\,)&=&{\vec {\nabla }}\alpha \cdot {\mathsf {T}}\,+({\vec {\nabla }}\cdot {\mathsf {T}}\,)\,\alpha \\[0.2em]{\vec {\nabla }}\cdot ({\vec {A}}{\vec {B}})&=&({\vec {B}}\cdot {\vec {\nabla }})\,{\vec {A}}+{\vec {A}}\,({\vec {\nabla }}\cdot {\vec {B}})\\[0.2em]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0ecc0ad4d3119bee8681bc6dbfd805c42841db2)





![{\displaystyle {\begin{array}{rcl}{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)&=&{\vec {\nabla }}\cdot {\mathsf {P}}+\rho {\vec {g}}\\[0.5em]&=&-{\vec {\nabla }}p+{\vec {\nabla }}\cdot {\mathsf {\Sigma }}+\rho {\vec {g}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/750a016d081aa71edb4847e2d8cbae0990de5c18)









![{\displaystyle {\frac {\partial \left(\rho {\vec {V}}\right)}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)=\rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db299ee655ee4eed2d1d676060d895a7dbd2332)
![{\displaystyle {\begin{array}{rcll}{\frac {\partial \left(\rho {\vec {V}}\right)}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)&=&{\vec {V}}\,{\frac {\partial \rho }{\partial t}}+\rho \,{\frac {\partial {\vec {V}}}{\partial t}}+{\vec {V}}({\vec {V}}\cdot {\vec {\nabla }}\rho )+\rho ({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}+\rho {\vec {V}}\,({\vec {\nabla }}\cdot {\vec {V}})&{\text{Développement}}\\[0.5em]&=&\rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}\right]+{\vec {V}}\left[{\frac {\partial \rho }{\partial t}}+{\vec {V}}\cdot {\vec {\nabla }}\rho +\rho {\vec {\nabla }}\cdot {\vec {V}}\right]&{\text{Regroupement des termes}}\\[0.5em]&=&\rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}\right]+{\vec {V}}{\cancelto {0}{\left[{\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot (\rho {\vec {V}})\right]}}&{\text{Simplification}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa1f1487b641105683facac13e60db549362e73)

![{\displaystyle {\frac {\partial (\rho E)}{\partial t}}+{\vec {\nabla }}\cdot [(\rho E+p){\vec {V}}]={\vec {\nabla }}\cdot \left({\mathsf {\Sigma }}\cdot {\vec {V}}\right)+\rho {\vec {g}}\cdot {\vec {V}}+{\vec {\nabla }}\cdot {\vec {q}}+{\vec {q}}_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a118e471d8b1fe9e99955e87f2e97315436caa4)

![{\displaystyle \rho \left[{\frac {\partial }{\partial t}}\left({\frac {\|{\vec {V}}\|^{2}}{2}}\right)+{\vec {V}}\cdot {\vec {\nabla }}\left({\frac {\|{\vec {V}}\|^{2}}{2}}\right)\right]=({\vec {\nabla }}\cdot {\mathsf {P}})\cdot {\vec {V}}+\rho {\vec {g}}\cdot {\vec {V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eee1be6a5a7dcbd23423d178aec54823d2567d91)



![{\displaystyle {\begin{array}{rcl}{\dfrac {\mathrm {D} (\rho {\vec {V}})}{\mathrm {D} t}}=\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{\xi }&=&\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{x}+\left({\vec {V}}\cdot {\vec {\nabla }}\right)(\rho {\vec {V}})\\[0.8em]&=&\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{x}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)-\rho \left({\vec {\nabla }}\cdot {\vec {V}}\right){\vec {V}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d40748a57f3cc2a2e3ae8b6fb6abb20ca12f36c0)




![{\displaystyle {\begin{array}{rcl}{\frac {\partial \rho }{\partial t}}+\sum _{i=1}^{3}{\frac {\partial }{\partial x_{i}}}(\rho V_{i})&=&0\\[0.5em]{\frac {\partial \left(\rho V_{j}\right)}{\partial t}}+\sum _{i=1}^{3}{\frac {\partial }{\partial x_{i}}}\left(\rho V_{i}V_{j}\right)&=&-{\frac {\partial p}{\partial x_{j}}}+\sum _{i=1}^{3}{\frac {\partial \sigma _{ij}}{\partial x_{i}}}+\rho f_{j}\\[0.5em]{\frac {\partial \left(\rho e\right)}{\partial t}}+\sum _{i=1}^{3}{\frac {\partial }{\partial x_{i}}}\left[\left(\rho e+p\right)V_{i}\right]&=&\sum _{i=1}^{3}\sum _{j=1}^{3}{\frac {\partial }{\partial x_{i}}}\left(\sigma _{ij}V_{j}\right)+\sum _{i=1}^{3}\rho f_{i}V_{i}-\sum _{i=1}^{3}{\frac {\partial {\dot {q}}_{i}}{\partial x_{i}}}+r\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d01a23c999874bc5502e29e6486d69e265ad840)








![{\displaystyle {\mathsf {\Sigma }}=\mu \left[\,{\vec {\nabla }}{\vec {V}}+({\vec {\nabla }}{\vec {V}}\,)^{T}\right]+\mu '({\vec {\nabla }}\cdot {\vec {V}}\,)\;{\mathsf {I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ce3caaed1716721ee89131a3f3a4e84d8c3ff1)
![{\displaystyle \rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+\left({\vec {V}}\cdot {\vec {\nabla }}\right){\vec {V}}\right]=-{\vec {\nabla }}p+{\vec {\nabla }}\cdot \left\{\mu \left[{\vec {\nabla }}{\vec {V}}+({\vec {\nabla }}{\vec {V}}\,)^{T}\right]+\mu '({\vec {\nabla }}\cdot {\vec {V}})\,{\mathsf {I}}\,\right\}+\rho \,{\vec {g}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f466b5dfbd283e51fa24039b62f0008efe10b28)



![{\displaystyle \rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+\left({\vec {V}}\cdot {\vec {\nabla }}\right){\vec {V}}\right]=-{\vec {\nabla }}p+\mu \,\nabla ^{2}{\vec {V}}+(\mu +\mu ')\,{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})+\rho \,{\vec {g}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a66cea2aeb9ab48544c2ab9ba46643680c01584)






![{\displaystyle {\frac {\lambda }{\mu }}=\left\{{\begin{array}{lcr}{\frac {5}{2}}C_{\mathcal {V}}\\[0.5em]C_{\mathcal {V}}+{\frac {15-6\chi }{4}}R\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99cd33cad4447c2ebffa376dae846214b8409772)





![{\displaystyle {\begin{array}{rcl}{\partial V_{x} \over \partial x}+{\partial V_{y} \over \partial y}+{\partial V_{z} \over \partial z}&=&0\\[0.5em]{\frac {\partial V_{x}}{\partial t}}+V_{x}{\frac {\partial V_{x}}{\partial x}}+V_{y}{\frac {\partial V_{x}}{\partial y}}+V_{z}{\frac {\partial V_{x}}{\partial z}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}}+\nu \left({\frac {\partial ^{2}V_{x}}{\partial x^{2}}}+{\frac {\partial ^{2}V_{x}}{\partial y^{2}}}+{\frac {\partial ^{2}V_{x}}{\partial z^{2}}}\right)+f_{x}\\[0.5em]{\frac {\partial V_{y}}{\partial t}}+V_{x}{\frac {\partial V_{y}}{\partial x}}+V_{y}{\frac {\partial V_{y}}{\partial y}}+V_{z}{\frac {\partial V_{y}}{\partial z}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial y}}+\nu \left({\frac {\partial ^{2}V_{y}}{\partial x^{2}}}+{\frac {\partial ^{2}V_{y}}{\partial y^{2}}}+{\frac {\partial ^{2}V_{y}}{\partial z^{2}}}\right)+f_{y}\\[0.5em]{\frac {\partial V_{z}}{\partial t}}+V_{x}{\frac {\partial V_{z}}{\partial x}}+V_{y}{\frac {\partial V_{z}}{\partial y}}+V_{z}{\frac {\partial V_{z}}{\partial z}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+\nu \left({\frac {\partial ^{2}V_{z}}{\partial x^{2}}}+{\frac {\partial ^{2}V_{z}}{\partial y^{2}}}+{\frac {\partial ^{2}V_{z}}{\partial z^{2}}}\right)+f_{z}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d5479e07f4ff8db8ee445e502910d25f9662b4c)
![{\displaystyle {\begin{array}{rcl}{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rV_{r}\right)+{\frac {1}{r}}{\frac {\partial V_{\phi }}{\partial \phi }}+{\frac {\partial V_{z}}{\partial z}}&=&0\\[0.5em]{\frac {\partial V_{r}}{\partial t}}+V_{r}{\frac {\partial V_{r}}{\partial r}}+{\frac {V_{\phi }}{r}}{\frac {\partial V_{r}}{\partial \phi }}+V_{z}{\frac {\partial V_{r}}{\partial z}}-{\frac {V_{\phi }^{2}}{r}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}+\nu \left[{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial V_{r}}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}V_{r}}{\partial \phi ^{2}}}+{\frac {\partial ^{2}V_{r}}{\partial z^{2}}}-{\frac {V_{r}}{r^{2}}}-{\frac {2}{r^{2}}}{\frac {\partial V_{\phi }}{\partial \phi }}\right]+f_{r}\\[0.5em]{\frac {\partial V_{\phi }}{\partial t}}+V_{r}{\frac {\partial V_{\phi }}{\partial r}}+{\frac {V_{\phi }}{r}}{\frac {\partial V_{\phi }}{\partial \phi }}+V_{z}{\frac {\partial V_{\phi }}{\partial z}}+{\frac {V_{r}V_{\phi }}{r}}&=&-{\frac {1}{\rho r}}{\frac {\partial p}{\partial \phi }}+\nu \left[{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial V_{\phi }}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}V_{\phi }}{\partial \phi ^{2}}}+{\frac {\partial ^{2}V_{\phi }}{\partial z^{2}}}+{\frac {2}{r^{2}}}{\frac {\partial V_{r}}{\partial \phi }}-{\frac {V_{\phi }}{r^{2}}}\right]+f_{\phi }\\[0.5em]{\frac {\partial V_{z}}{\partial t}}+V_{r}{\frac {\partial V_{z}}{\partial r}}+{\frac {V_{\phi }}{r}}{\frac {\partial V_{z}}{\partial \phi }}+V_{z}{\frac {\partial V_{z}}{\partial z}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+\nu \left[{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial V_{z}}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}V_{z}}{\partial \phi ^{2}}}+{\frac {\partial ^{2}V_{z}}{\partial z^{2}}}\right]+f_{z}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb00159fa874118d90a4731f4868f63fbe749066)
![{\displaystyle {\begin{array}{rcl}{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}V_{r}\right)+{\frac {1}{r\sin \theta }}{\frac {\partial V_{\phi }}{\partial \phi }}+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta \,V_{\theta }\right)&=&0\\[0.5em]{\frac {\partial V_{r}}{\partial t}}+V_{r}{\frac {\partial V_{r}}{\partial r}}+{\frac {V_{\phi }}{r\sin \theta }}{\frac {\partial V_{r}}{\partial \phi }}+{\frac {V_{\theta }}{r}}{\frac {\partial V_{r}}{\partial \theta }}-{\frac {V_{\phi }^{2}+V_{\theta }^{2}}{r}}&=&-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}+f_{r}+\nu \left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial V_{r}}{\partial r}}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}V_{r}}{\partial \phi ^{2}}}\right.\\[0.5em]&&\left.+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial V_{r}}{\partial \theta }}\right)-{\frac {2}{r^{2}}}\left(V_{r}+{\frac {\partial V_{\theta }}{\partial \theta }}+{\frac {V_{\theta }}{\tan \theta }}\right)-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial V_{\phi }}{\partial \phi }}\right]\\[0.5em]{\frac {\partial V_{\theta }}{\partial t}}+V_{r}{\frac {\partial V_{\theta }}{\partial r}}+{\frac {V_{\phi }}{r\sin \theta }}{\frac {\partial V_{\theta }}{\partial \phi }}+{\frac {V_{\theta }}{r}}{\frac {\partial V_{\theta }}{\partial \theta }}+{\frac {V_{r}V_{\theta }-V_{\phi }^{2}\cot \theta }{r}}&=&-{\frac {1}{\rho r}}{\frac {\partial p}{\partial \theta }}+f_{\theta }+\nu \left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial V_{\theta }}{\partial r}}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}V_{\theta }}{\partial \phi ^{2}}}\right.\\[0.5em]&&\left.+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial V_{\theta }}{\partial \theta }}\right)+{\frac {2}{r^{2}}}{\frac {\partial V_{r}}{\partial \theta }}-{\frac {1}{r^{2}\sin ^{2}\theta }}\left(V_{\theta }+2\cos \theta \,{\frac {\partial V_{\phi }}{\partial \phi }}\right)\right]\\[0.5em]{\frac {\partial V_{\phi }}{\partial t}}+V_{r}{\frac {\partial V_{\phi }}{\partial r}}+{\frac {V_{\phi }}{r\sin \theta }}{\frac {\partial V_{\phi }}{\partial \phi }}+{\frac {V_{\theta }}{r}}{\frac {\partial V_{\phi }}{\partial \theta }}+{\frac {Vu_{r}V_{\phi }+V_{\phi }V_{\theta }\cot \theta }{r}}&=&-{\frac {1}{\rho r\sin \theta }}{\frac {\partial p}{\partial \phi }}+f_{\phi }+\nu \left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial V_{\phi }}{\partial r}}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}V_{\phi }}{\partial \phi ^{2}}}\right.\\[0.5em]&&\left.+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial V_{\phi }}{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}\left(2\sin \theta {\frac {\partial V_{r}}{\partial \phi }}+2\cos \theta \,{\frac {\partial V_{\theta }}{\partial \phi }}-V_{\phi }\right)\right]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/758459ce8a239fe952c9b6c8b8edd31b77d98449)


![{\displaystyle {\vec {\nabla }}^{2}p=-\rho \,{\vec {\nabla }}\cdot [{\vec {\nabla }}\cdot ({\vec {V}}{\vec {V}})]+\rho \,{\vec {\nabla }}\cdot {\vec {g}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d267fc9ca8738be3bc1ce7b3b5ce6f744db1f850)


![{\displaystyle {\begin{array}{rcl}({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}&=&({\vec {\nabla }}\times {\vec {V}})\times {\vec {V}}+{\vec {\nabla }}V\,{\vec {V}}\\[0.5em]{\vec {\nabla }}\times ({\vec {\nabla }}\times {\vec {V}})&=&{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})-\nabla ^{2}{\vec {V}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38e5b22009f4b17ba2a8f929bbed07ce1202f4c4)

























![{\displaystyle {\tilde {\mathsf {\Sigma }}}={\tilde {\mu }}\left[{\vec {\nabla }}_{\tilde {x}}{\vec {\tilde {V}}}+({\vec {\nabla }}_{\tilde {x}}{\vec {\tilde {V}}})^{T}-{\frac {2}{3}}({\vec {\nabla }}_{\tilde {x}}\cdot {\vec {\tilde {V}}})\,{\mathsf {I}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e197edbc7b8c253eb63a6fd7cfbc170d3e2cb5ab)
![{\displaystyle {\frac {\partial ({\tilde {\rho }}{\tilde {E}})}{\partial {\tilde {t}}}}+\nabla _{\tilde {x}}\cdot \left[\left({\tilde {\rho }}{\tilde {E}}+{\tilde {p}}\right){\vec {\tilde {V}}}\right]={\frac {{\mathcal {M}}a^{2}}{{\mathcal {R}}e}}\nabla _{\tilde {x}}\cdot ({\tilde {\Sigma }}\cdot {\vec {\tilde {V}}})\,+\,{\frac {{\mathcal {M}}a^{2}}{{\mathcal {F}}r}}\,{\tilde {\rho }}\,{\vec {\tilde {g}}}\cdot {\vec {\tilde {V}}}\,-\,{\frac {1}{(\gamma ^{*}-1){\mathcal {R}}e\,{\mathcal {P}}r}}\nabla _{\tilde {x}}\cdot ({\tilde {\lambda }}\,{\tilde {\nabla }}_{\tilde {x}}\,{\tilde {T}})\,+\,{\frac {1}{2}}{\mathcal {G}}{\mathcal {M}}a^{2}\nabla _{\tilde {x}}\cdot {\vec {\tilde {q}}}_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/315de27efcc074ee486e666da09eb36b107b9dad)








![{\displaystyle {\tilde {\mathsf {\Sigma }}}^{(0)}=\mu \left[{\vec {\nabla }}_{\tilde {x}}{\tilde {\vec {V}}}^{(0)}+({\vec {\nabla }}_{\tilde {x}}{\tilde {\vec {V}}}^{(0)})^{T}-{\frac {2}{3}}({\vec {\nabla }}_{\tilde {x}}{\tilde {\vec {V}}}^{(0)})\,{\mathsf {I}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ffa5754546b1049dddb1106641db334a64c42f)

![{\displaystyle {\frac {\mathrm {d} {\tilde {p}}^{(0)}}{\mathrm {d} {\tilde {t}}}}+\left[\gamma ^{*}(\gamma ^{*}-1)^{2}\right]{\tilde {p}}^{(0)}{\vec {\nabla }}_{\tilde {x}}\cdot {\tilde {\vec {V}}}^{(0)}=-\,{\frac {\gamma ^{*}(\gamma ^{*}-1)}{{\mathcal {R}}e\,{\mathcal {P}}r}}{\vec {\nabla }}_{\tilde {x}}\cdot (\lambda \,{\vec {\nabla }}_{\tilde {x}}\,{\tilde {T}}^{(0)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dafc31fe3bd30be4107964c26c1f8bc79bea1fa)
![{\displaystyle {\begin{array}{rcl}p&=&f(t)\\[0.3em]{\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot (\rho {\vec {V}})&=&0\\[0.3em]{\frac {\partial \left(\rho {\vec {V}}\right)}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)&=&-{\vec {\nabla }}p_{1}+{\vec {\nabla }}\cdot {\mathsf {\Sigma }}+\rho {\vec {g}}\\[0.4em]{\frac {\mathrm {d} p}{\mathrm {d} t}}+p{\vec {\nabla }}\cdot {\vec {V}}&=&-{\vec {\nabla }}\cdot (\lambda \,{\vec {\nabla }}T)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edaf66ba63c7a347e7549f4b1b5287bf80f207d2)













































![{\displaystyle u=\lim \limits _{{\bar {y}}\to 0}{\left[u_{1}(x,{\bar {y}})+\epsilon u_{2}(x,{\bar {y}})\right]}=U_{1}(x,0)+\epsilon \left(U_{2}(x,0)+{\bar {y}}{\frac {\partial U_{1}}{\partial y}}(x,0)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f49502ec21dfb48f20abed74c97f543c0a8ecfe)

![{\displaystyle v=\lim \limits _{{\bar {y}}\to \infty }{\left[\epsilon {\bar {v}}_{1}(x,{\bar {y}})+\epsilon ^{2}{\bar {v}}_{2}(x,{\bar {y}})\right]}=V_{1}(x,0)+\epsilon \left[V_{2}(x,0)+{\bar {y}}{\frac {\partial V_{1}}{\partial y}}(x,0)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e831ca4c03e3db4112a334517eced1c501e80ed9)






![{\displaystyle \qquad V_{2}(x,0)=\lim \limits _{{\bar {y}}\to \infty }{\left[{\bar {v}}_{1}(x,{\bar {y}})-{\bar {y}}{\frac {\partial V_{1}}{\partial y}}(x,0)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7694ab4a0dabff5560b597e1170f9436f8804e)








