Instabilité de Kelvin-Helmholtz


L’instabilité de Kelvin-Helmholtz est un mouvement ondulatoire en dynamique des fluides qui se forme lorsque deux fluides thermiquement stables sont superposés et se déplacent à des vitesses différentes à leur surface de contact[1].
L'effet a été étudié au XIXe siècle par les physiciens Lord Kelvin et Hermann von Helmholtz qui ont montré que la différence de vitesse va engendrer un flot turbulent transversal à la frontière. La théorie peut être appliquée de la même façon à l'intérieur d'un fluide de densité uniforme mais ayant des couches se déplaçant à des vitesses différentes ou des fluides de densités différentes superposés.
Cette instabilité joue un rôle important dans de nombreuses situations géophysiques : dans la dynamique de l'atmosphère et des océans, dans le comportement des plasmas, etc. Les structures tourbillonnaires, onde ou lame de Kelvin-Helmholtz, résultant de l'instabilité contribuent de façon significative au transport de quantité de mouvement, de température et de polluants. La compréhension de la génération de ces instabilités permet de mieux les représenter dans les modèles dont la résolution n’est pas suffisante pour permettre de les résoudre explicitement.
Théorie[modifier | modifier le code]

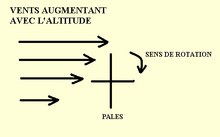
Pour de faibles vitesses de deux fluides glissant l'un par rapport à l'autre, l'interface, stabilisée par la gravité et la tension de surface, est horizontale. Pour une différence de vitesse critique à l'interface, on assiste à une déstabilisation et des ondes propagatives apparaissent et deviennent rapidement non-linéaires. L'instabilité est d'origine inertielle avec un seuil indépendant de la viscosité des fluides mais avec un taux de croissance et une vitesse des ondes affectés par la dissipation aux frontières. Pour une variation continue de densité et de vitesses, l'instabilité de Kelvin-Helmholtz est décrite par l'équation de Taylor-Goldstein et se développe à une certaine valeur du nombre de Richardson. Typiquement, l'écoulement devient instable pour un < 0,25 ce qui est assez commun dans les couches nuageuses.
L'écoulement du fluide est alors complètement décrit par son champ vectoriel de vitesse , son champ scalaire de pression la densité et la viscosité . Selon les équations de Navier-Stokes qui régissent le mouvement des fluides :
- La conservation de la masse se réduit à la non-divergence de la vitesse :
- La conservation de la quantité de mouvement devient :
À cause de la viscosité, la vitesse de déplacement à la frontière aura tendance à s'égaliser et donc on aura une gradation dans chacun des fluides de la vitesse entre celle originale dans le fluide et celle à la frontière (image du haut à droite). On introduit ainsi un cisaillement du déplacement et donc une rotation, un tourbillon, dans chacun des fluides près de la surface de contact. Les fluides doivent être stables thermiquement pour que la rotation se propage en aval de son point de création, autrement le cisaillement se propage sur une large couche dans la verticale et l'onde générée est très faible.
Observations[modifier | modifier le code]


Météorologie[modifier | modifier le code]
En météorologie, les variations de vitesses et de densité sont le plus souvent importantes à la frontière entre les nuages et l'air clair et c'est souvent là que l'on retrouve les ondes de Kelvin-Helmholtz. On peut retrouver les conditions nécessaires dans les flux en aval d'obstacles avec les vents forts au-dessus de ce dernier et presque nuls en dessous. Les ondes sont rendues visibles seulement s'il y a formation de nuages. Elles peuvent être dangereuses car elles sont le site de turbulence pour les avions.
Dans la nouvelle version de 2017 de l'Atlas international des nuages, l'Organisation météorologique mondiale donne le nom de Fluctus aux nuages formés par ce type d'ondes[2].
Océanographie[modifier | modifier le code]
En océanographie, on peut retrouver ces ondes dans la masse océanique lors de variation de densité dans la verticale, comme dans la thermocline, ou dans des variations horizontales, comme à la rencontre d'eau douce et d'eau salée à la sortie d'un fleuve. Les vagues peuvent être également associés en partie à cette instabilité.
Astronomie[modifier | modifier le code]
En astronomie, dans tout corps céleste ayant une atmosphère, étoile ou planète, on peut retrouver des conditions favorables à cette instabilité. Cette instabilité a également été observée à la surface d'un nuage interstellaire dans la nébuleuse d'Orion [3] et la couronne du Soleil [4].
Autre[modifier | modifier le code]
En physique nucléaire, elle peut être particulièrement importante dans l'étude de la fusion par confinement inertiel et de l'interface plasma-béryllium.
Notes et références[modifier | modifier le code]
- « Instabilité de Helmholtz, onde de Kelvin-Helmholtz et lames de Kelvin-Helmholtz », Glossaire météorologique, Eumetcal (consulté le )
- (en) « Manual on the Observation of Clouds and Other Meteors (WMO-No. 407) », International Cloud Atlas, Organisation météorologique mondiale, (consulté le ).
- (en) Olivier Berné, Núria Marcelino et José Cernicharo, « Waves on the surface of the Orion molecular cloud », Nature, vol. 466, , p. 947–949 (DOI 10.1038/nature09289, résumé)
- Karen C. Fox, « NASA's Solar Dynamics Observatory Catches "Surfer" Waves on the Sun », NASA-The Sun-Earth Connection: Heliophysics, NASA
Bibliographie[modifier | modifier le code]
- Kelvin, Lord (William Thomson), "Hydrokinetic solutions and observations," Philosophical Magazine, vol. 42, pages 362–377 (1871).
- Helmholtz, Hermann Ludwig Ferdinand von, "Über discontinuierliche Flüssigkeits-Bewegungen [On the discontinuous movements of fluids]," Monatsberichte der Königlichen Preussiche Akademie der Wissenschaften zu Berlin [Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin], vol. 23, pages 215 ff (1868).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Instabilité de Rayleigh-Taylor, une autre instabilité entre fluides
- Instabilité de Crow par une interaction entre deux tourbillons
- Circulation atmosphérique
Liens externes[modifier | modifier le code]
- Frédéric Lagoutière, « Instabilité de Kelvin-Helmholtz (animation) », sur Université Pierre-et-Marie-Curie







