Diffusion de la matière
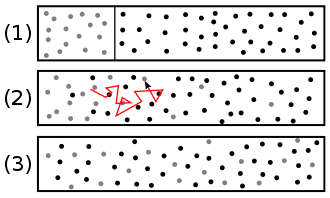
La diffusion de la matière, ou diffusion chimique, désigne la tendance naturelle d'un système à rendre uniforme le potentiel chimique de chacune des espèces chimiques qu'il comporte.
La diffusion chimique est un phénomène de transport irréversible qui tend à homogénéiser la composition du milieu. Dans le cas d'un mélange binaire et en l'absence des gradients de température et de pression, la diffusion se fait des régions de plus forte concentration vers les régions de concentration moindre[1]. Dans le cas le plus général la description précédente reste le plus souvent valable, mais l'on connaît des contre-exemples, où l'une des espèces migre d'une région de plus faible concentration vers une autre de concentration supérieure (uphill diffusion).
Historique[modifier | modifier le code]
D'un point de vue phénoménologique ce phénomène a d'abord été décrit par une loi énoncée par Adolf Fick[2] en 1855, par analogie avec l'équation de la chaleur introduite par Joseph Fourier[3] en 1822.
Cette relation entre le flux et gradient d'une quantité est très générale : conduction thermique, rayonnement dans un milieu opaque, perméation dans un milieu poreux, migration d'atomes sur une surface ou dans un cristal, etc. Elle résulte d'un changement d'échelle et de l'hypothèse d'une « petite perturbation » d'un état d'équilibre microscopique.
Cette loi, au départ empirique, a été justifiée et généralisée dans le cas d'un milieu multicomposant sous le nom d'équations de Stefan-Maxwell d'après les travaux de James Clerk Maxwell pour les gaz[4] en 1866 et Josef Stefan pour les liquides[5] en 1871. Cette généralisation montre l'effet des gradients de température ou de pression sur la diffusion[6]. Le cadre thermodynamique le plus général pour cette expression a été précisé par Lars Onsager[7].
Ce problème a reçu un nouvel éclairage avec la découverte de la loi de déplacement quadratique du mouvement brownien décrite par William Sutherland en 1904[8], Albert Einstein en 1905[9] et Marian Smoluchowski en 1906[10].
Cette loi est utilisée pour la diffusion dans les réseaux cristallins dont les mécanismes à l'échelle atomique ont été expliqués[11] par Yakov Frenkel[12] (1926), Carl Wagner et Walter Schottky[13] (1930).
Entre l'obtention des lois du mouvement brownien et leur application aux cristaux, une étape importante est obtenue par Sydney Chapman[14] (1916) et David Enskog[15] (1917) qui font le lien pour un gaz entre le niveau atomique et le niveau continu des équations de Navier-Stokes, permettant ainsi un calcul des coefficients de diffusion à partir des potentiels d'interaction moléculaires.
La seconde moitié du XXe siècle verra se développer les méthodes de changement d'échelle permettant d'écrire des lois macroscopiques à partir de la description du milieu à petite échelle. Ce sont des techniques permettant de justifier la loi de Darcy pour la perméation et de calculer la perméabilité (fluide). Elles sont de deux types :
- les méthodes de prise de moyenne volumique introduites par Stephen Whitaker[16] (1966) ;
- les méthodes d'homogénéisation mathématique introduites par Évariste Sanchez-Palencia[17] (1974) et développées par les mathématiciens français, en particulier Pierre-Louis Lions.
La dernière étape dans cette progression est le calcul direct du milieu (gaz ou solide) à l'échelle atomique par la dynamique moléculaire. Cette méthode constitue une expérience numérique. Elle est très lourde à effectuer et a attendu la venue des grands ordinateurs[18] (1953).
Vocabulaire et définitions[modifier | modifier le code]
- Le déplacement des atomes, ions ou molécules dans un milieu, que celui-ci soit solide (cristallin ou amorphe), liquide ou gazeux, est appelé de manière générale « migration ». Ceci est également valable pour le déplacement d'atomes sur une surface.
- L'advection désigne le déplacement d'ensemble des espèces dans un fluide. Elle est caractérisée par une vitesse qui est la vitesse barycentrique des espèces du milieu.
- La diffusion désigne le déplacement d'espèces venant se superposer à l'advection éventuelle. La vitesse de diffusion est l'écart entre la vitesse barycentrique de l'espèce considérée et la vitesse d'advection. Il en résulte que :
- la somme des flux massiques de diffusion est donc nulle par définition ;
- la somme des flux de diffusion molaires ne l'est pas ;
- le terme « interdiffusion » est un anglicisme qui, en français, contient une redondance interne.
- La perméation désigne le déplacement d'une espèce dans un milieu poreux. Il ne s'agit donc pas d'un phénomène de diffusion même si cette confusion est fréquente, y compris dans les textes techniques. On parle par exemple de diffusion gazeuse pour la séparation isotopique, alors qu'il s'agit d'un phénomène de perméation différentielle.
- le terme autodiffusion est une notion mathématique décrivant la diffusion d'une espèce dans elle-même, notion utile dans un milieu multiespèces. Ce terme désigne également la perméation d'une espèce dans un liquide ou un solide formé de la même espèce (voir figure).
- le terme « équation de diffusion » désigne une équation de conservation associée à des flux proportionnel aux gradients dans le milieu (concentration, température, pression : voir équations de Stefan-Maxwell).
Lois et coefficients de diffusion[modifier | modifier le code]
Les lois de diffusion telle que la loi de Fick expriment une relation linéaire entre le flux massique de matière (unité kg m−2 s−1) et le gradient de concentration où est une concentration massique (unité kg m−3) et une fraction massique :
Cette relation se transforme aisément pour exprimer le flux molaire dans un milieu incompressible :
où est la masse molaire et la concentration molaire (mol m−3).
Dans un milieu multiespèce, cette loi se généralise par les équations de Stefan-Maxwell.
(unité m2 s−1) est le coefficient de diffusion binaire de i dans j (ou de j dans i). Ce coefficient est caractéristique de la physique de l'interaction ij. Il est donc très différent suivant le type de phénomène étudié. Il est généralement de nature scalaire mais peut dans certains cas être un tenseur.
Milieux gazeux[modifier | modifier le code]
Le coefficient de diffusion binaire ne dépend que de l'interaction entre i et j (même si d'autres espèces sont présentes). La méthode de Chapman-Enskog permet de l'exprimer sous la forme suivante[6] :
avec
Nombre d'Avogadro, Constante de Boltzmann, Température, Masse molaire, Pression, Diamètre correspondant à la section efficace, Intégrale de collision réduite par sa valeur pour la collision de sphères dures et proche de 1.
L'intégrale de collision peut être calculée avec un potentiel intermoléculaire réaliste tel que le potentiel de Lennard-Jones.
Il existe des bases de données pour ces coefficients[6],[19]
Le coefficient de diffusion thermique est lié à la conductivité thermique et dépend, au contraire du coefficient de diffusion binaire, de toutes les espèces présentes. Il n'existe pas de forme explicite pour où est la fraction volumique et est la conductivité thermique[6]. On notera que ce coefficient s'exprime en kg m−1 s−1.
Milieux liquides[modifier | modifier le code]
La méthode la plus aboutie pour les liquides fait appel à la dynamique moléculaire, méthode numérique très lourde à mettre en œuvre. On se contente généralement de la loi de Stokes-Einstein, basée sur la loi de Stokes et celle du déplacement stochastique dans un mouvement brownien. Cette loi n'est en principe valide que lorsque la molécule i est notablement plus grosse que celles constituant le solvant j :
où est la viscosité dynamique. Le rayon de la sphère est choisi de telle façon que son volume soit égal au volume molaire :
Cette loi peut s'écarter de quelques dizaines de pour-cent de la mesure à cause de l'hypothèse sur la taille de la particule. Il existe des corrélations expérimentales utilisables pour toute espèce et corrigeant empiriquement l'expression de Stokes-Einstein[20].
Milieux poreux[modifier | modifier le code]
La perméation d'un gaz dans un milieu poreux peut s'effectuer sous divers régimes :
- si la dimension caractéristique de la porosité est grande devant le libre parcours moyen le phénomène est désigné classiquement par le terme perméation, décrite par la loi de Darcy qui est une loi de type diffusion obtenue par changement d'échelle, prise de moyenne volumique ou homogénéisation mathématique ;
- dans le cas contraire le milieu est décrit par l'équation de Darcy-Klinkenberg suivante, écrite pour une espèce seule (le cas général conduit à un système analogue aux équations de Stefan-Maxwell) :
avec
- la masse volumique du gaz,
- le coefficient de diffusion par gradient de concentration,
- le coefficient de diffusion par gradient thermique.
Au risque d'une certaine confusion, on parle de diffusion bien que cela ne soit pas rigoureusement le cas. En effet, que ce soit pour une ou plusieurs espèces comme dans le cas de la séparation isotopique, le flux total est non nul. Il s'agit donc en toute rigueur d'un phénomène de perméation. Les coefficients de diffusion dépendent des échanges d'énergie et de quantité de mouvement gaz-paroi au niveau microscopique[21].
Dans le cas d'un liquide la tension superficielle joue un rôle important pour les faibles dimensions de porosité, ce qui permet d'exclure ce phénomène de notre champ de discussion.
Solides[modifier | modifier le code]
Dans le cas des solides dont la porosité est trop faible pour que la perméation s'effectue par des mécanismes à l'échelle mésoscopique on parle de diffusion dans les solides[11]. Par rapport au cas précédent il n'existe pas de phase de vol libre pour la particule diffusante. Divers mécanismes peuvent intervenir :
- migration d'une lacune (atome manquant) ;
- migration d'un adatome (atome étranger ou atome du réseau cristallin en surnombre) dans un interstice ;
- expulsion (en anglais « kick-out ») d'un atome du réseau cristallin par la migration d'un adatome étranger : l'atome du réseau se retrouve en position intersticielle ;
- mécanisme de Franck-Turbull dans lequel l'adatome se retrouve piégé dans une lacune du réseau ;
- autodiffusion dans laquelle les atomes du réseau échangent leurs positions, ce mécanisme pouvant éventuellement intéresser plus de deux atomes ;
Enfin on mentionnera le cas où l'atome se lie chimiquement au réseau, l'exemple le plus courant étant l'oxydation des métaux.
Les mécanismes de diffusion (perméation) sont du type brownien. Ils sont donc décrits par une loi de Fick. Le saut d'un site du réseau cristallin à un autre se fait par franchissement d'une barrière de potentiel grâce à l'agitation thermique. Les coefficients de diffusion correspondants sont donc « activés », c'est-à-dire décrits par une loi d'Arrhenius :
où E est la barrière énergétique.
Surfaces[modifier | modifier le code]
Il existe une très forte analogie avec la diffusion (perméation) dans un cristal. Toutefois il peut y avoir de très fortes interactions entre les adatomes, lesquels peuvent couvrir entièrement la surface.
Notes et références[modifier | modifier le code]
- (en) Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch, Fundamentals of Analytical Chemistry, , 1072 p. (lire en ligne), p. 583.
- (de) A. Fick, « Über Diffusion », Annalen der Physik und Chemie, vol. 94, , p. 59–86 (lire en ligne).
- Joseph Fourier, Théorie analytique de la chaleur, [détail des éditions].
- (en) J. C. Maxwell, « On the dynamical theory of gases », The Scientific Papers of J. C. Maxwell, 1965, Volume 2, pp. 26–78 [1].
- (de) J. Stefan, « Über das Gleichgewicht und Bewegung, insbesondere die Diffusion von Gemischen », Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, 2te Abteilung a, 1871, 63, 63-124.
- (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, (ISBN 978-0-471-40065-3).
- (en) Lars Onsager, « Reciprocal Relations in Irreversible Processes. I », Physical Review, vol. 37, no 4, , p. 405–426.
- (en) William Sutherland, « A Dynamical Theory of Diffusion for Non-Electrolytes and Molecular Mass of Albumin », The Philosophical Magazine and Journal of Science, vol. 9, , p. 781-785 (lire en ligne).
- (de) Albert Einstein, « Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen », Annalen der Physik, vol. 17, no 8, , p. 549–560 (lire en ligne).
- (de) M. von Smoluchowski, « Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen », Annalen der Physik, vol. 21, , p. 756–780 (lire en ligne).
- (en) Helmut Mehrer, Diffusion in Solids, Springer-Verlag, (ISBN 978-3-540-71486-6).
- (de) Yakov Frenkel, « Über die Wärmebewegung in festen und flüssigen Körpern », Zeitschrift für Physik, vol. 35, , p. 652.
- (de) Carl Wagner et Walter Schottky, « Theorie der geordneten Mischphasen », Zeitschrift für Physik und Chemist B, vol. 11, , p. 163.
- (en) Sydney Chapman, « On the Law of Distribution of Molecular Velocities, and on the Theory of Viscosity and Thermal Conduction, in a Non-Uniform Simple Monatomic Gas », Philosophical Transactions of the Royal Society A, vol. 216, , p. 279-348.
- (de) David Enskog, « Kinetische Theorie der Vorgänge in maẞig verdünten Gasen », Thèse soutenue à l'université d'Uppsala, .
- Stephen Whitaker, « The equations of motion in porous media », Chemical Engineering Sciences, vol. 21, , p. 291-300.
- Enrique Sanchez-Palencia, « Comportement local et macroscopique d'un type de milieu physiques hétérogènes », International Journal of Engineering Sciences, vol. 12, no 1, , p. 331-351.
- Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller et Edward Teller, « Equation Of State Calculations by Fast Computing Machines », Journal of Chemical Physics, vol. 21, , p. 1087-1092 (lire en ligne).
- (en) T. R. Marrero et E. A. Mason, « Gaseous Diffusion Coefficients », Journal of Physical Chemistry Reference Data, vol. 1, no 1, (lire en ligne).
- (en) C. R. Wilke et Pin Chang, « Correlation of Diffusion Coefficients in Dilute Solutions », AIChE Jounal, (lire en ligne).
- (en) G. L. Vignoles, P. Charrier, Ch. Preux, B. Dubroca, Rarefied Pure Gas Transport in Non-isothermal Porous Media: Effective Transport Properties from Homogenization of the Kinetic Equation, Transport in Porous Media, Vol. 73, No. 2, June 2008, pp. 211-232 [2].
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) J. Crank, The mathematics of diffusion [« Mathématiques de la diffusion »], Oxford, Clarendon Press, , 2e éd., 414 p. (ISBN 0-19-853344-6).
Articles connexes[modifier | modifier le code]
- Diffusion ambipolaire
- Osmose
- Migration (matière)
- Conduction thermique
- Sorption
- Valeur de la Capacité Tampon Hydrique (VCTH ou MBV)
Liens externes[modifier | modifier le code]
- Diffusion mechanisms: atomic mechanisms [3]





























