Loi de Gumbel
En théorie des probabilités, la loi de Gumbel (ou distribution de Gumbel), du nom d'Émil Julius Gumbel, est une loi de probabilité continue. La loi de Gumbel est un cas particulier de la loi d'extremum généralisée au même titre que la loi de Weibull ou la loi de Fréchet. La loi de Gumbel est une approximation satisfaisante de la loi du maximum d'un échantillon de variables aléatoires indépendantes toutes de même loi, dès que cette loi appartient, précisément, au domaine d'attraction de la loi de Gumbel. Parmi les lois appartenant au domaine d'attraction de la loi de Gumbel, on compte la loi exponentielle[1].
La loi de Gumbel peut, par exemple, servir à prévoir le niveau des crues d'un fleuve, si on possède le relevé des débits sur dix ans. Elle peut aussi servir à prédire la probabilité d'un événement critique, comme un tremblement de terre.
Fonction de répartition[modifier | modifier le code]
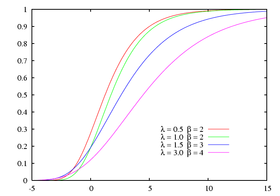
Etant donné deux paramètres et , la fonction de répartition de la loi de Gumbel est donné par :
Pour μ = 0 et β = 1, on obtient la loi standard de Gumbel.
Distributions associées[modifier | modifier le code]
- Si X suit une loi de Gumbel, alors la distribution conditionnelle de Y = -X dans le cas où Y est strictement positif, ou de façon équivalente, dans le cas où X est strictement négatif, suit une loi de Gompertz. La fonction de répartition G de Y est reliée à F la fonction de répartition de X, par la formule suivante : pour y > 0. Les densités sont donc reliées par : la densité de Gompertz (en) est proportionnelle à la densité de Gumbel réfléchie et restreinte aux valeurs strictement positives[2].
- Si X suit une exponentielle de moyenne égale à 1, alors –log(X) suit une distribution standard de Gumbel.
- Si alors .
La théorie associée aux lois log-gamma multivariées généralisées (en) fournit une version multivariée de la loi de Gumbel.
Voir aussi[modifier | modifier le code]
Notes[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gumbel distribution » (voir la liste des auteurs).
- Regular variation, Bingham, Goldie et Teugels.
- W.J. Willemse et R. Kaas, « Rational reconstruction of frailty-based mortality models by a generalisation of Gompertz' law of mortality », Insurance: Mathematics and Economics, vol. 40, no 3, , p. 468 (DOI 10.1016/j.insmatheco.2006.07.003)
Bibliographie[modifier | modifier le code]
- (en) N. H. Bingham, C. M. Goldie et J. L. Teugels, Regular Variation, Cambridge, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (no 27), , 1re éd., 516 p. (ISBN 978-0-521-37943-4, DOI 10.2277/0521379431, lire en ligne)






![{\displaystyle z=\exp \left[-{\frac {x-\mu }{\beta }}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fcc546b24629df176c493c4ca5f1819f5f7b634)
![{\displaystyle \exp(-\exp[-(x-\mu )/\beta ])\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95d027319f1ad9fe518dad014593a25a41431b93)
















