Loi de Yule-Simon

Loi de Yule–Simon
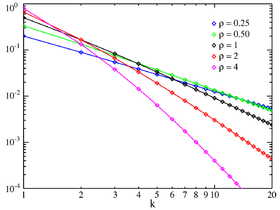Fonction de masse en échelle log-log (Les fonctions de masse ne sont définies que sur les entiers)
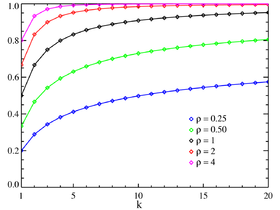Fonction de répartition (Les fonctions de répartition ne sont définies que sur les entiers)
Paramètres	$\rho >0$, paramètre de forme
Support	$k\in \{1,2,\dots \}\,$
Fonction de masse	$\rho \,\mathrm {B} (k,\rho +1)\,$
Fonction de répartition	$1-k\,\mathrm {B} (k,\rho +1)\,$
Espérance	${\frac {\rho }{\rho -1}}\,$ pour $\rho >1\,$
Mode	$1\,$
Variance	${\frac {\rho ^{2}}{(\rho -1)^{2}\;(\rho -2)}}\,$ pour $\rho >2\,$
Asymétrie	${\frac {(\rho +1)^{2}\;{\sqrt {\rho -2}}}{(\rho -3)\;\rho }}\,$ pour $\rho >3\,$
Kurtosis normalisé	$\rho +3+{\frac {11\rho ^{3}-49\rho -22}{(\rho -4)\;(\rho -3)\;\rho }}\,$ pour $\rho >4\,$
Fonction génératrice des moments	${\frac {\rho }{\rho +1}}\;{}_{2}F_{1}(1,1;\rho +2;e^{t})\,e^{t}\,$
Fonction caractéristique	${\frac {\rho }{\rho +1}}\;{}_{2}F_{1}(1,1;\rho +2;e^{i\,t})\,e^{i\,t}\,$

En théorie des probabilités et en statistique, la loi de Yule-Simon est une loi de probabilité discrète dont le nom est issu du statisticien George Udny Yule et de l'économiste et sociologue Herbert Simon. Simon la dénomma initialement loi de Yule. La loi dépend d'un paramètre de forme ρ, son support est infini.

Définition

La fonction de masse de la loi de Yule-Simon de paramètre ρ > 0 est :

$f(k;\rho )=\rho \,\mathrm {B} (k,\rho +1),\,$

pour tout entier k ≥ 1, où B est la fonction bêta. La fonction de masse peut également être écrite en utilisant le symbole de Pochhammer décroissant :

$f(k;\rho )={\frac {\rho \,\Gamma (\rho +1)}{(k+\rho )^{\underline {\rho +1}}}}$

où Γ est la fonction gamma. Ainsi, si ρ est entier,

$f(k;\rho )={\frac {\rho \,\rho !\,(k-1)!}{(k+\rho )!}}.$

La fonction de masse f possède la propriété suivante, pour k suffisamment grand :

$f(k;\rho )\approx {\frac {\rho \,\Gamma (\rho +1)}{k^{\rho +1}}}\propto {\frac {1}{k^{\rho +1}}}.$

Ceci signifie que la queue de la loi de Yule-Simon est une réalisation de la loi de Zipf : la fonction f peut être utilisée pour modéliser, par exemple, les fréquences relatives du k-ième mot le plus fréquent dans de grands textes qui, selon la loi de Zipf, est inversement proportionnel à la puissance typique de k.

Le paramètre ρ peut être estimé en utilisant un algorithme de point fixe.

Liens avec d'autres lois

La loi de Yule-Simon apparait initialement en tant que loi limite d'un cas particulier de processus stochastique étudié par Yule pour modéliser la répartition de taxons biologiques. Simon baptisa ce processus le processus de Yule, il est cependant plus connu aujourd'hui comme processus d'attachement préférentiel. Ce processus est problème d'urne dans lequel chaque boule est ajoutée à un nombre croissant d'urnes suivant une probabilité dépendant linéairement du nombre de boules déjà dans l'urne.

Cette loi apparait également comme mélange continu de lois géométriques. Plus spécifiquement, si W suit une loi exponentielle de paramètre ρ : $W\sim {\mathcal {E}}(\rho )$ avec densité $h(w;\rho )=\rho \,\exp(-\rho \,w)\,$, alors la variable aléatoire K de loi géométrique de paramètre e^-W suit la loi de Yule-Simon :

$K\sim {\mathcal {G}}(\exp(-W))\,$

La fonction de masse de la loi de Yule–Simon est alors le mélange exponentiel-géométrique suivant :

$f(k;\rho )=\int _{0}^{\infty }\,\,\,g(k;\exp(-w))\,h(w;\rho )\,dw$

où $g(k;p)=p\,(1-p)^{k-1}$ est la fonction de masse de la loi géométrique.

Généralisation

Une généralisation possible de la loi de Yule-Simon consiste à introduire un nouveau paramètre en remplaçant fonction bêta par la fonction bêta incomplète. La fonction de masse de la loi de Yule-Simon généralisée de paramètres ρ > 0 et 0 ≤ α < 1 est donnée par :

$f(k;\rho ,\alpha )={\frac {\rho }{1-\alpha ^{\rho }}}\mathrm {B} _{1-\alpha }(k,\rho +1).$

Pour α = 0 , on retrouve la loi de Yule-Simon standard.

Références

• (en) Colin Rose et Murray D. Smith, Mathematical Statistics with Mathematica : Mathematical Statistics with Mathematica, New York, Springer, 2002, 107 p. (ISBN 0-387-95234-9)