Un article de Wikipédia, l'encyclopédie libre.
loi d'Irwin-Hall
Densité de probabilité
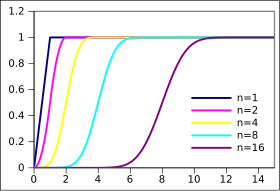
Fonction de répartition
Paramètres
n
∈
N
{\displaystyle n\in \mathbb {N} }
Support
x
∈
[
0
,
n
]
{\displaystyle x\in [0,n]}
Densité de probabilité
1
(
n
−
1
)
!
∑
k
=
0
⌊
x
⌋
(
−
1
)
k
(
n
k
)
(
x
−
k
)
n
−
1
{\displaystyle {\frac {1}{(n-1)!}}\sum _{k=0}^{\lfloor x\rfloor }(-1)^{k}{\binom {n}{k}}(x-k)^{n-1}}
Fonction de répartition
1
n
!
∑
k
=
0
⌊
x
⌋
(
−
1
)
k
(
n
k
)
(
x
−
k
)
n
{\displaystyle {\frac {1}{n!}}\sum _{k=0}^{\lfloor x\rfloor }(-1)^{k}{\binom {n}{k}}(x-k)^{n}}
Espérance
n
2
{\displaystyle {\frac {n}{2}}}
Médiane
n
2
{\displaystyle {\frac {n}{2}}}
Mode
{
toute valeur de
[
0
;
1
]
pour
n
=
1
n
2
sinon
{\displaystyle {\begin{cases}{\text{toute valeur de }}[0;1]&{\text{ pour }}n=1\\{\frac {n}{2}}&{\text{sinon}}\end{cases}}}
Variance
n
12
{\displaystyle {\frac {n}{12}}}
Asymétrie
0
Kurtosis normalisé
−
6
5
n
{\displaystyle -{\tfrac {6}{5n}}}
Fonction génératrice des moments
(
e
t
−
1
t
)
n
{\displaystyle {\left({\frac {\mathrm {e} ^{t}-1}{t}}\right)}^{n}}
Fonction caractéristique
(
e
i
t
−
1
i
t
)
n
{\displaystyle {\left({\frac {\mathrm {e} ^{\mathrm {i} t}-1}{\mathrm {i} t}}\right)}^{n}}
modifier
En théorie des probabilités et en statistique , la loi d'Irwin-Hall , dénommée d'après le statisticien Joseph Oscar Irwin et le mathématicien Philip Hall , est une loi de probabilité définie comme la somme de variables aléatoires indépendantes de loi uniforme continue [ 1] [0 ; 1] .
Pour générer des nombres pseudo-aléatoires ayant une loi approximativement normale , on peut générer, par simplicité, des sommes de nombres pseudo-aléatoires de loi uniforme continue .
Il ne faut pas confondre cette loi avec la loi de Bates qui est la moyenne de variables aléatoires uniformes sur [0 ; 1] .
La loi d'Irwin–Hall est la loi de probabilité continue pour la somme de n variables aléatoires iid de loi uniforme continue sur [0 ; 1] :
X
=
∑
k
=
1
n
U
k
.
{\displaystyle X=\sum _{k=1}^{n}U_{k}.}
Sa densité de probabilité est donnée par :
f
X
(
x
;
n
)
=
1
2
(
n
−
1
)
!
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
(
x
−
k
)
n
−
1
sgn
(
x
−
k
)
{\displaystyle f_{X}(x;n)={\frac {1}{2(n-1)!}}\sum _{k=0}^{n}\left(-1\right)^{k}{n \choose k}\left(x-k\right)^{n-1}\operatorname {sgn}(x-k)}
où sgn est la fonction signe :
sgn
(
x
−
k
)
=
{
−
1
x
<
k
0
x
=
k
1
x
>
k
.
{\displaystyle \operatorname {sgn} \left(x-k\right)={\begin{cases}-1&x<k\\0&x=k\\1&x>k.\end{cases}}}
ou encore par[ 2]
f
X
(
x
;
n
)
=
1
(
n
−
1
)
!
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
(
x
−
k
)
n
−
1
H
(
x
−
k
)
{\displaystyle f_{X}(x;n)={\frac {1}{(n-1)!}}\sum _{k=0}^{n}\left(-1\right)^{k}{n \choose k}\left(x-k\right)^{n-1}H(x-k)}
où H est la fonction de Heaviside :
H
(
x
−
k
)
=
{
0
x
<
k
1
x
>
k
.
{\displaystyle H\left(x-k\right)={\begin{cases}0&x<k\\1&x>k.\end{cases}}}
spline (fonction définie par morceaux par des polynômes) de degré n sur les nœuds 0, 1, ..., n . Plus précisément, pour x ∈ ]k , k +1[
f
X
(
x
;
n
)
=
1
(
n
−
1
)
!
∑
j
=
0
n
−
1
a
j
(
k
,
n
)
x
j
{\displaystyle f_{X}(x;n)={\frac {1}{(n-1)!}}\sum _{j=0}^{n-1}a_{j}(k,n)x^{j}}
où les coefficients aj (k ,n )k :
a
j
(
k
,
n
)
=
{
1
k
=
0
,
j
=
n
−
1
0
k
=
0
,
j
<
n
−
1
a
j
(
k
−
1
,
n
)
+
(
−
1
)
n
+
k
−
j
−
1
(
n
k
)
(
n
−
1
j
)
k
n
−
j
−
1
k
>
0
{\displaystyle a_{j}(k,n)={\begin{cases}1&k=0,j=n-1\\0&k=0,j<n-1\\a_{j}(k-1,n)+(-1)^{n+k-j-1}{n \choose k}{{n-1} \choose j}k^{n-j-1}&k>0\end{cases}}}
f
X
(
x
)
=
{
1
0
≤
x
≤
1
0
sinon
{\displaystyle f_{X}(x)={\begin{cases}1&0\leq x\leq 1\\0&{\text{sinon}}\end{cases}}}
f
X
(
x
)
=
{
x
0
≤
x
≤
1
2
−
x
1
≤
x
≤
2
{\displaystyle f_{X}(x)={\begin{cases}x&0\leq x\leq 1\\2-x&1\leq x\leq 2\end{cases}}}
f
X
(
x
)
=
{
1
2
x
2
0
≤
x
≤
1
1
2
(
−
2
x
2
+
6
x
−
3
)
1
≤
x
≤
2
1
2
(
x
2
−
6
x
+
9
)
2
≤
x
≤
3
{\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{2}}x^{2}&0\leq x\leq 1\\{\frac {1}{2}}\left(-2x^{2}+6x-3\right)&1\leq x\leq 2\\{\frac {1}{2}}\left(x^{2}-6x+9\right)&2\leq x\leq 3\end{cases}}}
f
X
(
x
)
=
{
1
6
x
3
0
≤
x
≤
1
1
6
(
−
3
x
3
+
12
x
2
−
12
x
+
4
)
1
≤
x
≤
2
1
6
(
3
x
3
−
24
x
2
+
60
x
−
44
)
2
≤
x
≤
3
1
6
(
−
x
3
+
12
x
2
−
48
x
+
64
)
3
≤
x
≤
4
{\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{6}}x^{3}&0\leq x\leq 1\\{\frac {1}{6}}\left(-3x^{3}+12x^{2}-12x+4\right)&1\leq x\leq 2\\{\frac {1}{6}}\left(3x^{3}-24x^{2}+60x-44\right)&2\leq x\leq 3\\{\frac {1}{6}}\left(-x^{3}+12x^{2}-48x+64\right)&3\leq x\leq 4\end{cases}}}
f
X
(
x
)
=
{
1
24
x
4
0
≤
x
≤
1
1
24
(
−
4
x
4
+
20
x
3
−
30
x
2
+
20
x
−
5
)
1
≤
x
≤
2
1
24
(
6
x
4
−
60
x
3
+
210
x
2
−
300
x
+
155
)
2
≤
x
≤
3
1
24
(
−
4
x
4
+
60
x
3
−
330
x
2
+
780
x
−
655
)
3
≤
x
≤
4
1
24
(
x
4
−
20
x
3
+
150
x
2
−
500
x
+
625
)
4
≤
x
≤
5
{\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{24}}x^{4}&0\leq x\leq 1\\{\frac {1}{24}}\left(-4x^{4}+20x^{3}-30x^{2}+20x-5\right)&1\leq x\leq 2\\{\frac {1}{24}}\left(6x^{4}-60x^{3}+210x^{2}-300x+155\right)&2\leq x\leq 3\\{\frac {1}{24}}\left(-4x^{4}+60x^{3}-330x^{2}+780x-655\right)&3\leq x\leq 4\\{\frac {1}{24}}\left(x^{4}-20x^{3}+150x^{2}-500x+625\right)&4\leq x\leq 5\end{cases}}}
La probabilité que X soit compris entre k et k +1 est égal à
1
n
!
⟨
n
k
⟩
{\displaystyle {\frac {1}{n!}}\left\langle {n \atop k}\right\rangle }
⟨
n
k
⟩
{\displaystyle \left\langle {n \atop k}\right\rangle }
nombre eulérien [ 2] La loi de la partie fractionnaire de X est une loi uniforme sur [0,1].
↑ (en) N. Balakrishnan , N.L. Jonhson et S. Kotz , Continuous Univariate Distributions , vol. 2, Wiley , 1995 , 2e éd. (ISBN 0-471-58494-0 , section 26.9↑ a et b (en) I. A. Salama et L. L. Kupper, « A Geometric Interpretation for the Eulerian Numbers », Amer. Math. Monthly vol. 93, no 1, janvier 1986 , p. 51-52 Irwin, J.O. (1927) "On the Frequency Distribution of the Means of Samples from a Population Having any Law of Frequency with Finite Moments, with Special Reference to Pearson's Type II". Biometrika , Vol. 19, No. 3/4., p. 225–239. DOI 10.1093/biomet/19.3-4.225 JSTOR :2331960 Hall, Philip . (1927) "The Distribution of Means for Samples of Size N Drawn from a Population in which the Variate Takes Values Between 0 and 1, All Such Values Being Equally Probable". Biometrika , Vol. 19, No. 3/4., p. 240–245. DOI 10.1093/biomet/19.3-4.240 JSTOR :2331961 


![{\displaystyle x\in [0,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a6353d734e3069864262a03b54fac28f8a64813)



![{\displaystyle {\begin{cases}{\text{toute valeur de }}[0;1]&{\text{ pour }}n=1\\{\frac {n}{2}}&{\text{sinon}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c98a2012f3932ecb343ca9d760a994b8b8836673)

















