Polygone
Un polygone[α], en géométrie euclidienne, est une figure géométrique plane formée d'une ligne brisée (appelée aussi ligne polygonale) fermée, c'est-à-dire d'une suite cyclique de segments consécutifs.
Les segments sont appelés bords ou côtés et les extrémités des côtés sont appelés sommets ou coins du polygone.
Un polygone est dit croisé si au moins deux côtés non consécutifs sont sécants, et simple si l'intersection de deux côtés est vide ou réduite à un sommet pour deux côtés consécutifs. La somme des angles d'un polygone simple (convexe ou non) ne dépend que de son nombre de sommets.
Dans le cas des polygones simples, on confond souvent le polygone et son intérieur en appelant polygone la surface délimitée par la ligne polygonale fermée[1].
La notion de polygone est généralisée :
- sur une surface, par des figures dont les côtés sont des segments d'orthodromie (ligne de plus court chemin), par exemple sur la sphère par les polygones sphériques (dont les côtés sont des arcs de grand cercle) ;
- en dimension 3 par les polyèdres et en dimension quelconque par les polytopes.

Vocabulaire de base
[modifier | modifier le code]Un polygone est constitué :
- d'une suite finie[β] de points du plan appelés sommets[γ] ;
- des segments reliant les couples de sommets consécutifs ainsi que d'un segment reliant le premier et le dernier point, tous ces segments étant appelés côtés.

Un polygone est en général désigné par la juxtaposition des lettres désignant les sommets, dans l'ordre de la suite.
La désignation d'un polygone en toute généralité s'écrit donc A1A2A3···An, constitué de n sommets et de n segments [A1, A2], [A2, A3], …, [An–1, An] et [An, A1].
Dans le cas d'un polygone simple, chaque sommet distinct de ses deux voisins est associé à un angle interne : c'est l'angle entre les deux côtés qui aboutissent au sommet.
Le périmètre d'un polygone est la somme des longueurs de ses côtés.
Ordre d'un polygone
[modifier | modifier le code]L'ordre d'un polygone est le nombre de ses côtés. C'est évidemment aussi le nombre de ses sommets ou celui de ses angles.
Éléments opposés
[modifier | modifier le code]- Si l'ordre d'un polygone est pair :
- les sommets séparés par côtés sont dits « opposés » entre eux ;
- même chose pour les angles correspondants ;
- les côtés séparés par sommets sont dits eux aussi « opposés » entre eux.
- Si l'ordre du polygone est impair, les côtés sont « opposés » aux sommets et aux angles (et vice-versa) ; plus précisément, chaque sommet (ou chaque angle) est « opposé » au côté situé sommets plus loin.
Côtés prolongés et diagonales
[modifier | modifier le code]Les droites qui portent les côtés d'un polygone sont appelées les côtés prolongés de ce polygone.
Une diagonale d'un polygone est un segment qui joint deux sommets non consécutifs, c'est-à-dire un segment qui joint deux sommets et qui n'est pas un côté du polygone.
Un polygone à n côtés possède ainsi diagonales.
Typologie des polygones
[modifier | modifier le code]Il existe de nombreuses manières de classer les polygones : en fonction de leur convexité, de leurs symétries, de leurs angles... Mais on les classe d'abord suivant leur nombre de côtés.
Classement suivant le nombre de côtés
[modifier | modifier le code]Les polygones peuvent être classés entre eux suivant leur ordre.
Les polygones d'ordre 1 et 2 sont dits dégénérés : ils correspondent respectivement à un point, et à un segment, et possèdent en particulier de ce fait une aire nulle.
Le polygone non dégénéré le plus élémentaire est le triangle.
Vient ensuite le quadrilatère, d'ordre 4.
À partir de l'ordre 5, chaque nom de polygone est formé d'une racine grecque correspondant à l'ordre du polygone suivie du suffixe -gone.
Pour s'y retrouver dans la dénomination des polygones, il faut retenir que -kai- signifie « et » en grec, et que -conta- signifie « dizaine ». Par exemple, le mot triacontakaiheptagone signifie trois (tria-) dizaines (-conta-) et (-kai-) sept (-hepta-) unités, et correspond donc à un polygone de trente-sept côtés, « et » étant interprété ici comme « plus »[2].
Au-delà de 12 côtés, la coutume est de parler de polygone à n côtés.
Il existe cependant plusieurs dénominations anciennes pour des nombres « ronds » comme pour un polygone à vingt côtés (icosa-), à cent côtés (hecto-), à mille côtés (chilio-) et à dix mille côtés (myrya-).
Les mêmes principes s'appliquent aux polyèdres, où il suffit de remplacer le suffixe -gone par le suffixe -èdre.
Classement par convexité
[modifier | modifier le code]Polygone croisé
[modifier | modifier le code]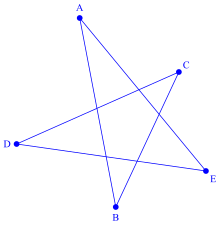
Un polygone est dit croisé si au moins deux de ses côtés sont sécants, c'est-à-dire si au moins deux de ses côtés non consécutifs se coupent[3]. C'est le cas du pentagone ABCDE ci-contre.
Polygone simple
[modifier | modifier le code]Un polygone est dit simple si deux côtés non consécutifs ne se rencontrent pas et deux côtés consécutifs n'ont en commun que l'un de leurs sommets[4]. Un polygone simple est toujours non croisé.
Il forme alors une courbe de Jordan, qui délimite une partie bornée du plan, appelée son intérieur. On appelle aire d'un polygone simple l'aire de son intérieur.
Polygone non convexe
[modifier | modifier le code]
Un polygone simple est dit non convexe si son intérieur n'est pas convexe, autrement dit si l'une de ses diagonales n'est pas entièrement dans son intérieur.
Par exemple, le pentagone simple ACDBE ci-contre est non convexe car les diagonales [B, C] et [C, E] ne sont pas dans l'intérieur du polygone. Le segment ouvert ]B, C[ est même complètement à l'extérieur. L'existence d'une telle « bouche » est une propriété générale des polygones simples non convexes[5].
Polygone convexe
[modifier | modifier le code]
Un polygone est dit convexe s'il est simple et si son intérieur est convexe. Ainsi, l'hexagone MNOPQR ci-contre est convexe.
Classement par symétrie
[modifier | modifier le code]Notion d'élément de symétrie
[modifier | modifier le code]

Les symétries d'un polygone d'ordre n sont les isométries du plan euclidien qui permutent à la fois ses n sommets et ses n côtés. Une telle application affine fixe nécessairement l'isobarycentre G des sommets donc ne peut être que de deux types :
- une symétrie axiale dont l'axe passe par G ;
- une rotation de centre G dont l'angle (en radians) est un multiple de 2π/n, ou encore : de la forme 2πp/q où p/q est une fraction irréductible et q est un diviseur de n (q est l'ordre de la rotation, qui indique combien de fois il faut appliquer la rotation pour revenir au point de départ : par exemple, la rotation d'ordre 2, c'est-à-dire d'angle π, est la symétrie de centre G).
L'ensemble des symétries de n'importe quelle figure plane est un sous-groupe du groupe des isométries du plan. En effet, lorsqu'on compose deux de ces symétries ou qu'on prend la bijection réciproque de l'une d'elles, le résultat est encore une symétrie de la figure.
Les symétries d'un polygone d'ordre n forment même un groupe fini, qui est égal, pour un certain diviseur d de n :
- ou bien au groupe cyclique Cd des d rotations d'angles multiples de 2π/d (si d = 1, c'est le groupe trivial, réduit à l'application identité : le polygone n'a aucun « élément de symétrie ») ;
- ou bien au groupe diédral Dd constitué de ces d rotations et de d symétries axiales (si d = 1, le seul « élément de symétrie » du polygone est alors un axe de symétrie).
Notion de polygone régulier
[modifier | modifier le code]
Un polygone d'ordre n est dit régulier s'il est équilatéral (côtés égaux) et équiangle (angles égaux), ou encore s'il est « le plus symétrique possible », c'est-à-dire si son groupe de symétrie est Dn. Il suffit pour cela que le polygone possède n axes de symétrie, ou encore : une rotation d'ordre n. Lorsqu'on dit « le polygone régulier d'ordre n », il s'agit de l'« unique » polygone convexe de cette famille (on calcule facilement son périmètre et son aire). Les autres sont dits étoilés[ζ].
- Quelques exemples et contre-exemples
- tout triangle équilatéral ou équiangle est régulier ;
- les quadrilatères à 4 sommets distincts :
- équiangles sont les rectangles ;
- équilatéraux sont les losanges ;
- réguliers sont donc les carrés.
Symétrie axiale
[modifier | modifier le code]
Le groupe de symétrie est diédral si et seulement si le polygone admet un axe de symétrie. Si le polygone n'est pas croisé, un tel axe passe nécessairement par un sommet ou le milieu d'un côté.[réf. nécessaire]
Plus précisément :
- dans un polygone non croisé d'ordre impair, tout axe de symétrie est bissectrice de l'angle interne en un sommet et médiatrice du côté opposé ;
- dans un polygone non croisé d'ordre pair, tout axe de symétrie est soit bissectrice de deux angles internes opposés, soit médiatrice de deux côtés opposés.
- Quelques exemples
- un triangle isocèle est symétrique par rapport à sa bissectrice principale ;
- les quadrilatères admettant un axe de symétrie sont les trapèzes isocèles, les cerfs-volants et les antiparallélogrammes ;
- les parallélogrammes admettant un axe de symétrie sont les losanges et les rectangles ;
- le rectangle, cas particulier de trapèze isocèle, possède deux axes de symétrie qui sont portés par ses médianes ;
- le losange, cas particulier de cerf-volant, possède deux axes de symétrie qui sont portés par ses diagonales ;
- le carré est un quadrilatère régulier donc il possède quatre axes de symétrie : ceux du losange et ceux du rectangle, dont il est un cas particulier.
- les parallélogrammes admettant un axe de symétrie sont les losanges et les rectangles ;
Symétrie centrale
[modifier | modifier le code]
Dans un polygone d'ordre n, pour que l'isobarycentre soit un centre de symétrie — c'est-à-dire pour que le groupe de symétrie Cd ou Dd contienne la rotation d'angle π — il faut et il suffit que d soit pair, donc il faut que n soit pair. Les côtés opposés sont alors parallèles et de même longueur.
Les quadrilatères non croisés possédant une symétrie centrale sont les parallélogrammes.
Classement par les angles
[modifier | modifier le code]Polygone équiangle
[modifier | modifier le code]Un polygone est dit équiangle quand tous ses angles internes sont égaux. Dans un polygone convexe équiangle à n côtés, chaque angle interne mesure (1 – 2/n)×180° (cf. § « Somme des angles » ci-dessous).
- Quelques exemples
- le seul triangle équiangle est le triangle équilatéral ;
- les quadrilatères équiangles sont les rectangles ;
- tous les polygones réguliers sont équiangles par définition.
Angles droits
[modifier | modifier le code]Un triangle rectangle comporte un angle droit et deux angles aigus.
Les quadrilatères convexes à au moins deux angles droits sont les trapèzes rectangles et les quadrilatères inscriptibles dont une diagonale est un diamètre (constitués de deux triangles rectangles accolés par leur hypoténuse), parmi lesquels on compte les cerfs-volants droits .
Les quadrilatères comportant au moins trois angles droits sont les rectangles.
Un polygone convexe ne peut présenter plus de quatre angles droits.
Autres classements
[modifier | modifier le code]Polygone inscriptible (dans un cercle)
[modifier | modifier le code]Un polygone est dit inscriptible quand tous ses sommets se trouvent sur un même cercle, dit cercle circonscrit au polygone. Ses côtés sont alors des cordes de ce cercle.
Parmi les quadrilatères inscriptibles, on trouve les trapèzes isocèles, les antiparallélogrammes et les cerfs-volants à deux angles droits.
Polygone circonscriptible (à un cercle)
[modifier | modifier le code]Un polygone est dit circonscriptible quand tous ses côtés sont tangents à un même cercle, dit cercle inscrit dans le polygone. Les anglophones et les germanophones ont baptisé « polygone tangent » ce type de polygone.
- Exemples de quadrilatères circonscriptibles
- Les parallélogrammes circonscriptibles sont les losanges.
- Les seuls quadrilatères circonscriptibles possédant deux côtés adjacents égaux sont les cerfs-volants.
- Le théorème de Pitot généralise ces deux énoncés.
Polygone bicentrique
[modifier | modifier le code]Un polygone à la fois inscriptible et circonscriptible est dit bicentrique. Les triangles et les polygones réguliers sont bicentriques.
Voir aussi : « Grand théorème de Poncelet » et « Quadrilatère bicentrique ».
Somme des angles
[modifier | modifier le code]


La somme des angles internes d'un polygone simple d'ordre n ne dépend pas de sa forme. Elle vaut (en radians et en degrés) :
En effet, cette formule, bien connue pour n = 3, se généralise en découpant le polygone en n – 2 triangles accolés deux à deux par un côté commun, qui est une diagonale de ce polygone (dans le cas particulier d'un polygone convexe, il suffit de considérer tous les segments joignant un certain sommet à tous les autres).
Une autre façon de démontrer cette formule[6] est de remarquer que (pour des angles orientés convenablement[7]) la somme des n angles externes est égale à 360° et les angles externe et interne associés à un même sommet ont pour somme 180°.
Polygones équivalents (combinatoire)
[modifier | modifier le code]
Deux polygones sont dits équivalents s'ils peuvent s'obtenir par rotation ou réflexion l'un de l'autre.
Ainsi pour il existe polygones non équivalents (suite A000940 de l'OEIS).
Parmi eux certains sont chiraux ( polygones chiraux pour côtés). Le nombre de polygones non équivalents par rotation seulement vaut donc (suite A000939 de l'OEIS).
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- du grec polus, nombreux, et gônia, angle
- Il s'agit plus exactement d'une suite cyclique, c'est-à-dire que le premier terme est le successeur du dernier et qu'un décalage des termes de la suite décrit le même polygone.
- Plusieurs sommets peuvent coïncider en un même point. Un sommet est donc plutôt un terme de la suite qu'une image dans le plan.
- Objet impossible en géométrie euclidienne mais en géométrie sphérique, on peut le représenter par un sommet placé sur un grand cercle.
- Dans la 6e de ses Méditations métaphysiques, Descartes se sert du chiliogone et du myriogone pour montrer la différence entre l'imagination et la conception pure.
- Notion qui, comme celles de polytope étoilé, de partie étoilée et de partie polygonale étoilée (en), formalise à sa façon l'intuition vague de « forme en étoile ».
Références
[modifier | modifier le code]- Voir, par exemple, l'article Polygone du dictionnaire Larousse.
- Samuel Verdan, « Systèmes numéraux en Grèce ancienne: description et mise en perspective historique », CultureMATH, (lire en ligne)
- Selon le glossaire Math en Jeans, il n'y a pas unanimité sur la notion, certains exigeant que la rencontre se fasse en un point différent d'un sommet et d'autres non.
- Glossaire de Math en Jeans.
- (en) Godfried Toussaint (en), « Anthropomorphic polygons », Amer. Math. Monthly, vol. 98, no 1, , p. 31-35 (DOI 10.2307/2324033, lire en ligne), « Theorem 2 (the One-Mouth theorem) ».
- Les deux méthodes sont données dans COJEREM, Des situations pour enseigner la géométrie : 1re/4e : notions pour l'élève, De Boeck, (ISBN 978-2-8041-2230-0, lire en ligne), p. 163-164 et Guide méthodologique (ISBN 978-2-8041-2231-7, lire en ligne), p. 134-153 pour le cas particulier d'un polygone convexe et dans (en) Martin Isaacs (en), Geometry for College Students, AMS, (lire en ligne), p. 13-14 pour le cas général.
- (en) William H. Press, Numerical Recipes, CUP, , 3e éd. (lire en ligne), p. 1123, Figure 21.4.4.









