Dodécagone
Un dodécagone est une figure de géométrie plane. C'est un polygone à douze sommets et côtés. Il possède 54 diagonales et la somme de ses angles est égale à 1800°[1].
Un dodécagone régulier est un dodécagone dont tous les côtés et tous les angles sont égaux. La forme régulière est construite au compas par la dissection de chaque côté d'un hexagone régulier. Le périmètre du dodécagone régulier donne une meilleure approximation de π que celle donnée par la mesure du périmètre de l'hexagone.
Sommaire |
Caractéristiques numériques du dodécagone régulier [modifier]
La relation entre le côté c du dodécagone et le rayon r de son cercle circonscrit est donnée par
L'apothème a (ou rayon du cercle inscrit) est donnée par
On en déduit un encadrement de π
L'aire 
du dodécagone régulier de côté c est donnée par :
Alternativement,
Construction du dodécagone régulier [modifier]
Un dodécagone régulier peut être construit à l'aide d'un compas et d'une règle. L'animation ci-dessous montre une manière en 23 étapes pour y parvenir. Le rayon du compas n'est pas modifié entre les étapes 8 à 11.
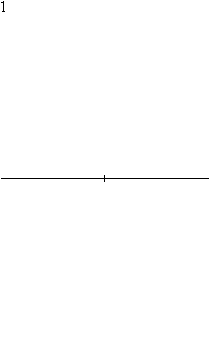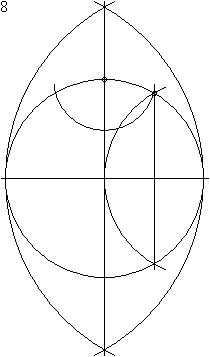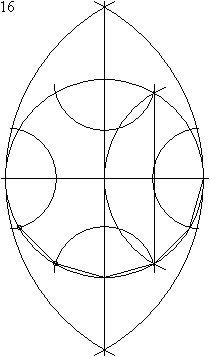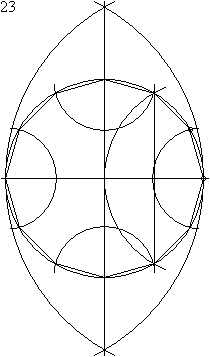
Pavage du plan à l'aide de dodécagone [modifier]
 pavage hexagonal tronqué |
 pavage grand rhombitrihexagonal |
 pavage semi-régulier : 3.3.4.12 & 3.3.3.3.3.3 |
Découpage [modifier]
Un découpage astucieux d'un dodécagone régulier en six figures géométriques (pentagones ou triangles) permet par réassemblage des pièces, de construire un carré.
D'autres découpages en huit, dix ou douze pièces permettent de reconstruire un triangle équilatéral, un pentagone, un décagone[2]. La possibilité de tels découpages est une conséquence du théorème de Wallace-Bolyai-Gerwien.
Notes [modifier]
- La somme des angles d'un polygone à n côtés est donnée par 180° × (n - 2)
- Dictionnaire de mathématiques récréatives
