Un article de Wikipédia, l'encyclopédie libre.
Un ennéadécagone ou ennéakaidécagone est un polygone à 19 sommets , donc 19 côtés et 152 diagonales .
La somme des angles internes d'un ennéadécagone non croisé vaut 3 060 degrés
Un ennéadécagone régulier comprend 19 côtés de même longueur et 19 angles internes de même mesure. Il y a neuf ennéadécagones réguliers : huit étoilés (les ennéadécagrammes notés {19/k } pour k de 2 à 9) et un convexe (noté {19}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'ennéadécagone régulier ».
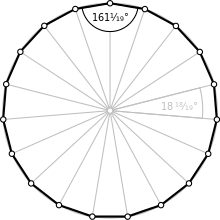
L'ennéadécagone régulier convexe {19} et ses angles remarquables .
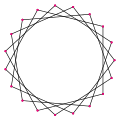
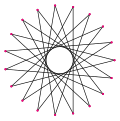
Les huit ennéadécagones réguliers étoilés
{19/2}
{19/3}
{19/4}
{19/5}
{19/6}
{19/7}
{19/8}
{19/9}
Caractéristiques de l'ennéadécagone régulier [ modifier | modifier le code ] Chacun des 19 angles au centre mesure
360
∘
19
≈
18,947
∘
{\displaystyle {\frac {360^{\circ }}{19}}\approx 18{,}947^{\circ }}
3
060
∘
19
≈
161,053
∘
{\displaystyle {\frac {3\,060^{\circ }}{19}}\approx 161{,}053^{\circ }}
Si a
le périmètre vaut
P
=
19
a
{\displaystyle P=19\,a}
l'aire vaut
A
=
19
4
a
2
cot
(
π
19
)
{\displaystyle A={\frac {19}{4}}\,a^{2}\cot \left({\frac {\pi }{19}}\right)}
l'apothème vaut
H
=
2
A
P
=
a
2
cot
(
π
19
)
{\displaystyle H={\frac {2\,A}{P}}={\frac {a}{2}}\cot \left({\frac {\pi }{19}}\right)}
le rayon vaut
R
=
H
cos
(
π
19
)
=
a
2
sin
(
π
19
)
{\displaystyle R={\frac {H}{\cos \left({\frac {\pi }{19}}\right)}}={\frac {a}{2\sin \left({\frac {\pi }{19}}\right)}}}
Sur les autres projets Wikimedia :
Triangles
Quadrilatères
Par nombre de côtés
1 à 10 côtés
11 à 20 côtés
30 côtés et plus
Autres classements que par le nombre des côtés
Classement par convexité
Classement par les angles et les côtés
Classement par rapport à un cercle
Polygones réguliers étoilés
Description
Droites et cercles remarquables
Relations entre polygones
Construction
Dissection