Triangle équilatéral
| Triangle équilatéral | |

| |
| Type | Polygone régulier |
|---|---|
| Arêtes | 3 |
| Sommets | 3 |
| Symbole de Schläfli | {3} |
| Diagramme de Coxeter-Dynkin | |
| Groupe de symétrie | Groupe diédral (D6) |
| Angle interne | 60° |
| Aire | √34a² |
| Périmètre | 3a |
| Propriétés | Constructible |
| modifier |
|
En géométrie euclidienne, un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Ses trois angles internes ont alors la même mesure de 60 degrés, et il constitue ainsi un polygone régulier à trois sommets.
Tous les triangles équilatéraux sont semblables. Chaque triangle équilatéral est invariant par trois symétries axiales et deux rotations[1] dont le centre est à la fois le centre de gravité, l'orthocentre et le centre des cercles inscrit et circonscrit au triangle.
La figure du triangle équilatéral apparait dans de nombreux contextes mathématiques et culturels.
Propriétés[modifier | modifier le code]
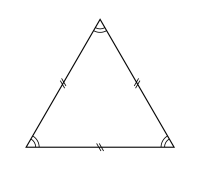
Angles[modifier | modifier le code]
À la différence des autres polygones, le triangle est une figure rigide, c'est-à-dire que la connaissance des longueurs des côtés détermine les mesures des angles internes, d'après le cas d'égalité des triangles issus des axiomes d'Euclide, ou sous une forme plus calculatoire avec le théorème d'Al Kashi. En particulier, dans le cas du triangle équilatéral, l'égalité des longueurs des côtés implique que les trois angles internes ont la même mesure. Or la somme des angles d'un triangle vaut 180°, donc chaque angle interne vaut un tiers de cette somme, donc 60°.
Éléments remarquables[modifier | modifier le code]

Comme un triangle équilatéral est isocèle en chacun de ses sommets, chaque médiane est aussi une hauteur, bissectrice, et portée par la médiatrice du côté opposé. Ce segment partage le triangle en deux triangles rectangles symétriques dont l'hypoténuse mesure le double d'un autre côté. En notant a la longueur commune aux trois côtés, le théorème de Pythagore permet de montrer que cette hauteur mesure , donc l'aire s'écrit . Le périmètre s'écrit simplement p = 3a.
La superposition des droites remarquables implique que le centre de gravité, situé aux deux tiers de la médiane en partant du sommet, est aussi le centre du cercle circonscrit qui passe par chacun des trois sommets. Le rayon de ce cercle vaut donc . Le cercle inscrit, de même centre, est tangent à chaque côté au bout d'un rayon qui lui est perpendiculaire, donc ce rayon est le dernier tiers de la médiane, et mesure .
Les trois cercles exinscrits ont pour rayon .
Le quotient de l'aire du disque inscrit dans un triangle équilatéral par l'aire du triangle est égal à π3√3 ≈ 0,604 599 (suite A073010 de l'OEIS).
Symétries[modifier | modifier le code]
Les médiatrices des côtés sont des axes de symétrie du triangle équilatéral, et les composées de ces symétries définissent deux rotations de 120° autour du centre du triangle. Avec l'identité, on obtient 6 transformations qui constituent le groupe de symétrie du triangle équilatéral, isomorphe au groupe diédral D6, d'ordre 6.
Parmi les triangles (non réduits à un point), seuls les triangles équilatéraux admettent autant de symétries.
Les sommets d'un triangle équilatéral peuvent être obtenus à partir de deux axes de symétrie formant un angle de 60° et d'un point appartenant à un seul des deux axes. La réflexion de ce point par rapport au deuxième axe forme un deuxième sommet, qui donne lieu ensuite au troisième sommet après réflexion par rapport au premier axe. Cette construction est illustrée par le diagramme de Coxeter-Dynkin constitué de deux points (représentant chacun un axe) reliés par une arête (signifiant l'angle de 60°) avec un anneau autour du premier point (représentant le sommet initial).
Le symbole de Schläfli {3} indique simplement le nombre de côtés pour un polygone régulier.
Caractérisation[modifier | modifier le code]
L'égalité des angles est caractéristique, c'est-à-dire que tout triangle équiangle (dont tous les angles internes ont la même mesure) est nécessairement équilatéral. D'autres caractérisations proviennent de problèmes d'optimisation pour lesquels le triangle équilatéral constitue la solution.
Le triangle équilatéral maximise l'aire intérieure du triangle pour un périmètre fixé. Il maximise aussi le rapport entre l'aire du cercle inscrit et l'aire du triangle, et le rapport entre l'aire du triangle et celle du cercle circonscrit, et par conséquent aussi le rapport entre le rayon du cercle inscrit et celui du cercle circonscrit.
Construction géométrique[modifier | modifier le code]

Pour construire un triangle équilatéral ayant pour côté un segment fixé à l'aide d'un compas, on peut :
- adapter l'ouverture du compas à la largeur du segment ;
- tracer deux arcs de cercle sécants en plaçant successivement la pointe du compas à chaque extrémité du segment
- relier à la règle un point d'intersection[2] des deux arcs aux deux extrémités du segment.
Pour construire un triangle équilatéral inscrit dans un cercle, on peut :
- adapter l'ouverture du compas au rayon du cercle ;
- placer la pointe du compas en un point du cercle ;
- tracer au compas deux arcs de cercle qui coupent le cercle initial en deux points distincts ;
- relier à la règle les deux points d'intersection ainsi formés et les relier au point où avait été placée la pointe du compas
Occurrences[modifier | modifier le code]

Les triangles équilatéraux peuvent être trouvés dans de nombreuses constructions géométriques (voir par exemple GeoGebra). Trois des cinq solides de Platon sont composés de triangles équilatéraux. En particulier, les quatre faces du tétraèdre régulier sont des triangles équilatéraux. Plus généralement, les 2-faces des simplexes réguliers en plus grande dimension comme le pentachore sont des triangles équilatéraux.
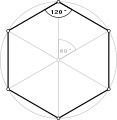
Le triangle équilatéral constitue une tuile du pavage triangulaire. En particulier, six triangles équilatéraux peuvent composer un hexagone régulier inscrit dans le cercle unité, ce qui permet de démontrer l'inégalité .
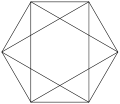
Deux triangles équilatéraux symétriques par rapport à leur centre commun forment un hexagramme.
-
Pavage triangulaire
-
Hexagone de périmètre 6 inscrit dans le cercle unité de longueur 2π
-
Hexagramme inscrit dans un hexagone
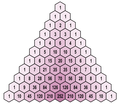
La forme du triangle équilatéral est utilisée pour figurer les nombres triangulaires et pour disposer les coefficients binomiaux du triangle de Pascal.
-
Premiers nombres triangulaires
-
Premières lignes du triangle de Pascal
-
Marquage de la parité des termes du triangle de Pascal, faisant apparaitre un triangle de Sierpiński
Le motif géométrique apparait aussi dans la construction du triangle de Sierpiński et du flocon de Koch.
-
Triangle initial
-
Première étape de construction du flocon de Koch
-
Deuxième étape
-
Troisième étape
-
Quatrième étape
Les racines troisièmes de l'unité 1, et forment un triangle équilatéral dans le plan complexe.
Le théorème de Morley est un résultat permettant de trouver un triangle équilatéral dans n'importe quel triangle.
Tout triangle « est » équilatéral, c'est-à-dire que tout triangle (non dégénéré) du plan affine est équilatéral pour un certain produit scalaire (unique à un multiple positif près)[3],[4].
Dans la culture[modifier | modifier le code]
- Plusieurs sites archéologiques ont des triangles équilatéraux dans leur construction, par exemple Lepenski Vir en Serbie.
- La figure apparaît également dans l'architecture moderne, comme dans le Jefferson National Expansion Memorial.
- Le triangle équilatéral a une signification mystique, étant une représentation de la trinité chrétienne dans The Two Babylons et faisant partie du Tetraktys, figure utilisée par les Pythagoriciens.
- Dans la signalisation routière, les panneaux d'avertissement de danger et ceux de cédez-le-passage ont une forme de triangle équilatéral, respectivement avec un sommet en haut et un sommet en bas.
Notes et références[modifier | modifier le code]
- En plus de la rotation triviale qu'est l'identité.
- Il peut y avoir deux points d'intersection pour les arcs de deux cercles distincts. Il suffit d'en choisir un des deux.
- Pierre Lecomte, Le mathématicien et ses esclaves, Éditions de l'université de Liège, (lire en ligne), p. 127.
- Cela revient à dire que les six transformations affines laissant invariant ce triangle sont des isométries pour une certaine distance euclidienne. Comparer avec « Espace euclidien, § Caractérisation par le groupe orthogonal ».
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Lien externe[modifier | modifier le code]
(en) Triangle équilatéral sur le site Math Open Reference, avec une animation interactive.