Polygone simple
En géométrie, un polygone est dit simple si deux côtés non consécutifs ne se rencontrent pas et deux côtés consécutifs n'ont en commun que l'un de leurs sommets[1], autrement dit, si ses segments forment une courbe de Jordan. Un polygone simple est topologiquement équivalent à un cercle.
Les polygones simples sont aussi appelés « polygones de Jordan[2] », en relation avec le théorème de Jordan qui établit que toute courbe fermée du plan qui « ne se recoupe pas » divise le plan en deux régions : l'intérieur et l'extérieur.
Polygone faiblement simple[modifier | modifier le code]
Si une ligne polygonale fermée du plan divise celui-ci en deux domaines tous les deux équivalents à un disque, alors la ligne polygonale est appelée un polygone faiblement simple. De manière moins formelle, un polygone faiblement simple peut avoir des côtés qui se touchent, mais qui ne se croisent pas. L'image ci-dessous montre un exemple d'un tel polygone (ici le polygone ABCDEFGHJKLM), avec la couleur bleue marquant l'intérieur.
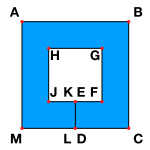
Les polygones faiblement simples (et non simples) sont utilisés en infographie, ainsi qu'en conception assistée par ordinateur, pour représenter des régions polygonales avec des trous : pour chaque trou dans la région, une "coupe" est créée, qui le relie à la frontière extérieure. Dans le dessin ci-dessus, ABCM est la frontière extérieure d'une région polygonale ayant un trou représenté par FGHJ. Le coupe ED connecte le trou avec l'extérieur, et est parcourue deux fois, ce qui résulte en une représentation par polygone faiblement simple.
Applications en géométrie algorithmique[modifier | modifier le code]
En géométrie algorithmique, certains problèmes calculatoires impliquent des entrées sous la forme de polygones simples. Dans chacun de ces problèmes, la distinction entre intérieur et extérieur est cruciale pour la définition du problème[3].
- Point dans un polygone (en) : test permettant de déterminer si un point P du plan se trouve à l'intérieur ou à l'extérieur du polygone.
- Des formules simples sont connues pour calculer l'aire d'un polygone, c'est-à-dire l'aire de l'intérieur du polygone.
- Triangulation d'un polygone : algorithme qui consiste à diviser un polygone simple en un nombre fini de triangles.
- L'enveloppe convexe d'un polygone simple peut être calculée plus facilement que celle d'un ensemble quelconque de points.
Notes et références[modifier | modifier le code]
- Glossaire de Math en Jeans.
- (en) Eric W. Weisstein, « Simple Polygon », sur MathWorld.
- (en) La FAQ comp.graphics.algorithms, qui référence des solutions à des problèmes impliquant des polygones 2D et 3D.
