Loi de Xenakis
| Loi de Xenakis | |
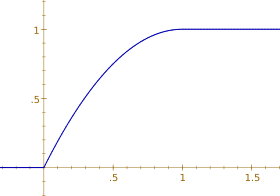 Fonction de répartition Fonction de répartition de la loi de Xenakis de paramètre 1; elle est proche de celle d'une loi exponentielle de paramètre e | |
| Paramètres | |
|---|---|
| Support | |
| Densité de probabilité | pour |
| Fonction de répartition | pour |
| Espérance | |
| Médiane | |
| Mode | 0 |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie | |
| Fonction génératrice des moments | |
| Fonction caractéristique | |
| modifier |
|
La loi de Xenakis est la loi d'une variable aléatoire positive, utilisée par Iannis Xenakis en musique stochastique, par exemple pour les durées des notes et leur variation de hauteur[1].
Définition
[modifier | modifier le code]La loi de Xenakis est la loi de la longueur d'un segment inclus dans un segment de longueur a[2]. C'est donc une loi triangulaire de paramètres 0, a et 0.
Propriétés
[modifier | modifier le code]Densité
[modifier | modifier le code]La densité de la loi de Xenakis est, dans sa forme standard, une fonction affine sur [0 , a] s'annulant en a.
Le paramètre a est donc un paramètre d'échelle ; la forme standard de la loi de Xenakis ne présente pas de paramètre de position.
Fonction de répartition
[modifier | modifier le code]La fonction de répartition de la loi de Xenakis est du second degré. Par conséquent, on peut simuler celle-ci à l'aide d'une loi uniforme continue. En effet, si X est une variable aléatoire uniforme sur [0 ; 1], est une variable aléatoire de Xenakis de paramètre a.
Loi de Xenakis de paramètres affines fixés
[modifier | modifier le code]Loi de Xenakis de paramètre 1
[modifier | modifier le code]La loi de Xenakis sur [0 ; 1] est une loi bêta de paramètres 1 et 2. On peut donc définir la loi de Xenakis de paramètre 1 comme la loi du minimum de deux variables aléatoires uniformes sur [0 ; 1].
Loi de Xenakis centrée réduite
[modifier | modifier le code]La loi de Xenakis centrée réduite, donc d’espérance 0 et d’écart type 1, est définie sur par :
- .
Distributions associées
[modifier | modifier le code]- Le minimum de deux variables aléatoires de Xenakis de paramètre 1 suit une loi bêta de paramètres 1 et 4.
Simulation
[modifier | modifier le code]Pour simuler une variable de Xenakis de paramètre 1 à partir de variables uniformes sur [0 ; 1], on a le choix entre trois méthodes :
- la définition, en rappelant que la distance entre deux nombres est la valeur absolue de leur différence ;
- Le fait qu'une variable de Xenakis est une variable de loi bêta, le minimum de deux nombres étant assez rapide à calculer (cette façon de faire n'était apparemment pas connue de Xenakis) ;
- l'utilisation de l'inverse de la fonction de répartition, qui est d'ailleurs celle utilisée par Xenakis[3].
Notes et références
[modifier | modifier le code]- Iannis Xenakis, Musiques formelles : nouveaux principes formels de composition musicale, Paris, Stock/Musique, , 260 p. (ISBN 2-234-01510-3, BNF 36143274), Annexe
- Musiques formelles, chapitre 1
- Musiques formelles, appendice
- « Musiques formelles »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), sur iannis-xenakis.org (consulté le )


![{\displaystyle x\in [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90edb65c670b1eff2a7bc52d4b09de483d029f7f)

![{\textstyle x\in [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3ae322ac31a2cf83c5341f6c3d43541c6cf8099)









![{\displaystyle p(x)={\begin{cases}{\frac {2}{a}}\left(1-{\frac {x}{a}}\right)&{\text{ si }}x\in [0,a]\\0&{\text{ sinon.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/249df692bc93b36f702eaea0f36e8664c039171d)

![{\displaystyle F(x)={\begin{cases}0&{\text{ si }}x<0\\1-{\frac {(x-a)^{2}}{a^{2}}}&{\text{ si }}x\in [0,a]\\1&{\text{ si }}x\geqslant a.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78520e36d527fc72bb6430b3b7e8fa32521ca7d8)
![{\displaystyle [-{\sqrt {2}};2{\sqrt {2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/802a16640968a47a6b571d6e49caa30480879a11)
