Matrice de rotation

En mathématiques, et plus précisément en algèbre linéaire, une matrice de rotation Q est une matrice orthogonale de déterminant 1, ce qui peut s'exprimer par les équations suivantes : Q^tQ = I = QQ^t et det Q = 1, où Q^t est la matrice transposée de Q, et I est la matrice identité.

${\begin{pmatrix}\cos \theta &-\sin \theta \\[3pt]\sin \theta &\cos \theta \\\end{pmatrix}}$

Expression de la matrice de rotation du vecteur OM, d'angle θ
dans le plan muni d'un repère orthonormé direct.

Ces matrices sont exactement celles qui, dans un espace euclidien, représentent les isométries (vectorielles) directes. Ces dernières sont aussi appelées rotations vectorielles (d'où le nom de « matrice de rotation »), parce qu'en dimension 2 et 3, elles correspondent respectivement aux rotations affines planes autour de l'origine et aux rotations affines dans l'espace autour d'un axe passant par l'origine.

En dimension 3, ces matrices sont utilisées intensivement pour les calculs de géométrie, de physique et en infographie.

L'ensemble de toutes les matrices de rotation de taille fixée forme un groupe appelé groupe des rotations ou groupe spécial orthogonal. C'est un sous-groupe du groupe orthogonal.

Définition et propriétés générales

Une propriété caractéristique des rotations du plan ou de l'espace est de conserver le caractère orthonormé direct des repères. Traduisant cela dans le langage des matrices, on démontre que la matrice $Q$ d'une application linéaire qui conserve les angles et les distances (une isométrie vectorielle) doit être orthogonale, c'est-à-dire que son inverse est égale à sa transposée : $Q^{t}=Q^{-1}\iff QQ^{t}=I$. De plus, la conservation de l'orientation se traduit par la formule $\det Q=+1$. Les matrices vérifiant ces propriétés sont appelées matrices de rotation.

Le produit de deux matrices de rotation est une matrice de rotation :

${\begin{aligned}(Q_{1}Q_{2})^{t}(Q_{1}Q_{2})&{}=Q_{2}^{t}(Q_{1}^{t}Q_{1})Q_{2}=I\\\det(Q_{1}Q_{2})&{}=(\det Q_{1})(\det Q_{2})=+1\end{aligned}}$

Pour n plus grand que 2, la multiplication de matrices de rotation n×n n'est pas commutative.

${\begin{aligned}Q_{1}&{}={\begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}}&Q_{2}&{}={\begin{pmatrix}0&0&1\\0&1&0\\-1&0&0\end{pmatrix}}\\Q_{1}Q_{2}&{}={\begin{pmatrix}0&-1&0\\0&0&1\\-1&0&0\end{pmatrix}}&Q_{2}Q_{1}&{}={\begin{pmatrix}0&0&1\\1&0&0\\0&1&0\end{pmatrix}}\end{aligned}}$

Remarquant que toute matrice identité est une matrice de rotation, et que la multiplication des matrices est associative, on peut résumer ces propriétés en disant que les matrices de rotation n×n forment un groupe, qui pour n > 2 est non abélien. Appelé le groupe spécial orthogonal, et noté SO(n), SO(n, R), SO_n, ou SO_n(R), ce groupe est isomorphe au groupe des rotations d'un espace à n dimensions, ce qui veut dire que la multiplication des matrices de rotation correspond à la composition des rotations, appliquée dans le même ordre (de la gauche vers la droite) que celui des matrices correspondantes.

Rotations en deux et trois dimensions

Dans toute cette section, on considère que les matrices agissent sur des vecteurs colonne.

Un point A du plan est de coordonnées (x , y) dans le repère orthonormé (O, x , y) de sens direct.

En dimension deux

Calcul de la rotation d'angle $\theta$ du vecteur ${\overrightarrow {OA}}$ à l'aide de la matrice de rotation :
${\begin{pmatrix}A'_{x}\\A'_{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{pmatrix}}{\begin{pmatrix}A_{x}\\A_{y}\end{pmatrix}}$

En deux dimensions, les matrices de rotation ont la forme suivante :

$R(\theta )={\begin{pmatrix}\cos \theta &-\sin \theta \\[3pt]\sin \theta &\cos \theta \\\end{pmatrix}}$ rotation d'angle θ du vecteur OA

Cette matrice permet de calculer les coordonnées du point A' dans le repère (O, x , y) inchangé, après que le vecteur OA a tourné d'un angle θ dans le sens trigonométrique.

$R'(\theta )={\begin{pmatrix}\cos \theta &\sin \theta \\[3pt]-\sin \theta &\cos \theta \\\end{pmatrix}}$ rotation d'angle θ du repère (O, x , y)

Cette matrice permet de calculer les coordonnées du point A dans le nouveau repère (O, x' , y'), après rotation du repère initial d'un angle θ dans le sens trigonométrique. On remarquera que cette matrice est la matrice transposée de la matrice précédente, en effet si l'on fait tourner d'un même angle d'une part le vecteur et d'autre part le repère, c'est-à-dire que rien n'a changé, est traduit par le fait que le produit des deux matrices est la matrice unité.

En dimension trois

Les matrices de base

Dans un espace euclidien à 3 dimensions, les matrices de rotations suivantes correspondent à des rotations du vecteur OA, d'un angle θ, autour des axes x, y et z (respectivement) :

$R_{\mathbf {x} }(\theta )={\begin{pmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\0&\sin \theta &\cos \theta \end{pmatrix}},\qquad R_{\mathbf {y} }(\theta )={\begin{pmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0&\cos \theta \end{pmatrix}},\qquad R_{\mathbf {z} }(\theta )={\begin{pmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}.$

Cette écriture fait immédiatement apparaitre que lors d'une rotation d'axe $X,x_{A}$ reste inchangé, que lors d'une rotation d'axe $Y,y_{A}$ reste inchangé et que lors d'une rotation d'axe $Z,Z_{A}$ reste inchangé.

Les matrices transposées de ces matrices permettent d'établir les coordonnées du point A après rotation du repère (O, x , y, z) d'un angle θ, soit :

$R_{\mathbf {x} }(\theta )={\begin{pmatrix}1&0&0\\0&\cos \theta &\sin \theta \\0&-\sin \theta &\cos \theta \end{pmatrix}},\qquad R_{\mathbf {y} }(\theta )={\begin{pmatrix}\cos \theta &0&-\sin \theta \\0&1&0\\\sin \theta &0&\cos \theta \end{pmatrix}},\qquad R_{\mathbf {z} }(\theta )={\begin{pmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}.$

Les rotations du repère opèrent ainsi : R_x tourne l'axe y vers l'axe z, R_y tourne l'axe z vers l'axe x et R_z tourne l'axe x vers l'axe y. Voir aussi la section #Dimensions emboîtées.

Dans un espace orienté

Si l'on oriente l'espace en trois dimensions avec les conventions habituelles (x vers l'observateur, y vers la droite et z vers le haut), ces rotations se font dans le sens contraire aux aiguilles d'une montre lorsque le troisième axe (celui qui ne subit pas la rotation) est dirigé vers l'observateur. En pratique, pour déterminer le sens de rotation, on peut utiliser la règle de la main droite.

Composition de rotations élémentaires

Toute rotation peut être décomposée en rotations élémentaires autour de chacun des axes d'un repère orthonormé arbitrairement défini. La matrice de rotation d'une rotation composée s'obtient par la multiplication des matrices de rotation élémentaires qui composent la rotation composée. Il est important de noter que ces multiplications ne sont pas commutatives, c'est-à-dire que, dans le cas général,

$R_{u}(\alpha ).R_{v}(\beta )\neq R_{v}(\beta ).R_{u}(\alpha )$

En dynamique du véhicule par exemple, le produit

$R_{z}(\alpha )\,R_{y}(\beta )\,R_{x}(\gamma )\,\!$

représente une rotation dont le lacet, le tangage et le roulis (également appelé angles de Cardan) sont respectivement α, β et γ, dans l'ordre suivant et selon les axes suivants :

• Rotation d'angle α autour de l'axe Z₀,
• Rotation d'angle β autour de l'axe Y₁ (Y après la rotation d'angle α),
• Rotation d'angle γ autour de l'axe X₂, (X après rotations d'angle α et β)

De la même façon, le produit

$R_{z}(\gamma )\,R_{x}(\beta )\,R_{z}(\alpha )\,\!$

représente une rotation dont les angles d'Euler sont α, β et γ (en utilisant la convention z-x-z pour les angles d'Euler).

Axe de rotation

Les matrices de rotations en trois dimensions ont un axe, c'est-à-dire une coordonnée (direction) laissée inchangée par la rotation.

Une rotation R autour d'un axe dirigé par ${\overrightarrow {u}}$ peut être décomposée à l'aide de 3 endomorphismes P, (I – P) et Q (cliquer sur l'image pour l'agrandir).

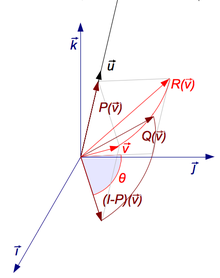
Axe à partir d'une matrice de rotation

Étant donné une matrice de rotation R, on peut trouver une matrice colonne u représentant le vecteur dirigeant l'axe en résolvant l'équation :

$R{\textbf {u}}={\textbf {u}}$ (correspondant à la recherche d’un vecteur propre de la matrice)

Matrice de rotation à partir d'un axe et d'un angle

On peut calculer la matrice R de rotation autour d'un axe dirigé par un vecteur unitaire ${\overrightarrow {u}}{\begin{pmatrix}{u_{x}}\\u_{y}\\u_{z}\end{pmatrix}}$ (donc avec u_x² + u_y² + u_z² = 1) et d'un angle θ. La formule est :

$R={\begin{pmatrix}u_{x}^{2}(1-c)+c&u_{x}u_{y}(1-c)-u_{z}s&u_{x}u_{z}(1-c)+u_{y}s\\[3pt]u_{x}u_{y}(1-c)+u_{z}s&u_{y}^{2}(1-c)+c&u_{y}u_{z}(1-c)-u_{x}s\\[3pt]u_{x}u_{z}(1-c)-u_{y}s&u_{y}u_{z}(1-c)+u_{x}s&u_{z}^{2}(1-c)+c\end{pmatrix}}$

où

$c=\cos \theta ,\qquad s=\sin \theta$

Si l'espace en 3 dimensions est orienté de façon conventionnelle, cette rotation se fera dans le sens inverse aux aiguilles d'une montre pour un observateur placé de telle sorte que le vecteur directeur ${\overrightarrow {u}}$ pointe dans sa direction (règle de la main droite).

Forme simplifiée de la formule axe-angle

Cette formule peut être simplifiée en

$R=P+\cos(\theta )(I-P)+\sin(\theta )Q=I+\sin(\theta )Q+(1-\cos(\theta ))Q^{2}$

où

$P={\begin{pmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\\u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\\u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}\end{pmatrix}}={\textbf {u}}\,{\textbf {u}}^{t},\qquad I={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}},\qquad Q={\begin{pmatrix}0&-u_{z}&u_{y}\\u_{z}&0&-u_{x}\\-u_{y}&u_{x}&0\end{pmatrix}}$

I est la matrice identité 3 × 3. La matrice Q est la représentation antisymétrique de ${\overrightarrow {u}}$, correspondant à l'application linéaire ${\overrightarrow {v}}\mapsto {\overrightarrow {u}}\wedge {\overrightarrow {v}}$ (où $\wedge$ est le produit vectoriel). La matrice $P=I+Q^{2}$ est la projection sur l'axe de rotation et $I-P=-Q^{2}$ est la projection sur le plan orthogonal à l'axe dirigé par ${\overrightarrow {u}}$.

En dimension supérieure

Ce qui précède peut être généralisé à une dimension n quelconque. L' « axe » de la rotation sera un sous-espace vectoriel de dimension n–2 dont tous les vecteurs sont fixes par la rotation, et pour un tel sous-espace A, les rotations d' « axe » commun A correspondent aux rotations du plan orthogonal à cet axe (et se composent de la même manière).

Mais en dimension supérieure à 3, le fait nouveau est qu'une rotation n'est pas nécessairement de cette forme (i.e. le sous-espace de ses vecteurs fixes peut très bien être de dimension strictement inférieure à n–2) : c'est seulement un produit de rotations de cette forme (cf exemples ci-dessous).

Exemples

• La matrice de rotation 2×2

$Q={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$

correspond à une rotation de 90° dans le plan.

• La matrice symétrique 2×2

$M={\begin{pmatrix}0,936&0,352\\0,352&-0,936\end{pmatrix}}$

est sa propre inverse mais comme son déterminant vaut −1, ce n'est pas une matrice de rotation ; il s'agit de la symétrie orthogonale par rapport à la droite d'équation 11y = 2x.

• La matrice de rotation 3×3

$Q={\begin{pmatrix}1&0&0\\0&{\frac {\sqrt {3}}{2}}&{\frac {1}{2}}\\0&-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}\end{pmatrix}}$

correspond à une rotation dans l'espace à 3 dimensions de −30° autour de l'axe des x.

• La matrice de rotation 3×3

$Q={\begin{pmatrix}0,36&0,48&-0,8\\-0,8&0,6&0\\0,48&0,64&0,60\end{pmatrix}}$

correspond à une rotation dans l'espace à 3 dimensions d'environ −74° autour de l'axe dirigé par ${\overrightarrow {u}}{\begin{pmatrix}-{\frac {1}{3}}\\{\frac {2}{3}}\\{\frac {2}{3}}\end{pmatrix}}$.

• La matrice de permutation 3×3

$P={\begin{pmatrix}0&0&1\\1&0&0\\0&1&0\end{pmatrix}}$

est également une matrice de rotation, comme toute matrice de permutation paire (mais jamais d'une permutation impaire).

• La matrice 3×3

$M={\begin{pmatrix}3&-4&1\\5&3&-7\\-9&2&6\end{pmatrix}}$

a un déterminant égal à +1, mais sa transposée n'est pas son inverse, donc ce n'est pas une matrice de rotation.

• La matrice 4×3

$M={\begin{pmatrix}0,5&-0,1&0,7\\0,1&0,5&-0,5\\-0,7&0,5&0,5\\-0,5&-0,7&-0,1\end{pmatrix}}$

n'est pas carrée et ne peut donc pas être une matrice de rotation, bien que $M^{t}\cdot M$ soit la matrice identité 3×3 (les colonnes sont orthonormales).

• La matrice de rotation 4×4

$Q={\begin{pmatrix}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}$

n'a pas d'axe de rotation : elle transforme tout vecteur en son opposé.

• La matrice de rotation 5×5

$Q={\begin{pmatrix}0&-1&0&0&0\\1&0&0&0&0\\0&0&-1&0&0\\0&0&0&-1&0\\0&0&0&0&1\end{pmatrix}}$

fait tourner les vecteurs du plan des deux premières coordonnées de 90°, fait tourner les vecteurs du plan des deux coordonnées suivantes de 180°, et laisse l'axe de la dernière coordonnée inchangé.

Ambiguïtés de la représentation matricielle

Alias et alibi pour les rotations

L'interprétation d'une matrice de rotation peut donner naissance à plusieurs ambiguïtés :

Changement de repère ou déplacement

La modification des coordonnées d'un vecteur peut correspondre à une rotation de ce vecteur (alibi), ou à une rotation du repère (alias).

Repère direct ou inverse

La matrice peut représenter la rotation dans un repère orienté positivement ou négativement.

Référentiel fixe ou mobile

Les axes de coordonnées peuvent être fixés ou tourner avec un solide.

Vecteurs ou formes linéaires

L'espace vectoriel admet un espace dual constitué des formes linéaires sur cet espace, et la matrice peut agir sur les vecteurs ou sur les formes.

Dans la plupart des cas, l'autre interprétation correspondrait à la matrice transposée (donc inverse).

Décompositions

Plans indépendants

On considère la matrice de rotation 3×3

$Q={\begin{pmatrix}0,36&0,48&-0,8\\-0,8&0,60&0\\0,48&0,64&0,60\end{pmatrix}}.$

Si, dans une certaine direction v, Q agit comme une multiplication par un facteur λ (autrement dit si v est un vecteur propre, de valeur propre associée λ), nous aurons

$Q\mathbf {v} =\lambda \mathbf {v} ,\,\!$

donc

$\mathbf {0} =(\lambda I-Q)\mathbf {v} .\,\!$

Ainsi λ est une racine du polynôme caractéristique de Q,

${\begin{aligned}0&{}=\det(\lambda I-Q)\\&{}=\lambda ^{3}-{\tfrac {39}{25}}\lambda ^{2}+{\tfrac {39}{25}}\lambda -1\\&{}=(\lambda -1)(\lambda ^{2}-{\tfrac {14}{25}}\lambda +1)\end{aligned}}$

On remarquera deux propriétés importantes. D'une part, l'une des racines est 1, ce qui nous dit qu'une certaine direction est laissée fixe par la matrice. Pour les rotations en trois dimensions, c'est l'axe de la rotation (un concept qui se généralise uniquement aux dimensions impaires). D'autre part, les deux autres racines sont complexes conjuguées, de produit 1 (le terme constant du polynôme du second degré), et dont la somme est 2 cos θ (l'opposé du terme de degré 1). Le même phénomène se produit pour toutes les matrices de rotation 3×3 (avec deux cas particuliers : pour une rotation nulle les "valeurs complexes conjuguées " valent en fait toutes deux 1, et pour une rotation de 180°, toutes deux valent −1). En fait, une factorisation analogue existe pour n'importe quelle matrice de rotation n×n. Si la dimension, n, est impaire, il y aura une valeur propre supplémentaire valant 1, et en toute dimension le reste du polynôme se factorisera en termes du second degré comme celui que nous avons vu (avec les deux cas particuliers déjà mentionnés). Le polynôme caractéristique sera toujours de degré n ; il y aura donc n valeurs propres ; et comme une matrice de rotation commute toujours avec sa transposée, c'est une matrice normale, et elle peut donc être diagonalisée. En conclusion, toute matrice de rotation, exprimée dans une base convenable, se décompose en rotations indépendantes de sous-espaces de dimension 2 (des plans vectoriels); au plus ⁿ⁄₂ d'entre eux.

La somme des termes de la diagonale principale d'une matrice est appelée sa trace ; elle ne dépend pas de la base, et vaut toujours la somme des valeurs propres. Cela a l'intéressante conséquence pratique de donner directement l'angle de rotation θ (dans un (sous)-espace de dimension 2) pour les matrices de rotation 2×2 et 3×3 : pour une matrice 2×2 la trace est 2 cos(θ) (ce qui est en fait évident, comme on va le voir), et pour une matrice 3×3, elle vaut 1+2 cos(θ). En dimension 3, le sous-espace est formé des vecteurs orthogonaux à l'axe de rotation (la direction propre de valeur propre 1). Ainsi, à partir de n'importe quelle matrice de rotation 3×3, on peut déterminer un axe et un angle, et ceux-ci déterminent complètement la rotation (à l'orientation près).

Suites d'angles

Une matrice de rotation 2×2 a nécessairement la forme suivante :

$Q={\begin{pmatrix}a&-b\\b&a\end{pmatrix}}$

avec a²+b² = 1. Nous pouvons donc poser a = cos θ et b = sin θ, pour un certain angle θ. Pour déterminer θ, il ne suffit pas de connaître a ou b seulement ; nous devons utiliser les deux nombres pour obtenir le quadrant correct, à l'aide d'une fonction arctangente à deux variables (notée atan2 dans beaucoup de langages de programmation).

Considérons à présent la première colonne d'une matrice de rotation 3×3,

${\begin{pmatrix}a\\b\\c\end{pmatrix}}.$

Bien que a²+b² ne soit pas en général égal à 1, mais à une certaine valeur r² ≤ 1, nous pouvons utiliser une variante du calcul précédent pour obtenir ce qu'on appelle une « rotation de Givens », transformant la colonne en

${\begin{pmatrix}r\\0\\c\end{pmatrix}},$

annulant le coefficient b. Cette rotation agit sur le plan des axes x et y. Nous pouvons ensuite recommencer dans le plan xz, pour annuler c. Opérant sur la matrice entière, ces deux rotations la mettent sous la forme.

$Q_{xz}Q_{xy}Q={\begin{pmatrix}1&0&0\\0&\ast &\ast \\0&\ast &\ast \end{pmatrix}}.$

Nous intéressant à présent à la deuxième colonne, une rotation de Givens dans le plan yz permet d'annuler la valeur z. La matrice complète devient alors

$Q_{yz}Q_{xz}Q_{xy}Q={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}},$

c'est-à-dire la matrice identité. Ainsi, nous avons décomposé Q en

$Q=Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1}.$

Une matrice de rotation n×n aura (n−1)+(n−2)+⋯+2+1 = n(n-1)/2 termes en dessous de la diagonale qui devront être annulés. Cela peut se faire en généralisant la même idée, parcourant les colonnes avec une série de rotations dans une succession de plans. On en déduit que l'ensemble des matrices de rotation n×n, qui ont chacune n² termes, peut être paramétré par n(n−1)/2 angles.

xzxw	xzyw	xyxw	xyzw
yxyw	yxzw	yzyw	yzxw
zyzw	zyxw	zxzw	zxyw
xzxb	yzxb	xyxb	zyxb
yxyb	zxyb	yzyb	xzyb
zyzb	xyzb	zxzb	yxzb

En trois dimensions, cela reformule dans le langage des matrices une observation faite par Euler, aussi les mathématiciens appellent-ils les trois angles obtenus des angles d'Euler. Cependant, la situation est un peu plus compliquée que ce que nous avons vu jusqu'ici : en dépit du petit nombre de dimensions, nous avons un choix considérable de séquences de paires d'axes, et aussi une certaine liberté dans le choix des angles. Ainsi, de nombreuses conventions différentes sont employées pour paramétrer les rotations tridimensionnelles en physique, en médecine, en chimie, ou dans d'autres disciplines. En tenant compte de la possibilité de prendre des repères fixes ou mobiles, 24 séquences différentes sont possibles. Et alors que certaines disciplines appellent toutes ces séquences des angles d'Euler, d'autres donnent des noms différents (Euler, Cardan, Tait-Byan, lacet-roulis-tangage) à des séquences différentes.

Une des raisons de ce grand nombre d'options est que, comme remarqué précédemment, les rotations en trois dimensions (et plus) ne commutent pas. Si nous permutons une suite donnée de rotations, nous n'obtenons pas (en général) le même résultat. Cela a également pour conséquence que nous ne pouvons pas composer des rotations (d'axes distincts) en additionnant leurs angles. Ainsi, les angles d'Euler ne sont pas des vecteurs, en dépit d'une ressemblance superficielle en tant que triplets de nombres.

Dimensions emboîtées

Une matrice de rotation 3×3 telle que

$Q_{3\times 3}={\begin{pmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{pmatrix}}$

donne l'impression qu'une matrice de rotation 2×2,

$Q_{2\times 2}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}},$

est inscrite dans le coin supérieur gauche :

$Q_{3\times 3}={\begin{pmatrix}Q_{2\times 2}&\mathbf {0} \\\mathbf {0} ^{t}&1\end{pmatrix}}.$

Ce n'est pas une illusion ; on trouve de nombreuses copies de rotations n-dimensionnelles au sein des rotations (n+1)-dimensionnelles, en tant que sous-groupes. Chaque plongement laisse une direction fixe, qui dans le cas des matrices 3×3 est l'axe de rotation. Par exemple, nous avons

$Q_{\mathbf {x} }(\theta )={\begin{pmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\0&\sin \theta &\cos \theta \end{pmatrix}},\qquad Q_{\mathbf {y} }(\theta )={\begin{pmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0&\cos \theta \end{pmatrix}},\qquad Q_{\mathbf {z} }(\theta )={\begin{pmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}},$

fixant respectivement l'axe des x, l'axe des y et l'axe des z. L'axe de rotation n'a pas besoin d'être un axe de coordonnées ; si u = (x, y, z) est un vecteur unité de la direction souhaitée, alors

${\begin{aligned}Q_{\mathbf {u} }(\theta )&{}={\begin{pmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{pmatrix}}\sin \theta +(I-\mathbf {u} \mathbf {u} ^{t})\cos \theta +\mathbf {u} \mathbf {u} ^{t}\\&{}={\begin{pmatrix}(1-x^{2})c_{\theta }+x^{2}&-zs_{\theta }-xyc_{\theta }+xy&ys_{\theta }-xzc_{\theta }+xz\\zs_{\theta }-xyc_{\theta }+xy&(1-y^{2})c_{\theta }+y^{2}&-xs_{\theta }-yzc_{\theta }+yz\\-ys_{\theta }-xzc_{\theta }+xz&xs_{\theta }-yzc_{\theta }+yz&(1-z^{2})c_{\theta }+z^{2}\end{pmatrix}}\\&{}={\begin{pmatrix}x^{2}(1-c_{\theta })+c_{\theta }&xy(1-c_{\theta })-zs_{\theta }&xz(1-c_{\theta })+ys_{\theta }\\xy(1-c_{\theta })+zs_{\theta }&y^{2}(1-c_{\theta })+c_{\theta }&yz(1-c_{\theta })-xs_{\theta }\\xz(1-c_{\theta })-ys_{\theta }&yz(1-c_{\theta })+xs_{\theta }&z^{2}(1-c_{\theta })+c_{\theta }\end{pmatrix}},\end{aligned}}$

où c_θ = cos θ, s_θ = sin θ, est une rotation d'angle θ laissant l'axe u fixé.

Une direction dans l'espace à (n+1) dimensions sera un vecteur unité, que l'on peut considérer comme un point sur une sphère généralisée, Sⁿ. Il est ainsi naturel de décrire le groupe des rotations SO(n+1) comme composé de SO(n) et de Sⁿ. Un formalisme adapté est celui des espaces fibrés,

$SO(n)\hookrightarrow SO(n+1)\to S^{n},\,\!$

où pour chaque direction dans l'« espace de base », Sⁿ, la « fibre » au-dessus d'elle dans l'« espace total », SO(n+1), est une copie de SO(n), représentant les rotations qui gardent cette direction fixée.

Nous pouvons ainsi construire une matrice de rotation n×n en partant d'une matrice 2×2, plaçant un axe de rotation sur S² (la sphère ordinaire de l'espace à trois dimensions), orientant la rotation résultante en ajoutant un axe de rotation sur S³, et ainsi de suite jusqu'à Sⁿ⁻¹. Un point sur Sⁿ possède n « coordonnées sphériques » (en d'autres termes, Sⁿ est une variété de dimension n), ainsi nous avons à nouveau besoin de n(n−1)/2 nombres pour décrire toutes les matrices de rotation n×n.

En fait, la décomposition angulaire séquentielle discutée précédemment peut être vue comme le même processus dans l'autre sens. La composition des n−1 rotations de Givens amène la première colonne (et la première ligne) à (1,0,…, 0), et le reste de la matrice est une matrice de rotation ayant une dimension de moins, plongée de telle sorte que (1,0,…, 0) reste fixé.

Paramétrages antisymétriques

Quand Q, une matrice de rotation n×n, n'admet pas −1 comme valeur propre, et donc qu'aucune des rotations planes qui la composent n'est une rotation de 180°, Q+I est une matrice inversible. C'est le cas de presque toutes les matrices de rotation, et on peut alors montrer que (Q−I)(Q+I)⁻¹ est une matrice antisymétrique, A. Ainsi, A^T = −A; comme la diagonale de A est nécessairement nulle, et que les termes du triangle supérieur déterminent les autres, A contient n(n−1)/2 coefficients indépendants. Heureusement, I−A est inversible si A est antisymétrique ; ainsi nous pouvons retrouver la matrice initiale Q à l'aide de la transformation de Cayley :

$A\mapsto Q=(I+A)(I-A)^{-1},\,\!$

qui envoie n'importe quelle matrice antisymétrique A vers une matrice de rotation. En fait, en dehors des exceptions déjà mentionnées, on peut produire n'importe quelle matrice de rotation de cette manière. Bien que pour des applications pratiques, on puisse rarement se permettre de négliger le cas des rotations de 180°, la transformation de Cayley reste un outil utile, donnant une paramétrisation n'utilisant pas les fonctions trigonométriques de la plupart des matrices de rotation.

En trois dimensions, par exemple, nous avons

${\begin{aligned}&{\begin{pmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{pmatrix}}\mapsto {}\quad {\frac {1}{1+x^{2}+y^{2}+z^{2}}}{\begin{pmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}\end{pmatrix}}.\end{aligned}}$

Si nous notons les termes antisymétriques comme un vecteur, v= (x, y, z), ceci construit une rotation de 90° autour de l'axe des x pour v=(1,0,0), autour de l'axe des y pour v=(0,1,0), et autour de l'axe des z pour v=(0,0,1). Les rotations de 180° sont tout juste inatteignables, car, à la limite quand x tend vers l'infini, la matrice correspondant à v=(x, 0,0) tend vers une rotation de 180° autour de l'axe des x, et il en va de même dans les autres directions.

Topologie du groupe des rotations : théorie de Lie

Groupes de Lie

On a vu que les matrices de rotation n×n forment un groupe, le groupe spécial orthogonal, SO(n). Cette structure algébrique se double d'une structure topologique, car les opérations de multiplication et d'inversion (qui ici est simplement la transposition) sont des fonctions continues des coefficients des matrices. Ainsi SO(n) est un exemple classique de groupe topologique (d'un point de vue purement topologique, c'est une variété compacte). De plus, les opérations sont non seulement continues, mais lisses (de classe ${\mathcal {C}}^{\infty }$), ainsi SO(n) est une variété différentiable et un groupe de Lie.

La plupart des propriétés des matrices de rotation dépendent fort peu de la dimension n; mais envisagé comme un groupe de Lie, on rencontre une différence systématique entre les dimensions paires et impaires. De plus, pour les petites valeurs de n, certaines irrégularités se produisent ; par exemple, contrairement au cas général, SO(4) n'est pas un groupe de Lie simple, mais est isomorphe au produit direct de S³ et de SO(3).

Algèbres de Lie

Associée à chaque groupe de Lie, on définit une algèbre de Lie, un espace vectoriel muni d'une forme bilinéaire alternée appelée un crochet (de Lie). L'algèbre correspondant à SO(n) est notée ${\mathfrak {so}}(n)$ et est formée de toutes les matrices antisymétriques n×n (comme on le voit en dérivant la condition d'orthogonalité, I = Q^TQ). Le crochet de deux matrices antisymétriques est défini par [A₁, A₂] = A₁A₂−A₂A₁, ce qui est encore une matrice antisymétrique. Ce crochet représente l'essence de la structure du groupe de Lie par l'intermédiaire d'infinitésimaux.

Pour les matrices de rotation 2×2, l'algèbre de Lie est une droite vectorielle, formée des multiples de

$J={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}.$

Dans ce cas, le crochet est toujours nul, ce qui nous dit qu'en dimension 2, les rotations commutent. Ce n'est pas le cas en dimensions supérieures. Ainsi, pour les matrices de rotation 3×3, nous obtenons un espace de dimension 3 pour lequel une base commode (de générateurs) est

$A_{\mathbf {x} }={\begin{pmatrix}0&0&0\\0&0&-1\\0&1&0\end{pmatrix}},\quad A_{\mathbf {y} }={\begin{pmatrix}0&0&1\\0&0&0\\-1&0&0\end{pmatrix}},\quad A_{\mathbf {z} }={\begin{pmatrix}0&-1&0\\1&0&0\\0&0&0\end{pmatrix}}.$

Le crochet étant

$A_{\mathbf {x} }A_{\mathbf {y} }=A_{\mathbf {z} },\quad A_{\mathbf {z} }A_{\mathbf {x} }=A_{\mathbf {y} },\quad A_{\mathbf {y} }A_{\mathbf {z} }=A_{\mathbf {x} }.$

On peut naturellement identifier chaque matrice de cette algèbre de Lie avec un vecteur de R³,

${\begin{aligned}{\boldsymbol {\omega }}&{}=(x,y,z)\\{\tilde {\boldsymbol {\omega }}}&{}=xA_{\mathbf {x} }+yA_{\mathbf {y} }+zA_{\mathbf {z} }\\&{}={\begin{pmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{pmatrix}}.\end{aligned}}$

Avec cette identification, le crochet de SO(3) s'identifie au produit vectoriel,

$[{\tilde {\mathbf {u} }},{\tilde {\mathbf {v} }}]=(\mathbf {u} \wedge \mathbf {v} )^{\sim }.\,\!$

De même, la correspondance entre une matrice et le vecteur v qui la représente correspond à

${\tilde {\mathbf {v} }}\mathbf {u} =\mathbf {v} \wedge \mathbf {u} \,\!$,

ce qui implique que v est dans le noyau de l'endomorphisme associé à la matrice avec laquelle on l'a identifié, puisque v$\wedge$v est toujours le vecteur nul.

L'application exponentielle

L'application exponentielle relie l'algèbre de Lie au groupe de Lie ; on la définit à l'aide de la série entière bien connue pour e^x:

${\begin{aligned}\exp \colon {\mathfrak {so}}(n)&{}\to SO(n)\\A&{}\mapsto I+A+{\tfrac {1}{2}}A^{2}+{\tfrac {1}{6}}A^{3}+\cdots +{\tfrac {1}{k!}}A^{k}+\cdots =\sum _{k=0}^{\infty }{\frac {1}{k!}}A^{k}\end{aligned}}$

Pour toute matrice antisymétrique A, exp(A) est toujours une matrice de rotation.

Un important exemple pratique est le cas 3×3, où nous venons de voir qu'on peut identifier chaque matrice antisymétrique avec un vecteur ω = uθ, où u = (x, y, z) est un vecteur unitaire. Rappelons que u est dans le noyau de la matrice associée à ω, et donc que si l'on utilise une base dont u est l'axe des z, la dernière ligne et la dernière colonne seront nulles. Nous savons ainsi déjà que la matrice exponentielle laisse u fixé. Il n'est pas réellement possible de donner une formule pour une telle base en fonction de u (l'existence d'une formule continue contredirait le théorème de la boule chevelue), mais on peut exponentier directement dans la base initiale, obtenant

${\begin{aligned}\exp({\tilde {\boldsymbol {\omega }}})&{}=\exp \left({\begin{pmatrix}0&-z\theta &y\theta \\z\theta &0&-x\theta \\-y\theta &x\theta &0\end{pmatrix}}\right)\\&{}={\begin{pmatrix}2(x^{2}-1)s^{2}+1&2xys^{2}-2zcs&2xzs^{2}+2ycs\\2xys^{2}+2zcs&2(y^{2}-1)s^{2}+1&2yzs^{2}-2xcs\\2xzs^{2}-2ycs&2yzs^{2}+2xcs&2(z^{2}-1)s^{2}+1\end{pmatrix}},\end{aligned}}$

où c = cos ^θ⁄₂, s = sin ^θ⁄₂. On reconnait la matrice d'une rotation d'angle θ autour de l'axe u. Il faut remarquer également que cette transformation de matrices antisymétriques est tout à fait distincte de la transformation de Cayley discutée plus haut.

Quelle que soit la dimension, si nous choisissons une matrice non nulle A et considérons ses multiples (tA, où t est un scalaire), l'exponentiation donne une famille de matrices de rotation e^tA situées le long d'une géodésique du groupe de Lie (en tant que variété), formant un sous-groupe à un paramètre. Plus généralement, l'exponentielle est un homéomorphisme entre un voisinage de 0 dans l'algèbre de Lie et un voisinage de l'identité du groupe de Lie. En fait, on peut construire n'importe quelle matrice de rotation comme exponentielle d'une matrice antisymétrique, donc pour ces groupes l'application exponentielle est une surjection.

La formule de Baker–Campbell–Hausdorff

Soient deux matrices A et B de l'algèbre de Lie. Leurs exponentielles, exp(A) et exp(B), sont des matrices de rotation, que nous pouvons multiplier. Comme l'application exponentielle est surjective, nous savons qu'il existe C dans l'algèbre de Lie telle que exp(A)exp(B) = exp(C), ce que nous noterons

$A\ast B=C.\,\!$

Quand exp(A) et exp(B) commutent (ce qui est toujours le cas pour les matrices 2×2, mais pas en général en dimension supérieure), on a C =A+B, comme pour l'exponentiation complexe. Le cas général est donné par la formule de Baker-Campbell-Hausdorff (dite formule BCH), un développement en série en termes de crochets, qui pour des matrices sont les commutateurs, détectant le défaut de commutativité de la multiplication. La formule générale est assez complexe, mais dans le cas des matrices, elle se simplifie en

$A\ast B=\sum _{n>0}{\frac {(-1)^{n-1}}{n}}\sum _{\begin{smallmatrix}r_{i}+s_{i}>0\,\\1\leq i\leq n\end{smallmatrix}}{\frac {A^{r_{1}}B^{s_{1}}\cdots A^{r_{n}}B^{s_{n}}}{r_{1}!s_{1}!\cdots r_{n}!s_{n}!}}$, dont les premiers termes peuvent aussi s'écrire

$A\ast B=A+B+{\tfrac {1}{2}}[A,B]+{\tfrac {1}{12}}[A,[A,B]]-{\tfrac {1}{12}}[B,[A,B]]-\cdots \,\!$

La représentation d'une matrice de rotation par sa décomposition angulaire, comme dans le cas des angles d'Euler, peut amener à la tentation de considérer les rotations comme formant un espace vectoriel, mais la présence des termes d'ordre supérieur dans la formule BCH montre que cela serait une erreur.

Revenons au cas 3×3, où [A, B] est égal au produit vectoriel, $A\wedge B$. Si A et B sont linéairement indépendantes, alors A, B, et A$\wedge$B forment une base ; sinon, A et B commutent. Et il s'avère que, en dimension 3, la série de la formule BCH peut se mettre sous la forme "exacte" αA+βB+γA$\wedge$B.

Le groupe Spin

Le groupe de Lie des matrices de rotation n×n, SO(n), est une variété compacte et connexe par arcs. Mais il n'est pas simplement connexe, aussi la théorie de Lie nous dit que c'est l'« ombre » (l'image par une application continue) d'un groupe de revêtement universel. Le groupe de revêtement, qui dans ce cas est le groupe Spin (ou groupe de spins, ou groupe des spineurs), noté Spin(n), est en général plus simple et il est plus naturel de s'y placer.

Dans le cas des rotations planes, SO(2) est topologiquement un cercle, la sphère S¹. Son groupe de revêtement universel, Spin(2), est isomorphe à la droite réelle, R, munie de l'addition. En d'autres termes, chaque fois que nous utilisons des angles de valeur arbitraire, ce que nous faisons souvent, nous profitons de la simplicité des nombres réels, dont les angles sont les « ombres ». Toute matrice de rotation 2×2 correspond à une infinité dénombrable d'angles, séparés par des multiples entiers de 2π ; cela correspond à ce que le groupe fondamental de SO(2) est isomorphe aux entiers relatifs, Z.

Dans le cas des rotations de l'espace, SO(3) est topologiquement équivalent à l'espace projectif réel de dimension 3, P³(R). Son revêtement universel, Spin(3), est isomorphe à la 3-sphère, S³ ; et chaque matrice de rotation 3×3 correspond à deux points opposés de la sphère. Par conséquent, le groupe fondamental de SO(3) est isomorphe au groupe à deux éléments, Z₂. Nous pouvons aussi décrire Spin(3) comme isomorphe au groupe multiplicatif des quaternions de norme 1, ou à un certain ensemble de matrices réelles 4×4, ou de matrices complexes 2×2.

Concrètement, un quaternion unité, q, avec

${\begin{aligned}q&{}=w+\mathbf {i} x+\mathbf {j} y+\mathbf {k} z,\\1&{}=w^{2}+x^{2}+y^{2}+z^{2},\end{aligned}}$

correspond à la matrice de rotation

$Q={\begin{pmatrix}2x^{2}+2w^{2}-1&2xy-2zw&2xz+2yw\\2xy+2zw&2y^{2}+2w^{2}-1&2yz-2xw\\2xz-2yw&2yz+2xw&2z^{2}+2w^{2}-1\end{pmatrix}}.$

C'est notre troisième version de cette matrice, ici représentant une rotation d'angle 2θ autour du vecteur non-unitaire (x, y, z), où cos θ = w et |sin θ| = ||(x, y, z)|| (le signe de sin θ dépend des signes des composantes de l'axe).

En dimension supérieure, beaucoup des propriétés de ce cas se généralisent. Les recouvrements ont tous une fibre de deux éléments, et SO(n), n > 2, a toujours pour groupe fondamental Z₂. Le cadre naturel pour étudier ces groupes est celui des algèbres de Clifford. Et l'action des rotations est donnée par une sorte de "sandwich", noté qvq^∗.

Rotations infinitésimales

Les matrices de l'algèbre de Lie ne sont pas elles-mêmes des rotations ; ces matrices antisymétriques sont des dérivées, proportionnelles à des différences de rotations. Une véritable "rotation différentielle", ou encore une matrice de rotation infinitésimale a la forme

$I+A\,d\theta ,\,\!$

où dθ est infiniment petit. Ces matrices n'ont pas toutes les propriétés des matrices de rotation (finies) usuelles. Pour le comprendre, considérons

$dA_{\mathbf {x} }={\begin{pmatrix}1&0&0\\0&1&-d\theta \\0&d\theta &1\end{pmatrix}}.$

La condition d'orthogonalité, Q^tQ = I n'est pas vérifiée, puisque le produit

$dA_{\mathbf {x} }^{t}\,dA_{\mathbf {x} }={\begin{pmatrix}1&0&0\\0&1+d\theta ^{2}&0\\0&0&1+d\theta ^{2}\end{pmatrix}},$

diffère de la matrice identité par des infiniment petits du second ordre ; nous les négligeons donc, et nous dirons qu'au premier ordre, une matrice infinitésimale de rotation est orthogonale. Regardons à présent le carré de la matrice

$dA_{\mathbf {x} }^{2}={\begin{pmatrix}1&0&0\\0&1-d\theta ^{2}&-2d\theta \\0&2d\theta &1-d\theta ^{2}\end{pmatrix}}$

Négligeant à nouveau les termes du second ordre, nous voyons que l'angle a simplement doublé. La différence principale de comportement, nous demandera une seconde rotation infinitésimale,

$dA_{\mathbf {y} }={\begin{pmatrix}1&0&d\phi \\0&1&0\\-d\phi &0&1\end{pmatrix}}.$

Comparons les produits dA_xdA_y et dA_ydA_x.

${\begin{aligned}dA_{\mathbf {x} }\,dA_{\mathbf {y} }&{}={\begin{pmatrix}1&0&d\phi \\d\theta \,d\phi &1&-d\theta \\-d\phi &d\theta &1\end{pmatrix}}\\dA_{\mathbf {y} }\,dA_{\mathbf {x} }&{}={\begin{pmatrix}1&d\theta \,d\phi &d\phi \\0&1&-d\theta \\-d\phi &d\theta &1\end{pmatrix}}\\\end{aligned}}$

Comme $d\theta \ d\phi$ est du second ordre, nous le négligeons; ainsi, au premier ordre, la multiplication des matrices de rotation infinitésimales est commutative. En fait,

$dA_{\mathbf {x} }\,dA_{\mathbf {y} }=dA_{\mathbf {y} }\,dA_{\mathbf {x} },\,\!$

toujours au premier ordre.

Il faut donc toujours soigneusement distinguer (le traitement au premier ordre de) ces matrices infinitésimales à la fois des matrices de rotation finies, et des dérivées de ces matrices (qui sont antisymétriques). Ainsi, le comportement des matrices finies dans la formule BCH contraste avec celui des matrices infinitésimales, car tous les termes des commutateurs seront des infiniment petits du second ordre, et donc ces matrices formeront bien un espace vectoriel dans ce cas.

Conversions

Nous avons vu l'existence de plusieurs décompositions et constructions progressives s'appliquant en toutes dimensions. Nous allons à présent nous intéresser de plus près au cas des rotations en dimension 3.

Quaternions

Réécrivons à nouveau la matrice générale de rotation 3×3 sous la forme

$Q={\begin{pmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{pmatrix}}.$

À présent, chaque composante d'un quaternion apparaît (doublée) dans un terme de degré 2, et si tous ces termes sont nuls, nous obtenons une matrice identité. Ceci permet une conversion efficace et robuste d'un quaternion quelconque (unitaire ou non, et même nul) vers une matrice de rotation 3×3.

Puisqu'il n'est plus nécessaire que les quaternions utilisés soient unitaires, nous pouvons utiliser les quaternions non nuls comme des coordonnées homogènes pour les matrices de rotation 3×3. La transformation de Cayley discutée plus haut est obtenue en divisant le quaternion par sa composante en w. Pour une rotation de 180° autour d'un axe, w sera nul, ce qui explique la limitation de Cayley.

La somme des termes de la diagonale principale (la trace), vaut 3−4(x²+y²+z²), c'est-à-dire 2w²+2w²-1. On voit que les termes de la diagonale ont tous la même forme : 2x²+2w²−1, 2y²+2w²−1, et 2z²+2w²−1.

La diagonale de la matrice permet ainsi de comparer les valeurs absolues des quatre composantes du quaternion ; nous pouvons en fait les obtenir en n'utilisant que des sommes et des racines carrées, et déterminer les signes à l'aide des coefficients (antisymétriques) hors de la diagonale.

Exemples de ces calculs

w = 0.5*sqrt(1+Qxx+Qyy+Qzz)
x = copysign(0.5*sqrt(1+Qxx-Qyy-Qzz),Qzy-Qyz)
y = copysign(0.5*sqrt(1-Qxx+Qyy-Qzz),Qxz-Qzx)
z = copysign(0.5*sqrt(1-Qxx-Qyy+Qzz),Qyx-Qxy)

où copysign(x,y) est x avec le signe de y:

copysign(x,y)$={\frac {|x|}{|y|}}\,y$

Ou encore, en n'utilisant qu'une racine carrée et une division :

t = Qxx+Qyy+Qzz
r = sqrt(1+t)
s = 0.5/r
w = 0.5*r
x = (Qzy-Qyz)*s
y = (Qxz-Qzx)*s
z = (Qyx-Qxy)*s

Ceci est numériquement stable tant que la trace, t, n'est pas négative, sinon on risque une division par zéro (ou un nombre très petit).

Supposons alors que Q_xx soit le plus grand terme de la diagonale, et donc que x ait la plus grande valeur absolue (les autres cas sont analogues) ; alors ce qui suit est sans risque :

r = sqrt(1+Qxx-Qyy-Qzz)
s = 0.5/r
w = (Qzy-Qyz)*s
x = 0.5*r
y = (Qxy+Qyx)*s
z = (Qzx+Qxz)*s

Si la matrice n'est pas connue exactement (par exemple à la suite d'approximations numériques successives), nous pouvons construire une matrice symétrique 4×4,

$K={\frac {1}{3}}{\begin{pmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{yz}-Q_{zy}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{zx}-Q_{xz}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{xy}-Q_{yx}\\Q_{yz}-Q_{zy}&Q_{zx}-Q_{xz}&Q_{xy}-Q_{yx}&Q_{xx}+Q_{yy}+Q_{zz}\end{pmatrix}},$

et chercher le vecteur propre, (x,y,z,w), correspondant à sa plus grande valeur propre (en valeur absolue) ; si Q est vraiment une matrice de rotation, cette valeur propre vaudra 1. Le quaternion ainsi obtenu correspondra à la matrice de rotation la plus proche de la matrice initiale.

Décomposition polaire

Si M, une matrice n×n, est régulière, ses colonnes forment une base, que le procédé d'orthogonalisation de Schmidt permet de transformer en une base orthonormale. En termes d'algèbre linéaire numérique (en), nous transformons M en une matrice orthogonale Q, à l'aide de la décomposition QR. Cependant, on préfèrerait souvent obtenir la matrice Q « la plus proche » de M, ce que cette méthode échoue à faire ; l'outil approprié pour cela est la décomposition polaire.

Pour mesurer la proximité des matrices, nous pouvons utiliser n'importe quelle norme invariante par transformations orthogonales. Un choix approprié est celui de la norme de Frobenius, ||Q−M||_F, la racine carrée de la somme des carrés des différences des termes de Q et de M. Exprimé en termes de la trace Tr, notre but est de

• Trouver Q minimisant Tr( (Q−M)^t(Q−M) ), sous la contrainte Q^tQ = I.

Bien qu'écrite en termes matriciels, la fonction d'optimisation est simplement un polynôme quadratique. Nous pouvons le minimiser simplement en cherchant où sa dérivée s'annule. Pour une matrice 3×3, la condition d'orthogonalité entraîne six égalités (scalaires) que doivent satisfaire les coefficients de Q. Pour y ajouter les contraintes, on peut employer la méthode standard des multiplicateurs de Lagrange, formant ici une matrice symétrique Y. Ainsi, notre méthode consiste à :

• Dériver Tr( (Q−M)^t(Q−M) + (Q^tQ−I)Y ) par rapport aux termes de Q, et chercher où ces dérivées partielles s'annulent.

Un exemple de ces calculs

Considérons un exemple 2×2. Avec les contraintes, nous cherchons à minimiser

${\begin{aligned}&\scriptstyle {(Q_{xx}-M_{xx})^{2}+(Q_{xy}-M_{xy})^{2}}\\&\scriptstyle {{}+(Q_{yx}-M_{yx})^{2}+(Q_{yy}-M_{yy})^{2}}\\&\scriptstyle {{}+(Q_{xx}^{2}+Q_{yx}^{2}-1)Y_{xx}+(Q_{xy}^{2}+Q_{yy}^{2}-1)Y_{yy}}\\&\scriptstyle {{}+2(Q_{xx}Q_{xy}+Q_{yx}Q_{yy})Y_{xy}.}\end{aligned}}$

Prenant successivement les dérivées par rapport à Q_xx, Q_xy, Q_yx et Q_yy, nous formons une matrice.

$\scriptstyle {2{\begin{pmatrix}\scriptstyle {Q_{xx}-M_{xx}+Q_{xx}Y_{xx}+Q_{xy}Y_{xy}}&\scriptstyle {Q_{xy}-M_{xy}+Q_{xx}Y_{xy}+Q_{xy}Y_{yy}}\\\scriptstyle {Q_{yx}-M_{yx}+Q_{yx}Y_{xx}+Q_{yy}Y_{xy}}&\scriptstyle {Q_{yy}-M_{yy}+Q_{yx}Y_{xy}+Q_{yy}Y_{yy}}\end{pmatrix}}}$

En général, nous obtenons l'équation

$0=2(Q-M)+2QY,\,\!$

et donc

$M=Q(I+Y)=QS,\,\!$

où Q est orthogonale et S est symétrique. Pour assurer un minimum, la matrice Y (et donc aussi S) doit être définie positive. QS s'appelle la décomposition polaire de M, où S est la racine carrée positive de S² = M^tM.

$S^{2}=(Q^{t}M)^{t}(Q^{t}M)=M^{t}QQ^{t}M=M^{t}M\,\!$

Quand M est inversible, les facteurs Q et S de la décomposition polaire sont uniques. Cependant, le déterminant de S est positif, car S est définie positive, ainsi Q est du signe du déterminant de M. Ainsi, Q est seulement garantie orthogonale, et non une matrice de rotation. Ceci est inévitable ; on ne peut définir (avec unicité) une matrice de rotation la plus proche d'une matrice M de déterminant négatif.

Axe et angle de rotation

Pour construire efficacement une matrice de rotation à partir d'un angle θ et d'un vecteur axial unitaire u, nous pouvons utiliser les symétries (et antisymétries) entre les termes :

c = cos(θ); s = sin(θ); C = 1-c
xs = x*s;   ys = y*s;   zs = z*s
xC = x*C;   yC = y*C;   zC = z*C
xyC = x*yC; yzC = y*zC; zxC = z*xC
[ x*xC+c   xyC-zs   zxC+ys ]
[ xyC+zs   y*yC+c   yzC-xs ]
[ zxC-ys   yzC+xs   z*zC+c ]

Déterminer un axe et un angle, comme déterminer un quaternion, n'est possible qu'au signe près ; en effet, (u,θ) et (−u,−θ) correspondent à la même matrice de rotation, tout comme q et −q. Mais cette détermination présente des difficultés supplémentaires : l'angle peut être restreint à l'intervalle entre 0° et 180°, mais les angles ne sont définis qu'à 360° près. De plus, quand l'angle est nul, l'axe n'est pas défini; quand l'angle est 180°, la matrice devient symétrique, ce qui rend difficile la détermination de l'axe. Ainsi, près des multiples de 180°, il faut prêter beaucoup d'attention aux incertitudes numériques : en déterminant l'angle, une fonction arctangente à deux variables (avec atan2(sin θ,cos θ) égal à θ) est nécessaire pour éviter l'insensibilité de arccos ; de même, en calculant la norme d'un vecteur de l'axe (pour construire un vecteur unitaire) une approche en force brute peut perdre trop de précision. On peut souvent utiliser

x = Qzy-Qyz
y = Qxz-Qzx
z = Qyx-Qxy
r = hypot(x,hypot(y,z))
t = Qxx+Qyy+Qzz
θ = atan2(r,t−1)

Les composants x, y, et z de l'axe doivent ensuite être divisés par r. Comme pour la représentation par quaternions, des formules différentes doivent être utilisées quand t est négatif ; enfin, quand r est nul (parce que l'angle est nul), un axe doit être fourni arbitrairement.

Angles d'Euler

La complexité de la conversion est plus grande dans le cas des angles d'Euler (ici envisagés dans le sens le plus général). La première difficulté est de déterminer quel ordre d'axes cartésiens utiliser (parmi les 24 possibles). Supposons que les trois angles soient θ₁, θ₂, θ₃ ; les physiciens et les chimistes peuvent les interpréter comme

$Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{1})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {z} }(\theta _{3}),\,\!$

alors que les aérodynamiciens utiliseront

$Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{3})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {x} }(\theta _{1}).\,\!$

Une approche systématique commence par choisir l'axe le plus à droite. Parmi toutes les permutations de (x,y,z), deux seulement placent cet axe en premier ; l'une est paire et l'autre impaire. Le choix de la parité permet ainsi de déterminer l'axe du milieu, laissant deux choix pour l'axe le plus à gauche, répétant ou non le premier choix. Ceci donne 3×2×2 = 12 variations ; choisissant des axes fixes ou mobiles, on aboutit à 24 possibilités.

Cela suffit à construire une matrice à partir des angles, mais de nombreux triplets différents peuvent donner la même matrice. Ainsi, si nous utilisons la convention zyz choisie plus haut, nous avons les paires équivalentes suivantes :

(90°,	45°,	−105°)	≡	(−270°,	−315°,	255°)	multiples de 360°
(72°,	0°,	0°)	≡	(40°,	0°,	32°)	alignement singulier
(45°,	60°,	−30°)	≡	(−135°,	−60°,	150°)	bascule bistable

Le problème de l'alignement singulier, l'analogue mathématique du phénomène physique de blocage de cardan (gimbal lock) se produit lorsque la rotation intermédiaire aligne les axes des deux autres rotations. Ces singularités ne sont pas caractéristiques de la matrice de rotation elle-même, et ne se produisent que lors de l'utilisation des angles d'Euler.

Pour les éviter, il faut manipuler la matrice en tant que famille de vecteurs-colonnes (ou lignes) orthonormale (appelés souvent, dans les applications 3D, vecteurs "droit", "haut" et "extérieur"); elles ne se produisent également pas lorsqu'on utilise les quaternions.

Matrices de rotation aléatoires

Il est parfois nécessaire de construire une matrice de rotation aléatoire (avec une distribution uniforme). Intuitivement, il semble clair en dimension 2 que cela implique que l'angle de rotation soit uniformément distribué entre 0 et 2π. Cette intuition est correcte, mais ne s'étend pas aux dimensions supérieures. Ainsi, si nous considérons les matrices de rotation 3×3 sous la forme axe-angle, l'angle ne doit pas être uniformément distribué ; la probabilité que la mesure de l'angle soit au plus θ devrait être¹⁄_π(θ − sin θ), pour 0 ≤ θ ≤ π.

Comme SO(n) est un groupe de Lie connexe et localement compact, nous avons un critère simple de distribution uniforme, à savoir que la distribution soit invariante par rotation (les "translations" du groupe) ; cette définition correspond à la mesure de Haar. Il est possible d'utiliser la transformation de Cayley pour engendrer et tester des matrices selon ce critère.

On peut également engendrer une distribution uniforme en toute dimension à l'aide de l'algorithme du sous-groupe de Diaconis et Shashani, lequel exploite récursivement la structure des groupes emboîtés de SO(n), de la manière suivante : engendrer un angle au hasard entre 0 et 2π et construire la matrice de rotation 2×2 correspondante. Pour passer de n à n+1, engendrer un vecteur v uniformément distribué sur la n-sphère, Sⁿ, prolonger la n×n matrice en ajoutant comme dernière colonne et dernière ligne (0,…,0,1), et composer par une rotation cette nouvelle matrice pour que la dernière colonne devienne v.

Comme d'habitude, des méthodes plus spécialisées existent pour le cas 3×3. Dans chaque cas, on commence par choisir trois nombres indépendants uniformément distribués entre 0 et 1. Arvo part d'une transformation de Householder et exploite la dimension impaire pour en tirer une rotation en la multipliant par -1, puis pour déterminer l'axe d'une rotation uniformément distribuée.

Une autre méthode part de quaternions de norme 1. La multiplication des matrices est homéomorphe à celle des quaternions, et multiplier par un quaternion unitaire revient à faire tourner la sphère unité. Comme cet homéomorphisme est localement une isométrie, on en conclut qu'on obtiendra une distribution uniforme sur SO(3) en partant d'une distribution uniforme sur S³.

Il est également possible d'utiliser les angles d'Euler, mais avec une distribution non uniforme.

Enfin, sous la forme axe-angle, l'axe doit être uniformément distribué, mais l'angle de rotation a la distribution non-uniforme notée précédemment.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Rotation matrix » (voir la liste des auteurs).

Voir aussi

Articles connexes

• Rotation vectorielle
• Rotation affine
• Isométrie
• Rotation plane
• Rotation dans l'espace
• Matrice orthogonale
• Système roulis-tangage-lacet
• Représentation d'une rotation (en)
• Quaternions et rotation dans l'espace

Liens externes

• (en) Eric W. Weisstein, « Rotation Matrix », sur MathWorld
• (en) Math Awareness Month 2000 interactive demo (requires Java)
• (en) Rotation Matrices at MathPages
• (fr) Application interactive illustrant la rotation matricielle 3D appliquée à une image SVG