Théorie des catégories
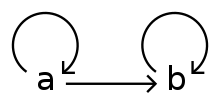
La théorie des catégories est l'étude des structures mathématiques et de leurs relations. Ce domaine rend compte de l'abondance de caractéristiques partagées par diverses classes liées à des structures mathématiques. Les catégories sont utilisées dans plusieurs branches des mathématiques et dans certains secteurs de l'informatique théorique et de la physique théorique. Elles forment une notion unificatrice. « La théorie des catégories commence avec l'observation que de nombreuses propriétés des systèmes mathématiques peuvent être unifiées et simplifiées par des dessins avec des flèches[1]. »
Histoire[modifier | modifier le code]
Cette théorie a été mise en place par Samuel Eilenberg et Saunders Mac Lane en 1942-1945, en lien avec la topologie algébrique, et propagée dans les années 1960-1970 en France par Alexandre Grothendieck, qui en a fait une étude systématique. À la suite des travaux de William Lawvere, la théorie des catégories est utilisée depuis 1969 pour définir la logique et la théorie des ensembles ; la théorie des catégories peut donc, comme la théorie des ensembles ou la théorie des types, avec laquelle elle a des similarités, être considérée comme fondement des mathématiques[2].
Éléments de base[modifier | modifier le code]
Morphismes[modifier | modifier le code]
Voici un exemple. La classe Grp des groupes comprend tous les objets ayant une « structure de groupe ». Plus précisément, Grp comprend tous les ensembles G munis d'une opération interne qui satisfait les axiomes d'associativité, inversibilité et de l'élément neutre. Des théorèmes peuvent ainsi être prouvés en effectuant des déductions logiques à partir de ces axiomes. Par exemple, ils apportent la preuve directe que l'élément neutre d'un groupe est unique.
Au lieu d'étudier les objets (par exemple les groupes) qui possèdent une structure donnée, comme les théories mathématiques l'ont toujours fait, la théorie des catégories met l'accent sur les morphismes et les processus qui préservent la structure entre deux objets. Il apparaît qu'en étudiant ces morphismes, l'on est capable d'en apprendre plus sur la structure des objets.
Dans notre exemple, les morphismes étudiés sont les morphismes de groupes, à savoir toute application d'un groupe dans un groupe vérifiant : . L'étude des morphismes de groupes fournit un outil pour étudier les propriétés générales des groupes et les conséquences des axiomes relatifs aux groupes.
Il en est de même dans de nombreuses théories mathématiques, où l'on peut définir une classe d'objets ainsi que des applications particulières entre ces objets vérifiant certaines propriétés. Un autre exemple de catégorie est donnée par la classe des espaces vectoriels, les morphismes étant les applications linéaires. Un dernier exemple est donné par la classe des espaces topologiques, les morphismes étant les applications continues. Ainsi, une catégorie est une formulation axiomatique qui relie des structures mathématiques aux fonctions qui les préservent. Une étude systématique des catégories permet de prouver des résultats généraux à partir des axiomes d'une catégorie.
Foncteurs[modifier | modifier le code]
Une catégorie est elle-même un type de structure mathématique. Si l'on dispose de deux catégories et , il est parfois possible de définir une correspondance entre la première catégorie et la deuxième, associant à chaque objet (respectivement chaque morphisme) de la première catégorie un objet (respectivement un morphisme) de la deuxième, tout en préservant la structure de catégorie. De telles correspondances sont appelées foncteurs.
Si l'on se restreint aux petites catégories (c'est-à-dire aux catégories dont les classes d'objets et de morphismes sont des ensembles), on définit ainsi la catégorie des petites catégories Cat : ses objets sont les petites catégories, et ses morphismes sont les foncteurs.
Cette idée fondamentale de relier une classe d'objets à une autre apparut d'abord en topologie algébrique : certains problèmes topologiques complexes peuvent être traduits en questions algébriques, qui sont souvent plus faciles à résoudre. Ainsi, on peut définir un foncteur de la catégorie des espaces topologiques dans la catégorie des groupes, qui, à un espace topologique, associe son groupe fondamental. Toute propriété topologique de la première catégorie pourra se traduire par une propriété algébrique dans la deuxième catégorie et inversement.
Transformations naturelles[modifier | modifier le code]
Par un nouvel effort d'abstraction, les foncteurs sont souvent « reliés naturellement ». C'est pourquoi l'on définit le concept de transformation naturelle, qui est une manière d'envoyer un foncteur sur un foncteur. Alors que le foncteur est un morphisme de catégories, la transformation naturelle est un morphisme de foncteurs (i.e. un morphisme dans une catégorie de foncteurs). On peut ainsi étudier de nombreuses constructions mathématiques. La « naturalité » est un principe plus profond qu'il n'en a l'air au premier regard. Saunders Mac Lane, coinventeur de la théorie des catégories, a ainsi déclaré : « je n'ai pas inventé les catégories pour étudier les foncteurs ; je les ai inventées pour étudier les transformations naturelles ».
Par exemple, il existe un isomorphisme entre un espace vectoriel de dimension finie et son espace dual, mais cet isomorphisme n'est pas « naturel », dans le sens où sa définition requiert d'avoir choisi une base, dont elle dépend étroitement. En revanche, il existe un isomorphisme naturel entre un espace vectoriel de dimension finie et son espace bidual (le dual de son dual), c'est-à-dire en l'occurrence indépendant de la base choisie. Cet exemple est, historiquement, le premier formulé dans l'article fondateur de Samuel Eilenberg et Saunders Mac Lane en 1945.
Autre exemple : il existe plusieurs manières de relier par divers foncteurs les espaces topologiques à la théorie des groupes : homologie, cohomologie, homotopie… L'étude des transformations naturelles permet d'examiner comment ces foncteurs sont eux-mêmes reliés les uns aux autres.
Définitions[modifier | modifier le code]
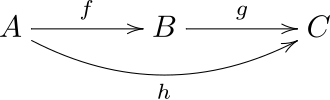

Catégorie[modifier | modifier le code]
Une catégorie , dans le langage de la théorie des classes, est la donnée de six éléments[3] :
- une classe dont les éléments sont appelés objets (les objets de la catégorie) ;
- une classe dont les éléments sont appelés morphismes ou flèches (les morphismes ou les flèches de la catégorie) ;
- deux « applications » de dans (au sens de la théorie des classes, c'est-à-dire que leurs « graphes » peuvent être des classes propres), appelées source et but ; f : A → B signifie que f est un morphisme « de A dans B » (c'est-à-dire de source A et de but B) et la classe de tous ces morphismes f est notée ;
- un morphisme , pour chaque objet , appelé identité de ou flèche unité ou flèche neutre[4];
- une composition qui, à tout couple de morphismes et , associe un morphisme appelé composée de et , et telle que :
- la composition est associative : pour tous morphismes , et , ;
- les identités sont des éléments neutres de la composition : pour tout morphisme ,.
Lorsqu'une catégorie est courante, certains lui donnent comme nom l'abréviation du nom de ses objets ; nous suivrons ici cette convention.
Certains auteurs comme D. E. Rydeheard et Burstall[5] définissent une catégorie comme un graphe orienté (plus précisément un multigraphe). Les sommets du graphe sont les objets, et les flèches sont les morphismes. De même, il arrive parfois que l'on oublie complètement les objets d'une catégorie et que l'on ne s'intéresse plus qu'aux flèches, en identifiant les objets à leurs flèches identités.
Quelques propriétés[modifier | modifier le code]
Une catégorie est dite localement petite si, pour tous objets A, B de , la classe des morphismes de A dans B, i.e. est un ensemble. Une catégorie est petite si la classe de tous les morphismes de , i.e. , est un ensemble[6]. La plupart des catégories usuelles — cf. exemples ci-dessous — sont seulement localement petites.
Une sous-catégorie de est une catégorie dont les objets sont des objets de et dont les flèches sont des flèches (mais pas nécessairement toutes les flèches) de entre deux objets de la sous-catégorie. Lorsqu'une sous-catégorie de est telle que toutes les flèches de entre deux objets de sont des flèches de , cette sous-catégorie est dite pleine. Par exemple, Ab est une sous-catégorie pleine de Gr. La catégorie de tous les espaces métriques avec les isométries n'est pas une sous-catégorie pleine de Top mais celle des espaces séparés en est une[7].
Catégorie duale[modifier | modifier le code]
Étant donné une catégorie , on définit la catégorie opposée ou duale, en prenant les mêmes objets et les mêmes flèches, mais en inversant les fonctions source et but et en remplaçant la composition par son "symétrique". On la note (ou ). Plus précisément : HomCop(A, B) = HomC(B, A), et la composition opposée de deux flèches est le "symétrique" de leur composition : f∘opg = g∘f. Il est clair que la catégorie duale de la catégorie duale est la catégorie de départ : . Cette dualisation permet de symétriser la plupart des énoncés.
Exemples[modifier | modifier le code]
Intuitivement, les objets d'une catégorie sont souvent des ensembles avec une structure, et les flèches sont souvent des applications entre les ensembles qui en préservent la structure. La table suivante donne des exemples de catégories qui illustrent cette intuition[8].
| Catégorie | Objets | Flèches |
|---|---|---|
| catégorie Ens ou Set | ensembles | applications |
| catégorie Top | espaces topologiques | applications continues |
| catégorie Met | espaces métriques | applications uniformément continues |
| catégorie Mon | monoïdes | morphismes de monoïdes |
| catégorie Grp | groupes | morphismes de groupes |
| catégorie Ab | groupes abéliens | morphismes de groupes |
| catégorie ACU | anneaux commutatifs unitaires | morphismes d'anneaux |
| catégorie Ord | ensembles ordonnés | applications croissantes |
On définit également la catégorie des modules à gauche sur un anneau, la catégorie des espaces vectoriels sur un corps donné, la catégorie des ensembles munis d'une tribu, la catégorie des espaces mesurés[4], etc.
Les exemples de la table sont des catégories concrètes, c'est-à-dire des catégories munies d'un foncteur fidèle vers la catégorie des ensembles (dans les cas présents, il s'agit du foncteur d'oubli, qui fait abstraction des structures considérées pour ne retenir que leur ensemble de base ; par exemple, appliquer le foncteur d'oubli au groupe (ℤ, +) donne l'ensemble ℤ). Toute petite catégorie est concrète, comme les deux suivantes :
- On se donne un monoïde M, et on définit la catégorie associée ainsi :
- objets : un seul
- flèches : les éléments du monoïde, elles partent toute de l'unique objet pour y revenir ;
- composition : donnée par la loi du monoïde (l'identité est donc la flèche associée au neutre de M).
- On se donne un ensemble E muni d'une relation réflexive et transitive R (autrement dit, R est une relation de préordre) et on définit la catégorie associée, notée [4], ainsi :
- objets : les éléments de l'ensemble ;
- flèches : pour tous objets e et f, il existe une flèche de e vers f si et seulement si eRf (et pas de flèche sinon) ;
- composition : la composée de deux flèches est la seule flèche qui réunit les deux extrémités (la relation est transitive) ; l'identité est la seule flèche qui relie un objet à lui-même (la relation est réflexive).
- Cet exemple est particulièrement intéressant dans le cas suivant : l'ensemble est l'ensemble des ouverts d'un espace topologique, et la relation est l'inclusion ; cela permet de définir les notions de préfaisceau et de faisceau, via les foncteurs.
- Il permet aussi de considérer tout ensemble ordonné comme une catégorie, et tout système inductif (resp. projectif) comme un foncteur covariant (resp. contravariant) sur cette catégorie.
- Un exemple de catégorie non concrète : la catégorie homotopique (en) hTop, dont les objets sont les espaces topologiques et dont les morphismes sont les classes d'homotopie d'applications continues.
- Étant donné deux catégories et , on peut définir la catégorie produit de la façon suivante : les objets de la catégorie produit sont les couples (A, B) formés d'un objet A de et d'un objet B de ; les morphismes sont les couples (f,g) formés d'un morphisme f de et d'un morphisme g de . La composition de ces couples se fait composante par composante.
- Une catégorie est dite discrète si elle n'a pas d'autres flèches que les flèches neutres, ie si pour tout objet et si pour tout couple d'objets distincts on a . Il est bien évident que toute collection d'objets peut être considérée comme une catégorie discrète.
- Un doublet est une catégorie ayant deux objets, notés par exemple 0 et 1, et seulement deux flèches non neutres, toutes deux de source 0 et de but 1. Un doublet n'a ni objet initial ni objet final.[9]
Exemple en informatique[modifier | modifier le code]
Benjamin C. Pierce , p. 8 dans Basic Category Theory for Computer Scientists, considère un langage de programmation fonctionnelle où les types sont Bool (pour les booléens, c.-à-d. pour les valeurs de vérité), Int (pour les nombres entiers), Real (pour les nombres réels) et Unit (un type avec un seul élément). Les opérations sont iszero : Int → Bool (qui teste si un nombre entier vaut zero), not : Bool → Bool (négation), succInt : Int → Int (qui renvoie le successeur d'un nombre entier), succReal : Real → Real, (qui renvoie le successeur d'un nombre réel), toReal : Int → Real (qui réalise la conversion d'un nombre entier en un nombre réel). Les constantes de ce langage sont zero : Int, true : Bool, false : Bool, unit : Unit. Pierce donne alors l'exemple de la catégorie où les objets sont Bool, Int, Real et Unit, et les flèches sont true, false, succInt, succReal, unit, iszero, not, toReal.
Les constantes sont des flèches, chacune d'entre elles associant l'unique élément de Unit à la valeur qu'elle représente.

Monomorphismes, épimorphismes et isomorphismes[modifier | modifier le code]
Définitions[modifier | modifier le code]
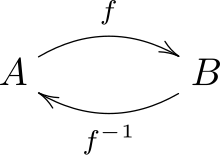
Une flèche est dite un monomorphisme lorsqu'elle vérifie la propriété suivante : pour tout couple de flèches (et donc aussi pour tout ), si , alors .
Une flèche est dite un épimorphisme lorsqu'elle vérifie la propriété suivante : pour tout couple de flèches (et donc aussi pour tout ), si , alors .
Les notions de monomorphisme et d'épimorphisme sont duales l'une de l'autre : une flèche est un monomorphisme si et seulement si elle est un épimorphisme dans la catégorie duale.
Une flèche est dite un isomorphisme s'il existe une flèche telle que et . Cette notion est autoduale.
Exemples et contre-exemples[modifier | modifier le code]
- Dans la catégorie des ensembles, les monomorphismes sont les injections, les épimorphismes sont les surjections et les isomorphismes sont les bijections.
- Un contre-exemple important en théorie des catégories : un morphisme peut à la fois être un monomorphisme et un épimorphisme, sans être pour autant un isomorphisme ; pour voir ce contre-exemple, il suffit de se placer dans la catégorie des anneaux commutatifs unitaires, et considérer la flèche (unique) : elle est un monomorphisme car provient d'une application injective, un épimorphisme par localisation, mais n'est clairement pas un isomorphisme.
- On trouve aussi de tels épimorphisme-monomorphisme non isomorphiques dans la catégorie des espaces topologiques : toute injection y est un monomorphisme, toute surjection est un épimorphisme, les isomorphismes sont les homéomorphismes, mais il y a des fonctions continues à la fois injectives et surjectives qui ne sont pas des homéomorphismes : par exemple l'identité sur un ensemble muni de deux topologies différentes, l'une plus grossière que l'autre.
- Les isomorphismes dans la catégorie des ensembles ordonnés sont les bijections croissantes dont la bijection réciproque est croissante (cette condition sur la bijection réciproque est automatiquement vérifiée dans le cas des ensembles totalement ordonnés, mais pas dans le cas général).
Somme et produit d'une famille d'objets en théorie des catégories[modifier | modifier le code]
La somme d'une famille est la donnée d'un objet de et pour tout d'une flèche vérifiant la propriété universelle :
- quels que soient l'objet et les flèches de il existe une unique flèche telle que pour tout le diagramme :

soit commutatif, c'est-à-dire que .
Le produit d'une famille est la donnée d'un objet de et pour tout d'une flèche vérifiant la propriété universelle :
- quels que soient l'objet et les flèches de il existe une unique flèche telle que pour tout le diagramme :

soit commutatif, c'est-à-dire que .
S'ils existent, les sommes et les produits sont uniques aux isomorphismes près[10].
On permute ces définitions en inversant les flèches des diagrammes : une somme (respectivement un produit) dans est un produit (respectivement une somme) dans sa duale.
Une catégorie cartésienne est une catégorie munie d'un objet final et du produit binaire. Une catégorie cartésienne fermée est une catégorie cartésienne munie de l'exponentiation.
En tant que fondement des mathématiques[modifier | modifier le code]
William Lawvere est le premier à avoir considéré la théorie des catégories comme potentiel fondement des mathématiques. En 1964, il propose une axiomatisation de la théorie des ensembles dans le langage des catégories[11],[12]. En 1966, il publie une théorie de la catégorie des catégories dans laquelle tous les objets mathématiques peuvent être exprimés et leurs propriétés démontrées[13]. La première version de cette catégorie des catégories avait été développée dans sa thèse de doctorat de 1963[14].
La théorie des catégories a donc été proposée comme fondement des mathématiques en au moins deux sens distincts[15]. En un premier sens, elle fournirait une axiomatisation alternative au concept d’ensembles. En comparaison avec l'axiomatisation de ZF, cette formulation ne place pas au premier plan la notion d’être « élément de » (x ∊ X). C’est plutôt la notion de fonction, exprimée par les morphismes de la catégorie, qui est fondamentale. La catégorie des ensembles s’est avérée être un exemple particulier de topos élémentaire, un type de catégorie inspiré des topos de Grothendieck[16].
Le second type de proposition consiste plutôt à dire que tous les concepts mathématiques importants peuvent être exprimés dans le langage des catégories. Alors que le premier type de fondement est logique et propose un système axiomatique, ce second type de fondement est plutôt méthodologique et offre une manière de comparer entre eux différents domaines des mathématiques à l’aide d’un langage commun. Ces deux propositions ne sont pas nécessairement incompatibles, la question des fondements de mathématiques pouvant prendre plusieurs sens[17],[18].
Cependant, toutes ces propositions concernant les fondements qui font appel aux catégories ont un point en commun. Elles s’inscrivent dans une perspective structuraliste des mathématiques. On entend par cette expression que les propriétés importantes des objets mathématiques sont les relations qui existent entre eux et non pas des propriétés intrinsèques aux objets eux-mêmes. Pour les structuralistes, un objet mathématique se définit donc entièrement par la place qu’il occupe dans une structure mathématique. Par exemple, le fait que le nombre 3 s’écrit avec le symbole “3” n’est pas une propriété structurelle, mais le fait d’être entre 2 et 4 dans l’ordre des nombres naturels est une telle propriété[19],[20]. La théorie des catégories est particulièrement adéquate afin d’exprimer une telle fondation, puisque les objets d’une catégorie ne sont définis qu’à isomorphisme près. Cela signifie que deux objets isomorphes et qui possèdent donc la même structure ne peuvent être distingués l’un de l’autre au sein d'une catégorie. Le langage des catégories exprime donc uniquement les propriétés structurelles de ces objets[21].
Tous les structuralistes ne sont cependant pas partisans de la théorie des catégories comme fondement[22],[23].
Notes et références[modifier | modifier le code]
- (en) Saunders Mac Lane, Categories for the Working Mathematician [détail de l’édition]
- Henri Cartan, dans le film Une vie de mathématicien qui lui est consacré, confie que Bourbaki aurait probablement commencé ses Éléments par les catégories si elles étaient apparues plus tôt.
- Richard Ewen Borcherds consacre une video "Categories pour le mathématicien oisif" à exposer ces axiomes
- Georges Poitou et Paul Jaffard, Introduction aux catégories et aux problèmes universels, Paris, Ediscience, , p. 4.
- (en) D.E Rydehear, Burstall, Computational category theory, Prentice hall, , Chapter 3, Section 3.1, Definition 2
- Cf. par exemple (en) Roy L. Crole, Categories for Types, CUP, , 335 p. (ISBN 978-0-521-45701-9, lire en ligne), p. 61. Signalons que Mac Lane appelle « métacatégorie » ce qui est appelé ici « catégorie », qu'il nomme « catégorie » ce qu'on appelle couramment « petite catégorie », et qu'il réserve le nom de « petite catégorie » à une notion encore plus restrictive.
- (en) Jan R. Strooker, Introduction to Categories, Homological Algebra and Sheaf Cohomology, Cambridge, Cambridge University Press, (ISBN 978-0-521-21699-9, OCLC 3168073), p. 4.
- (en) Benjamin C. Pierce, Basic category theory for computer scientist : Fondations of computation series, The MIT Press, , p. 5
- Poitou et Jaffard 1971, p. 7.
- Michel Zisman, Topologie algébrique élémentaire, Armand Colin, 1972, p. 10.
- (en) William Lawvere, « An elementary theory of the category of sets », Proceedings of the National Academy of Sciences of the U.S.A, , p. 1506–1511 (lire en ligne)
- (en) Tom Leinster, « Rethinking Set Theory », The American Mathematical Monthly, , p. 403-415 (lire en ligne)
- (en) William Lawvere, Proceedings of the Conference on Categorical Algebra, , « The category of categories as a foundation for mathematics », p. 1-20
- (en) William Lawvere, « Functorial Semantics of Algebraic Theories », Reprints in Theory and Applications of Categories, , p. 1-121 (lire en ligne)
- (en) J. L. Bell, « Category Theory and the Foundations of Mathematics », The British Journal for the Philosophy of Science, Vol. 32, No. 4, , p. 349-358 (lire en ligne)
- (en) Colin McLarty, « Exploring categorical structuralism », Philosophia Mathematica (3) 12, , p. 37-53
- (en) Jean-Pierre Marquis, « Category Theory and the Foundations of Mathematics: Philosophical Excavations », Synthese (103), , p. 421-447
- (en) Stewart Shapiro, « Foundations of Mathematics: Metaphysics, Epistemology, Structure », The Philosophical Quarterly (1950-), Vol. 54, No. 214, , p. 16-37 (lire en ligne)
- (en) Colin McLarty, « Numbers Can Be Just What They Have To », Noûs, Vol. 27, No. 4, , p. 487-498 (lire en ligne)
- (en) Julian Cole, « Mathematical Structuralism Today », Philosophy Compass 5/8, , p. 689–699
- (en) Steve Awodey, « Structure in mathematics and logic: A categorical perspective », Philosophia Mathematica (3) 4, , p. 209-237
- (en) Michael Resnick, Mathematics As a Science of Patterns, Oxford University Press,
- (en) Stewart Shapiro, Philosophy of Mathematics : Structure and Ontology, Oxford University Press,
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
Ouvrages de base :
- (en) Saunders Mac Lane, Categories for the Working Mathematician [détail de l’édition]
- (en) Emily Riehl, Category Theory in Context [détail de l’édition] (lire en ligne)
- Régine et Adrien Douady, Algèbre et théories galoisiennes [détail des éditions]
En français :
- Boileau, A. & Joyal, A., 1981, “La logique des topos”, Journal of Symbolic Logic, 46 (1): 6–16.
- Dieudonné, J. & Grothendieck, A., 1960 [1971], Éléments de Géométrie Algébrique, Berlin: Springer-Verlag.
- Grothendieck, A., 1957, “Sur quelques points d'algèbre homologique”, Tohoku Mathematics Journal, 9: 119–221.
- Grothendieck, A. et al., Séminaire de Géométrie Algébrique, Vol. 1–7, Berlin: Springer-Verlag.
En anglais :
- Adamek, J. et al., 1990, Abstract and Concrete Categories: The Joy of Cats, New York: Wiley.
- Adamek, J. et al., 1994, Locally Presentable and Accessible Categories, Cambridge: Cambridge University Press.
- Arzi-Gonczaworski, Z., 1999, “Perceive This as That — Analogies, Artificial Perception, and Category Theory”, Annals of Mathematics and Artificial Intelligence, 26 (1): 215–252.
- Awodey, S., 1996, “Structure in Mathematics and Logic: A Categorical Perspective”, Philosophia Mathematica, 3: 209–237.
- Awodey, S., 2004, “An Answer to Hellman's Question: Does Category Theory Provide a Framework for Mathematical Structuralism”, Philosophia Mathematica, 12: 54–64.
- Awodey, S., 2006, Category Theory, Oxford: Clarendon Press.
- Awodey, S., 2007, “Relating First-Order Set Theories and Elementary Toposes”, The Bulletin of Symbolic, 13 (3): 340–358.
- Awodey, S., 2008, “A Brief Introduction to Algebraic Set Theory”, The Bulletin of Symbolic, 14 (3): 281–298.
- Awodey, S. & Butz, C., 2000, “Topological Completeness for Higher Order Logic”, Journal of Symbolic Logic, 65 (3): 1168–1182.
- Awodey, S. & Reck, E. R., 2002, “Completeness and Categoricity I. Nineteen-Century Axiomatics to Twentieth-Century Metalogic”, History and Philosophy of Logic, 23 (1): 1–30.
- Awodey, S. & Reck, E. R., 2002, “Completeness and Categoricity II. Twentieth-Century Metalogic to Twenty-first-Century Semantics”, History and Philosophy of Logic, 23 (2): 77–94.
- Awodey, S. & Warren, M., 2009, “Homotopy theoretic Models of Identity Types”, Mathematical Proceedings of the Cambridge Philosophical Society, 146 (1): 45–55.
- Baez, J., 1997, “An Introduction to n-Categories”, Category Theory and Computer Science, Lecture Notes in Computer Science (Volume 1290), Berlin: Springer-Verlag, 1–33.
- Baez, J. & Dolan, J., 1998a, “Higher-Dimensional Algebra III. n-Categories and the Algebra of Opetopes”, Advances in Mathematics, 135: 145–206.
- Baez, J. & Dolan, J., 1998b, “Categorification”, Higher Category Theory (Contemporary Mathematics, Volume 230), Ezra Getzler (de) et Mikhail Kapranov (eds.), Providence: AMS, 1–36.
- Baez, J. & Dolan, J., 2001, “From Finite Sets to Feynman Diagrams”, Mathematics Unlimited – 2001 and Beyond, Berlin: Springer, 29–50.
- Baianu, I. C., 1987, “Computer Models and Automata Theory in Biology and Medecine”, in Witten, Matthew, Eds. Mathematical Modelling, Vol. 7, 1986, chapter 11, Pergamon Press, Ltd., 1513–1577.
- Barr, M. & Wells, C., 1985, Toposes, Triples and Theories, New York: Springer-Verlag.
- Barr, M. & Wells, C., 1999, Category Theory for Computing Science, Montreal: CRM.
- Batanin, M., 1998, “Monoidal Globular Categories as a Natural Environment for the Theory of Weak n-Categories”, Advances in Mathematics, 136: 39–103.
- Bell, J. L., 1981, “Category Theory and the Foundations of Mathematics”, British Journal for the Philosophy of Science, 32: 349–358.
- Bell, J. L., 1982, “Categories, Toposes and Sets”, Synthese, 51 (3): 293–337.
- Bell, J. L., 1986, “From Absolute to Local Mathematics”, Synthese, 69 (3): 409–426.
- Bell, J. L., 1988, “Infinitesimals”, Synthese, 75 (3): 285–315.
- Bell, J. L., 1988, Toposes and Local Set Theories: An Introduction, Oxford: Oxford University Press.
- Bell, J. L., 1995, “Infinitesimals and the Continuum”, Mathematical Intelligencer, 17 (2): 55–57.
- Bell, J. L., 1998, A Primer of Infinitesimal Analysis, Cambridge: Cambridge University Press.
- Bell, J. L., 2001, “The Continuum in Smooth Infinitesimal Analysis”, Reuniting the Antipodes — Constructive and Nonstandard Views on the Continuum (Synthese Library, Volume 306), Dordrecht: Kluwer, 19–24.
- Birkoff, G. & Mac Lane, S., 1999, Algebra, 3rd ed., Providence: AMS.
- Blass, A., 1984, “The Interaction Between Category Theory and Set Theory”, in Mathematical Applications of Category Theory (Volume 30), Providence: AMS, 5–29.
- Blass, A. & Scedrov, A., 1983, “Classifying Topoi and Finite Forcing”, Journal of Pure and Applied Algebra, 28: 111–140.
- Blass, A. & Scedrov, A., 1989, Freyd's Model for the Independence of the Axiom of Choice, Providence: AMS.
- Blass, A. & Scedrov, A., 1992, “Complete Topoi Representing Models of Set Theory”, Annals of Pure and Applied Logic , 57 (1): 1–26.
- Blute, R. & Scott, P., 2004, “Category Theory for Linear Logicians”, in Linear Logic in Computer Science, T. Ehrhard, P. Ruet, J-Y. Girard, P. Scott, eds., Cambridge: Cambridge University Press, 1–52.
- Borceux, F., 1994, Handbook of Categorical Algebra, 3 volumes, Cambridge: Cambridge University Press.
- Bunge, M., 1974, “Topos Theory and Souslin's Hypothesis”, Journal of Pure and Applied Algebra, 4: 159–187.
- Bunge, M., 1984, “Toposes in Logic and Logic in Toposes”, Topoi, 3 (1): 13–22.
- Carter, J., 2008, “Categories for the working mathematician: making the impossible possible”, Synthese, 162 (1): 1–13.
- Cheng, E. & Lauda, A., 2004, Higher-Dimensional Categories: an illustrated guide book, available at: http://cheng.staff.shef.ac.uk/guidebook/index.html
- Cockett, J. R. B. & Seely, R. A. G., 2001, “Finite Sum-product Logic”, Theory and Applications of Categories (electronic), 8: 63–99.
- Couture, J. & Lambek, J., 1991, “Philosophical Reflections on the Foundations of Mathematics”, Erkenntnis, 34 (2): 187–209.
- Couture, J. & Lambek, J., 1992, “Erratum:”Philosophical Reflections on the Foundations of Mathematics“”, Erkenntnis, 36 (1): 134.
- Crole, R. L., 1994, Categories for Types, Cambridge: Cambridge University Press.
- Ehresmann, A. & Vanbremeersch, J.-P., 2007, Memory Evolutive Systems: Hierarchy, Emergence, Cognition, Amsterdam: Elsevier
- Ehresmann, A. C. & Vanbremeersch, J-P., 1987, “Hierarchical Evolutive Systems: a Mathematical Model for Complex Systems”, * Bulletin of Mathematical Biology, 49 (1): 13–50.
- Eilenberg, S. & Cartan, H., 1956, Homological Algebra, Princeton: Princeton University Press.
- Eilenberg, S. & Mac Lane, S., 1942, “Group Extensions and Homology”, Annals of Mathematics, 43: 757–831.
- Eilenberg, S. & Mac Lane, S., 1945, “General Theory of Natural Equivalences”, Transactions of the American Mathematical Society, 58: 231–294.
- Eilenberg, S. & Steenrod, N., 1952, Foundations of Algebraic Topology, Princeton: Princeton University Press.
- Ellerman, D., 1988, “Category Theory and Concrete Universals”, Erkenntnis, 28: 409–429.
- Feferman, S., 1977, “Categorical Foundations and Foundations of Category Theory”, Logic, Foundations of Mathematics and Computability, R. Butts (ed.), Reidel, 149–169.
- Feferman, S., 2004, “Typical Ambiguity: trying to have your cake and eat it too”, One Hundred Years of Russell's Paradox, G. Link (ed.), Berlin: De Gruyter, 135–151.
- Freyd, P., 1964, Abelian Categories. An Introduction to the Theory of Functors, New York: Harper & Row.
- Freyd, P., 1965, “The Theories of Functors and Models”. Theories of Models, Amsterdam: North Holland, 107–120.
- Freyd, P., 1972, “Aspects of Topoi”, Bulletin of the Australian Mathematical Society, 7: 1–76.
- Freyd, P., 1980, “The Axiom of Choice”, Journal of Pure and Applied Algebra, 19: 103–125.
- Freyd, P., 1987, “Choice and Well-Ordering”, Annals of Pure and Applied Logic, 35 (2): 149–166.
- Freyd, P., 1990, Categories, Allegories, Amsterdam: North Holland.
- Freyd, P., 2002, “Cartesian Logic”, Theoretical Computer Science, 278 (1–2): 3–21.
- Freyd, P., Friedman, H. & Scedrov, A., 1987, “Lindembaum Algebras of Intuitionistic Theories and Free Categories”, Annals of Pure and Applied Logic, 35 (2): 167–172.
- Galli, A. & Reyes, G. & Sagastume, M., 2000, “Completeness Theorems via the Double Dual Functor”, Studia Logical, 64 (1): 61–81.
- Ghilardi, S., 1989, “Presheaf Semantics and Independence Results for some Non-classical first-order logics”, Archive for Mathematical Logic, 29 (2): 125–136.
- Ghilardi, S. & Zawadowski, M., 2002, Sheaves, Games & Model Completions: A Categorical Approach to Nonclassical Propositional Logics, Dordrecht: Kluwer.
- Goldblatt, R., 1979, Topoi: The Categorical Analysis of Logic, Studies in logic and the foundations of mathematics, Amsterdam: Elsevier.
- Hatcher, W. S., 1982, The Logical Foundations of Mathematics, Oxford: Pergamon Press.
- Healy, M. J., 2000, “Category Theory Applied to Neural Modeling and Graphical Representations”, Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks: IJCNN200, Como, vol. 3, M. Gori, S-I. Amari, C. L. Giles, V. Piuri, eds., IEEE Computer Science Press, 35–40.
- Healy, M. J., & Caudell, T. P., 2006, “Ontologies and Worlds in Category Theory: Implications for Neural Systems”, Axiomathes, 16 (1–2): 165–214.
- Hellman, G., 2003, “Does Category Theory Provide a Framework for Mathematical Structuralism?”, Philosophia Mathematica, 11 (2): 129–157.
- Hellman, G., 2006, “Mathematical Pluralism: the case of smooth infinitesimal analysis”, Journal of Philosophical Logic, 35 (6): 621–651.
- Hermida, C. & Makkai, M. & Power, J., 2000, “On Weak Higher-dimensional Categories I”, Journal of Pure and Applied Algebra, 154 (1–3): 221–246.
- Hermida, C. & Makkai, M. & Power, J., 2001, “On Weak Higher-dimensional Categories 2”, Journal of Pure and Applied Algebra, 157 (2–3): 247–277.
- Hermida, C. & Makkai, M. & Power, J., 2002, “On Weak Higher-dimensional Categories 3”, Journal of Pure and Applied Algebra, 166 (1–2): 83–104.
- Hyland, J. M. E. & Robinson, E. P. & Rosolini, G., 1990, “The Discrete Objects in the Effective Topos”, Proceedings of the London Mathematical Society (3), 60 (1): 1–36.
- Hyland, J. M. E., 1982, “The Effective Topos”, Studies in Logic and the Foundations of Mathematics (Volume 110), Amsterdam: North Holland, 165–216.
- Hyland, J. M. E., 1988, “A Small Complete Category”, Annals of Pure and Applied Logic, 40 (2): 135–165.
- Hyland, J. M. E., 1991, “First Steps in Synthetic Domain Theory”, Category Theory (Como 1990) (Lecture Notes in Mathematics, Volume 1488), Berlin: Springer, 131–156.
- Hyland, J. M. E., 2002, “Proof Theory in the Abstract”, Annals of Pure and Applied Logic, 114 (1–3): 43–78.
- Jacobs, B., 1999, Categorical Logic and Type Theory, Amsterdam: North Holland.
- Johnstone, P. T., 1977, Topos Theory, New York: Academic Press.
- Johnstone, P. T., 1979a, “Conditions Related to De Morgan's Law”, Applications of Sheaves (Lecture Notes in Mathematics, Volume 753), Berlin: Springer, 479–491.
- Johnstone, P. T., 1979b, “Another Condition Equivalent to De Morgan's Law”, Communications in Algebra, 7 (12): 1309–1312.
- Johnstone, P. T., 1981, “Tychonoff's Theorem without the Axiom of Choice”, Fundamenta Mathematicae, 113 (1): 21–35.
- Johnstone, P. T., 1982, Stone Spaces, Cambridge:Cambridge University Press.
- Johnstone, P. T., 1985, “How General is a Generalized Space?”, Aspects of Topology, Cambridge: Cambridge University Press, 77–111.
- Johnstone, P. T., 2001, “Elements of the History of Locale Theory”, Handbook of the History of General Topology, Vol. 3, * Dordrecht: Kluwer, 835–851.
- Johnstone, P. T., 2002a, Sketches of an Elephant: a Topos Theory Compendium. Vol. 1 (Oxford Logic Guides, Volume 43), Oxford: Oxford University Press.
- Joyal, A. & Moerdijk, I., 1995, Algebraic Set Theory, Cambridge: Cambridge University Press.
- Kan, D. M., 1958, “Adjoint Functors”, Transactions of the American Mathematical Society, 87: 294–329.
- Kock, A., 2006, Synthetic Differential Geometry (London Mathematical Society Lecture Note Series, Volume 51), Cambridge: Cambridge University Press, 2e éd.
- Krömer, R., 2007, Tool and Objects: A History and Philosophy of Category Theory, Basel: Birkhäuser.
- La Palme Reyes, M., John Macnamara, Gonzalo E. Reyes, and Houman Zolfaghari, 1994, “The non-Boolean Logic of Natural Language Negation”, Philosophia Mathematica, 2 (1): 45–68.
- La Palme Reyes, M., John Macnamara, Gonzalo E. Reyes, and Houman Zolfaghari, 1999, “Count Nouns, Mass Nouns, and their Transformations: a Unified Category-theoretic Semantics”, Language, Logic and Concepts, Cambridge: MIT Press, 427–452.
- Lambek, J., 1968, “Deductive Systems and Categories I. Syntactic Calculus and Residuated Categories”, Mathematical Systems Theory, 2: 287–318.
- Lambek, J., 1969, “Deductive Systems and Categories II. Standard Constructions and Closed Categories”, Category Theory, Homology Theory and their Applications I, Berlin: Springer, 76–122.
- Lambek, J., 1972, “Deductive Systems and Categories III. Cartesian Closed Categories, Intuition≠istic Propositional Calculus, and Combinatory Logic”, Toposes, Algebraic Geometry and Logic (Lecture Notes in Mathematics, Volume 274), Berlin: Springer, 57–82.
- Lambek, J., 1982, “The Influence of Heraclitus on Modern Mathematics”, Scientific Philosophy Today, J. Agassi and R.S. Cohen, eds., Dordrecht, Reidel, 111–122.
- Lambek, J., 1986, “Cartesian Closed Categories and Typed lambda calculi”, Combinators and Functional Programming Languages (Lecture Notes in Computer Science, volume 242), Berlin: Springer, 136–175.
- Lambek, J., 1989a, “On Some Connections Between Logic and Category Theory”, Studia Logica, 48 (3): 269–278.
- Lambek, J., 1989b, “On the Sheaf of Possible Worlds”, Categorical Topology and its relation to Analysis, Algebra and Combinatorics, Teaneck: World Scientific Publishing, 36–53.
- Lambek, J., 1993, “Logic without Structural Rules”, Substructural Logics (Studies in Logic and Computation, Volume 2), Oxford: Oxford University Press, 179–206.
- Lambek, J., 1994a, “Some Aspects of Categorical Logic”, Logic, Methodology and Philosophy of Science IX (Studies in Logic and the Foundations of Mathematics, Volume 134), Amsterdam: North Holland, 69–89.
- Lambek, J., 1994b, “Are the Traditional Philosophies of Mathematics Really Incompatible?”, Mathematical Intelligencer, 16 (1): 56–62.
- Lambek, J., 1994c, “What is a Deductive System?”, What is a Logical System? (Studies in Logic and Computation, Volume 4), Oxford: Oxford University Press, 141–159.
- Lambek, J., 2004, “What is the world of Mathematics? Provinces of Logic Determined”, Annals of Pure and Applied Logic, 126: 1–3, 149–158.
- Lambek, J. & Scott, P.J., 1981, “Intuitionistic Type Theory and Foundations”, Journal of Philosophical Logic, 10 (1): 101–115.
- Lambek, J. & Scott, P.J., 1983, “New Proofs of Some Intuitionistic Principles”, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 29 (6): 493–504.
- Lambek, J. & Scott, P.J., 1986, Introduction to Higher Order Categorical Logic, Cambridge: Cambridge University Press.
- Landry, E., 1999, “Category Theory: the Language of Mathematics”, Philosophy of Science, 66 (3) (Supplement): S14–S27.
- Landry, E., 2001, “Logicism, Structuralism and Objectivity”, Topoi, 20 (1): 79–95.
- Landry, E., 2007, “Shared Structure need not be Shared Set-structure”, Synthese, 158 (1): 1–17.
- Landry, E. & Marquis, J.-P., 2005, “Categories in Context: Historical, Foundational and philosophical”, Philosophia Mathematica, 13: 1–43.
- Lawvere, F. W., 1963, “Functorial Semantics of Algebraic Theories”, Proceedings of the National Academy of Sciences U.S.A., 50: 869–872.
- Lawvere, F. W., 1964, “An Elementary Theory of the Category of Sets”, Proceedings of the National Academy of Sciences U.S.A., 52: 1506–1511.
- Lawvere, F. W., 1965, “Algebraic Theories, Algebraic Categories, and Algebraic Functors”, Theory of Models, Amsterdam: North Holland, 413–418.
- Lawvere, F. W., 1966, “The Category of Categories as a Foundation for Mathematics”, Proceedings of the Conference on Categorical Algebra, La Jolla, New York: Springer-Verlag, 1–21.
- Lawvere, F. W., 1969a, “Diagonal Arguments and Cartesian Closed Categories”, Category Theory, Homology Theory, and their Applications II, Berlin: Springer, 134–145.
- Lawvere, F. W., 1969b, “Adjointness in Foundations”, Dialectica, 23: 281–295.
- Lawvere, F. W., 1970, “Equality in Hyper doctrines and Comprehension Schema as an Adjoint Functor”, Applications of Categorical Algebra, Providence: AMS, 1–14.
- Lawvere, F. W., 1971, “Quantifiers and Sheaves”, Actes du Congrès International des Mathématiciens, Tome 1, Paris: Gauthier-Villars, 329–334.
- Lawvere, F. W., 1972, “Introduction”, Toposes, Algebraic Geometry and Logic, Lecture Notes in Mathematics, 274, Springer-Verlag, 1–12.
- Lawvere, F. W., 1975, “Continuously Variable Sets: Algebraic Geometry = Geometric Logic”, Proceedings of the Logic Colloquium Bristol 1973, Amsterdam: North Holland, 135–153.
- Lawvere, F. W., 1976, “Variable Quantities and Variable Structures in Topoi”, Algebra, Topology, and Category Theory, New York: Academic Press, 101–131.
- Lawvere, F. W., 1992, “Categories of Space and of Quantity”, The Space of Mathematics, Foundations of Communication and Cognition, Berlin: De Gruyter, 14–30.
- Lawvere, F. W., 1994a, “Cohesive Toposes and Cantor's lauter Ensein ”, Philosophia Mathematica, 2 (1): 5–15.
- Lawvere, F. W., 1994b, “Tools for the Advancement of Objective Logic: Closed Categories and Toposes”, The Logical Foundations of Cognition (Vancouver Studies in Cognitive Science, Volume 4), Oxford: Oxford University Press, 43–56.
- Lawvere, F. W., 2000, “Comments on the Development of Topos Theory”, Development of Mathematics 1950–2000, Basel: Birkhäuser, 715–734.
- Lawvere, F. W., 2002, “Categorical Algebra for Continuum Micro Physics”, Journal of Pure and Applied Algebra, 175 (1–3): 267–287.
- Lawvere, F. W., 2003, “Foundations and Applications: Axiomatization and Education. New Programs and Open Problems in the Foundation of Mathematics”, Bulletin of Symbolic Logic, 9 (2): 213–224.
- Lawvere, F. W. & Rosebrugh, R., 2003, Sets for Mathematics, Cambridge: Cambridge University Press.
- Lawvere, F. W. & Schanuel, S., 1997, Conceptual Mathematics: A First Introduction to Categories, Cambridge: Cambridge University Press.
- Leinster, T., 2002, “A Survey of Definitions of n-categories”, Theory and Applications of Categories, (electronic), 10: 1–70.
- Lurie, J., 2009, Higher Topos Theory, Princeton: Princeton University Press.
- Mac Lane, S., 1950, “Dualities for Groups”, Bulletin of the American Mathematical Society, 56: 485–516.
- Mac Lane, S., 1969, “Foundations for Categories and Sets”, Category Theory, Homology Theory and their Applications II, Berlin: Springer, 146–164.
- Mac Lane, S., 1969, “One Universe as a Foundation for Category Theory”, Reports of the Midwest Category Seminar III, Berlin: Springer, 192–200.
- Mac Lane, S., 1971, “Categorical algebra and Set-Theoretic Foundations”, Axiomatic Set Theory, Providence: AMS, 231–240.
- Mac Lane, S., 1975, “Sets, Topoi, and Internal Logic in Categories”, Studies in Logic and the Foundations of Mathematics (Volumes 80), Amsterdam: North Holland, 119–134.
- Mac Lane, S., 1981, “Mathematical Models: a Sketch for the Philosophy of Mathematics”, American Mathematical Monthly, 88 (7): 462–472.
- Mac Lane, S., 1986, Mathematics, Form and Function, New York: Springer.
- Mac Lane, S., 1988, “Concepts and Categories in Perspective”, A Century of Mathematics in America, Part I, Providence: AMS, 323–365.
- Mac Lane, S., 1989, “The Development of Mathematical Ideas by Collision: the Case of Categories and Topos Theory”, Categorical Topology and its Relation to Analysis, Algebra and Combinatorics, Teaneck: World Scientific, 1–9.
- Mac Lane, S., 1996, “Structure in Mathematics. Mathematical Structuralism”, Philosophia Mathematica, 4 (2): 174–183.
- Mac Lane, S., 1997, “Categorical Foundations of the Protean Character of Mathematics”, Philosophy of Mathematics Today, Dordrecht: Kluwer, 117–122.
- Mac Lane, S., 1998, Categories for the Working Mathematician, 2e édition, New York: Springer-Verlag.
- Mac Lane, S. & Moerdijk, I., 1992, Sheaves in Geometry and Logic, New York: Springer-Verlag.
- MacNamara, J. & Reyes, G., (eds.), 1994, The Logical Foundation of Cognition, Oxford: Oxford University Press.
- Makkai, M., 1987, “Stone Duality for First-Order Logic”, Advances in Mathematics, 65 (2): 97–170.
- Makkai, M., 1988, “Strong Conceptual Completeness for First Order Logic”, Annals of Pure and Applied Logic, 40: 167–215.
- Makkai, M., 1997a, “Generalized Sketches as a Framework for Completeness Theorems I”, Journal of Pure and Applied Algebra, 115 (1): 49–79.
- Makkai, M., 1997b, “Generalized Sketches as a Framework for Completeness Theorems II”, Journal of Pure and Applied Algebra, 115 (2): 179–212.
- Makkai, M., 1997c, “Generalized Sketches as a Framework for Completeness Theorems III”, Journal of Pure and Applied Algebra, 115 (3): 241–274.
- Makkai, M., 1998, “Towards a Categorical Foundation of Mathematics”, Lecture Notes in Logic (Volume 11), Berlin: Springer, 153–190.
- Makkai, M., 1999, “On Structuralism in Mathematics”, Language, Logic and Concepts, Cambridge: MIT Press, 43–66.
- Makkai, M. & Paré, R., 1989, Accessible Categories : the Foundations of Categorical Model Theory, Contemporary Mathematics 104, Providence: AMS.
- Makkai, M. & Reyes, G., 1977, First-Order Categorical Logic, Springer Lecture Notes in Mathematics 611, New York: Springer.
- Makkei, M. & Reyes, G., 1995, “Completeness Results for Intuitionistic and Modal Logic in a Categorical Setting”, Annals of Pure and Applied Logic, 72 (1): 25–101.
- Marquis, J.-P., 1993, “Russell's Logicism and Categorical Logicisms”, Russell and Analytic Philosophy, A. D. Irvine & G. A. Wedekind, (eds.), Toronto, University of Toronto Press, 293–324.
- Marquis, J.-P., 1995, “Category Theory and the Foundations of Mathematics: Philosophical Excavations”, Synthese, 103: 421–447.
- Marquis, J.-P., 2000, “Three Kinds of Universals in Mathematics?”, in Logical Consequence: Rival Approaches and New Studies in Exact Philosophy: Logic, Mathematics and Science, Vol. II, B. Brown & J. Woods (eds.), Oxford: Hermes, 191–212.
- Marquis, J.-P., 2006, “Categories, Sets and the Nature of Mathematical Entities”, in The Age of Alternative Logics. Assessing philosophy of logic and mathematics today, J. van Benthem, G. Heinzmann, Ph. Nabonnand, M. Rebuschi, H. Visser (eds.), Springer, 181–192.
- Marquis, J.-P., 2009, From a Geometrical Point of View: A Study in the History and Philosophy of Category Theory, Berlin: Springer.
- Marquis, J.-P. & Reyes, G., to appear, “The History of Categorical Logic: 1963–1977”, Handbook of the History of Logic, vol. 6, D. Gabbay & J. Woods, eds., Amsterdam: Elsevier.
- McLarty, C., 1986, “Left Exact Logic”, Journal of Pure and Applied Algebra, 41 (1): 63–66.
- McLarty, C., 1990, “Uses and Abuses of the History of Topos Theory”, British Journal for the Philosophy of Science, 41: 351–375.
- McLarty, C., 1991, “Axiomatizing a Category of Categories”, Journal of Symbolic Logic, 56 (4): 1243–1260.
- McLarty, C., 1992, Elementary Categories, Elementary Toposes, Oxford: Oxford University Press.
- McLarty, C., 1993, “Numbers Can be Just What They Have to”, Noûs, 27: 487–498.
- McLarty, C., 1994, “Category Theory in Real Time”, Philosophia Mathematica, 2 (1): 36–44.
- McLarty, C., 2004, “Exploring Categorical Structuralism”, Philosophia Mathematica, 12: 37–53.
- McLarty, C., 2005, “Learning from Questions on Categorical Foundations”, Philosophia Mathematica, 13 (1): 44–60.
- McLarty, C., 2006, “Emmy Noether's set-theoretic topology: from Dedekind to the rise of functors”, The Architecture of Modern * * Mathematics, J.J. Gray & J. Ferreiros, Oxford: Oxford University Press, 187–208.
- Moerdijk, I., 1984, “Heine-Borel does not imply the Fan Theorem”, Journal of Symbolic Logic, 49 (2): 514–519.
- Moerdijk, I., 1995a, “A Model for Intuitionistic Non-standard Arithmetic”, Annals of Pure and Applied Logic, 73 (1): 37–51.
- Moerdijk, I., 1998, “Sets, Topoi and Intuitionism”, Philosophia Mathematica, 6 (2): 169–177.
- Moerdijk, I. & Palmgren, E., 1997, “Minimal Models of Heyting Arithmetic”, Journal of Symbolic Logic, 62 (4): 1448–1460.
- Moerdijk, I. & Palmgren, E., 2002, “Type Theories, Toposes and Constructive Set Theory: Predicative Aspects of AST”, Annals of Pure and Applied Logic, 114 (1–3): 155–201.
- Moerdijk, I. & Reyes, G., 1991, Models for Smooth Infinitesimal Analysis, New York: Springer-Verlag.
- Pareigis, B., 1970, Categories and Functors, New York: Academic Press.
- Pedicchio, M. C. & Tholen, W., 2004, Categorical Foundations, Cambridge: Cambridge University Press.
- Peirce, B., 1991, Basic Category Theory for Computer Scientists, Cambridge: MIT Press.
- Pitts, A. M. & Taylor, P., 1989, “A Note of Russell's Paradox in Locally Cartesian Closed Categories”, Studia Logica, 48 (3): 377–387.
- Pitts, A. M., 1987, “Interpolation and Conceptual Completeness for Pretoposes via Category Theory”, Mathematical Logic and Theoretical Computer Science (Lecture Notes in Pure and Applied Mathematics, Volume 106), New York: Dekker, 301–327.
- Pitts, A. M., 1989, “Conceptual Completeness for First-order Intuitionistic Logic: an Application of Categorical Logic”, Annals of Pure and Applied Logic, 41 (1): 33–81.
- Pitts, A. M., 1992, “On an Interpretation of Second-order Quantification in First-order Propositional Intuitionistic Logic”, Journal of Symbolic Logic, 57 (1): 33–52.
- Pitts, A. M., 2000, “Categorical Logic”, Handbook of Logic in Computer Science, Vol.5, Oxford: Oxford University Press, 39–128.
- Plotkin, B., 2000, “Algebra, Categories and Databases”, Handbook of Algebra, Vol. 2, Amsterdam: Elsevier, 79–148.
- Porter, T., 2004, “Interpreted Systems and Kripke Models for Multiagent Systems from a Categorical Perspective”, Theoretical Computer Science, 323 (1–3): 235–266.
- Reyes, G., 1991, “A Topos-theoretic Approach to Reference and Modality”, Notre Dame Journal of Formal Logic, 32 (3): 359–391.
- Reyes, G. & Zawadowski, M., 1993, “Formal Systems for Modal Operators on Locales”, Studia Logica, 52 (4): 595–613.
- Reyes, G. & Zolfaghari, H., 1991, “Topos-theoretic Approaches to Modality”, Category Theory (Como 1990) (Lecture Notes in Mathematics, Volume 1488), Berlin: Springer, 359–378.
- Reyes, G. & Zolfaghari, H., 1996, “Bi-Heyting Algebras, Toposes and Modalities”, Journal of Philosophical Logic, 25 (1): 25–43.
- Reyes, G., 1974, “From Sheaves to Logic”, in Studies in Algebraic Logic, A. Daigneault, ed., Providence: AMS.
- Rodabaugh, S. E. & Klement, E. P., eds., Topological and Algebraic Structures in Fuzzy Sets: A Handbook of Recent Developments in the Mathematics of Fuzzy Sets (Trends in Logic, Volume 20), Dordrecht: Kluwer.
- Scedrov, A., 1984, Forcing and Classifying Topoi, Providence: AMS.
- Scott, P.J., 2000, “Some Aspects of Categories in Computer Science”, Handbook of Algebra, vol. 2, Amsterdam: North Holland, 3–77.
- Seely, R. A. G., 1984, “Locally Cartesian Closed Categories and Type Theory”, Mathematical Proceedings of the Cambridge Mathematical Society, 95 (1): 33–48.
- Shapiro, S., 2005, “Categories, Structures and the Frege-Hilbert Controversy: the Status of Metamathematics”, Philosophia Mathematica, 13 (1): 61–77.
- Sica, G., ed., 2006, What is Category Theory?, Florence, Polimetrica.
- Taylor, P., 1996, “Intuitionistic sets and Ordinals”, Journal of Symbolic Logic, 61: 705–744.
- Taylor, P., 1999, Practical Foundations of Mathematics, Cambridge: Cambridge University Press.
- Tierney, M., 1972, “Sheaf Theory and the Continuum Hypothesis”, Toposes, Algebraic Geometry and Logic, F.W. Lawvere (ed.), Springer Lecture Notes in Mathematics 274, 13–42.
- Van Oosten, J., 2002, “Realizability: a Historical Essay”, Mathematical Structures in Computer Science, 12 (3): 239–263.
- Van Oosten, J., 2008, Realizability: an Introduction to its Categorical Side (Studies in Logic and the Foundations of Mathematics, Volume 152), Amsterdam: Elsevier.
- Van der Hoeven, G. & Moerdijk, I., 1984a, “Sheaf Models for Choice Sequences”, Annals of Pure and Applied Logic, 27 (1): 63–107.
- Van der Hoeven, G. & Moerdijk, I., 1984b, “On Choice Sequences determined by Spreads”, Journal of Symbolic Logic, 49 (3): 908–916.
- Van der Hoeven, G. & Moerdijk, I., 1984c, “Constructing Choice Sequences for Lawless Sequences of Neighbourhood Functions”, Models and Sets (Lecture Notes in Mathematics, Volume 1103), Berlin: Springer, 207–234.
- Wood, R.J., 2004, “ Ordered Sets via Adjunctions”, Categorical Foundations, M. C. Pedicchio & W. Tholen, eds., Cambridge: Cambridge University Press.
- Yanofski, N., 2003, “A Universal Approach to Self-Referential Paradoxes, Incompleteness and Fixed Points”, The Bulletin of Symbolic Logic, 9 (3): 362–386.
Liens externes[modifier | modifier le code]
- (en) Théorie des catégories, sur le site de l'université McGill (Canada)
- (en) Jiří Adámek, Horst Herrlich et George E. Strecker, Abstract and Concrete Categories. The Joy of Cats























































