Diagramme commutatif

En mathématiques, et plus spécialement dans les applications de la théorie des catégories, un diagramme commutatif est un diagramme d'objets et de morphismes tels que, si l'on suit à travers le diagramme un chemin d'un objet à un autre, le résultat par composition des morphismes ne dépend que de l'objet de départ et de l'objet d'arrivée.
Exemple
[modifier | modifier le code]Le premier théorème d'isomorphisme est un triangle commutatif comme suit :
Puisque f = h ∘ φ, le diagramme de gauche est commutatif ; et puisque φ = k ∘ f, il en est de même pour le diagramme de droite.
Sur le diagramme de gauche, il est possible d'aller de G à im f par deux chemins différents : soit directement grâce à l'application f, soit par composition des applications h et φ. De même, le diagramme de droite est commutatif, puisqu'on peut aller de G à G/ ker f soit directement par l'application φ, soit par la composition de k par f en passant par l'objet intermédiaire im f.
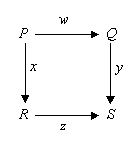
De la même manière, le carré ci-dessus est commutatif si y ∘ w = z ∘ x.
Vérification de la commutativité
[modifier | modifier le code]
La commutativité est aisément compréhensible pour un polygone avec un nombre fini de côtés (y compris seulement 1 ou 2), et un diagramme est commutatif si tout sous-diagramme polygonal est commutatif.
références
[modifier | modifier le code]Voir aussi
[modifier | modifier le code]