Spectrométrie de fluorescence des rayons X

La spectrométrie de fluorescence des rayons X (SFX ou FX, ou en anglais XRF pour X-ray fluorescence) est une technique d'analyse chimique utilisant une propriété physique de la matière, la fluorescence de rayons X.
Lorsque l'on bombarde de la matière avec des rayons X, la matière réémet de l'énergie sous la forme, entre autres, de rayons X ; c'est la fluorescence X, ou émission secondaire de rayons X.
Le spectre des rayons X émis par la matière est caractéristique de la composition de l'échantillon, en analysant ce spectre, on peut en déduire la composition élémentaire, c'est-à-dire les concentrations massiques en éléments.
L'analyse du spectre peut se faire de deux manières :
- par analyse dispersive en longueur d'onde (WD-XRF, wavelength dispersive X-ray fluorescence spectrometry) ;
- par analyse dispersive en énergie (ED-XRF, energy dispersive X-ray fluorescence spectrometry).
Historique[modifier | modifier le code]



- La spectrométrie de fluorescence X prend racines au début du XXe siècle, avec la découverte des rayons X par Wilhelm Röntgen en 1895[1]. Au cours du XIXe siècle, la spectroscopie dans le visible avait été assez développée pour que l'on sache dès 1850, que chaque élément chimique simple avait un spectre lumineux permettant de le reconnaître. Des instruments ont rapidement permis de déterminer la composition chimique de minéraux terrestres. En 1888, la formule de Rydberg affinait la précision théorique de l'émission caractéristique des éléments. La physique des rayons X a ensuite rapidement progressé, avec :
- Quelques années plus tard, Barkla nomme fluorescence X le rayonnement X secondaire, c'est-à-dire émis par un matériau lui-même soumis à un rayonnement X[2],[3],[4],[5]. Max von Laue a l'idée d'utiliser un cristal pour disperser les longueurs d'onde des rayons X, mais c'est à William Henry Bragg et à son fils William Lawrence que l'on doit l'essentiel de la théorie sur la diffraction des rayons X par un cristal et l'obtention en 1913 du premier spectre de rayons X. Ils publient en 1915 X-Rays and Crystal Structure[1].
- En 1913, la loi de Moseley, relie la fréquence ν de la raie et le numéro atomique Z d'un élément, concept développé par Niels Bohr[1].
Le spectromètre de Moseley est cependant limité par le faible rendement des tubes de l'époque[6]. - En 1922, Hadding, pour la première fois utilise la fluorescence X pour l'analyse de minéraux. Le spectre du rayonnement X représente une signature de l'élément chimique qui l'a émis beaucoup plus précise que les spectres obtenus dans le visible.
- Dès 1923, Coster et von Hevesy découvrent ainsi le hafnium, et en 1925 Walter Noddack et Ida Tacke découvrent le rhénium.
- En 1925, le spectromètre à dispersion de Bragg et la théorie de Moseley, donnent à la spectrométrie X une maturité suffisante pour que Karl Manne Georg Siegbahn publie un manuel complet de spectrométrie X[7].
- De 1925 à la fin de la Deuxième Guerre mondiale, de nombreux travaux d'analyse élémentaire, c'est-à-dire de détermination qualitative ou quantitative des éléments chimiques qui entrent dans la composition d'un matériau, sont menés dans les laboratoires, alors que s'améliorent les différents composants qui la rendent possible, notamment la source de rayons X et le cristal qui permet la diffraction. Le point faible reste la faible sensibilité du détecteur universellement utilisé à cette époque, à savoir l'émulsion photographique[2]. En fait, le spectromètre ne se réduit pas à un cristal et un détecteur : ces deux éléments essentiels doivent être inclus dans un goniomètre nécessairement mobile pour décrire une partie substantielle du spectre.
- En 1947, Norelco (North American Philips Company) commercialise[2] le 1er vrai spectromètre de fluorescence X, initialement construit par Friedman et Birks dans les laboratoires de recherche de la marine américaine à Washington, en utilisant le goniomètre d'un appareil destiné à contrôler l'orientation des cristaux de quartz.
- En 1954, un compteur Geiger équipe le premier diffractomètre commercialisé par Norelco et alors improprement appelé spectromètre. Le compteur Geiger, inventé en 1926, s'avère être la bonne alternative à l'émulsion photographique, en permettant le comptage unitaire des photons X[2].
- Dès 1951, Raimond Castaing teste un faisceau d'électrons pour provoquer une fluorescence X ; ce qui permet un spot électronique très petit, ouvrant la voie à des analyses locales à l'échelle du micromètre[2].
Mais, si la même fluorescence X est mise en jeu dans une sonde électronique que dans un appareil où la source d'excitation est un faisceau de rayons X, la méthode et théorie de quantification est complètement différente car les phénomènes de pénétration et d'absorption diffèrent pour les électrons et les rayons X. Les deux branches de la spectrométrie par fluorescence X seront amenées à diverger.
On réserve le nom de SFX (XRF) aux appareils utilisant une source de rayons X alors que lorsque la source primaire est un faisceau d'électrons, on parle plus volontiers de microanalyse (EPMA, en anglais, pour electron probe microanalysis). - En 1958, la société française Cameca commercialise une sonde électronique (dite microsonde de Castaing) associée à un ou plusieurs spectromètres X.
- Dans les années 1950, les compteurs Geiger sont remplacés par des compteurs proportionnels à gaz, d'abord scellés, puis à flux gazeux, qui permettent d'améliorer la précision de comptage[2]. Ceci améliore les deux techniques, SFX et microanalyse qui profitent aussi d'innovations dans la préparation des échantillons.
- En 1956, Fernand Claisse invente la technique de la perle fondue, consistant à dissoudre un minéral dans un verre pour l'analyser ; cela permet de réduire les problèmes liés aux effets de matrice[2]. La même année, J. Sherman propose des équations permettant de calculer de manière théorique les intensités en connaissant la composition de l'échantillon (équation corrigée par T. Shiraiwa et N. Fujino en 1966). Bien que la puissance de calcul ne permette pas d'inverser l'équation à l'époque — calculer les concentrations à partir des intensités — cela permet de proposer des approches empiriques de calculs[8].
- Fin des années 1960 ; L'analyse dispersive en énergie (EDS en anglais) est une alternative à l'analyse dispersive en longueur d'onde. Elle est permise par de nouveaux détecteurs à semi-conducteur capables de discriminer les rayons X selon leur énergie, c'est-à-dire de leur longueur d'onde[9]. Il s'agit de jonctions P+N dans la zone déserte de laquelle l'énergie du photon X génère des paires électrons-trous. Le nom donné à ces détecteurs au silicium dopés au lithium est Si(Li) ou silicon drift detector (détecteur à diffusion au silicium)[10]. Le Si(Li) devient le détecteur solide privilégié pour les analyses EDS[11]. En dépit d'une moindre résolution spectrale, ces détecteurs plus compacts permettent de produire des appareils moins chers, et en outre capables de mesurer simultanément tout le spectre sans déplacement mécanique. De simples microscopes électroniques à balayage peuvent recevoir en accessoire un analyseur EDS.

- L'informatique permet alors d'automatiser des séquences d'analyse, et de traiter les mesures en résolvant certains problèmes complexes posés par la soustraction du bruit de fond, la déconvolution des pics, le comptage en sortie des détecteurs et l'exploitation de modèles quantitatifs de plus en plus sophistiqués[2].
- Dès 1970, la sonde nucléaire (ou PIXE ; particle induced X-ray emission) utilise des particules (des ions) pour provoquer l'émission X[12]. Un faisceau d'ions peut être focalisé et contrairement au faisceau électronique, il est moins absorbé par l'air ; il n'est donc plus nécessaire de placer l'échantillon dans une chambre à vide, permettant des mesures in situ, non destructives (pour le non-vivant), à l'échelle micrométrique.
- En 1994, Niton (maintenant Thermo Fischer Scientific) commercialise le premier appareil portable[13]. De nombreux constructeurs proposent aujourd'hui des appareils pour un large spectre d'applications.
Physique de la fluorescence X[modifier | modifier le code]
Émission fluorescente[modifier | modifier le code]

Quand un matériau est soumis à un rayonnement de faible longueur d'onde et donc de forte énergie, comme les rayons X, les rayons gamma ou bien un faisceau d'électrons ou d'ions suffisamment accélérés, les atomes constituant le matériau peuvent subir une ionisation, c'est-à-dire qu'un ou plusieurs électrons peuvent être éjectés des couches électroniques (on parle aussi d'orbitales atomiques) de chacun de ces atomes. On appelle rayonnement primaire la source énergétique qui produit l'ionisation ; pour que celle-ci ait lieu, il est nécessaire que le rayonnement primaire soit assez énergétique pour arracher un électron de la couche interne de l'atome. Plus précisément, l'énergie des photons ou des particules primaires doit être plus grande que le potentiel d'ionisation. On appelle effet photoélectrique l'arrachement d'un électron sous l'effet d'un photon énergétique[14].
L'atome est alors dans un état excité mais la perte d'un électron a rendu la structure électronique de l'atome instable. La désexcitation se fait par une transition électronique : un électron d'un niveau plus élevé « descend » pour occuper la case quantique à moitié vide (place laissée vacante par le photoélectron, c'est-à-dire par l'électron éjecté par effet photoélectrique). Cette transition électronique libère l'énergie correspondant à la différence d'énergie des niveaux impliqués, soit par l'émission d'un photon X, soit en transmettant l'énergie à un des électrons atomiques. Le premier cas correspond à la fluorescence X, le second à l'émission Auger, les deux processus étant en compétition.
L'énergie du photon X émis est égale à la différence d'énergie des deux orbitales concernées. Il est donc caractéristique de l'atome où l'émission a été générée. On appelle spectre d'énergie la distribution des énergies de l'ensemble des photons émis. Le spectre d'énergie est donc caractéristique de la composition de l'échantillon. Le terme de fluorescence est appliqué aux phénomènes dans lesquels l'absorption d'un rayonnement produit la réémission d'un rayonnement moins énergétique[14].

Les électrons secondaires (Auger ou issus de l'interaction avec un rayon X ou une particule plus énergétique encore) peuvent à leur tour exciter les atomes, notamment les atomes légers comme le carbone ou l'azote[15], et provoquer de nouvelles émissions de fluorescence X ou Auger.
Chaque élément chimique est caractérisé par des orbitales électroniques d'une certaine énergie. Comme on peut le voir sur la figure Transitions électroniques, il n'y a qu'un petit nombre de transitions possibles. Les couches électroniques s'appelant K, L, M, N, la transition L→K est traditionnellement appelée Kα, la transition M→K est appelée Kβ, la transition M→L est appelée Lα et ainsi de suite (notation de Siegbahn). Chacune de ces transitions génère un photon fluorescent avec son énergie caractéristique et la longueur d'onde du photon est reliée à son énergie par la constante de Planck h[14]
Le rayonnement fluorescent peut donc être analysé de façon équivalente en énergie — on parle d'analyse dispersive en énergie — ou en longueur d'onde — on parle alors d'analyse dispersive en longueur d'onde. Le spectre du matériau analysé est l'intensité du rayonnement en fonction de l'énergie, généralement exprimée en électron-volts (eV) ou en longueur d'onde. C'est un outil puissant pour l'analyse chimique élémentaire, branche de la chimie analytique.
Bruit de fond[modifier | modifier le code]
Le bruit de fond du signal provient de toutes sortes de phénomènes dont certains sont inhérents à la fluorescence X et d'autres dépendent du type d'analyse par fluorescence X. Dans la pratique, il s'agit du fond continu que l'on peut voir sur les spectres présentés dans cet article. Le bruit de fond obère la limite de détection de l'analyse dans la mesure où les pics de trop faible intensité ne pourront pas être distingués de ce fond continu.
Le Bremsstrahlung se retrouve dans toute la famille d'analyse par fluorescence X. Ce bruit de fond est causé dans l'échantillon par les électrons éjectés par effet photoélectrique et par effet Compton. Un autre phénomène interne aux échantillons cristallisés ou partiellement cristallisés consiste en un phénomène de diffraction de rayons X qui va essentiellement perturber la mesure des raies d'éléments légers.
Lorsque la source primaire est un rayonnement X, et ce cas est désigné par « SFX » (XRF), dans le reste de l'article, un bruit de fond supplémentaire provient du fait que le rayonnement primaire est susceptible d'interférer avec le rayonnement secondaire :
- la diffusion Rayleigh du rayonnement du tube par l'échantillon : l'échantillon se comporte comme une sorte de miroir qui renvoie le signal du tube vers le détecteur, sans modification d'énergie ;
- l'effet Compton : le rayonnement du tube est diffusé par l'échantillon avec une perte d'énergie.
La diffusion Rayleigh est plus importante pour les échantillons « lourds » (c'est-à-dire comportant majoritairement des atomes de numéro atomique élevé), la diffusion Compton est plus importante pour des échantillons « légers » (c'est-à-dire comportant majoritairement des atomes de Z faible).
Lorsque la source primaire est un faisceau d'électrons, et ce cas est désigné par « microsonde » (EPMA) dans le reste de l'article, le Brehmstralung est dominé par une interaction électron-matière spécifique : Les électrons peuvent être soumis à un champ électrique décélérateur créé à l'échelle atomique entre le noyau chargé positivement et les couches électroniques. La perte d'énergie cinétique de l'électron résulte produit alors un photon dans une large gamme d'énergie[16].
Effets de matrice[modifier | modifier le code]
En fluorescence X, l'intensité d'une raie n'est pas toujours proportionnelle à la concentration de l'élément : les autres atomes constituant l'échantillon modifient le signal, c'est ce que l'on appelle les « effets de matrice ». Certains effets de matrices sont physiques, c'est-à-dire qu'ils ne mettent en jeu que la composition élémentaire de l'échantillon. Dans le cas de la SFX, ils mettent en jeu deux phénomènes : l'absorption et la fluorescence secondaire.
Le niveau de signal dépend en effet de l'absorption des rayons X par l'échantillon avant qu'ils n'atteignent l'atome cible. On parle d'absorption primaire. L'absorption secondaire joue sur le rayonnement résultant de la fluorescence X entre l'atome cible et la surface de l'échantillon. La fluorescence secondaire, ou surexcitation, désigne l'excitation d'un atome voisin par les rayons X secondaires. Les atomes de l'échantillon reçoivent donc des rayons X venant du tube et des rayons X venant d'autres atomes.
Dans le cas de l'EPMA, les mêmes phénomènes se produisent, mais c'est l'interaction des électrons avec la matrice, plus précisément la perte d'énergie des électrons lorsqu'ils pénètrent dans l'échantillon, qui joue le rôle de l'absorption primaire. La profondeur de pénétration des électrons dans le matériau dépend essentiellement du numéro atomique Z des composants de l'échantillon et de l'énergie cinétiques des électrons incidents. On désigne ainsi les effets de matrice par l'acronyme ZAF, où Z est le numéro atomique, A l'absorption et F la fluorescence[17].
L'absorption des rayons X par un matériau donné dépend à la fois de la longueur d'onde considérée et des constituants du matériau. Globalement, plus le numéro atomique de l'élément est élevé, plus grande sera l'absorption[18]. Pour fixer les ordres de grandeur, un photon de 183 eV, qui correspond à la raie Kα du Bore, a une profondeur de pénétration de 50 nm dans le silicium, alors qu'un photon de 8 048 eV, qui correspond à la raie Kα du cuivre, a une profondeur de pénétration de 4 μm dans le silicium, de 3 μm dans le fer et 240 nm dans l'or[19].
Les effets de matrices physiques peuvent être quantifiés assez convenablement, car les différents phénomènes physiques sont bien établis et bien documentés. Il existe aussi des effets de matrices chimiques qui sont produits par l'émission de photons de basse énergie générés par des transitions sur des couches électroniques périphériques dont les niveaux d'énergie dépendent des liaisons chimiques. Ces effets chimiques se traduisent par un certain élargissement des pics et par un léger déplacement de ceux-ci. On peut les considérer comme des effets parasites, mais un appareillage particulièrement sensible pourra aussi renseigner sur la composition chimique de l'échantillon au vu des déplacements observés sur le spectre[20].
Mesure et sources d'erreur[modifier | modifier le code]
Une mesure de fluorescence X permet d'afficher un spectre, c'est-à-dire le nombre de photons X secondaires (émis par l'échantillon) ayant une énergie E/longueur d'onde λ donnée. En fait, on mesure un « nombre de coups », c'est-à-dire en nombre d'impulsion générées par le détecteur ; le rapport entre le nombre de photons pénétrant dans le détecteur et le nombre de coups généré dépend le rendement du détecteur et de l'amplification. On exprime en général l'intensité I en nombre de coups par seconde (cps) ; c'est le « taux de comptage ». Le spectre est la courbe I(λ) ou I(E). L'analyse qualitative — connaître les éléments présents — consiste à détecter si un pic est présent. L'analyse quantitative — déterminer la concentration d'un ou plusieurs éléments — nécessite de connaître la hauteur ou la surface d'un pic du spectre.
On a typiquement quatre sources d'erreur :
- le caractère aléatoire de l'émission de photons X (émission primaire par le tube et émission secondaire par l'échantillon), qui est un phénomène quantique ;
- dispersion de la mesure, qui provoque un élargissement des pics du spectre ; on a alors un risque de confusion de pics voisins (superposition de pics, « interférence ») ;
- bruit de fond, qui peut masquer de petits pics et perturber la mesure de la hauteur ou de la surface d'un pic ;
- les écarts entre le modèle de calcul et l'échantillon réel, en particulier le fait que l'échantillon n'est pas toujours homogène, dans le cas d'une roche broyée par exemple (effet de taille de grains, effets dits « minéralogiques »).
Instrumentation[modifier | modifier le code]
Source de rayonnement primaire[modifier | modifier le code]
Un spectromètre de fluorescence X comporte une source de rayons X qui peut être un générateur de rayons X, type tube de Coolidge, un faisceau issu produit par un synchrotron ou encore une source radioactive.
Dans le cas d'échantillons fragiles, il est souvent préférable d'utiliser un rayonnement indirect : le tube à rayons X bombarde une cible, et c'est le spectre fluorescent de cette cible qui bombarde l'échantillon. L'échantillon est excité par un rayonnement quasi monochromatique. Ceci nécessite un appareil adapté, et modifie le traitement des résultats puisqu'il faut prendre en compte l'influence de la cible. Cette méthode permet également de simplifier grandement les calculs des effets de matrice, puisque l'on utilise un rayonnement quasi-monochromatique. On parle dans ce cas de « fluorescence X polarisée ».
Une microsonde comporte un canon à électrons qui crée un faisceau focalisé. Ce faisceau peut être dévié et ainsi pointer vers un endroit spécifique de l'échantillon, ou encore effectuer un balayage ce qui donne une cartographie élémentaire.
De l'énergie caractéristique de la source du rayonnement primaire, longueur d'onde des rayons X pour la SFX ou tension d'accélération des électrons pour la microsonde, va dépendre à la fois de la profondeur sur laquelle l'échantillon sera susceptible de donner une réponse et de la gamme du spectre sur laquelle cette réponse sera donnée. Le spectre mesuré sera limité aux énergies inférieures à l'énergie caractéristique de la source primaire.
Spectromètres WDS et EDS[modifier | modifier le code]
Il existe deux manières de déterminer le spectre : l'analyse dispersive en longueur d'onde ou en énergie.
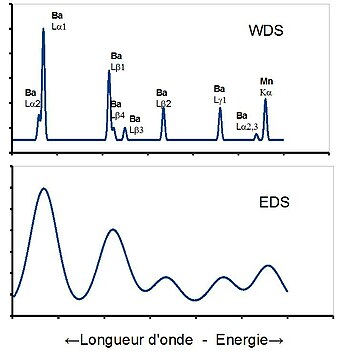
L'analyse dispersive en longueur d'onde est couramment appelée WDS, selon son acronyme anglais Wavelength dispersive spectrometry. On sélectionne les photons X d'une seule longueur d'onde par diffraction de Bragg sur un monocristal, en aval duquel on dispose un détecteur de photons qui peut être un compteur proportionnel à gaz ou un scintillateur. C'est l'angle entre la trajectoire du rayonnement secondaire et la surface du cristal qui détermine la longueur d'onde réfléchie. Le détecteur doit être disposé sur la trajectoire symétrique de la trajectoire secondaire.
Du principe de base, la sélection d'une seule longueur d'onde, découle un avantage et un inconvénient. L'avantage est de ne présenter sur le détecteur que le pic d'intérêt, ce qui est spécialement intéressant pour la mesure d'éléments trace dont le rayonnement X n'est alors pas parasité par le rayonnement caractéristique d'un élément de la matrice, qui peut être un million de fois plus intense que celui de l'élément trace.
La contrepartie est que pour mesurer tout un spectre, il est nécessaire de faire varier l'angle d'inclinaison du cristal tout en repositionnant le détecteur. Ceci implique donc la mise en mouvement d'un système mécanique de précision. De même, si on veut simplement mesurer plusieurs raies du spectres, il faudra régler séquentiellement le goniomètre — c'est le nom que l'on donne à ce système mécanique — aux différentes positions d'intérêt. On peut également doter l'appareil de plusieurs spectromètres WDS, chacun d'eux étant réglé aux positions d'intérêt pour l'analyse considérée[21] ; on parle d'appareil multicanal.

Un spectromètre à diffraction de Bragg peut avoir une excellente résolution spectrale sous réserve que la géométrie de la diffraction soit respectée[22] et qu'une restriction concernant l'émittance soit apportée : la surface émissive ou l'angle d'ouverture des trajectoires doivent être petits. Pour la SFX, la source n'est jamais très petite, on utilise un cristal plan et un collimateur, également appelé « fentes de Soller », qui est formé de fines lamelles de cuivre parallèles ; ainsi, on s'assure que tous les rayons secondaires qui frappent le cristal analyseur ont la même direction. Avec un cristal courbe (mesure à position fixe), on dispose une fente fine entre l'échantillon et le cristal analyseur, la fente, le cristal et le détecteur étant sur un cercle appelé « cercle de Rowland »[23]. Pour la microsonde où la sonde électronique est naturellement petite, on utilisera un cristal courbe[24].
Il n'est pas possible de couvrir toute la gamme du spectre des rayons X, c'est-à-dire moins de 500 eV pour les raies Kα des éléments les plus légers (Be, B, C, N) à plus de 60 keV pour la raie Kα1 des éléments plus lourds que le tungstène. Il est vrai qu'il n'est pas forcément nécessaire d'accéder à ces énergies pour mesurer des concentrations de tungstène, pour prendre cet exemple, puisque sa raie Lα1 est à 8,4 keV. D'après la relation de Bragg, la distance entre les plans atomiques du cristal doit être de l'ordre de grandeur de la longueur d'onde à détecter. Ainsi, pour les raies Kα des éléments lourds, on utilise des cristaux LiF (fluorure de lithium) dont la distance entre plans atomiques est de quelque 0,2 nanomètre, alors que pour les éléments légers, on utilisera une structure multicouches Mo/B4C qui n'est pas à proprement parler un cristal[25].
Dans le cas de l'analyse dispersive en énergie, les photons X de toutes les longueurs d'onde du spectre fluorescent parviennent jusqu'au détecteur. Le détecteur doit convertir chaque photon en une impulsion de charge électrique proportionnelle à l'énergie du photon.
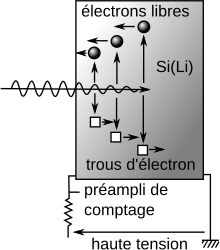
Les détecteurs à semi-conducteur, plus précisément du type SDD Si(Li) (silicon drift detector) sont de bons candidats pour cette fonction, puisque la génération de paires électron-trou dans la zone déserte d'une Jonction P-i-N est proportionnelle à l'énergie du photon[26]. Plus précisément, le nombre de charges électriques élémentaires générées est égal à /3,8, rapport de l'énergie du photon à 3,8 eV[27].
Là où le spectrométrie WDS met en jeu une mécanique et une technologie de formation du cristal sophistiquée, la spectrométrie EDS va mettre en jeu une électronique de détection sophistiquée pour discriminer les niveaux des impulsions de charge électronique. Le bruit thermique électronique est a priori un facteur limitant de la résolution spectrale, mais ce n'est pas la limitation physique fondamentale de la technique. On arrive en effet à le réduire à un assez faible niveau en refroidissant le détecteur[28].
La résolution spectrale de l'EDS est donc beaucoup moins bonne que celle de la spectrométrie WDS, comme le montre la figure où sont représentés deux spectres EDS et WDS du même échantillon. Il existe beaucoup d'applications qui ne requièrent pas une très haute résolution spectrale. La moins bonne résolution de l'EDS est compensée par la possibilité inhérente de mesurer tout le spectre simultanément.
| Performance instrumentale | WDS | EDS |
|---|---|---|
| Efficacité de collection géométrique | 0,2 à 0,5 % | 2 à 5 % |
| Rendement quantique | typ. 30 % | 100 % dans la gamme 2-16 keV |
| Résolution spectrale | 5 eV | 140 eV à 5,9 keV |
| Gamme spectrale de mesure instantanée | Résolution du spectromètre | Toute la gamme |
| Taux de comptage | typ. 50 000 cps | 3 000 cps |
| Artefacts | - | rejet d'empilement (**) réflexions parasites |
(*) avec un compteur proportionnel
(**) Voir ci-dessous, les détecteurs
Malgré un taux de comptage plus faible, les spectromètres EDS permettent de faire des mesures de spectres total plus rapides que les spectromètres WDS dans la mesure où, dans le cas WDS, l'intensité de la source primaire est généralement limitée pour que le compteur ne soit pas saturé sur les pics majeurs. Autrement dit, lors du balayage mécanique dont le pas est nécessairement équivalent à la très bonne résolution en énergie, typiquement 10 eV, le système de mesure ne compte pratiquement rien[29].
Les détecteurs[modifier | modifier le code]
Avec un spectromètre WDS, on utilise généralement un compteur proportionnel à gaz et un scintillateur. Pour faire du tri en énergie (spectromètre EDS), on utilise généralement un détecteur SDD. Mais on peut aussi utiliser un détecteur solide en combinaison avec un spectromètre WDS, et l'on peut aussi faire du tri en énergie avec un compteur proportionnel ou un scintillateur.
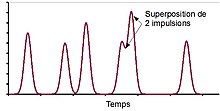
Quel que soit le type de compteur, un des problèmes à gérer est celui de deux impulsions trop rapprochées et que l'on ne peut pas distinguer l'une de l'autre. L'incidence d'un tel événement n'est pas le même dans le cas d'un spectromètre WDS ou dans le cas d'un spectromètre EDS. En effet, dans le cas d'un spectromètre WDS où toutes les impulsions sont supposées avoir été générées par des photons X de la même énergie, la superposition ne se traduit que la perte d'une impulsion, et ce cas est statistiquement prévisible : plus le taux de comptage est élevé, plus la probabilité qu'une impulsion soit très proche d'une autre impulsion (phénomène de saturation). On applique donc une correction de « temps mort » d'autant plus élevée que le taux de comptage est important[30].
Dans le cas d'une détection qui trie les impulsions en fonction de leur amplitude, la superposition de deux impulsions crée un artefact de mesure : la grosse impulsion sera interprétée comme provenant d'un photon X dont l'énergie est la somme des énergies de chacun des 2 photons X ayant généré les impulsions. Ce problème d'empilement est partiellement résolu en mettant en place une chaine de mesures rapide qui détecte l'évènement sans discriminer l'énergie. Il est alors possible de rejeter les impulsions produites par plusieurs évènements. Bien entendu, cette réjection n'est pas possible lorsque les deux évènements sont trop rapprochés pour pouvoir être distingués par cette chaine de mesure rapide[30].
Un compteur proportionnel à gaz est constitué par une enceinte cylindrique qui joue le rôle d'une cathode contenant un gaz, généralement mélange argon/méthane, un fil métallique coaxial, qui joue le rôle d'anode, porté à une tension positive par rapport à la cathode, une fenêtre d'entrée transparente aux rayons X mais étanche. Le compteur peut être scellé, mais il aura une durée de vie limitée car le gaz se contamine, ou bien il peut être conçu pour recevoir en permanence un flux gazeux, et sa durée de vie sera pratiquement illimitée. Lorsqu'un photon X d'énergie E0 pénètre dans le compteur, toute son énergie est absorbée pour ioniser un atome de gaz, initiant ainsi un processus qui aboutit à la formation d'un certain nombre n de paires ion-électrons[31] :
où ε vaut approximativement 30 eV[31]. Le courant électrique généré par ces ionisations est détecté et amplifié, et constitue l'impulsion. La hauteur de l'impulsion — l'intensité du courant — est proportionnelle à l'énergie du photon, mais avec une dispersion plus grande que celle obtenue avec les détecteurs EDS, mais plus petite que les différences d'énergie entre les photons de la raie mesurée et celle de photons parasites. La discrimination en énergie des compteurs proportionnels permet ainsi d'éliminer des impulsions parasites, provenant soit du fond continu pour les énergies plus basses, soit des réflexions de Bragg d'ordre supérieur à un pour les énergies plus hautes[30]. La discrimination en énergie n'est cependant pas suffisante pour avoir directement un spectre en énergie, d'où l'utilisation d'un cristal diffractant. Ce détecteur a un bon rendement pour les faibles énergies[30].
Les spectromètres EDS mettent en œuvre des détecteurs semi-conducteurs de type Si(Li) ou SDD (silicon drift detector). Un dispositif électronique discriminateur permet de compter les impulsions et de les trier par leurs amplitudes. La précision de détermination de l'amplitude des impulsions électriques et donc de l'énergie des photons X est d'autant meilleure que la température du détecteur est basse. On doit donc le refroidir par azote liquide ou par effet Peltier[32]. Le détecteur Si(Li), le plus répandu des détecteurs semiconducteurs en SFX, est une diode P-i-N, polarisée en inverse par une tension de 1 000 volts environ, dans laquelle le dopant P est du Bore et le dopant N du Lithium. La région P est située à la périphérie du dispositif, laissant une région intrinsèque d'environ 3 mm directement exposée aux rayons X. Cette région intrinsèque génère un bruit de fond particulièrement faible du fait que les « accepteurs » Bore y sont compensés par des « donneurs » Lithium[32]. Les détecteurs HPGe (High Purity Germanium) représentent une variante des détecteurs Si(Li), présentant une meilleure résolution spectrale pour les hautes énergies, mais limitée pour les basses énergies[33].
Le processus de détection d'une jonction P-i-N est très analogue à celui du compteur proportionnel : un photon X est converti en charges électriques, mais dans le cas de la jonction, la création de paires électron-trou joue le rôle de l'ionisation dans un compteur proportionnel. ε vaut approximativement 3,8 eV< La limitation fondamentale du détecteur Si(Li) est statistique : le nombre de charges électriques élémentaires n'est égal qu'en moyenne au rapport de l'énergie du photon à 3,8 eV, mais la dispersion obéit à une statistique poissonienne (bruit de grenaille) corrigée par un coefficient de Fano de 0,1 qui implique que l'incertitude de mesure sera supérieure à 100 eV lorsque l'énergie du photon est de 6,4 keV (raie de Fe Kα)[28].
L'électronique d'un système de mesure de l'énergie inclut la conversion de l'impulsion de charges électriques en impulsion de tension autour d'un préamplificateur faible bruit, un convertisseur analogique-numérique et un système de comptage multicanaux (MCA, comme Multichannel Analysis) gérant le spectre entier[34].
Un problème général des détecteurs est l'absorption de la couche de protection qui doit nécessairement exister en amont de la partie active du détecteur. Pour les compteurs à gaz, il s'agit de la « fenêtre » qui sépare l'enceinte du détecteur qui contient le gaz sous une faible pression de l'extérieur de l'enceinte qui est à la pression atmosphérique dans le cas de la SFX et sous vide dans le cas de la microsonde. Cette fenêtre est un film mince de béryllium ou d'un matériau organique comme la nitrocellulose ou le polypropylène. Avec ces matériaux, on obtient une bonne transparence, mais ces films minces sont un élément fragile de l'instrumentation[35],[36]. La zone active des détecteurs semi-conducteurs doit également être protégée, par exemple, par une couche mince d'or[37] qui, même lorsqu'elle est réduite à quelques nanomètres, reste opaque aux rayons X les plus mous. Dans la pratique, les détecteurs Si(Li) sont insensibles aux éléments légers, Be, B, C, N, dont la raie Kα correspond à une énergie inférieure à 500 eV[38]. Les détecteurs HPGe sont quant à eux pratiquement inutilisables pour des énergies inférieures à 3 keV[33].
Pour les photons X de grande énergie, le scintillateur est une alternative au compteur proportionnel. Il se compose d'un cristal fluorescent, par exemple en iodure de sodium NaI. Lorsqu'un photon X frappe le cristal, cela provoque un spot de lumière visible qui est détecté et amplifié par un photomultiplicateur. L'intensité lumineuse est proportionnelle à l'énergie du photon X incident, mais, pour le compteur proportionnel à gaz, avec une grande dispersion. Ce détecteur est bien adapté aux énergies élevées[39].
À côté des détecteurs Si(Li) et HPGe, des détecteurs en silicium de plus petite taille, que l'on désigne par « diode P-i-N » (ce qui, à proprement parler, ne les distingue pas des deux autres), peuvent être refroidis par simple effet Peltier et peuvent même être utilisés à température ambiante, se montrant particulièrement bien adaptés à l'intégration dans des appareils portables[33].
Pratique de l'analyse par fluorescence X[modifier | modifier le code]
Si la physique de base de la spectrométrie par fluorescence X est commune à toutes les branches de la famille, les problèmes pratiques d'analyse sont spécifiques à chaque branche. Ainsi, la préparation d'échantillons provenant de matériaux liquides n'a pas de sens en microanalyse EPMA qui est par définition une analyse locale. Seule la pratique de l'analyse SFX est traitée dans cet article alors que celle de la microsonde est traitée dans l'article Microsonde de Castaing.
Préparation des échantillons[modifier | modifier le code]
Selon la nature du matériau, l'échantillon mesuré peut être le matériau brut, sans préparation. C'est le cas d'un échantillon solide ayant une tenue mécanique suffisante et les bonnes dimensions, par exemple métal, verre ou polymère découpé aux bonnes dimensions.
Dans d'autres cas, l'échantillon doit faire l'objet d'une préparation[40] :
Dans le cas de la poudre, une fois le matériau broyé, il peut être mis dans une coupe dont le fond est un film polymère, l'analyse se faisant sous hélium pour éviter que la poudre ne vole sous l'effet du pompage[41]. Lorsque l'on dispose de peu de poudre, cette dernière peut également être pressée sur une pastille d'acide borique qui assure sa tenue mécanique[41]. Elle peut également être pressée sous la forme d'une pastille, avec ou sans liant. Les principaux liants utilisés sont la cire et la cellulose microcristalline. Certains utilisent des cachets d'aspirine non pelliculés achetés en pharmacie ; c'est en effet de la cellulose qui est généralement utilisée pour lier les cachets, et l'acide acétylsalicylique sert de lubrifiant. Il faut toutefois s'assurer que le cachet ne contienne pas de composé pouvant perturber la mesure, comme du dioxyde de titane, du stéarate de magnésium ou du talc (silicate de magnésium)[41].

Le matériau préalablement réduit en poudre peut aussi être dissout dans un verre: c'est la technique de la perle fondue, la plus complexe, mais qui donne les meilleurs résultats pour des solides hétérogènes[42].
Quant aux liquides, eau, huile, carburant… on les met dans une coupe dont le fond est un film polymère si la mesure se fait par en dessous. On parle d'optique « inversée ». L'analyse se fait sous hélium pour éviter l'ébullition sous l'effet de la chaleur et du vide[43].
Dans le cas d'une optique inversée, le tube et l'analyseur se trouvent sous l'échantillon. Si le film rompt durant l'analyse du liquide, cela peut endommager ces parties ; il convient donc d'adopter un film suffisamment résistant, il faut faire un compromis avec l'absorption des rayons X (puisque plus un film est épais et plus il est résistant) et la présence d'éléments perturbateurs dans le film (qui permettent au film de mieux résister à certains produits). Ce problème ne se pose pas dans le cas des optiques directes (mesure par le dessus), mais le problème est alors de mettre un volume défini de liquide afin que la surface soit au niveau de référence[43].
Le logiciel de traitement des résultats doit prendre en compte la préparation de l'échantillon, à la fois dans l'estimation des effets de matrice, mais aussi pour afficher les concentrations dans l'échantillon initial. L'étalonnage de l'instrument (voir ci-dessous) sera spécifique pour chaque type de préparation.
Élaboration de la recette d'analyse[modifier | modifier le code]
Un opérateur qui veut analyser un échantillon par SFX doit d'abord exprimer son problème, par exemple, mesurer la concentration du chrome dans son échantillon, et ensuite déterminer quelles sont les raies qu'il peut mesurer pour résoudre son problème, et enfin quels sont les paramètres instrumentaux qui donneront les meilleurs résultats.
Choix des raies mesurées[modifier | modifier le code]
Pour la plupart des éléments, l'opérateur a le choix entre plusieurs raies possibles. Les raies mesurables sont en général les raies
- Kα et Kβ pour les éléments légers, jusqu'au potassium (Z = 19) ;
- Kα, Kβ, Lα et Lβ pour les éléments moyens et lourds, du calcium (Z = 20) au lanthane (Z = 57) ;
- les raies K ne sont plus mesurables pour les lanthanides et à partir du tungstène (Z = 74) ;
- la raie Mα est mesurable du hafnium (Z = 72) au bismuth (Z = 83).
L'opérateur a à sa disposition des tables qui le renseignent (Voir, sur wikibooks b:Spectrométrie de fluorescence X#Raies caractéristiques des éléments dans le domaine des rayons X). Ces informations sont disponibles en ligne sur un certain nombre de sites[44]. Une raie est mesurable si l'énergie des rayons X du tube est suffisante pour provoquer une ionisation dont la désexcitation provoque l'émission voulue. Par exemple, la raie Kα1 du tantale (Z = 73) a une énergie de 57,6 keV, ce qui signifie qu'il faut une tension d'accélération du tube supérieure à 57,6 kV (57 600 V). Les tubes et leur électronique d'alimentation sont souvent limités à 60 kV.
Pour les appareils dispersifs en longueur d'onde, la longueur d'onde de la radiation doit donner un angle de diffraction dans la limite des butées du goniomètre de l'appareil. Quel que soit le goniomètre, la longueur d'onde doit être inférieure au double de la distance interréticulaire du cristal analyseur 2d. Par ailleurs, si la déviation est très faible, le faisceau s'étale sur le cristal analyseur et le détecteur reçoit une portion plus faible du signal. Par exemple, pour un cristal LiF200, la longueur d'onde doit être supérieure à 0,285 nm (2,85 Å) soit une énergie minimale de 4,4 keV, et si l'on considère que la déviation minimale exploitable est 10 °, cela correspond à une longueur d'onde de 0,049 nm (0,49 Å) soit une énergie maximale de 25,3 keV.
Le rendement du détecteur doit être suffisant pour l'énergie concernée. Les plages typiques d'utilisation sont :
- détecteur à semi-conducteur : 1 keV à 50 keV, (longueurs d'onde de 12 Å à 0,25 Å), avec une plage optimale entre 1,6 keV et 24,8 keV ;
- scintillateur : 3 keV à 60 keV (longueurs d'onde de 4 Å à 0,2 Å), avec une plage optimale entre 6 keV et 40 keV (2 à 0,3 Å) ;
- compteur proportionnel à gaz : 0,18 keV à 50 keV (longueurs d'onde de 70 Å à 0,25 Å), avec une plage optimale entre 0,25 et 8,3 keV.
Dans la pratique, les différents types de détecteurs ne sont pas disponibles sur un même instrument. Les instruments EDS sont équipés exclusivement de détecteurs à semi-conducteur. La contrainte d'un détecteur adapté à une analyse donnée peut conduire au choix de l'instrument, mais le détecteur présent sur l'appareil à disposition de l'opérateur conduit également ce dernier à sélectionner l'une des raies parmi plusieurs possibles.
D'autres phénomènes, qui dépendent de la composition de l'échantillon, entrent en ligne de compte dans le choix de la raie :
- la proximité de raies voisines (superposition de raies, interférences), on peut ainsi préférer, pour un élément, une raie ayant un rendement moins bon mais qui n'est pas perturbée ;
- la profondeur analysée : une raie peu énergétique a une profondeur de pénétration faible, la couche superficielle doit donc être représentative de l'échantillon ce qui rend la préparation critique (problématique similaire à celle de l'échantillonnage) ; une raie très énergétique pénètre profondément, donc le signal est une moyenne sur un volume important, mais si l'échantillon est trop mince, l'hypothèse de « l'épaisseur infinie » n'est plus valable ;
- le bruit de fond : certaines zones ont plus de bruit de fond que d'autres (par exemple proximité des raies caractéristiques du tube diffusées par effet Rayleigh et Compton).
Choix des conditions de mesure[modifier | modifier le code]
Une fois la raie choisie se pose la question des conditions de mesure, et tout d'abord du type d'appareil : appareil dispersif en longueur d'onde ou en énergie ? Ce choix se fait au moment de l'achat de l'appareil, on choisit l'appareil en fonction des applications prévues, mais aussi du coût et de l'infrastructure requise (espace, alimentation en fluides).
Quelle excitation du tube ? la puissance du tube étant limitée (typiquement 1 à 4 kW pour un appareil dispersif en longueur d'onde), il faut donc trouver un bon rapport tension/intensité. Une raie très énergétique nécessite une tension d'accélération forte pour exciter l'élément ; une raie peu énergétique a un mauvais rendement, il faut donc favoriser l'intensité du courant d'excitation aux dépens de la tension (de fait, la tension peut être faible puisque l'énergie d'excitation l'est aussi). Il faut considérer présence éventuelle d'un filtre pour couper les raies caractéristiques du tube, et donc réduire l'effet Rayleigh et Compton qui peuvent perturber la raie mesurée (augmentation du bruit de fond) ;
Pour les appareils dispersifs en énergie (EDS) se pose la question du choix des paramètres de traitement du signal, favorisant la résolution (pouvoir de séparation) ou l'intensité (limite de détection). Pour les appareils dispersifs en longueur d'onde se pose systématiquement la question du choix du cristal et du collimateur qui peut, selon la réponse qui est faite, favoriser la résolution spectrale ou au contraire la limite de détection. D'une façon générale, une bonne résolution ira dans le sens de la réduction de l'intensité du signal, et donc de la dégradation de la limite de détection. Le paramétrage du détecteur, et en particulier du discriminateur qui filtre les impulsions, doit faire face à la même contradiction : la résolution en énergie s'oppose à la limite de détection. S'il est possible de choisir le détecteur en analyse WDS, le compteur proportionnel optimisera la mesure des faibles énergies, alors que le scintillateur optimisera les fortes énergies.
La maturité de la technique a dégagé un certain nombre d'applications de routine. Par ailleurs, du fait des progrès du matériel et du logiciel informatique, une part de plus en plus croissante de l'expertise a été transférée de l'opérateur vers le logiciel embarqué avec les appareils de mesure. Le développement d'appareils bon marché a aussi contribué à favoriser l'usage des instruments par un personnel peu qualifié. Bien que certaines applications restent encore du domaine de l'expert, les fabricants d'appareils fournissent des bibliothèques de raies et de conditions de mesure toutes faites pour les principales applications, l'utilisateur « n'ayant plus qu'à » choisir parmi les conditions préétablies. Une partie de l'expertise enfouie dans l'instrument réside dans la façon dont l'appareil est étalonné en usine.
Étalonnage[modifier | modifier le code]
En introduction à sa contribution sur les méthodes de standardisation utilisées en SFX, Mauser applique à la fluorescence X l'adage de métrologie souvent cité pour toutes sortes de techniques de mesures : « X-Ray fluorescence is the best method to get wrong results in a perfectly reproducible way »[45]. En fait, comparé à d'autres techniques, la SFX repose sur un corpus théorique suffisamment opérationnel pour que des instruments simplement réglés en usine donnent des résultats « pas si faux que ça ».
Étalonnage d'usine (méthodes dites « semi-quantitatives » ou « sans étalon »)[modifier | modifier le code]
Grâce aux méthodes de correction de matrice par les paramètres fondamentaux, il est possible de faire un étalonnage « universel » de la machine en usine. Le terme « universel » signifie qu'il est indépendant du type d'échantillon à condition que les hypothèses physiques faites lors du développement de l'étalonnage soient respectées[45]. Dans le cas général, ces hypothèses sont :
- l'homogénéité de l'échantillon ;
- l'exhaustivité qui implique que tous les éléments sont mesurés ou estimés par stœchiométrie ou par complément à 100 %.
En général, l'étalonnage est fait par le constructeur sur un appareil de référence. C'est un étalonnage qui comporte peu de points par élément, éventuellement même un seul point : il s'agit de déterminer la sensibilité du système pour une raie donnée. L'étalon est souvent fait de l'élément pur ou de son oxyde pur.
L'étalonnage doit ensuite être transposé sur l'appareil final, pour prendre en compte les différences avec l'appareil de référence. Pour cela, on dispose d'un jeu d'échantillons stables (en général des verres) qui sont mesurés sur l'appareil de référence et sur l'appareil final ; le rapport des intensités mesurées sur les deux appareils est appliqué aux coefficients d'étalonnage.
On désigne souvent ces méthodes de :
- méthodes « semi-quantitatives » (« semiquant » en abrégé) : en effet, l'échantillon ne respectant pas nécessairement les hypothèses émises, la précision ne peut être garantie (lorsque l'on développe un étalonnage spécifique, si les étalons ont les mêmes « défauts » que les inconnus, ces défauts sont intégrés dans le coefficient d'étalonnage) ;
- méthodes « sans étalon » (« standardless » en anglais)[45], car l'utilisateur n'a pas à préparer d'étalon.
Les deux dénominations sont erronées : si l'échantillon répond aux hypothèses, le résultat est tout à fait précis, et donc pas semi-précis, et les méthodes ont bien été faites à partir d'étalons mesurés en usine.
Étalonnage spécifique[modifier | modifier le code]
Pour de nombreuses applications, l'étalonnage d'usine est insuffisant ou inapproprié : c'est le cas lorsque les hypothèses sous-jacentes ne sont pas valables, par exemple l'échantillon n'est pas homogène mais il est sous forme de poudre, d'une solide cristallisé ou d'un dépôt sur filtre. On peut aussi demander à l'analyse une grande précision, et la simple transposition d'un étalonnage d'une machine sur l'autre ne permet pas d'atteindre cette précision. On veut travailler avec des conditions de mesure différentes de celles utilisées pour l'étalonnage en usine, et ces différences ne sont pas facilement transposables, par exemple lorsque la haute tension du tube est différente. Dans ces cas-là, il faut faire un étalonnage spécifique[45].
Cet étalonnage spécifique requiert de définir explicitement des méthodes de standardisation qui recouvrent aussi bien les préparations d'échantillon que le choix d'échantillon de référence et le protocole de mesure et de traitement des résultats de mesure qui aboutissent à la production des résultats finaux. Le protocole de mesure et de traitement des données comprend notamment, pour la SFX, la détermination et la soustraction du fond continu, la mesure et la correction des dérives instrumentales, la déconvolution effets de recouvrement de pics, la prise en compte d'échantillons de référence contenant l'élément à mesurer ou au contraire ne le contenant pas et la correction des effets de matrice[45].
La plus grande difficulté d'un étalonnage est de définir les étalons, que l'on appelle parfois « étalons externes » par opposition à la méthode de l'étalon interne parfois utilisée pour corriger des effets de matrice ; on peut pour cela utiliser des étalons certifiés fournis d'un organisme référent, faire soi-même ses étalons, ou bien à défaut utiliser des produits inconnus que l'on caractérise par d'autres méthodes, par exemple l'ICP. Les organismes de standardisation organisent également des Round-robins qui consistent à comparer les mesures effectuées par plusieurs laboratoires spécialisés sur le même échantillon. Mauser note que beaucoup de méthodes de standardisation pratiquée par des laboratoires spécialisées permettent d'obtenir les mêmes résultats pourvu que le même protocole soit suivi, mais ne mentionnent ni le biais de mesure ni les résultats détaillés obtenus au cours des round-robin[45].
Facteurs de mérite[modifier | modifier le code]
On attend généralement d'un appareil mettant en œuvre la spectrométrie de fluorescence X qu'il mesure des concentrations. Les facteurs de mérite de l'appareil sont donc ceux qui participent à la qualité métrologique des appareils de mesure : résolution latérale, résolution en profondeur, sensibilité et limite de détection[46].
La résolution latérale et la résolution en profondeur dépendent essentiellement de la source primaire, mais aussi du processus d'interaction rayonnement primaire matière. La sensibilité sera d'autant meilleure que la source est énergétique et qu'il n'y a pas de perte dans le spectromètre. L'implantation des spectromètres par rapport à l'échantillon détermine l'angle solide du rayonnement fluorescent qui sera effectivement capté par la détection. La limite de détection dépend en partie du niveau de bruit de fond du spectre et des techniques de post-traitement dont on dispose pour soustraire ce fond. Il importe aussi, pour que la mesure soit juste, qu'il n'y ait pas d'erreur sur l'identification du pic mesuré et cette dernière dépend en partie de la résolution spectrale, c'est-à-dire du pouvoir de séparation des pics. La résolution spectrale dépend surtout de la nature et de la qualité des spectromètres. Le problème de l'identification des pics est également compliqué par les effets de matrice.
Estimation des éléments légers[modifier | modifier le code]
Les éléments légers (numéro atomique Z faible) sont très difficilement mesurables en fluorescence X :
- le rendement de fluorescence est très mauvais, ils produisent plutôt des électrons Auger ;
- l'énergie des raies est faible, les photons sont facilement absorbés et génèrent donc un faible signal ;
- les raies des éléments sont proches, il est difficile de les distinguer les unes des autres.
Sous vide avec un appareil dispersif en longueur d'onde, on peut mesurer jusqu'au bore (Z = 5), mais il faut un cristal analyseur spécial pour le bore, un pour le carbone et un pour l'azote. Si l'on utilise un gaz (en général l'hélium) pour maintenir une pression sur l'échantillon, on ne peut mesurer que jusqu'au sodium (Z = 11). En général, même sous vide, on estime que pour les éléments plus légers que le sodium, la mesure est très difficile.
Cependant, ces éléments ont une influence importante sur les effets de matrice. Donc, même si l'on ne s'y intéresse pas, il faut pouvoir les estimer. Cela peut se faire :
- par des mesures extérieures : par exemple mesure de CHNS (oxydation du matériau et analyse des gaz ainsi produits : CO2, NOx, H2O, SO2) ou bien mesure par IGA (interstitial gas analysis) ; ces concentrations sont ensuite entrées manuellement au logiciel qui les prend en compte pour les corrections ; on peut envisager de récupérer les concentrations sur une base de données (LIMS)
- en altérant l'échantillon pour éliminer ces éléments, par oxydation (par exemple lors de la fabrication d'une perle fondue) ; on peut connaître la quantité de composés volatils (perte au feu) par pesée, mais pas leur nature ; on aura donc une mesure précise sur l'échantillon calciné, et on pourra calculer les concentrations dans l'échantillon avant calcination, mais cela ne s'applique pas aux éléments légers qui « résistent » à la calcination ;
- en estimant leur concentration par stœchiométrie : si l'on sait que ces éléments sont liés à des éléments plus lourds dans des composés définis, les mesures pour les éléments lourds permettent de calculer la quantité en éléments légers.
Cette dernière technique est beaucoup utilisée pour les oxydes : par exemple on mesure la quantité d'aluminium, et l'on calcule la quantité d'oxygène lié à partir de la formule de l'alumine.
Expression des résultats[modifier | modifier le code]
La spectrométrie de fluorescence X est une méthode d'analyse élémentaire, donc permet de déterminer les concentrations en éléments purs. Cependant, les éléments sont souvent présents sous la forme de composés (molécules, cristaux polyatomiques) dans le matériau initial. Il peut donc être souhaitable de présenter des pourcentages de composés plutôt que d'éléments. On exprime par exemple souvent des concentrations en oxyde, en particulier en géochimie ou pour les ciments.
La concentration en composés est calculée, en général par le logiciel d'analyse, à partir des concentrations en éléments et des formules chimiques. Si l'élément n'est pas présent sous la forme indiquée, alors l'expression en composé est fausse, bien que l'analyse soit juste.
Par exemple, le fer peut être présente sous la forme de fer pur Fe, ou d'oxyde de fer : wustite FeO, hématite Fe2O3, magnétite Fe3O4, mais aussi sulfure : pyrrhotite FeS, marcassite FeS2, ou encore sulfate : sulfate ferreux FeSO4, sulfate ferrique Fe2(SO4)3, … La spectrométrie de fluorescence X ne permet pas de déterminer la forme sous laquelle le fer est lié, et les éléments liés sont en général légers donc non mesurables, l'expression sous la forme d'un composé unique peut donc être fausse.
Ceci peut donner une somme des concentrations inférieure ou supérieure à 100 %.
Différentes formes de l'analyse par fluorescence X[modifier | modifier le code]
Appareils SFX portables (ou pXRF)[modifier | modifier le code]
Il existe depuis 1995 environ des spectromètres portables alimentés sur batteries destinés aux utilisations sur site. Ils ont en général la forme d'une perceuse ou d'un pistolet. Les premiers modèles utilisaient des sources de rayons gamma pour exciter la raie L ou des sources de rayons X pour exciter la raie K. Ces appareils à sources radioactives (109Cd, 241Am ou 55Fe) sont toujours utilisés dans le diagnostic bâtiment pour détecter la présence de plomb dans les peintures ou les canalisations des logements (prévention du danger de saturnisme lié au plomb). Toutefois, depuis 2000, ils sont remplacés pour les autres applications par des spectromètres où la source de rayons X est un tube, en raison des contraintes rigoureuses portant sur l'utilisation des sources radioactives. Les premiers appareils à tubes avaient une précision limitée et étaient de fait plus utilisés pour obtenir des résultats qualitatifs et non destructifs.
Depuis 2005, les progrès techniques sur les spectromètres à tubes, et une meilleure compréhension de la préparation des échantillons, ont permis de rapides progrès, et les spectromètres portables ont des performances leur permettant de réaliser de véritables analyses lorsque les échantillons sont soigneusement préparés[47]. Les limitations en puissance dues aux batteries et au poids les limitent toutefois aux éléments les plus lourds, de masse atomique comprise entre celle du silicium et celle de l'uranium. Les applications concernent le diagnostic environnemental et la dépollution, les activités minières, La collecte sélective et le traitement des déchets, dans l'industrie pour confirmer le type de matériau lors de la fabrication, pour le contrôle des matières premières, mais aussi pour l'analyse non destructive des œuvres d'art, des pièces archéologiques et des végétaux (liste non limitative).
Analyse SFX sur filtre[modifier | modifier le code]
Le cas envisagé ci-dessus était celui d'un échantillon massif (liquide, solide ou pulvérulent). On peut également analyser des dépôts sur filtre.
Les effets de matrice sont des effets de masse ; dans le cas d'une couche très mince et peu dense, il n'y a pas d'absorption (tous les atomes sont en « première ligne ») et la fluorescence secondaire (surexcitation) est négligeable. On travaille donc sans correction de matrice ; l'intensité est directement proportionnelle à la concentration surfacique (en mg/cm2 ou µg/cm2).
Le filtre peut être un papier buvard sur lequel on dépose une solution. En général, le filtre comporte un cercle d'apparence brillant qui empêche la solution de diffuser sur tout le papier mais la circonscrit dans un disque, ce qui permet la reproductibilité des mesures : si l'on met toujours la même quantité de solution, on est sûr d'avoir toujours la même concentration surfacique. On peut donc exprimer les résultats directement en concentration volumique de la solution (mg/L ou µg/L).
La solution peut elle-même être une préparation issue d'un filtre ; par exemple, on filtre de l'air ou des fumées avec une mousse, cette mousse est calcinée (brûlée), et le calcinat est mis en solution et déposé sur le filtre.
Le filtre peut également être directement un filtre à poussière, mais il se pose alors le problème de la tenue mécanique des particules de poussière.
Les analyses sur filtre revêtent une grande importance pour la surveillance des conditions de travail (prévention des maladies professionnelles, notamment surveillance des particules de silice) et la protection de l'environnement (surveillance des rejets de fumées, notamment en métaux lourds).
Spectrométrie en réflexion totale (TXRF)[modifier | modifier le code]

La spectrométrie de fluorescence X en réflexion totale, ou TRXRF (total reflection X-ray fluorescence spectrometry), est une méthode permettant d'analyser des quantités de matière très petite. Elle consiste à réduire le bruit de fond en déviant le faisceau incident vers un absorbeur, on ne voit ainsi plus l'effet Rayleigh ou Compton.
Microfluorescence (MicroXRF)[modifier | modifier le code]
Définition[modifier | modifier le code]
La microfluorescence consiste à utiliser un faisceau très fin pour pouvoir analyser une aire très petite. On peut ainsi réaliser une cartographie chimique de l'échantillon.
Application[modifier | modifier le code]
Cette technique a été utilisée en 2014, par le Centre de Recherche sur la conservation des collections (CRCC), pour analyser en particulier, les papiers de la reine Marie-Antoinette, dont sa correspondance secrète avec Hans Axel de Fersen. Les archives de la reine, sont conservées aux Archives nationales sous la cote 440AP, et la consultation se fait uniquement sous forme de microfilms[48].
L'analyse de l'encre des mentions occultées d'une de ses lettres à Hans Axel de Fersen a permis de confirmer les sentiments amoureux qu'elle lui manifestait[49]. En effet, celle-ci a permis de différencier les concentrations de sulfate de cuivre, dans les encres utilisées à l'époque, et d'extraire l'écriture originale de Marie-Antoinette, dont les mentions caviardées, a posteriori.
Dans la lettre analysée et datée du , Marie-Antoinette a précisé : « je vais finire, non pas sans vous dire mon bien cher et tendre ami que je vous aime a la folie et que jamais jamais je ne peu etre un moment sans vous adorer »[50].
Techniques de Spectrométrie de fluorescence X à source primaire autre que les rayons X[modifier | modifier le code]
Il est possible de provoquer un rayonnement caractéristique secondaire X en bombardant avec d'autres radiations :
- en utilisant un faisceau d'électrons, c'est la microsonde de Castaing ;
- en utilisant un faisceau d'ions, c'est la méthode dite sonde nucléaire ou PIXE (particle induced X-ray emission) ;
- en utilisant un rayonnement alpha (Alpha particle X-ray spectrometer).
Lorsque l'on bombarde la matière avec des rayons X, celle-ci émet d'autres rayonnements qui peuvent être utilisés pour l'analyse :
Techniques d'analyse voisines[modifier | modifier le code]
XPS, Auger, XANES[modifier | modifier le code]
La méthode dite XPS (X-ray photoelectron spectroscopy) ou ESCA (electron spectroscopy for chemical analysis), utilise, comme la SFX, le rayonnement X comme source primaire, mais elle met en œuvre des électrons éjectés par effet photoélectrique.
La désexcitation provoque également l'éjection d'électrons Auger, mais la spectrométrie Auger (AES, Auger electron spectrometry) utilise un faisceau d'électrons comme rayonnement incident.
Enfin, les rayons X sont absorbés par effet photoélectrique, on peut donc faire de la spectrométrie d'absorption des rayons X (XANES).
Comparaison de la SFX avec les techniques voisines[modifier | modifier le code]
On tire le meilleur parti de la SFX dans l'analyse d'échantillons métalliques[51] ou semi-conducteurs de plusieurs microns d'épaisseur, par exemple pour l'identification d'alliages, et dans ce cas, l'échantillon est introduit dans l'appareil sans préparation spéciale, ou dans l'identification d'échantillons inconnus, solides, liquides ou sous forme de poudre[52].
Lorsqu'on en vient à effectuer des comparaisons entre différentes techniques d'analyse, il devient difficile de considérer toute la famille de spectrométrie par fluorescence X dans son ensemble, si ce n'est pour constater que toutes ces techniques donneront des informations sur la composition chimique des échantillons, mais sont appropriées pour la détermination de rapports isotopiques qui est l'apanage de la spectrométrie en masse. La SFX dont il est question ici s'emploie au sens strict, excluant les variantes EPMA ou PIXE. De la comparaison avec les autres techniques, il ressort que les points forts de l'analyse SFX peuvent être présentés ainsi[52]:
- Non destructivité pour les tranches de semiconducteurs (Wafer) et les échantillons métalliques
- Absence de préparation pour de tels échantillons
- Possibilité d'analyser des zones de 30 micromètres ou moins
- Possibilité d'analyser des liquides et des solides.
- Exploration en profondeur jusqu'à 10 micromètres.
À ces avantages en performances s'ajoute un faible encombrement et un coût de fonctionnement relativement modique ne nécessitant que l'électricité, l'eau de refroidissement (possibilité de circuit fermé avec refroidisseur) et éventuellement gaz argon-méthane (mélange pour détecteur à flux gazeux) et hélium (atmosphère protectrice).
Les inconvénients sont :
- mesure parfois destructrice du fait de la nécessité de prélever un échantillon de taille réduite : la mesure doit se faire en atmosphère contrôlée (vide ou hélium) pour avoir des résultats précis, donc dans une chambre de taille réduite ;
- préparation délicate dans certains cas : les échantillons doivent résister aux faibles pressions ;
Il y a un certain nombre de techniques d'analyse qui permettent la détermination de la composante chimique des éléments. Ces techniques se distinguent les unes des autres par la gamme de concentration couverte, l'information sur la profondeur, la précision etc. Un petit nombre d'entre elles profondeur[53]. Parmi toutes ces techniques, la spectrométrie de fluorescence X est celle qui permet d'obtenir la meilleure réolution spatiale, mais sous sa forme EPMA seulement, et dans ce cas, la résolution en masse peut être meilleure que 100 nanomètres[53]. Sous sa forme PIXE, la résolution spatiale peut être du même ordre de grandeur que le SIMS, c'est-à-dire de quelques dixièmes de µm. Lorsque la source primaire est le rayonnement X, la résolution spatiale ne descend jamais au-dessous de 10 μm. On peut quand même parler d'analyse locale, ce qui n'est pas le cas de la torche à plasma, utilisée en spectrométrie de masse(ICP-MS) ou en spectrométrie optique (ICP-AES). Pour la détection des éléments trace, la SFX peut obtenir de bons résultats, bien meilleure que le ppm, lorsque le rayonnement primaire est celui d'un synchrotron. Ce n'est pas aussi bien que la SIMS ou l'ICP-MS[53].
Mais par rapport à une technique comme le SIMS, le grand avantage de la SFX est son aspect quantitatif, la rapidité de la mesure, puisque plusieurs dizaines d'éléments sont détectables en une seule mesure.
Le prix d'achat était de l'ordre 100 à 150 k€ dans les années 2000 pour un appareil dispersif en longueur d'onde.
Ceci est à comparer à d'autres méthodes d'analyse. En particulier, la torche à plasma, autre méthode multiélément, a une limite de détection bien inférieure (jusqu'au ppb sur une solution diluée avec une ICP-MS, alors que l'on peut au mieux espérer atteindre le ppm dans certains cas en fluorescence X), mais a un coût de fonctionnement bien plus élevé (consommation en « argon U[54] » de la torche à plasma, contrainte des réétalonnages réguliers).
Normes relatives à la fluorescence X[modifier | modifier le code]
Les normes suivantes font appel à la fluorescence X :
- ISO 9516
- détermination par spectrométrie de fluorescence X dispersive en longueur d'onde, dans les minerais de fer ayant une grande perte au feu, des teneurs en fer, silicium, calcium, manganèse, aluminium, titane, magnésium, phosphore, soufre, potassium, étain, vanadium, chrome, cobalt, nickel, cuivre, zinc, arsenic, plomb et baryum ;
- EN ISO 14596
- détermination par spectrométrie de fluorescence X dispersive en longueur d'onde de la teneur en soufre dans les produits pétroliers (type essence, gazole, …), pour des teneurs entre 0,001 %m et 2,5 %m ;
la méthode proposée est une méthode de correction de matrice par étalon interne, le zirconium introduit sous la forme d'octanoate de zirconium ; bien que la méthode de l'étalon interne soit obsolète depuis le développement des algorithmes de paramètres fondamentaux, et peu adaptée à la fluorescence X, elle est ici possible puisque l'on a un produit liquide et une raie du zirconium proche en énergie d'une raie du soufre sans qu'il y ait de superposition (la raie S-Kα est à 0,537 3 nm et la raie Zr-Lα1 est à 0,607 0 nm) ; elle permet de ne mesurer que deux raies, quels que soient les autres éléments présents ;
les étalons sont des solutions de dibenzothiophène (DBT), de sulfure didibutylé (DBS) et de thianaphtène (TNA, ou benzothiophène), diluées dans une huile blanche.
- ISO 29581-2
- Cement — Test methods — Part 2: Chemical analysis by X-ray fluorescence
- Analyse des ciments par spectrométrie de fluorescence X.
(X31-013)
Qualité du sol - Analyse rapide d'une sélection d'éléments dans les sols à l'aide d'un spectromètre de fluorescence X à dispersion d'énergie portable ou portatif
Procédure d'analyse rapide d'une sélection d'éléments dans les sols et matériaux similaires lorsque l'on utilise des spectromètres XRF à dispersion d'énergie portables ou portatifs. Cette méthode rapide est supposée être appliquée sur site pour obtenir des données qualitatives ou semi-quantitatives qui aident notamment à décider de la stratégie d'échantillonnage plus poussée pour évaluer la qualité du sol.
Cette norme est la première proposée par l'AFNOR (en France) et l'ISO pour l'utilisation des spectromètres de fluorescence X portables pour les applications environnementales. Délibérément prudente, elle ne couvre que les développements validés de la méthode. Pour les développements ultérieurs, il est nécessaire de s'appuyer sur la littérature scientifique[55], en rapide développement depuis 2015.
Standard Guide for Elemental Analysis by Wavelength Dispersive X-Ray Fluorescence Spectrometry
Ce guide fournit des directives pour la mise au point et la description de procédures analytiques utilisant un spectromètre à rayons X à dispersion de longueur d'onde pour l'analyse élémentaire de métaux solides, de minerais et de matériaux connexes. Les formes matérielles discutées ici comprennent les solides, les poudres et les formes solides préparées par des procédés chimiques et physiques tels que la fusion au borate et le pressage de briquettes.
Standard Practice for Quality Systems for Conducting In Situ Measurements of Lead Content in Paint or Other Coatings Using Field-Portable X-Ray Fluorescence (XRF) Devices
Cette norme couvre la collecte et la documentation de mesures de contrôle de la qualité permettant de déterminer des niveaux de performance instrumentale acceptables lors de l'utilisation de spectromètres de fluorescence de rayons X à dispersion d'énergie portables sur le terrain, afin de générer des résultats de classification du plomb à partir de mesures sur peinture et d'autres films de revêtement dans les bâtiments et les structures connexes.
Elle couvre le domaine historique de développement des spectromètres de fluorescence X portables, qui est celui de la détection du plomb dans l'habitat pour les applications sanitaires, et plus particulièrement dans les peintures.
- ASTM C-114
- certification des analyses de ciments hydrauliques par spectrométrie de fluorescence X ;
le laboratoire doit préparer, deux jours différents, des perles fondues à partir de matériaux de référence (standard reference materials, SRM) du NIST, et calculer la moyenne et la différence des teneurs ;
la méthode est validée si- l'erreur systématique (accuracy), c'est-à-dire la différence entre la moyenne et la valeur certifiée du matériau, est inférieure à une valeur donnée, par exemple 0,03 %m pour le dioxyde de titane (TiO2), 0,1 %m pour les oxydes de fer (Fe2O3) et de soufre (SO3), 0,2 %m pour la silice (SiO2) et l'alumine (Al2O3), 0,3 %m pour la chaux (CaO) ;
- la dispersion statistique (précision), c'est-à-dire la différence entre les deux mesures, est inférieure à une valeur donnée, par exemple 0,02 %m pour le dioxyde de titane, 0,1 %m pour l'oxyde de soufre et 0,2 %m pour l'alumine.
Notes et références[modifier | modifier le code]
- Heinrich 1981, p. 59-60
- J. Despujols, Historique de l'analyse par fluorescence X, Journal de Physique IV, Colloque C4, supplément au Journal de Physique Iü, Volume 6, juillet 1996 pdf en ligne
- Quintin M., « Qui a découvert la fluorescence X ? », Journal de Physique IV, Colloque C4, supplément au Journal de Physique Iü, Volume 6, juillet 1996
- Jean-Christophe Pain, « Fluorescence X et dénomination K, L, M... des couches électroniques », Bulletin de l'union des physiciens, vol. 112, no 1008, , p. 1161-1167 (lire en ligne)
- Jean-Christophe Pain, « Georges Sagnac : de la découverte de la fluorescence X à la relativité », Histoire de la recherche contemporaine, t. IX, no 2, , p. 180-188 (lire en ligne)
- « Histoire »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (UPENN)
- M. Siegbahn, The spectroscopy of X-Rays, Oxford University Press, London,
- Richard M. Rousseau et Jacques A. Boivin, « The fundamental algorithm : a natural extension of the Sherman equation, part I: Theory », The Rigaku Journal, vol. 15, no 1, , p. 22[(en) lire en ligne]
- John Donovan, Electron Probe Micro Analysis Course, University of Oregon, chapitre 1 [lire en ligne]
- Voir sur la wikipedia anglaise Silicon drift detector
- Heinrich 1981, p. 121
- Roland Akselsson, Short CV for professor Roland Akselsson, Lund University, Sweden[lire en ligne]
- [1](en) « Thermo Scientific NITON® Analyzers History and Background », sur Thermo Scientific Niton XRF Analyzers
- Heinrich 1981, p. 61-66
- Rex Couture, « Intelligent Interpolation for background subtraction - a hybrid approach for trace-element analysis », Advances in X-Ray Analysis, vol. 44, , p. 355-360 ; R. A. Couture et R. F. Dymek, « A reexamination of absorption and enhancement effects in X-ray fluorescence trace element analysis », American Mineralogist, vol. 81, , p. 639-650
- Goldstein et coll. 1992, p. 75, 116-117
- Goldstein et coll. 1992, p. 400, 417
- Goldstein et coll. 1992, p. 424-427, section 9.2.3.
- Goldstein et coll. 1992, p. 744-750, chapitre 14, tableau 14.3
- Heinrich 1981, p. 69
- Heinrich 1981, p. 99-100, 129
- Heinrich 1981, p. 103-110
- Beckoff et coll. 2006, p. 5-6
- Goldstein et coll. 1992, p. 273-280, section 5.2
- Note d'application de Cameca, SX 100 Crystals and their wavelength coverage, 2002 pdf en ligne
- Heinrich 1981, p. 121-122
- C'est une valeur moyenne empirique pour le silicium qu'il ne faut pas chercher à relier au gap de 1,12 eV. Voir par exemple Fabri et al. Energy for Electron-Hole Generation in Silicon by α Particle, Phys.Rev, 131-1, 1 jul 1963
- Goldstein et coll. 1992, p. 310-313
- Goldstein et coll. 1992, p. 331-337, section 5.4
- Goldstein et coll. 1992, p. 283-289, section 5.2.3
- Ruste 1978, p. 226-242
- Ruste 1978, p. 242-258
- Beckoff et coll. 2006, p. 221-222
- Goldstein et coll. 1992, p. 296-304, section 5.3.2
- Heinrich 1981, p. 119
- Goldstein et coll. 1992, p. 283, section 5.2.2
- Goldstein et coll. 1992, p. 296, section 5.3.2
- Beckoff et coll. 2006, p. 228
- Zeev B. Alfassi, Instrumental multi-element chemical analysis, Springer, 1998, (ISBN 0751404276), p. 309
- Beckoff et coll. 2006, p. 411-426
- Beckoff et coll. 2006, p. 421-424
- Beckoff et coll. 2006, p. 424-425
- Beckoff et coll. 2006, p. 411-415
- Par exemple, Jeffrey B. Kortright and Albert C. Thompson, Photon energies, in electron volts, of principal K-, L-, and M-shell emission lines table 1-2, en ligne dans X-Ray Data Booklet, Center for X-ray Optics and Advanced Light Source, Lawrence Berkeley National Laboratory le booklet, en ligne
- K-E Mauser, Standardized Methods dans Beckoff et coll. 2006, p. 400-407
- pour la SFX, on peut se reporter à R. Jenkins et J. V. Gilfrich, « Figures-of-Merit, Their Philosophy, Design and Use », X-Ray Spectrometry, vol. 21(6), , p. 263-269
- Valérie LAPERCHE, « OUTILS DE MESURE SUR SITE : QUEL BESOIN ET QUELLES MESURES POUR QUELLE UTILISATION ? », Rapport ADEME, , p. 6 (lire en ligne)
- 440AP. Marie-Antoinette (papiers) : 1770-1804 - Archives nationales
- Les dessous des lettres de Marie-Antoinette, LE MONDE, 11.01.2016, par Vahé Ter Minassian
- Centre de Recherche sur la Conservation, « Les passages cachés des lettres de Marie-Antoinette au comte de Fersen livrent leurs premiers secrets » [PDF], sur crc.mnhn.fr, (consulté le ).
- « Analyse des matériaux par spectrométrie de fluorescence X », sur MetalBlog,
- Selon le site dEvans Analytical Group, laboratoire de service proposant des analyses de toutes sortes site EAG
- B.Kanngisser et M.Haschke, section 7.1.2 dans Beckoff et coll. 2006, p. 434-436
- argon d'ultra-haute pureté
- (en) « A review of pXRF (field portable X-ray fluorescence) applications for applied geochemistry », Journal of Geochemical Exploration, vol. 188, , p. 350–363 (ISSN 0375-6742, DOI 10.1016/j.gexplo.2018.02.006, lire en ligne, consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- [Beckoff et coll. 2006] B. Beckhoff, B. Kanngießer, N. Langhoff, R. Wedell et H. Wolff, Handbook of Practical X-Ray Fluorescence Analysis, Springer, (ISBN 3-540-28603-9, lire en ligne)
- Jacques Despujols, « Application de la spectrométrie des rayons X au dosage des faibles teneurs de métaux dans les minerais », Le Journal de physique et le radium. Physique appliquée, vol. 13, , p. 31A-41A [(fr) lire en ligne]
- J.-P. Eberhart, Méthodes physiques d'étude des minéraux et des matériaux solides, Paris, Doin,
- J.-P. Eberhart, Analyse structurale et chimique des matériaux 2e éd., Dunod, , 614 p. (ISBN 978-2-10-003367-6)
- W. T. Elam, B. D. Ravel et J. R. Sieber, « A new atomic database for X-ray spectroscopic calculations », Radiation Physics and Chemistry, vol. 63, , p. 121–128
- [Goldstein et coll. 1992] (en) J. Golstein, D.E. Newbury, D.C. Joy, C.E. Lyman, P. Echlin, E. Lifshin, L. Sawyer et J.R. Michael, Scanning electron Microscopy and X-Ray Microanalysis : a text for biologists, materials scientists, and geologists, New York/London, Plenum press, , 820 p. (ISBN 0-306-44175-6)
- [Heinrich 1981] Kurt F. J. Heinrich, « The physics of X-Ray », dans Electron beam X-Ray Microanalysis, Van Nostrand Reinhold Company, (ISBN 978-0442232863)
- Ron Jenkins, Fluorescence spectrometry 2nd ed., New York, Wiley-Interscience,
- [Ruste 1978] Jacky Ruste, « Spectromètre de rayons X », dans Microanalyse et Microscopie à balayage, Les éditions de la physique,
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (en) X-ray based methods of analysis, K. Janssens, Université d'Anvers
- (en) liste de diffusion xrf-l@listserv.syr.edu
- (en) European X-ray Spectrometry Association - interesting links
- (en) XRF support group
- (en) LearnXRF.com
- (en) Australian X-ray Analytical Association (AXAA)
- (en) PyMCA, projet libre de l'ESRF pour l'exploitation des données de fluorescence X
- (en) X-Ray Fluorescence Laboratory, téléchargement de logiciels gratuits de l'AIEA
- (en) X-Ray Interactions With Matter


