Focalisation (optique)
En optique, la focalisation est l'opération qui consiste à concentrer des rayons provenant d'un point en un autre point, à l'aide de miroirs, de lentilles ou d'autres éléments optiques.
Le terme « focalisation » a la même racine étymologique que foyer : en faisant converger des rayons lumineux en un point, on obtient une zone très éclairée faisant penser à un feu. Dans le cas de la focalisation d'un faisceau parallèle (faisceau collimaté ou bien lumière réfléchie par un objet lointain), le point de concentration se trouve dans le plan focal du système optique, et si de plus les rayons sont parallèles à l'axe optique du système, ce point est le foyer du système. Des travaux récents ont montré qu'on peut aussi focaliser l'obscurité, avec de résultats qui ne sont pas tout à fait l'inverse de la focalisation de rayons lumineux ou d'autres types d'ondes.
Intérêt de la focalisation[modifier | modifier le code]
La focalisation consiste à obtenir une image nette d'un objet. Le terme « image » est à prendre au sens large d'information caractéristique sur l'objet[évasif].
Il existe deux types de phénomènes pour lesquels la focalisation est utile :
- dans le cas de la diffraction, par exemple pour l'analyse par diffraction sur un cristal, ou bien pour l'analyse spectrale par dispersion de longueur d'onde ;
chaque point du cristal diffractant émet dans toutes les directions, et on veut collecter tous les rayons ayant la même déviation ; il faut donc concentrer ces rayons, quel que soit leur point d'origine, en un même point ;[Information douteuse]
- en photographie et en astronomie, on veut observer des objets proches ou bien très éloignés (en général des étoiles dans le second cas) ;
pour les objets lointains, les rayons (lumineux, radio ou rayons X) qu'émettent ces objets arrivent parallèles, le fait de collecter ces rayons sur une grande surface puis de les concentrer en un point donné permet d'avoir plus de signal.
Dans le cas de la focalisation de rayons parallèles, les rayons se concentrent dans un plan nommé plan focal. Chaque point du plan focal représente une direction de rayons. Le plan focal représente un espace dual de l'espace réel.
Caustique[modifier | modifier le code]

Les systèmes optiques n'étant pas parfaits, dès que l'on s'éloigne des conditions de Gauss la focalisation ne se fait plus en un point unique mais sur une caustique.
Image de la chambre noire[modifier | modifier le code]
Il est difficile d'illustrer le sujet avec des figures à la fois claires (objets proches pour avoir une échelle raisonnable) et géométriquement exactes (déviation des rayons). Les illustrations de cette partie sont donc à considérer comme des schémas explicatifs similaires à ceux que l'on tracerait à main levée sur un tableau.
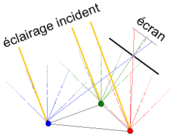
Une expérience simple pour comprendre la focalisation est le principe de la chambre noire : il s'agit d'une boîte dont un des côtés est percé d'un trou, et dont l'autre constitue un écran. Les rayons frappants un objet (venant du Soleil, d'une ampoule…) sont réfléchis par chaque point de l'objet dans toutes les directions (diffusion), donc un point de l'espace (notamment celui où est situé le trou de la chambre noire) reçoit des rayons provenant des différents points de l'objet. Par contre, tous les rayons lumineux frappant l'écran passent nécessairement par le trou, on en conclut donc que chaque point de l'écran reçoit des rayons ne provenant que de la direction du trou.
Supposons que l'on fasse maintenant deux trous, et qu'un miroir dévie les rayons passant par chaque trou, l'écran se trouvant alors entre les trous. En positionnant bien les miroirs, on peut arriver à faire converger les rayons provenant d'un même point de l'objet observé sur un unique point de l'écran. Ainsi, on aura deux fois plus d'intensité. Par contre, il n'est pas possible de faire converger strictement tous les rayons. Certains points seront légèrement dédoublés, on aura comme deux images légèrement décalées, un flou. On voit donc que la focalisation est un compromis entre l'intensité lumineuse et la netteté.
Le fait d'adapter le système pour faire converger au mieux les rayons s'appelle la « mise au point ». D'une manière générale, on arrive à avoir une image nette d'un objet parallèle au plan contenant les deux trous, et il faut adapter la position des miroirs en fonction de la distance de l'objet à la chambre noire. La partie de l'espace donnant une image nette est appelée la « profondeur de champ ».
Si maintenant on n'a pas deux points mais toute une ouverture, il faut un miroir courbe correspondant à des petits miroirs plans mis côte-à-côte. Dans ce cas, on focalise des rayons provenant d'un objet proche par un miroir. Pour l'imagerie d'un objet proche, cette situation n'a actuellement que peu d'application concrète, car il faudrait pouvoir déformer le miroir pour s'adapter à la position de l'objet, et notamment à sa distance de l'objectif (on retrouve le problème du flou). Ce système est toutefois utilisé pour un objet de curiosité vendu dans les magasins de découverte scientifique ou de « farces et attrapes » : il s'agit d'une boîte tapissée d'un miroir courbe sur lequel on pose un objet ; les rayons sont focalisés sur l'ouverture de la boîte, ce qui fait que lorsque l'on regarde le miroir, on a l'impression que l'objet se trouve au-dessus de l'ouverture, suspendu dans le vide, et insaisissable. Par contre, les miroirs courbes sont utilisés pour focaliser les objets situés « à l'infini », par exemple dans les télescopes (voir ci-dessous).
Dans le cas de la chambre à deux trous, on peut aussi dévier les rayons à l'aide d'un prisme. Le résultat est sensiblement le même : on a un gain de luminosité au prix d'un léger flou, les rayons ne convergeant pas tous exactement.
Si l'on met des trous côte-à-côte de manière continue, il faut remplacer les prismes par un prisme courbe, c'est-à-dire une lentille.
Focalisation de rayons provenant de l'infini[modifier | modifier le code]
Dans le cas des instruments d'optiques, l'image donnée par l'objectif est en général observée via un oculaire, dont le but est de donner une image « à l'infini » (cela permet à l'œil de relâcher les muscles chargés de l'accommodation, ce qui présente un meilleur confort d'observation). Si l'objectif focalise la lumière, l'instrument est globalement afocal.
Principe et intérêt[modifier | modifier le code]

Lorsqu'un système optique observe des objets qui sont proches, les rayons lumineux provenant d'un objet ne sont pas tous parallèles, et des rayons parallèles ne proviennent pas nécessairement d'objets qui sont dans la même direction (par rapport à l'axe optique).
En revanche, lorsque les objets sont très éloignés comme des astres dans le ciel, alors les rayons issus d'un point et qui arrivent dans le système optique sont tous parallèles entre eux, et leur direction est la direction de l'objet par rapport au centre optique. On peut le constater de manière simple : si l'on ferme un œil puis l'autre, ou si l'on se déplace d'un pas dans n'importe quelle direction, on voit toujours les astres au même endroit. Cela prouve bien que ce qui importe, c'est la direction observée et non pas le positionnement de l'observateur à quelques mètres près (ce qui n'est pas le cas pour les objets proches de l'observateur).

Ainsi, en sélectionnant une direction de rayons, on sélectionne aussi une direction dans le ciel, donc un objet.
Donc, si l'on met un écran sur le plan focal d'une lentille ou d'un miroir courbe, chaque tache correspondra à la lumière captée venant d'une même direction donc venant d'un même objet (ou d'objets alignés). Plutôt que de mettre un écran, on met en général un miroir, qui prend moins de place et permet de rallonger le trajet optique, donc l'agrandissement de l'image. Plus l'ouverture de l'instrument d'optique est grand, plus on collectera de lumière, plus l'intensité sera importante, mais plus on s'éloignera des conditions de Gauss, moins la focalisation sera parfaite (image floue).
Par ailleurs, si un obstacle bouche partiellement l'ouverture de l'instrument d'optique, cela va diminuer l'intensité visualisée, mais n'altèrera pas l'image, puisqu'il suffit de prendre des rayons venant à côté de l'obstacle (n'oubliez pas que seule la direction des rayons compte). Ainsi, la présence d'un petit miroir devant l'ouverture du grand miroir dans les télescopes de Newton et de Cassegrain ne gêne pas la formation de l'image. La présence du capteur devant le miroir d'une parabole de télévision ne gêne pas la réception des ondes. Par contre, on arrête les rayons passant à proximité du centre optique, on s'éloigne donc des conditions de Gauss, l'image est donc légèrement plus floue.
Exemples[modifier | modifier le code]
Télescopes optiques[modifier | modifier le code]
Les télescopes utilisent des miroirs paraboliques ou sphériques pour focaliser la lumière provenant des astres. Comme le plan focal se trouve devant le miroir focalisateur, donc sur le trajet des rayons arrivant, les rayons réfléchis sont déviés par un autre miroir, ce qui permet d'avoir une image du plan focal du premier miroir. Cette image du plan focal est observée grâce à un dispositif optique appelé oculaire.
Dans le cas des télescopes dits de Schmidt-Cassegrain, le premier miroir est percé en son centre, les rayons sont renvoyés derrière le miroir à travers le trou. Le second miroir, hyperbolique, est perpendiculaire à l'axe optique du télescope.
Dans le cas des télescopes dits de Newton, les rayons sont renvoyés sur le côté par un miroir plan incliné à 45 ° par rapport à l'axe optique du premier miroir.
-
Schéma de principe du télescope de Cassegrain
-
Schéma de principe du télescope de Newton
Lunettes astronomiques, longues-vues et jumelles[modifier | modifier le code]

Dans une lunette astronomique, une longue-vue ou des jumelles, la focalisation se fait avec une lentille convergente. Les rayons frappant la lentille avec un angle donné convergent tous vers un point du plan focal. Ainsi, de même qu'avec un miroir parabolique ou sphérique, les points lumineux du plan focal représentent l'intensité reçue en fonction de la direction des rayons d'origine. On place également un oculaire derrière la lentille de focalisation afin de former l'image dans l'œil de l'observateur.
Télescopes à rayons X[modifier | modifier le code]

Du fait de leurs caractéristiques, les rayons X sont habituellement diffractés ou absorbés par la matière. Toutefois, si l'angle d'incidence est important (incidence rasante, le rayon est presque parallèle à la surface), on a de la réflexion totale. Cette propriété permet de focaliser les rayons X avec un miroir parabolique. L'incidence devant être rasante, on ne peut pas utiliser la partie du miroir proche de l'axe optique (l'incidence est quasiment normale à cet endroit). On utilise un anneau du paraboloïde de révolution et non une calotte.
On peut ainsi faire des télescopes à rayons X afin de capter ces longueurs d'onde émises par les étoiles et autres objets célestes. Les rayons X étant absorbés par l'atmosphère terrestre, de tels télescopes sont embarqués dans des satellites, comme Chandra (NASA) et XMM-Newton (ESA).
Voir aussi Astronomie des rayons X et Télescope Wolter.
Focalisation de rayons provenant d'un objet proche et étendu[modifier | modifier le code]
On cherche fréquemment à avoir une image d'un objet proche et étendu. C'est le cas par exemple de la photographie et de la microscopie.
Un des paramètres importants est la distance de l'objet observé à l'objectif, ou plutôt à son plan focal. C'est tout le problème de la mise au point et de la profondeur de champ.
Mais la focalisation intervient aussi dans d'autres méthodes d'observation :
- focalisation par une lentille électromagnétique dans un microscope électronique en transmission, pour obtenir le cliché de diffraction.
- focalisation des rayons X par un miroir parabolique dans un diffractomètre.
Analyse spectrale par un réseau courbe[modifier | modifier le code]


Une des méthodes pour décomposer la lumière consiste à la faire diffracter sur un réseau optique plan (c'est ce phénomène qui donne les irisations sur un disque compact). Un réseau plan consiste en de nombreuses lignes parallèles espacées uniformément, chaque ligne diffusant la lumière dans toutes les directions (contrairement au miroir qui ne réfléchit un rayon donné que dans une seule direction). Les interférences à l'infini (c'est-à-dire loin du réseau) font que seules certaines couleurs ressortent dans certaines directions. Ceci permet d'analyser le spectre de la lumière : on regarde l'intensité de la lumière dans telle ou telle direction, on sait que chaque direction correspond à une longueur d'onde donnée. Notamment, cela permet de caractériser certains phénomènes qui émettent de la lumière. Par exemple, le spectre d'une étincelle faite sur un matériau est caractéristique de la composition chimique du matériau.
Cependant, ce système présente deux inconvénients :
- il faut que le flux de lumière qui arrive sur le réseau soit parallèle ;
- le détecteur doit être suffisamment loin pour pouvoir considérer les interférences à l'infini.
Dans de nombreux cas, la source de lumière est ponctuelle (comme dans le cas de l'étincelle). On peut alors utiliser un réseau courbe, sous la forme d'une partie de cylindre (un arc de cercle vu de profil), les traits du réseau étant parallèles aux génératrices du cylindre, et l'on place la source sur le cercle. D'après l'une des propriétés géométriques du cercle, tous les rayons subissant une déviation donnée vont converger vers un même endroit du cercle. Ainsi, si l'on place le détecteur sur un point du cercle, on sait que tous les rayons qui y arrivent ont subi la même déviation, leur interférence est donc similaire à une interférence à l'infini.
On a donc focalisé les rayons. Le cercle de focalisation (celui sur lequel se trouvent le réseau, la source et le détecteur) s'appelle le cercle de Rowland.
Ce principe est également utilisé dans les diffractomètres de rayons X : la source de rayons X est ponctuelle, et l'échantillon est courbe et suit le cercle de Rowland, ou bien est plan et tangentiel au cercle de Rowland (focalisation approchée)
- dans les chambres de Seeman-Bohlin ;
- dans les diffractomètres de poudre à géométrie Bragg-Brentano.
Analyse spectrale par un réseau spiralé[modifier | modifier le code]
Une spirale logarithmique possède la propriété suivante : l'angle entre le rayon et la tangente est constant. Ceci confère des propriétés intéressantes vis-à-vis de la focalisation. On utilise des cristaux courbes avec les rayons X, dans les monochromateurs pour la diffraction X[1], ou pour les appareils multicanaux de fluorescence X.
Focalisation des faisceaux laser[modifier | modifier le code]
La focalisation d'un faisceau laser est assez différente de celle des pinceaux lumineux de l'optique géométrique. En effet, la propagation d'un tel faisceau, et plus généralement ses propriétés de diffraction, suivent les lois spécifiques de l'optique gaussienne. Ceci étant dû à la répartition gaussienne de l'intensité dans le plan transverse (perpendiculaire à la propagation) du faisceau.
Focalisation de l'obscurité[modifier | modifier le code]
Paradoxalement, une étude pilotée par les Prof. Ady Arie et Lev Shemer (de l'Université de Tel-Aviv) conduite avec des chercheurs allemands et américains, publiée dans Applied Physics B. a récemment conclu que l'on peut aussi « focaliser l'obscurité » (concentrer des ondes en un point de l'espace où l’intensité lumineuse sera minimale). La maîtrise de ce phénomène pourrait conduire à des innovations technologiques en optique et en acoustique. Selon les auteurs « la focalisation diffractive sombre n’est pas seulement le phénomène opposé de la focalisation lumineuse, mais qu’elle possède également de nombreuses caractéristiques intéressantes par elle-même. Par exemple, nous avons vu que les emplacements des foyers d’ombre sont différents de ceux des foyers lumineux, et que la déstabilisation du système pouvait entraîner la formation de larges bandes d’obscurité »[2]
Notes et références[modifier | modifier le code]
- (en) Dynamical theory of X-ray focussing spectrometers and monochromators curved to the logarithmic spiral [PDF]
- Administrator, « Des chercheurs de l’Université de Tel-Aviv ont montré qu’on peut focaliser l’obscurité exactement comme on peut focaliser la lumière », sur ami-universite-telaviv.com (consulté le )