Train épicycloïdal
Le train épicycloïdal est un dispositif de transmission mécanique[1]. Il a deux degrés de mobilité, comme le différentiel, c’est-à-dire qu'il associe trois arbres ayant des vitesses de rotation différentes avec une seule relation mathématique : il faut fixer les vitesses de deux des arbres pour connaître celle du troisième.
Ces trains sont souvent utilisés pour la réduction de vitesse du fait des grands rapports de réduction que cette configuration autorise, à compacité égale avec un engrenage simple. Ils sont incontournables dans la conception des hélicoptères (régime de la turbine très élevé, régime du rotor très faible, contrainte de poids). On les trouve également souvent en sortie de moteur électrique (voitures et vélos électriques, visseuses-dévisseuses portatives, actuateurs de précision...), ou encore les winchs et les boites de vitesses robotisées à double embrayage.

Description[modifier | modifier le code]

Généralement constitué d'engrenages (il peut s'agir aussi de galets à friction[2]), un train épicycloïdal comporte les éléments suivants[3] :
- deux arbres coaxiaux, dits « planétaires » (le planétaire intérieur est parfois appelé « soleil », et le planétaire extérieur « couronne ») ;
- des satellites s'engrenant avec les deux planétaires, et tournant autour de leur axe commun ;
- le porte-satellites ;
- la couronne ou bâti.
Explication du nom[modifier | modifier le code]
Le terme épicycloïdal vient de la trajectoire suivant une épicycloïde d'un point des satellites observé par rapport au planétaire intérieur. On observe cependant une hypocycloïde si la référence du mouvement est le planétaire extérieur, qui est souvent fixe dans les réducteurs. Cela correspond donc exactement à ce que voit l'observateur qui regarde évoluer un satellite.
- Description des mouvements relatifs
-
Trajectoire épicycloïdale d'un point attaché à un satellite par rapport au planétaire intérieur[a].
-
Trajectoire en hypocycloïde d'une dent d'un satellite vue depuis le planétaire extérieur[a].
Train épicycloïdal[modifier | modifier le code]
Les différentes configurations[modifier | modifier le code]
Trains plans à axes parallèles[modifier | modifier le code]
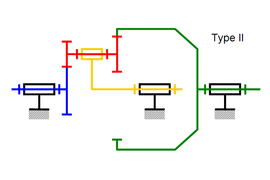
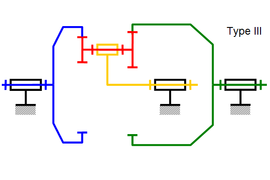
Dans le cas des trains parallèles, les deux planétaires engrenant avec les satellites peuvent être situés autour (cas des planétaires extérieurs), ou au centre (cas des planétaires intérieurs). Il en résulte quatre configurations[4],[3] :
- Différents types de trains épicycloïdaux
-
Satellite à simple denture, un planétaire intérieur et un extérieur.
-
Satellite à double denture, un planétaire intérieur et un extérieur.
-
Satellite à double denture et deux planétaires extérieurs.
-
Satellite à double denture et deux planétaires intérieurs.
Dans tous les cas, les planétaires et le porte satellites ont un axe de rotation commun.
Trains sphériques[modifier | modifier le code]
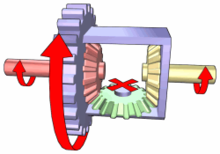
C'est la configuration adoptée dans le différentiel automobile. L'axe de rotation des satellites (souvent par deux) est perpendiculaire à celui des planétaires[5]. De ce fait, les engrenages sont coniques. Les satellites entraînent les planétaires en rotation.
Si les deux planétaires présentent la même résistance à l'effort, les satellites ne tourneront pas. Le couple transmis vers chaque planétaire sera alors le même.
Si la résistance à l'effort est différente, les planétaires se décalent en vitesse (un planétaire tournera plus vite que l'autre) grâce à la rotation des satellites.
Problèmes technologiques[modifier | modifier le code]
- Hyperstatisme (implication sur les liaisons, nombre de satellites).
- Nombres de dents admissibles (critère géométrique, problème de montage en particulier avec satellites à denture multiple).
- Difficulté de représentation sur les dessins d'ensemble.
Applications[modifier | modifier le code]

- Machine à calculer de Blaise Pascal[6] : la pascaline.
- Moyeu à vitesses intégrées des vélos.
- Différentiels de voitures[4].
- La plupart des boîtes de vitesses automatiques d'automobiles et certaines boîtes mécaniques (Ford modèle T par exemple).
- Transmission électro-mécanique type HSD des voitures hybrides (Toyota, Lexus, Ford, Volvo...).
- Multiplicateurs de vitesse de rotation des éoliennes permettant au générateur, qui lui est lié, de fournir la bonne fréquence au réseau électrique.
- Outillage de jardin (broyeurs à meule[7] pour les végétaux par exemple).
- Hélicoptères.
- Turboréacteurs à double flux avec turbosoufflante à engrenages.
Réducteurs épicycloïdaux[modifier | modifier le code]
C'est pour réduire la vitesse de rotation d'un arbre dans un rapport donné qu'on utilise principalement les trains épicycloïdaux. Ils sont présents dans les boîtes de vitesses automatiques et dans de nombreux réducteurs accouplés aux moteurs électriques. Ils figurent d'ailleurs dans les mêmes catalogues que ces derniers. Leur géométrie donne un arbre de sortie coaxial à l'arbre d'entrée, ce qui en facilite la mise en œuvre. Ils ont une grande aptitude à la réduction de vitesse. En général, on dispose trois satellites sur le porte-satellite. Ainsi, les efforts dans les engrenages ne sont pas repris par les paliers. De ce fait, ces réducteurs sont très adaptés à la transmission de couples importants[8],[9],[10],[11]. L'association de moteurs électriques à un moteur thermique fournit une transmission à variation continue telle l'Hybrid Synergy Drive de Toyota.
Ces mêmes dispositifs sont parfois utilisés en multiplicateur, comme sur les éoliennes. Là encore, c'est leur compacité et l'absence d'effort radial induit dans les paliers des arbres d'entrée et de sortie qui en justifie l'emploi. C'est grâce aux améliorations apportées par Mitsubishi Electric en 1982 et les brevets de la société Aisin dès 1996 que GKN et Toyota ont pu développer un système hybride en grande série[réf. nécessaire].
Principe et architecture[modifier | modifier le code]

À partir du train le plus simple (type I), on élimine une mobilité en fixant le planétaire extérieur (ou couronne), par exemple à l'aide d'un embrayage.
L'arbre d'entrée est connecté au planétaire intérieur. En tournant, il force le satellite à rouler à l'intérieur de la couronne. Dans son mouvement, celui-ci entraîne le porte satellite comme s'il s'agissait d'une manivelle. Le porte-satellites constitue l'arbre de sortie du dispositif. Dans cette configuration la sortie tourne dans le même sens et moins vite que l'entrée.
Rapport de transmission[modifier | modifier le code]

1 : bâti (couronne extérieure fixe) ;
2 : arbre d'entrée ;
3 : satellite ;
4 : porte-satellites (arbre de sortie).
Pour un dispositif de transmission de puissance, en particulier les réducteurs, le rapport de transmission constitue la caractéristique principale. Il s'agit du rapport de la vitesse (ou fréquence) de rotation de l'arbre de sortie, sur celle de l'arbre d'entrée. Inférieur à 1 dans les cas d'une réduction, on le remplace souvent par son inverse, le rapport de réduction.
où :
- est le rapport de transmission (adimensionnel) ;
- est le taux de réduction (adimensionnel, souvent indiqué dans les catalogues de constructeurs sous la forme 1:d) ;
- est la vitesse angulaire en rad/s.
Dans le cas présent, le rapport de transmission est donc :
La considération des conditions de non glissement dans les engrenages :
- rotation sans glissement en I entre 2 et 3:
- rotation sans glissement en J entre 1 et 3:
et des propriétés de la liaison pivot entre le satellite et son support donne de plus les relations :
- non glissement en I entre 2 et 3:
- non glissement en J entre 1 et 3: Donc J est centre de rotation de 3 par rapport à 1.
- pivot de centre A entre 3 et 4:
Tous les éléments étant animés d'un mouvement de rotation (permanente ou instantanée) par rapport à 1, on peut écrire les lois de répartition des vitesses, ou champs des vitesses, avec la formule de composition des vitesses. En particulier :
- rotation de 2 autour de O:
- rotation de 4 autour de O:
- rotation de 3 autour de J:
soit :
On peut donc extraire l'expression du rapport :
Dans un engrenage standard, les diamètres sont proportionnels aux nombres de dents (Z) des pignons. En posant la relation de Chasles , avec OI le rayon primitif du planétaire d'entrée, et IA le rayon primitif du satellite, l'expression du rapport de transmission devient :
Avec :
- : la couronne planétaire ;
- : le planétaire ;
- : le satellite.
Par exemple un planétaire de 11 dents attaquant un satellite de 22 dents, donc deux fois plus gros, constitue un réducteur avec un rapport de réduction de 6. Cela est possible avec un engrenage classique que si la roue réceptrice est six fois plus grosse que le pignon d'attaque. À titre de comparaison, si on prend un engrenage classique avec le même pignon d'attaque (à 11 dents) l'encombrement radial de ce réducteur est de 77 dents (11+66) alors que le train épicycloïdal n'occupe que 55 dents (11+2×22), sans compter les problèmes de guidage liés aux efforts induits.
- Note
- l'encombrement réel est obtenu en multipliant le nombre de dents par le module de denture adopté.
Le résultat précédent peut être retrouvé à l'aide de la formule de Willis :
Avec :
- ba : Bâti ;
- pe : Planétaire extérieur ;
- pi : Planétaire intérieur ;
- ps : Porte-satellite ;
- : Nombre de contacts extérieurs dans les engrenages ;
- : Nombre de dents des roues menantes ;
- : Nombre de dents des roues qui sont menées.
Étages de réduction[modifier | modifier le code]

Ces réducteurs sont souvent constitués de plusieurs trains épicycloïdaux mis en cascade. L'arbre de sortie d'un réducteur devient l'arbre d'entrée du suivant. Le rapport global étant alors le produit des rapports intermédiaires, on on peut atteindre dès trois étages des réductions de rapport supérieur à 100, et dès quatre étages des réductions de l'ordre de 1000. Par exemple, avec quatre étages au rapport 1⁄6, on obtient une réduction de 1 296.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Fixe (car choisi comme référentiel).
Références[modifier | modifier le code]
- Informations lexicographiques et étymologiques de « épicycloïdal » (sens b) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- René Champly et al., Eléments des constructions de machines, Paris et Liège, Libr. Polytechnique Ch. Béranger, coll. « Nouvelle encyclopédie pratique des constructeurs », , « Les mécanismes », p. 213-216.
- S. Calloch, J. Cognard et D. Dureisseix, Les Systèmes de Transmission de Puissance : Systèmes mécaniques et hydrauliques, Paris, Hermes Science Publications, , 344 p. (ISBN 2746206692)
- P. Arquès, Transmissions Mécaniques de Puissances, Application aux Boîtes de Vitesses Automatiques, Paris, Ellipses, 2001., p. 278
- Ch. Laboulaye, Traité de Cinématique : ou Théorie des mécanismes, Paris, Libr. E. Lacroix, (réimpr. 1874, 3e), Livre III: combinaison des vitesses, ou mouvements différentiels, « Mouvement circulaire en mouvement circulaire », p. 482
- Pierre Gallais, « Une dent entraîne une dent! », sur Images des mathématiques (CNRS), .
- René Champly et al., Eléments des constructions de machines, Paris et Liège, Libr. Polytechnique Ch. Béranger, coll. « Nouvelle encyclopédie pratique des constructeurs », , « Les mécanismes », p. 216-217
- (en) Hsu, J. S., C. W. Ayers, and C. L. Coomer. [PDF] Report on Toyota/Prius motor design and manufacturing assessment, United States. Department of Energy, 2004.
- (en) Robert Kaczmarek, « Simulating the Toyota Prius Electric Motor »., magneticsmag.com
- (en) Hsu, J. S., et al. [PDF] « Report on Toyota/Prius motor torque-capability, torque-property, no-load back EMF, and mechanical losses », United States Department of Energy, 2004.
- (en) Hsu, J. S., et al. [PDF] « Report on Toyota/Prius Motor Torque Capability, Torque Property, No-Load Back EMF, and Mechanical Losses, Revised May 2007 », no ORNL/TM-2004/185, Oak Ridge National Laboratory (ORNL), Oak Ridge, TN, 2007.

![Trajectoire épicycloïdale d'un point attaché à un satellite par rapport au planétaire intérieur[a].](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e1/Epicycloid1.gif/248px-Epicycloid1.gif)
![Trajectoire en hypocycloïde d'une dent d'un satellite vue depuis le planétaire extérieur[a].](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6e/Hypocycloid1.gif/253px-Hypocycloid1.gif)