Mode (musique)
Le mode, en musique, est un type d'échelle musicale couplé avec un ensemble de comportements mélodiques caractéristiques, notamment en relation avec une note de référence (appelée « finale », « tonique », « note nominale » ou tout simplement « note de référence »). Le terme « mode » a été utilisé dans la théorie musicale occidentale depuis le Moyen Âge pour désigner des caractéristiques :
- du chant grégorien ;
- de la polyphonie de la Renaissance ;
- de la musique tonale.
Au XXe siècle, sa signification a été étendue pour décrire des caractéristiques de musiques de Méditerranée orientale tel que le maqâm, puis d'Asie : râga indien, dastgâh perse, pathet javanais, cho japonais, tyao chinois, etc.[1].
Il est utilisé aujourd'hui aussi dans la théorie de musiques occidentales modernes, notamment du jazz.
La musique modale[modifier | modifier le code]
La musique modale est généralement conçue aujourd'hui en référence aux échelles modales.
Les applications et les principes théoriques qui régissent l'utilisation de ces échelles diffèrent selon les époques et les endroits. Par exemple, la manière dont ces échelles étaient pensées et utilisées dans le plain-chant au Moyen Âge diffère sensiblement de la pratique moderne.
Historiquement, la pratique modale ancienne a été abandonnée entre la fin de la Renaissance et la mort de Bach pour laisser place au système tonal fondé sur deux modes exclusifs — les modes majeur et mineur.
La pratique modale a été redécouverte et adaptée aux principes harmoniques modernes au cours du XIXe siècle.
La musique modale ancienne[modifier | modifier le code]
Le plain-chant médiéval était fondé sur l'utilisation de quatre modes qui se déclinaient sous deux formes : la forme authente et la forme plagale, à savoir les modes de ré (Protus), de mi (Deuterus), de fa (Tritus) et de sol (Tetrardus)[2]. La musique modale a évolué au cours du Moyen Âge et de la Renaissance et fut utilisée au sein de structures contrapuntiques de plus en plus complexes. Au cours du XVIIe siècle les modes sont tombés en désuétude au profit de deux modes seulement : le mode majeur et le mode harmonique mineur. Les modes anciens ont été ensuite plus ou moins oubliés pendant plusieurs siècles.
La musique modale moderne[modifier | modifier le code]
Une pratique modale moderne réapparaît progressivement au cours du XIXe siècle, avec le regain d'intérêt pour le plain-chant. Cette pratique se distingue des usages anciens, dans la mesure où elle les adapte aux principes harmoniques modernes et inclut sept modes diatoniques. Dans cette nomenclature, le mode de do dit « ionien » correspond au mode majeur classique et le mode de la à la gamme mineure naturelle (sans altération). Cette possibilité moderne d'harmoniser les modes élargit la conception classique de la tonalité fondée exclusivement sur les modes majeur et mineur, dans la mesure où elle permet de nouvelles façons de construire les enchaînements harmoniques et les cadences.
Modes diatoniques[modifier | modifier le code]


Les modes diatoniques correspondent aux sept modes construits à partir de chaque note de l'échelle diatonique. Ces modes incluent les quatre modes (forme authente) employés jadis au Moyen Âge, auxquels on a ajouté les modes de do (dit « ionien ») et de la (dit « eolien ») (forme authente) au cours de la Renaissance, puis le mode de si (dit "locrien") au cours du XIXe siècle. Ils sont souvent nommés par leur note nominale, correspondant à leur finale : mode de do, de ré, de mi, etc.
| Nom moderne | Nom courant (Glaréan, 1547) |
Nom antique présumé (Gevaert, 1875) |
Séquence d'intervalles en tons | |
|---|---|---|---|---|
| I. | Mode de do | Mode ionien | Mode lydien | 1 - 1 - 1⁄2 - 1 - 1 - 1 - 1⁄2 |
| II. | Mode de ré | Mode dorien (protus) | Mode phrygien | 1 - 1⁄2 - 1 - 1 - 1 - 1⁄2 - 1 |
| III. | Mode de mi | Mode phrygien (deuterus) | Mode dorien | 1⁄2 - 1 - 1 - 1 - 1⁄2 - 1 - 1 |
| IV. | Mode de fa | Mode lydien (tritus) | Mode hypolydien | 1 - 1 - 1 - 1⁄2 - 1 - 1 - 1⁄2 |
| V. | Mode de sol | Mode mixolydien (tetrardus) | Mode hypophrygien | 1 - 1 - 1⁄2 - 1 - 1 - 1⁄2 - 1 |
| VI. | Mode de la | Mode éolien[3] | Mode hypodorien | 1 - 1⁄2 - 1 - 1 - 1⁄2 - 1 - 1 |
| VII. | Mode de si | Mode locrien | Mode mixolydien | 1⁄2 - 1 - 1 - 1⁄2 - 1 - 1 - 1 |
Confusions historiques autour des appellations grecques[modifier | modifier le code]
On utilise fréquemment des noms grecs issus du système musical de la Grèce antique (ionien, dorien, phrygien, etc.) pour désigner chacun des sept modes diatoniques. Mais la légitimité historique de ces noms grecs dans ce contexte a été contestée au cours du XXe siècle par Jacques Chailley, qui considère que ces noms, outre le fait qu’ils sont « apocryphes » (Traité historique d'analyse harmonique, p. 81)[4] (L'Imbroglio des modes, p. 70)[5], sont trompeurs car qu’ils laissent croire que les modes utilisés dans la musique occidentale actuelle sont les mêmes que ceux utilisés dans l’Antiquité (Traité historique, p. 81)[4]. Le guide de la théorie de la musique de Claude Abromont souligne après Chailley que ces appellations grecques proviennent « d'une lecture erronée de la théorie grecque » (Guide de la théorie de la musique, p. 203)[6].
Selon Abromont, les échelles diatoniques ne correspondent pas réellement à un héritage direct de la Grèce antique, bien que les noms, eux, le soient (p. 203)[6]. En principe, la notion de mode dans la musique de la Grèce antique correspond aux différents accordages de la lyre. Le système dans la Grèce antique était tétrachordal et fonctionnait selon le principe de « modes formulaires » bien différent de la conception moderne des modes (Chailley, Traité historique, p. 81)[4] (L'Imbroglio, p. 70)[5]. On s'est rendu compte depuis que, chez Aristoxène par exemple, les noms utilisés plus tard pour les modes ne décrivaient que des échelles, ou des « espèces d'octave »[7].
Chailley a considéré que les théoriciens de la musique médiévale qui ont utilisé les noms grecs à partir du IXe siècle pour nommer leurs modes avaient mal interprété un texte de Boèce (VIe siècle), qui lui-même désignait par des noms grecs les espèces d'échelles, sans décrire leur pratique réelle[8]. L’« erreur » fut confirmée à la Renaissance par Glaréan, qui ajouta aux quatre paires de modes grégoriens (formes authente et plagale) les modes dits Ionien et Éolien et leur formes plagales (Chailley, Traité historique, p. 70)[4].
D’autre part, outre la nomenclature de Glaréan, on relève une autre nomenclature dans certains ouvrages théoriques du début du XXe siècle qui font référence à celle de Gevaert[9]. Ce dernier, qui croyait à une filiation directe entre la musique grecque et celle de l'Église latine, reprend à peu près exactement la terminologie d'Aristoxène, mais la rattache abusivement aux modes grégoriens.
Les appellations aujourd'hui régulièrement pratiquées : « ionien, dorien, phrygien, lydien, mixolydien, éolien et locrien » proviennent donc du Dodecachordon de Glaréan (1547). Pour éviter toute ambiguïté, les modes diatoniques peuvent être nommés aussi par leur « finale » (qui est la première de l'échelle dans l'appellation moderne), comme le faisait Gevaert : mode de do, de ré, de mi, de fa, de sol, de la. Le solfège classique utilise généralement cette appellation « moderne ». Cependant, comme l'observe Chailley, les noms grecs « sont aujourd'hui d'usage international » ; de plus ils sont commodes en ce qu'ils permettent une application rapide : de même qu'on dit la majeur, c'est-à-dire « ton de la en mode de do », dire la lydien signifiera « ton de la en mode de fa » (p. 81)[4]. Les jazzmen, et d'une manière générale, tous les musiciens qui utilisent la théorie et la notation jazz se servent toujours de ces appellations[10].
Musique classique moderne[modifier | modifier le code]
La musique classique moderne a été l'instigatrice de l'usage moderne des modes au cours du XIXe siècle. Les compositeurs de la fin du XIXe siècle sont venus de plus en plus à affectionner l'usage de modes, car ceux-ci connotaient pour eux des couleurs anciennes liées à l'antiquité et au Moyen Âge ainsi qu'au patrimoine populaire. Ce qu'on entend par usage moderne, c'est l'emploi d'échelles modales au sein de structures harmoniques (adaptées à la couleur et la spécificité propres de ces modes, car construites à partir même de ces modes). Les premiers compositeurs notoires à avoir tenté des essais de composition avec des échelles modales sont les élèves de Reicha : à savoir Berlioz, Liszt, Charles Gounod et César Franck. L'usage d'harmonies modales est même systématisé à l'école Niedermeyer qui vise à enseigner l'harmonisation des mélodies grégoriennes. École d'où sortira notamment Gabriel Fauré qui sera l'un des principaux compositeurs à populariser l'usage d'harmonies modales. Ensuite l'usage s'est largement étendu à la fin du XIXe siècle pour devenir totalement commun vers les années 1920.
Le fonctionnement de l'harmonie modale dans la musique classique moderne vise à répondre à la logique classique de cohérence homogène entre la mélodie et l'harmonie qui la soutient : à partir d'un mode donné, on déduit une suite d'accords adaptés aux couleurs spécifiques de ce mode. Pour faire face au fait que les mélodies grégoriennes ne contiennent pas de sensibles, on a développé une nouvelle harmonie ne s'appuyant plus sur la dynamique sensible-tonique ou sur les degrés harmoniques forts classiques. La particularité de l'usage d'une harmonie modale, étant notamment le déplacement des degrés forts et souvent la suppression de la dynamique sensible-tonique classique chère à l'harmonie tonale classique (c’est-à-dire non-moderne). Ainsi un degré fort de l'harmonie tonale comme le Ve degré devient-il un degré faible dans les modes sol, la ou encore ré. Ce Ve degré devenu secondaire et sans sensible n'a plus la force d'attraction qu'il avait dans le mode majeur ou le mineur harmonique. Parallèlement, des degrés considérés jusqu'alors comme faibles tels que le IIIe ou le IIe degré dans la musique tonale peuvent devenir des degrés forts dans la musique modale : exemple le second degré dans le mode de mi (dit « phrygien »).
Dans la pratique, il était fréquent que les compositeurs mélangent l'emploi de plusieurs modes dans un même morceau. C'était une spécialité de Fauré, qui mélangeait fréquemment modal et tonal (classique) parfois dans une même phrase par des altérations subtiles d'une note ou d'enchaînements d'accord.
Jazz[modifier | modifier le code]
Les modes constituent une ressource essentielle au niveau mélodique dans le jazz modal, où les musiciens, tout en restant sur un même accord, improvisent en exploitant différents modes.
Sur le plan théorique, le jazz modal a une conception différente de l'emploi des modes par rapport à la théorie classique de la musique tonale : en effet, au lieu d'utiliser un seul mode « matrice » et d'en dériver l'harmonie adéquate, le jazz fait l'inverse : il déduit ses modes à partir de la couleur de son harmonie, et peut utiliser un mode différent pour chaque accord plaqué. Cela s'explique notamment par le fait que le jazz modal emploie des accords « de couleur » et non des accords d'harmonie fonctionnelle (comme c'est le cas dans l'harmonie tonale classique). Sans cohésion tonale d'ensemble, il requiert par conséquent un mode différent à chaque accord pour que la mélodie s'insère correctement à chaque couleur d'accord spécifique rencontré. Chaque base d'accord constituant une sorte de tonique/finale pour un mode au niveau de la mélodie. Usage qui l'oppose totalement à la conception tonale de la musique classique.
Rock[modifier | modifier le code]
En général, le mode de la (dit « éolien ») est très fréquent dans le rock et le heavy metal. Il est à la base de progressions harmoniques typiques du genre : I-VI-VII par exemple.(exemples : Hallowed be thy Name de Iron Maiden, Breaking the Law de Judas Priest ou encore Princess of the Dawn de Accept). D'une façon générale, les musiciens de rock et de musique populaire tendent à appliquer plus ou moins les principes d'harmonie modale établis jadis par la musique classique moderne. Il y a une symbiose entre l'harmonie modale d'ensemble et une échelle mélodique employée[réf. nécessaire].
Mais certains groupes de rock inspirés par le jazz (ou du moins sa théorie) tendent à développer certaines applications modales spécifiques au jazz. Certains guitar heroes tout particulièrement qui ont souvent étudié la théorie à partir de bases jazz tendent donc au contraire à envisager l'emploi des modes « accord par accord » comme le fait le jazz[réf. nécessaire]. Cela est tout particulièrement marquant dans le fait qu'ils n'envisagent très souvent les modes que sous un aspect exclusivement mélodique[réf. nécessaire]. Au niveau mélodique, de nombreux guitaristes de rock utilisent les modes lors de leurs solos. Le mode de ré (dit « dorien ») est une composante essentielle du style de Carlos Santana. Joe Satriani et Steve Vai exploitent le mode lydien et Kirk Hammett (Metallica) est un adepte du mode phrygien[réf. nécessaire].
Modes altérés[modifier | modifier le code]
Les modes altérés sont très nombreux. On les appelle ainsi par opposition aux modes diatoniques dits modes naturels dont ils sont des variantes dans lesquelles une ou plusieurs notes sont altérées.
Il existe un total de 266 modes diatoniques distincts dans une gamme à sept degrés sur 12 demi-tons :
- Les 7 modes diatoniques naturels,
- 126 modes diatoniques à altération simple (voir ci-dessous),
- 133 modes diatoniques à altération double.
Une altération est l'ensemble des différences qui existent entre un mode altéré donné et l'un des modes diatoniques naturels. L'altération est dite simple si elle ne porte que sur deux intervalles exactement, et double si elle porte sur trois ou quatre intervalles.
L'analyse révèle que l'altération simple est associée à une amplitude maximale de deux demi-tons --l'un des deux intervalles est augmenté (resp. diminué) d'un demi-ton quand l'autre est diminué (resp. augmenté) de la même quantité-- et que l'altération double porte sur trois ou quatre intervalles pour une amplitude de 4 demi-tons.
Premier exemple d'altération simple (intervalles conjoints) :
1, 1, 1/2, 1, 1, 1, 1/2 (mode ionien)3/2, 1/2, 1/2, 1, 1, 1, 1/2 (mode altéré)
Dans ce premier exemple, l'altération simple porte sur les deux intervalles conjoints I-II et II-III : l'intervalle I-II est augmenté d'un demi-ton, passant de 1 ton à 1,5 ton, alors que l'intervalle II-III est diminué dans la même proportion, passant d'un ton à un demi-ton. De fait l'intervalle I-III est constant dans ces deux modes, et égal à deux tons.
Second exemple d'altération simple (intervalles non conjoints) :
1, 1, 1/2, 1, 1, 1, 1/2 (mode ionien)1/2, 1, 1, 1, 1, 1, 1/2 (mode altéré)
Dans ce second exemple, l'altération simple porte sur les deux intervalles non conjoints I-II et III-IV : l'intervalle I-II est diminué d'un demi-ton, passant de 1 ton à 1/2 ton, alors que l'intervalle III-IV est augmenté dans la même proportion, passant d'un demi-ton à un ton.
Exemple d'altération double :
1, 1, 1/2, 1, 1, 1, 1/2 (mode ionien)1/2, 1/2, 3/2, 1, 1, 1, 1/2 (mode altéré)
Dans ce dernier exemple, le mode altéré révèle des différences portant sur les trois intervalles conjoints I-II, II-III et III-IV : il s'agit d'une altération double. Les deux premiers intervalles, I-II et II-III, sont chacun diminués d'un demi-ton, passant de 1 ton à 1/2 ton, alors que le troisième intervalle, III-IV, est, pour compenser augmenté de deux demi-tons, passant d'un demi-ton à un ton et demi.
Notons qu'une altération double peut également porter sur quatre intervalles (e.g. le mode altéré "3/2, 1, 1/2, 1/2, 1/2, 1/2, 3/2" par rapport au mode mixolydien naturel), mais aucune altération n'implique plus de 4 intervalles.
Les modes altérés sont essentiellement construits à partir d'échelles prenant pour modèle la structure de la gamme mineure mélodique ascendante, ou encore la gamme mineure harmonique.
Modes déduits de la gamme mineure mélodique ascendante[modifier | modifier le code]
La gamme mineure mélodique a été utilisée bien avant le grand retour des modes et la théorisation moderne des modes. Bach déjà en faisait un usage très fréquent dans ses compositions contrapuntiques. Mais cette échelle n'était pas encore envisagée comme un mode dans le sens où on l'entend aujourd'hui dans la pratique tonale moderne. D'autre part, cette échelle à l'origine se distingue des autres en ce que tous ses degrés ne sont pas fixes. Son 6e et son 7e degré étant mobiles (selon que la forme est ascendante ou descendante). L'usage moderne permet d'utiliser la forme ascendante comme un mode à part entière.
Ce mode peut être interprété aussi comme une altération du mode de la (mineur naturel) au niveau de ses 6e et 7e degrés. Cette forme modale se distingue du mineur mélodique traditionnel, en ce que ses 6e et 7e degrés sont fixes et ne sont pas tenus par la règle classique de mouvement obligé entre ces deux degrés. Et il peut être utilisé aussi bien de façon ascendante que descendante. Une catégorie de modes modernes altérés se construit à partir du modèle de sa forme ascendante.
Structure[modifier | modifier le code]
| Mode | Séquence d'intervalles en tons | Nom courant, commentaire |
|---|---|---|
| I. mode mineur mélodique ascendant | 1 - 1/2 - 1 - 1 - 1 - 1 - 1/2 | Cette échelle peut être apparentée à une gamme mineure mélodique ascendante. Principale différence avec le véritable mode mineur mélodique : ses VIe et VIIe degrés sont fixes, alors qu'ils sont mobiles dans le mode mineur mélodique. |
| II. mode de ré à seconde mineure | 1/2 - 1 - 1 - 1 - 1 - 1/2 - 1 | mode dorien |
| III. mode de fa à quinte augmentée | 1 - 1 - 1 - 1 - 1/2 - 1 - 1/2 | mode lydien augmenté |
| IV. mode de fa à septième mineure, ou mode de sol à quarte augmentée |
1 - 1 - 1 - 1/2 - 1 - 1/2 - 1 | mode de Bartók, mode lydien |
| V. mode de sol à sixte altérée | 1 - 1 - 1/2 - 1 - 1/2 - 1 - 1 | mixolydien |
| VI. mode de la à quinte diminuée, ou mode de si à seconde majeure |
1 - 1/2 - 1 - 1/2 - 1 - 1 - 1 | éolien |
| VII. mode de si à quarte diminuée | 1/2 - 1 - 1/2 - 1 - 1 - 1 - 1 | mode altéré, super locrien, ou locrien |
Utilisations[modifier | modifier le code]
La gamme mineure mélodique était utilisée bien avant l'usage des modes. Mais l'usage moderne de la forme ascendante en tant que mode à part entière a été pratiqué au début du XXe siècle notamment par Fauré. Le mode majeur-mixte (dit mixolydien ![]() 6) en classique a aussi été utilisé, notamment par Gabriel Fauré (exemple « Ce sera par un clair jour d'été » - La bonne chanson) et on en trouve même des exemples précoces dans l'histoire de la musique chez Schubert. Debussy utilise le mode acoustique (dit « lydien dominant ») notamment dans la Mer. Mais c'est certainement Béla Bartók qui en a fait l'usage le plus notoire. D'où le fait qu'on lui ait souvent donné le nom de mode de Bartók.
6) en classique a aussi été utilisé, notamment par Gabriel Fauré (exemple « Ce sera par un clair jour d'été » - La bonne chanson) et on en trouve même des exemples précoces dans l'histoire de la musique chez Schubert. Debussy utilise le mode acoustique (dit « lydien dominant ») notamment dans la Mer. Mais c'est certainement Béla Bartók qui en a fait l'usage le plus notoire. D'où le fait qu'on lui ait souvent donné le nom de mode de Bartók.
Dans le jazz, cette forme de l'échelle et les modes déduits de celle-ci sont couramment utilisés à partir de la fin des années 1950[13]. Hormis dans les styles dit progressifs, ces modes sont rarement utilisés dans le rock et le heavy metal.
Modes déduits de la gamme mineure harmonique[modifier | modifier le code]
La gamme harmonique mineure a été utilisée bien avant le grand retour des modes et la théorisation moderne des modes. À l'époque classique où seuls deux modes étaient employés (majeur et mineur), cette gamme constituait le pendant mineur du mode majeur. Le mode mineur naturel (ou mode de la, dit éolien) étant totalement ignoré à cette époque, c'est la gamme harmonique mineure qui était principalement utilisée dans toute la production classique ancienne. Même si parfois on avait recours à la gamme mineure mélodique dans les compositions contrapuntiques. Cette gamme était privilégiée à l'époque car elle permettait de transposer au mode mineur la relation sensible-tonique du mode majeur essentielle aux yeux des compositeurs classiques. C'est pourquoi son emploi au sein d'une structure harmonique déduite de celle-ci tend à connoter souvent une couleur classique traditionnelle.
Depuis, beaucoup de théoriciens du jazz et du rock tendent à envisager indifféremment la gamme harmonique mineure comme un mode parmi d'autres plutôt que comme le mode mineur par excellence comme le font encore les théoriciens du classique. Mais l'approche moderne des modes, tout particulièrement dans le jazz, a exploité la disposition d'échelle spécifique de la gamme harmonique mineure pour en déduire de nouveaux modes à partir d'autres finales sur l'échelle. Ce qui donne 6 autres nouveaux modes. Ces nouveaux modes n'ont pas de noms officiels mis à part l'emploi de termes grecs dérivés.
| Séquence d'intervalles en tons | Nom courant, commentaire | |
|---|---|---|
| I. | 1 - 1/2 - 1 - 1 - 1/2 - 3/2 - 1/2 | mode mineur harmonique (identique à une gamme mineure harmonique) |
| II. | 1/2 - 1 - 1 - 1/2 - 3/2 - 1/2 - 1 | mode locrien naturel |
| III. | 1 - 1 - 1/2 - 3/2 - 1/2 - 1 - 1/2 | mode ionien augmenté |
| IV. | 1 - 1/2 - 3/2 - 1/2 - 1 - 1/2 - 1 | mode dorien |
| V. | 1/2 - 3/2 - 1/2 - 1 - 1/2 - 1 - 1 | mode mixolydien |
| VI. | 3/2 - 1/2 - 1 - 1/2 - 1 - 1 - 1/2 | mode lydien |
| VII. | 1/2 - 1 - 1/2 - 1 - 1 - 1/2 - 3/2 | mode diminué diatonique |
On tend parfois à rapprocher le mode dorien ![]() 4 (noté IV) de la gamme tzigane à cause de la place de la seconde augmentée qui se trouve sur les mêmes degrés que la gamme tzigane. Mais la vraie gamme tzigane s'en distingue dans le fait que celle-ci est caractérisée par une double seconde augmentée.
4 (noté IV) de la gamme tzigane à cause de la place de la seconde augmentée qui se trouve sur les mêmes degrés que la gamme tzigane. Mais la vraie gamme tzigane s'en distingue dans le fait que celle-ci est caractérisée par une double seconde augmentée.
Même si le mode phrygien ![]() 3 (noté V) présente les caractéristiques du mode andalou, il s'en distingue en ce que ses degrés sont fixes, tandis que le mode andalou tel qu'il est utilisé dans la musique traditionnelle se caractérise par la mobilité de ses 3e et 7e degrés. Elle est aussi souvent confondue à tort avec la gamme orientale du fait de la place de sa seconde augmentée caractéristique. Mais elle s'en distingue dans le fait que la vraie gamme orientale est constituée de deux secondes augmentées et une sensible ascendante au 7e degré. Contrairement à ce mode dont le 7e degré est une sous-tonique à distance de seconde majeure de la tonique.
3 (noté V) présente les caractéristiques du mode andalou, il s'en distingue en ce que ses degrés sont fixes, tandis que le mode andalou tel qu'il est utilisé dans la musique traditionnelle se caractérise par la mobilité de ses 3e et 7e degrés. Elle est aussi souvent confondue à tort avec la gamme orientale du fait de la place de sa seconde augmentée caractéristique. Mais elle s'en distingue dans le fait que la vraie gamme orientale est constituée de deux secondes augmentées et une sensible ascendante au 7e degré. Contrairement à ce mode dont le 7e degré est une sous-tonique à distance de seconde majeure de la tonique.
Utilisations[modifier | modifier le code]
La gamme harmonique mineure est la gamme mineure par excellence du classique. Elle fut presque exclusivement utilisée dans la musique classique du XVIe siècle- au XIXe siècle, jusqu'au retour de l'emploi d'autres modes à la fin du XIXe siècle. Il était évité par contre de faire entendre sa seconde augmentée. En cas d'enchaînement des trois derniers degrés de la gamme, on préférait alors l'emploi du mineur mélodique ascendant ou descendant en fonction de la direction du mouvement mélodique. En revanche, les modes dérivées de son modèle d'échelle sont peu utilisés dans la production moderne classique. Il existe un exemple célèbre de l'usage du dorien ![]() 4 dans la première Gnossienne de Satie.
4 dans la première Gnossienne de Satie.
La gamme harmonique mineure est particulièrement affectionnée dans le rock progressif et chez les guitaristes de hard rock influencés par la musique classique tels que Yngwie Malmsteen. Car son emploi connote une couleur typiquement classique. En revanche les modes dérivés sont peu utilisés, excepté le mode dit phrygien ![]() 3 qui est très largement utilisé dans la musique populaire à la place de la gamme orientale. La musique populaire assimile très souvent l'un à l'autre à cause de leurs sonorités très proches, elle a souvent tendance à utiliser le phrygien
3 qui est très largement utilisé dans la musique populaire à la place de la gamme orientale. La musique populaire assimile très souvent l'un à l'autre à cause de leurs sonorités très proches, elle a souvent tendance à utiliser le phrygien ![]() 3 pour connoter des ambiances orientales ou antiques : exemple Krakatau de Yngwie Malmsteen ou encore Eleven Blue Egyptian de Jason Becker. D'autres groupes de rock et de metal l'utilisent également dans d'autres contextes, Offspring (Come out and Play) ou encore Accept (Metal Heart (solo), Lay it Down on Me (intro) notamment), Lacuna Coil (Heir of a Dying Day). La gamme et ses modes dérivés sont parfois utilisés dans le jazz, mais la gamme mineure mélodique lui est souvent préférée[14]. Django Reinhardt, initiateur du style Jazz manouche l'utilisait abondamment[réf. nécessaire].
3 pour connoter des ambiances orientales ou antiques : exemple Krakatau de Yngwie Malmsteen ou encore Eleven Blue Egyptian de Jason Becker. D'autres groupes de rock et de metal l'utilisent également dans d'autres contextes, Offspring (Come out and Play) ou encore Accept (Metal Heart (solo), Lay it Down on Me (intro) notamment), Lacuna Coil (Heir of a Dying Day). La gamme et ses modes dérivés sont parfois utilisés dans le jazz, mais la gamme mineure mélodique lui est souvent préférée[14]. Django Reinhardt, initiateur du style Jazz manouche l'utilisait abondamment[réf. nécessaire].
Modes exotiques[modifier | modifier le code]
Outre les modes constitués à partir du modèle de gammes traditionnelles de la musique occidentale, il existe de nombreuses autres échelles d'où peuvent être déduits des modes. Notamment les modes dits « exotiques » dans la théorie musicale occidentale. De nombreuses traditions musicales de différentes régions du monde s'appuient en effet sur des échelles originellement inconnues du langage occidental classique. Il va de soi que, pour ces cultures, ces échelles n'ont aucunement un caractère « exotique ». Mais elles ont fini par susciter l'intérêt des musiciens occidentaux qui les ont adaptées au langage tonal, pour créer de nouvelles couleurs ou pour les utiliser à des fins d'évocation exotique dans leur musique. Les premières gammes exotiques à être adaptées dans le langage tonal classique furent l'échelle à double seconde augmentée et les gammes pentatoniques. La première fut utilisée dès les années 1840 par Liszt et Glinka. Quant à la gamme pentatonique, on en relève un exemple dès 1828 chez Chopin vraisemblablement influencé par le folklore polonais dans la krakowiak. Mais on en trouvera par la suite de nombreux exemples précoces chez Liszt.
Échelle à double seconde augmentée[modifier | modifier le code]
Cette échelle est la plus employée en matière d'exotisme. En effet, elle est présente dans différentes cultures (musique arabe, indienne, russe, hongroise, roumaine, espagnole) selon les formes modales qu'elle prend. C'est pourquoi les musiciens en quête d'effet exotique ont tendance à la considérer comme la « gamme exotique » par excellence. Le terme « échelle à seconde augmentée » vient du fait que cette échelle se caractérise par un intervalle de seconde augmentée dans chacun des tétracordes qui constitue l'octave.
Les deux formes principales de cette échelle sont la gamme dite « orientale » et la gamme dite « tzigane », les deux formes se distinguant dans le fait qu'elles placent différemment les intervalles de seconde augmentée.
Gamme orientale[modifier | modifier le code]
Les musiques orientales dans leur ensemble offrent une immense variété de modes, généralement inconnus dans la musique occidentale. Mais c'est surtout cette gamme qu'on associe le plus souvent à l'idée d'Orient dans la musique occidentale. En vérité, la gamme appelée « orientale » n'est qu'un mode stylisé adapté à la musique occidentale. Car les modes de la vraie musique orientale se structurent sur des échelles contenant des intervalles de trois-quarts de tons, et non des "quarts de tons" comme on peut le lire quelquefois. Exemple : la tierce mineure ré-fa, monnayée en occident en [ton+demi-ton] (ré-mi-fa) ou en [demi-ton+ton] (ré-mib-fa) est monnayée dans un contexte « oriental » en [3/4 ton + 3/4 ton] (ré-mibb-fa), ce qui donne 1 ton et demi en tout, mais pas de « quarts de tons », donc.
Toujours est-il que c'est cette échelle (popularisée par Saint-Saëns et Liszt) qui fut le plus largement employée dans la musique classique et la musique de film pour évoquer l'Orient. Cette gamme est une des formes les plus utilisées de l'échelle à double-seconde augmentée. Elle se caractérise par la symétrie de ses deux tétracordes et par ses deux secondes augmentées au milieu de ses deux tétracordes (ré![]() -mi et la
-mi et la![]() -si).
-si).

Intervalles : 1/2 ton - 3/2 tons - 1/2 ton - 1 ton - 1/2 ton - 3/2 tons - 1/2 ton
C'est en effet l'intervalle de seconde augmentée qui confère à cette sonorité ses accents pseudo-orientaux. Et c'est à cause de cet intervalle qu'elle est souvent confondue avec le mode dit phrygien ![]() 3. La différence étant que ce dernier n'est constitué que d'une seule seconde augmentée :
3. La différence étant que ce dernier n'est constitué que d'une seule seconde augmentée :

La gamme orientale a en outre la particularité d'avoir deux sensibles. Une sensible traditionnelle ascendante (si→do) et une sensible harmonico-modale descendante (ré![]() →do).
→do).
À cause de sa symétrie, le tétracorde supérieur de la gamme peut constituer le tétracorde d'une même gamme transposée à la dominante :


Mais ce mode a pu être aussi utilisé pour évoquer l'Inde. Cette gamme correspondant aussi à un des modes de l'Inde du nord : Le Bhairava qu'Albert Roussel utilise notamment dans Padmâvatî. Bizet utilisait aussi cette gamme dans un esprit hispanisant dans son opéra Carmen : le fameux thème du destin.
Gamme tzigane[modifier | modifier le code]
En comparaison, la gamme orientale peut être vue comme le plagal d'un autre mode : la gamme tzigane. C'est pourquoi les deux sont parfois confondues.
Exemple sur do :

Intervalles : 1 ton - 1/2 ton - 3/2 tons - 1/2 ton - 1/2 ton - 3/2 tons - 1/2 ton
Franz Liszt l'emploie à profusion, notamment dans sa Rhapsodie Hongroise no 13 en la mineur :
Mode balkanique[modifier | modifier le code]
En musique balkanique, le mode le plus utilisé, connu sous de nombreux noms, est le mode de mi, mais avec une 7e majeure. L'espacement équivaut à ce schéma :
1/2 ton - 1 ton - 1ton - 1 ton - 1/2 ton - 3/2 tons - 1/2 ton
Par exemple :
- dans le ton de mi :
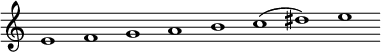
- dans le ton de do :

Mode andalou[modifier | modifier le code]
Exemple sur do :

Intervalles : 1/2 ton - 3/2 tons - 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1 ton
Proche du mode de mi, dans la musique traditionnelle, le mode andalou se caractérise par la mobilité de son 3e degré pour éviter la seconde augmentée, mais jouant sur l'expression de son renversement la septième diminuée particulièrement dans un mouvement mélodique descendant. Plus rarement le 7e degré peut passer de sous-tonique (à distance de seconde majeure de la tonique), à sensible (à un demi-ton). On retrouve par exemple le mode andalou dans le ballet L'Amour sorcier de Manuel de Falla ou dans le deuxième thème du Boléro de Maurice Ravel. Il est (enharmoniquement) équivalent au mode phrygien ![]() 3 (également appelé phrygien dominant ou phrygien majeur[réf. souhaitée]) décrit plus haut, constituant le 5e mode de la gamme mineure harmonique.
3 (également appelé phrygien dominant ou phrygien majeur[réf. souhaitée]) décrit plus haut, constituant le 5e mode de la gamme mineure harmonique.
Modes indiens[modifier | modifier le code]
Melakarta[modifier | modifier le code]
Vāchaspati[modifier | modifier le code]
Le raga Vāchaspati en musique carnatique indienne utilise la même échelle qu'un mode mixolydien dont le quatrième degré serait augmenté.
Exemple sur do :
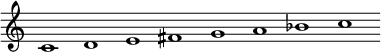
Intervalles: 1 ton - 1 ton - 1 ton - 1/2 ton - 1 ton - 1/2 ton - 1 ton
Ce mode est également connu sous le nom de « gamme Bartók », « lydien dominant », « lydien ![]() 7 », « mode acoustique », « mixolydien
7 », « mode acoustique », « mixolydien ![]() 4 », « IVe mode de la gamme mineure mélodique ».
4 », « IVe mode de la gamme mineure mélodique ».
Échelles défectives[modifier | modifier le code]
On appelle échelle -ou mode- défectif (ive) un mode qui contient moins (ex. : mode pentatonique) de sept notes à l'octave.
Gammes pentatoniques[modifier | modifier le code]
La gamme pentatonique est couramment utilisée par les guitaristes rock. Elle est constituée comme son nom l'indique de 5 notes, ces notes étant obtenues par une progression dans le cycle des quintes, comme :
do - sol - ré - la - mi
Ce qui donne après triage :
do ré mi sol la do
Les relatifs obtenus par renversement (rotation) :
sol la do ré mi sol
ré mi sol la do ré
la do ré mi sol la
mi sol la do ré mi
Le mode basé sur la est proche du mode blues :
Ces modes sont caractérisés par des intervalles de secondes majeures ou de tierces mineures :
Intervalles : 1 - 1 - 3/2 - 1 - 3/2
Exemple en mi : do ré mi sol la do
Gammes tétraphoniques[modifier | modifier le code]
Autre type d'échelle défective parfois employée, la gamme tétraphonique, c’est-à-dire une gamme à quatre sons. Il en existe plusieurs. À l'écoute, elles ne sont pas sans rappeler la couleur des gammes pentatoniques. Elles ont été souvent employées dans la musique classique pour évoquer des éléments primitifs ou naturalistes
Cette gamme notamment :
a été utilisée par Claude Debussy dans De l'aube à midi sur la mer dans La Mer
et par Igor Stravinsky dans l'introduction de l’Adoration de la terre du Sacre du Printemps
En théorie elle peut aussi être constituée de tierces mineures. Par exemple :
Intervalles : 3/2 tons - 3/2 tons - 3/2 tons - 3/2 tons
Ce qui l'apparente directement à un arpège d'accord de septième diminuée. Accord fréquemment utilisé dans des contextes tonaux et modaux. Mais dans ces cas il ne s'agit plus précisément de gammes tétraphoniques. On ne peut donc pas envisager l'emploi de ces accords comme ceux d'une gamme tétraphonique dans ces contextes.
Gammes hexaphoniques[modifier | modifier le code]
Les gammes hexaphoniques, comme leur nom l'indique, sont constituées de six degrés. La gamme hexaphonique la plus célèbre étant la gamme par ton abordée au paragraphe suivant. On peut trouver dans le blues ou dans la musique contemporaine des gammes hexaphoniques à 6 degrés inégaux.
Exemple : do mi![]() fa fa
fa fa![]() la si do
la si do
Intervalles : 3/2 tons - 1 ton - 1/2 ton - 3/2 ton - 1 ton - 1/2 ton
Modes artificiels à transposition limitée[modifier | modifier le code]
Gamme par ton[modifier | modifier le code]
La gamme par ton est une gamme ou tous les intervalles sont de 1 ton.
Exemple sur do :

Indépendamment de toute enharmonie, il n'existe que deux transpositions de la gamme par tons.
La première part de do et est décrite ci-dessus. La seconde part de do![]() et donne, en prenant la même convention (tous les tons diatoniques représentés à l'exception du degré VII, enharmonies représentées entre parenthèses pour simplifier la lecture) :
et donne, en prenant la même convention (tous les tons diatoniques représentés à l'exception du degré VII, enharmonies représentées entre parenthèses pour simplifier la lecture) :

Toute transposition ramène à l'une de ces deux possibilités, par enharmonie ou non. Par exemple, à partir de mi, on a un équivalent de la gamme par tons en do :

Mode diminué (ou mode ton/demi-ton, ou mode Bertha)[modifier | modifier le code]
Le mode diminué est très utilisé en jazz : il correspond au septième mode du mineur mélodique (auquel on ajoute un degré entre le V et le VII, le VI étant remplacé par les notes situées 1/2 ton au-dessus et en dessous). On peut utiliser ce mode en général sur un accord diminué (quinte et septième diminuées). Les intervalles sont 1 ton - 1/2 ton mais on trouve aussi le diminué inverse qui est 1/2 ton - 1 ton. On peut utiliser ce mode en général sur un accord de dominante avec 9e mineure et 13e majeure (V7 13b9).
Exemples :

Intervalles : 1 ton - 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1/2 ton
Intervalles par rapport à la note fondamentale : 1 9 m3 11 ![]() 5
5 ![]() 6 7dim maj7
6 7dim maj7
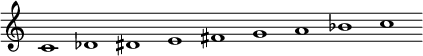
Intervalles : 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1/2 ton - 1 ton
Intervalles par rapport à la note fondamentale : 1 ![]() 9
9 ![]() 9 3
9 3 ![]() 11 5 13 b7
11 5 13 b7
Ces modes possèdent 8 degrés, au lieu des 7 qu'on trouve dans les modes les plus courants. Ils génèrent des tensions supplémentaires très appréciées dans le jazz. Chaque catégorie ne possède que trois gammes car il s'agit d'un schéma répétitif. Toute transposition ramène à l'une d'entre elles, par enharmonie ou non.



Dans la théorie d'Olivier Messiaen, ce mode correspond au deuxième des sept modes à transposition limitée.
Modes microtonaux[modifier | modifier le code]
L'écriture à partir de micro-intervalles est traditionnellement employée dans le monde arabe et en Inde. Dans la musique arabe, l'intervalle est assez souvent le trois quarts de ton, mais des chercheurs américains analysant la musique arabe au moyen d'instruments de mesure ont conclu qu'on rencontre également des intervalles de 2/3 de ton. Les instrumentistes utilisent généralement à l'avenant les possibilités d'un instrument dont la gamme n'est pas « prédéfinie » par le luthier selon un accordage strict comme c'est le cas pour beaucoup d'instruments occidentaux. Tel est le cas de la célèbre mezoued tunisienne. Il est possible que ce soit également le cas du « neï » (=flûte arabe). Dans l'Occident, il existe une foule d'instruments pouvant créer des microtons, c'est le cas du violon (employé par les musiciens du monde arabe), et plus généralement des instruments anciens à cordes (violoncelles, contrebasse…), mais aussi des instruments électroniques comme les Ondes Martenot ou le Thérémine, ces derniers étant a priori inconnus du monde arabe. La trompette arabe mise au point à Paris par Nassim Maalouf permet de produire tous les intervalles nécessaires aux maqams arabes par l'introduction d'un quatrième piston abaissant d'un quart de ton les notes produites par les trois premiers[réf. nécessaire].
Dans la musique moderne électrique occidentale, on peut citer quelques compositeurs avant-gardistes, tel Chick Corea (époque Miles Davis) qui avait « détonné » son piano électrique (toutefois, seulement quelques notes, et à notre connaissance, sans emploi réellement modal). Karl Jenkins, dans l'album Soft Machine 7 utilisait des enregistrements d'instruments à anche (probablement la clarinette basse) en le superposant à une mélodie d'inspiration rileyienne, ce qui n'est pas sans créer une certaine confusion chez l'auditeur. Le passage en question est signé Ratletge/Jenkins.
Notes et références[modifier | modifier le code]
- Harold Powers e.a., « Mode », The New Grove Online, présentation en ligne DOI 10.1093/gmo/9781561592630.article.43718(accès réservé)
- Marc Honegger, Histoire de la Musique : la musique occidentale, du Moyen âge à nos jours, Paris, Bordas, , 630 p. (ISBN 2-04-015303-9), p. 32
- « Éolien » est l'orthographie telle qu'elle est employée par des musicologues comme Claude Abromont, Guide de la théorie de la musique, Fayard, 2001, p. 204, Jacques Chailley, Traité historique d'analyse harmonique, Alphonse Leduc, 1981,p. 81 ou encore Serge Gut,"Transformations et résistances d'un corpus de mélodies folkloriques françaises sous l'influence de la tonalité classique" in Manfred Kelkel(éd.)Musicologie au fil des siècles, Presses de l'université Paris-Sorbonne, 1998, p. 125, 126 et passim. D'autres auteurs utilisent la forme « aéolien » [réf. nécessaire].
- Chailley, Jacques, Traité historique d'analyse harmonique, Alphonse Leduc,
- Chailley, Jacques, L'imbroglio des modes, Leduc,
- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. (ISBN 978-2-213-60977-5)
- Thomas J. Mathiesen, « Greek music theory », The Cambridge History of Western Music Theory, Cambridge University Press, 2002, p. 124-125.
- Boèce, De institutione musica, G. Friedlein ed., Leipzig, 1867, p. 342 sq.
- François-Auguste Gevaert, Traité d'Harmonie, Paris, Bruxelles, Lemoine, 1905, p. 14-19 et 22.
- « Modes jazz », sur Wikiversité,
- Raganidhi par P. Subba Rao, 1964, The Music Academy of Madras
- D'après la théoricienne Françoise Gervais[source insuffisante].
- Levine, op. cit., chapitre III section 2.
- Levine, op. cit., chapitre XXIII, section 2.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Liste des gammes et modes
- Modulation
- Modes de la musique tonale
- Musique modale
Bibliographie[modifier | modifier le code]
- Jacques Chailley, L'Imbroglio des modes, Paris, Alphonse Leduc, , 4e éd. (1re éd. 1960), 92 p.
- Jacques Chailley, Traité historique d'analyse harmonique, Paris, Alphonse Leduc, (1re éd. 1951), 158 p. (ISBN 2-85689-037-7)
- Jef Gilson, L'harmonie du Jazz, Paris, Association PALM (Association pour l'accès au langage musical), (1re éd. 1978), 40 p.
- Mark Levine, Le livre de la théorie du jazz, Advance Music, , 466 p. (ISBN 978-3-89221-054-2)
- Jacques Siron, La partition intérieure : jazz, musiques improvisées, Outre Mesure, , 765 p. (ISBN 2-907891-03-0)
- Philippe Gouttenoire et Jean-Philippe Guye, Vocabulaire pratique d'analyse musicale, DELATOUR FRANCE, , 128 p. (ISBN 978-2-7521-0020-7)
- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. [détail des éditions] (ISBN 978-2-213-60977-5)
Liens externes[modifier | modifier le code]
- Les sept modes de la gamme majeure avec des exemples audio sur sweepyto.net
- (fr) Liste des gammes et de leurs modes respectifs
- Modes musicaux, les 2047 modes possibles avec un système à 12 notes par octave sur jeanpierrepoulin.com
- (en) Liste et « notes » sur de nombreuses gammes synthétiques, exotiques… (par Mattias IA Eklundh), sur Freak Guitar


