Classement Elo

Pour les articles homonymes, voir Elo.

Joueurs d’échecs.

Le classement Elo est un système d’évaluation du niveau de capacités relatif d’un joueur d’échecs ou de jeu de go, ou d’autres jeux à deux joueurs. Plus généralement, il peut servir à comparer deux joueurs d’une partie, et est utilisé par de nombreux jeux en ligne.

Elo se trouve parfois écrit par erreur en haut de casse ELO. Or, il ne s’agit pas d’un acronyme. Il doit son nom à Arpad Elo (1903-1992), un professeur de physique et excellent joueur d’échecs américain d’origine hongroise qui l’a mis au point.

Principe

Plus le classement Elo est élevé, plus le joueur est estimé être performant. Si un joueur obtient des performances supérieures à son niveau estimé, il est censé gagner des points Elo, et en perdre s'il réalise des contre-performances. L'ordre chronologique des classements compte: pour un joueur qui a un classement Elo initial de $R_t$ (R pour rating) à l'issue de la période t, $R_(t+1)$ n'est pas une fonction linéaire de $R_t$. Par exemple, s'il perd 15 points Elo lors de la période t+1, sa performance attendue pour la période suivante t+2 est elle-même abaissée de 15 points, ce qui fait qu'avec une performance en t+2 conforme à son niveau initial de $R_t$, il pourrait gagner lors de cette période (par exemple) 20 points Elo.

Historique

La Fédération américaine des échecs (USCF), a utilisé le système d’Arpad Elo dès 1960. Il fut ensuite adopté par la Fédération internationale des échecs (FIDE) en 1970. Arpad Elo a décrit son travail dans les détails dans son livre The Rating of Chessplayers, Past and Present, publié en 1978.

Arpad Elo avait étudié la force des joueurs en se basant sur leurs résultats, et en avait déduit que leur force pouvait se mesurer par un classement en points distribué selon une loi normale de répartition.

Des tests statistiques ultérieurs ont montré que la force échiquéenne n’est pas tout à fait distribuée selon une loi normale. Aussi, l’USCF et la FIDE ont fait évoluer la formule de calcul vers une loi logistique. Cependant par respect pour la contribution du professeur Elo, le nom du classement international continue d’être appelé le « classement Elo ».

Théorie mathématique

Le classement Elo est fondé sur une mesure de la force relative des joueurs.

La force relative entre deux joueurs peut être déterminée facilement si ceux-ci ont disputé entre eux un nombre significatif de parties. Le résultat statistique obtenu détermine une probabilité de gain pour les parties à venir entre ces deux joueurs. L’idée du classement Elo est de convertir à l’aide d’une fonction la probabilité de gain d’un joueur contre un autre en une mesure qui exprime l'écart de niveau entre les deux joueurs. Grâce à cette mesure, il sera possible de classer ensemble des joueurs qui ne se sont pas rencontrés directement.

Un exemple de fonction est le suivant pour un cas où l'on considère qu'un joueur n'a statistiquement aucune chance de remporter la partie qui l'oppose à un joueur mieux classé de 700 points (ou plus) que lui. La table de conversion indique ici l'écart E(p) en nombre de points entre un joueur A et un joueur C à partir de la probabilité de gain de A contre C dénommée p = P (A/C):

P (A/C) E(p)	P (A/C) E(p)	P (A/C) E(p)	P (A/C) E(p)	P (A/C) E(p)
99% 677	79% 230	59% 65	39% -80	19% -251
98% 589	78% 220	58% 57	38% -87	18% -262
97% 538	77% 211	57% 50	37% -95	17% -273
96% 501	76% 202	56% 43	36% -102	16% -284
95% 470	75% 193	55% 36	35% -110	15% -296
94% 444	74% 184	54% 29	34% -117	14% -309
93% 422	73% 175	53% 21	33% -125	13% -322
92% 401	72% 166	52% 14	32% -133	12% -336
91% 383	71% 158	51% 7	31% -141	11% -351
90% 366	70% 149	50% 0	30% -149	10% -366
89% 351	69% 141	49% -7	29% -158	9% -383
88% 336	68% 133	48% -14	28% -166	8% -401
87% 322	67% 125	47% -21	27% -175	7% -422
86% 309	66% 117	46% -29	26% -184	6% -444
85% 296	65% 110	45% -36	25% -193	5% -470
84% 284	64% 102	44% -43	24% -202	4% -501
83% 273	63% 95	43% -50	23% -211	3% -538
82% 262	62% 87	42% -57	22% -220	2% -589
81% 251	61% 80	41% -65	21% -230	1% -677
80% 240	60% 72	40% -72	20% -240

En pratique, la règle des 350 points d'écart pour la non-prise en compte des résultats "logiques" a été remplacée par la règle des 400 points, ce qui fait que l'espérance de performance pour le joueur A contre le joueur C comprendra l'expression ${\frac{E(p)}{400}}$ et non ${\frac{E(p)}{350}}$.

Pour exprimer l'écart de niveau entre plus de deux joueurs, le problème se pose dans les termes suivants : connaissant la probabilité de gain d’un joueur A contre un joueur B ainsi que celle de B contre un joueur C, quelle est la probabilité de gain de A contre C ?

$q = P (A/B) \;$ la probabilité de gain de A contre B.

$r = P (B/C) \;$ la probabilité de gain de B contre C.

$p = P (A/C) \;$ selon la Loi logistique la probabilité théorique de gain de A contre C est telle que :

$\frac{p}{1-p}=\frac{q}{1-q}\times\frac{r}{1-r}$

Le rapport entre la probabilité et son complément exprime la force relative f entre deux joueurs.

La force de A contre C est donc égale au produit des forces intermédiaires, celle de A contre B par celle de B contre C :

$f (p) = f (q) \times f (r)$ avec $f (p) = \frac{p}{1 - p}$ et de la force peut se déduire la probabilité : $p = \frac {f ( p )}{ 1 + f ( p )}$

Exemple :

Avec q = 60 %, f(q) = 0,60 / 0,40 = 1,5, A est une fois et demi plus fort que B.

Avec r = 66 %, f(r) = 0,66 / 0,33 = 2, B est deux fois plus fort que C.

f (p) = f (q) x f (r) = 1,5 x 2 = 3, A est trois fois plus fort que C.

Avec f (p) = 3 la probabilité de gain de A contre C est p = 3 / 4 soit 75 %.

La force f est une mesure, mais pour obtenir un classement il faut une fonction D(p) telle que : D(p) = D(q) + D(r) de façon à ce que l’écart mesuré entre A et C soit égal à la somme des écarts mesurés entre A et B d’une part et B et C d’autre part, ce qui n’est pas le cas avec le produit des forces.

Posons $\ D ( p ) = t [ f ( p ) ] \;$ où t est une fonction à définir.

$\ D ( p ) = \ D ( q ) + \ D ( r ) \Leftrightarrow t [ f (p) ] = t [ f (q) ] + t [ f (r) ] \;$

Nous avons donc :

$f ( p ) = f ( q ) \times f ( r ) \Rightarrow t [ f (q) \times f (r) ] = t [ f (q) ] + t [ f (r) ]$

Cette transformation par t d’un produit en somme est la définition de la fonction logarithme.

Le logarithme décimal noté log est choisi pour t et pour étendre la plage de valeurs, le facteur multiplicatif fixé à 400 est introduit.

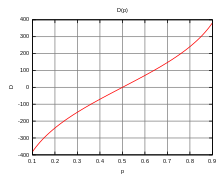
D'où la formule Elo :

$\ D ( p ) = 400 \times \log (\frac {p}{1 - p})$

D(p)

Exemple :

Avec q = 0,60 et r = 0,66, les forces sont f(q) = 1,5, f(r) = 2 et f(p) = 3.

D(q) = 400 x log (1,5) = 400 x 0,176 = 70,4

D(r) = 400 x log (2) = 400 x 0,301 = 120,4

D(p) = 400 x log (3) = 400 x 0,477 = 190,8

Nous avons bien D(p) = 70,4 + 120,4 = 190,8

p(D)

La fonction réciproque p(D) donne la probabilité de gain en fonction de la différence Elo D :

$p (D) = \frac{1}{1 + 10^{\frac{-D}{400}}}$

Mode de calcul

Application pratique

Aux échecs, la fonction p (d) est utilisée pour calculer le nouvel Elo E_n+1 en fonction de l'ancien E_n :

$E_{n+1}= E_n + K \times (W - p(D))$

W est le résultat de la partie : 1 pour une victoire, 0,5 pour un nul et 0 pour une défaite.

p(D) représente le résultat attendu de la part du joueur en fonction de la différence D avec son adversaire.

La différence W – p(D) traduit l’écart entre résultat effectif et résultat attendu. Un résultat attendu p(D) égal au résultat réel W ne changera donc pas le Elo.

K est un coefficient de développement : 30 pour les 30 premières parties, 15 tant que le joueur est en dessous de 2400 points Elo et définitivement 10 ensuite.

Exemple

Un joueur classé 1800 joue contre un joueur classé 2005. $D=1800-2005=-205$. Il a une probabilité de gain de : $p(D) = 0,235 \;$

En faisant match nul (W = 0,5), avec K= 15, cela lui donne un nouveau classement :

$E_{n+1} = 1800 + 15 \times (0,5 - 0,235) = 1800 + 4 = 1804$

Le joueur classé 2005 perd de son coté 4 points

En pratique la FIDE limite ses calculs en plafonnant D à 400 points, c’est-à-dire que s’il y a plus de 400 points d’écart, donc plus de 91 % de chances de gain théoriques, la différence est ramenée à 400 points.

Le coefficient K

Nombre de GMI par tranche de 10 points Elo (juillet 2009).

Du facteur K dépend la volatilité du classement, plus K est élevé et plus les variations du classement seront amplifiées. Cela pour permettre aux nouveaux joueurs entrants dans le classement de progresser rapidement vers leur niveau réel. Les joueurs anciens dans le classement ont un facteur K moins élevé et les joueurs qui ont atteint un Elo supérieur à 2400 ont leur facteur K au minimum.

Historiquement à l’initialisation du processus en 1970, il fut décidé que tous les grands maîtres internationaux du monde avaient un classement de 2 500 points Elo. C’est à partir de cette base de joueurs initiale que le classement s’est progressivement calculé pour tous les autres joueurs.

La moyenne du classement Elo des Grand Maîtres Internationaux n'a que très peu varié depuis 1970 et s'établit toujours à 20 points près autour de 2500 points Elo. Ce rappel invalide les « théories de l'inflation » du classement Elo. Il y a par contre plus de joueurs actifs, donc plus de Grand Maîtres et donc comme dans toute Loi de distribution plus de joueurs se situant aux extrêmes. Il est donc normal que, avec une moyenne générale stable, la moyenne du classement des seuls 10 meilleurs joueurs du monde augmente en relation avec le nombre total de joueurs actifs, tout comme la moyenne des 10 Grands Maîtres les moins biens classés baissera de la même façon.

Calcul du classement FIDE

Premier classement d'un joueur

Extrait de la table FIDE

$p$	$d(p)$
1.00	+ 800
0.99	+ 677
0.9	+ 366
0.8	+ 240
0.7	+ 149
0.6	+ 72
0.5	0
0.4	− 72
0.3	− 149
0.2	− 240
0.1	− 366
0.01	− 677
0.00	− 800

On veut déterminer le premier classement (classement initial), R_n, du joueur.

On calcule d'abord le classement R_u (R pour rating, u pour unknown, inconnu) du joueur dans une compétition où il rencontre au moins trois joueurs classés FIDE. Pour cela :

• on détermine le classement moyen de l'opposition (les joueurs classés) lors du tournoi, R_c (c pour compétition). Dans un système suisse, c'est simplement la moyenne des classements des adversaires déjà classés FIDE. Dans le cas d'un tournoi toutes rondes, la formule du calcul de R_c est donnée sur le site de la FIDE ;
• on calcule le pourcentage de gain contre ces adversaires (la performance du joueur), p, c’est-à-dire la somme des points obtenus divisée par le nombre de parties ;
• on détermine d(p) en fonction de la table FIDE dont un extrait est donné à droite (les valeurs de 800 et - 800 pour p=1 ou 0 sont arbitraires).

Pour obtenir le classement, R_u, du joueur pour la compétition :

• si p = 0,5 (le joueur marque 50 % des points), alors R_u = R _c (le classement de l'opposition qu'il a rencontrée)
• si p < 0,5 (le joueur marque moins de 50 % des points), alors R_u = R_c + d(p) pour un système suisse (pour un tournoi toutes rondes, la formule est donnée sur le site de la FIDE).
• si p > 0,5 (le joueur marque plus de 50 % des points), alors R_u = R_c + 15 points par demi-point obtenu au-dessus de 50 %, c'est à dire R_u = R_c + 15 x (Nombre de victoires − Nombre de défaites).

Dès qu’il existe 9 parties jouées contre des joueurs classés, le premier classement publié, Rn, sera égal à la moyenne pondérée des R_u de chaque tournoi, arrondie à l’entier le plus proche, si toutefois celle-ci dépasse 1000 (seuil plancher au 1^er juillet 2012).

Par exemple, un joueur qui joue vingt parties, contre des joueurs classés, dans trois tournois :

• dans le premier, il réalise un R_u= 2280 sur 5 parties
• dans le second, R_u= 2400 sur 10 parties
• dans le troisième, R_u= 2000 sur 5 parties

Son premier classement publié sera :

• Rn = ( 2280 × 5 + 2400 × 10 + 2000 × 5 ) / 20 = 2270.

Joueurs ayant déjà un classement

Pour chaque partie jouée contre un joueur classé FIDE (dans un système suisse, on ne tient pas compte des résultats contre les joueurs non classés) :

• on détermine la différence D de classement (au début du tournoi) entre le joueur adverse et le sien (ramenée à 400 si elle dépasse 400 depuis le 1^er juillet 2009 - au lieu de 350 avant cette date)
• on détermine p(D) à l’aide de la table FIDE (obtenue par la formule $p (D) = \frac{1}{1 + 10^{\frac{-D}{400}}}$)
• on détermine un coefficient K qui vaudra :
  • K=30 jusqu’à la 30^e partie du joueur, sinon
  • K=15 pour un classement Elo en dessous de 2400 Elo, sinon
  • K=10 pour un classement Elo au-dessus de 2400.

Soit W le résultat (c'est à dire le score) contre l’adversaire classé (W=1, ½ ou 0), le nouveau classement sera :

$E_{n+1} = E_n + K \times (W - p(D))$

($E_n$ est le classement intermédiaire avant de rencontrer le joueur classé.)

Par exemple, si un joueur classé 2600 gagne contre un joueur classé 2700 (Données : D = 2600 - 2700 = -100; p(D) = 36 %; K = 10; W = 1), son nouveau classement sera :

2600 + 10 x ( 1 - 0,36 ) = 2606,4.

Pour la publication, on arrondira à l’entier le plus proche (2606).

Dans un tournoi toutes rondes, on tient compte des joueurs non classés seulement après qu'ils ont joué contre tous les joueurs classés. Pour chacun de ces joueurs non classés, on calcule un classement estimé, Ru (la procédure en plusieurs étapes est décrite le site de la FIDE), puis on utilise Ru pour calculer la différence D (que l'on plafonne à 400) entre le joueur classé et le joueur non classé.

Depuis juillet 2012, le classement FIDE est mis à jour tous les mois, et publié tous les 1^er du mois. Si un joueur a moins de quatre parties classées sur une période d’un an, il est considéré comme inactif. Si le classement passe en dessous du seuil FIDE (1000), le joueur est retiré de la liste et à nouveau considéré comme un non-classé.

Performance Elo

On utilise la notion de performance Elo pour caractériser la force d’un joueur dans un tournoi, en fonction de la moyenne des classements Elo des adversaires (R_c) et du résultat contre ceux-ci (p), elle est aussi parfois employée comme système de départage d’un tournoi au système suisse :

• R_p=R_c + d(p)

Voici un exemple pour un joueur initalement classé 1500 :

Adversaire n°	Elo	Résultat
1	2010	-
2	1150	+
3	1490	-
4	1260	+
5	1420	+
6	1510	+
7	1580	=

Le score de la première partie est rejeté car non compatible selon la règle des 400 points.

R_c = 1402

Score sur les parties compatibles = 4 + 0,5 -1 = 3, 5 d'où p = 3,5 / 6 = 58,33% et d(58,33%) = 60

Performance Elo réalisée: R_p=1402 + 60 = 1462.

Il est à noter que si la première partie avait été prise en compte, la performance Elo aurait semblé atteindre 1489 + d (50%) = 1489 > 1462, ce qui illustre le bien-fondé de la règle des 400 points: ce n'est pas en perdant des parties contre des joueurs bien mieux classés qu'on gagne des points Elo, de même que ce n'est pas en remportant des parties contre des joueurs bien moins classés qu'on perd des points Elo.

Autres classements

Nombre de classés FIDE par tranche de 10 points Elo (juillet 2009).

Les fédérations nationales utilisent souvent un système légèrement différent de celui de la Fédération internationale des échecs (FIDE).

Il existe souvent deux classements distincts : l’un au niveau international, géré par la FIDE, et dit « Classement FIDE » ou « Classement international », et un au niveau national, géré en France par la FFE, par la FQE au Québec, par la FCE au Canada et par la FSE en Suisse, dit « Elo national ». Un joueur peut disposer à la fois d’un classement international et d’un ou plusieurs classements nationaux qui évoluent indépendamment.

Jusqu’en 1993, le seuil minimal du classement FIDE était fixé à 2200, soit le niveau d’un candidat maître, les amateurs ne disposaient que du classement national. Il a été abaissé progressivement jusqu’à atteindre 1000 depuis le 1^er juillet 2012 ce qui est le niveau d’un débutant en tout début d'apprentissage, soit in fine la totalité des joueurs.

Depuis le 1^er juillet 2009, la différence maximale entre deux classements pour le calcul des points gagnés ou perdus après chaque partie a été ramenée à 400 points au lieu de 350 précédemment.

Classement en parties rapides et en blitz

En juillet 2012, la FIDE inaugure deux nouveaux classements, ceux de parties rapides et de blitz. Ils ne sont néanmoins par encore établi pour les 100 premiers mondiaux dont beaucoup ont peu joué à ces cadences.

Autre nouveauté de juillet 2012, le classement officiel qui était établi tous les trois mois et qui depuis septembre 2009 était devenu bimestriel, devient mensuel.

Niveau de jeu en fonction du nombre de points

Ces éléments sont donnés à titre indicatif. Les titres sont attribués par la FIDE en fonction de performances réalisées lors de compétitions et si le prétendant a obtenu un classement Elo requis. Ils sont ensuite acquis à vie et le classement d’un maître peut ensuite être inférieur à ce minimum.

• ≥ 1000 : Débutant (enfant)
• ≥ 1200 : Débutant (en Belgique l’elo minimum est de 1150)
• ≥ 1400 : Joueur amateur
• ≥ 1600 : Bon joueur
• ≥ 1800 : Très bon joueur
• ≥ 2000 : Niveau national
• ≥ 2100 : Maître FIDE féminin (MFF ou WF)
• ≥ 2200 : Candidat maître
• ≥ 2200 : Maître international féminin (MIF ou WIM)
• ≥ 2300 : Maître FIDE (F)
• ≥ 2300 : Grand maître international féminin (GMF ou WGM)
• ≥ 2400 : Maître international (MI)
• ≥ 2500 : Grand maître international (GMI)
• ≥ 2600 : les 200 meilleurs joueurs mondiaux
• ≥ 2700 : les 50 meilleurs joueurs mondiaux
• ≥ 2800 : Au 1^er février 2013, seuls six joueurs avaient dépassé les 2 800 points, soit avec indication de l'Elo le plus élevé :
  • Garry Kasparov a été le premier joueur à dépasser les 2 800 (en janvier 1990) ; Il atteignit 2 851 en juillet 1999 et janvier 2000),
  • Vladimir Kramnik (maximum 2 811 en janvier 2002).
  • Veselin Topalov (maximum 2 813 en juillet 2006),
  • Viswanathan Anand (maximum 2 817 en mars 2011),
  • Levon Aronian (maximum 2 825 en mai 2012),
  • Magnus Carlsen (record 2 872 en février 2013),

Le titre de maître Fide (2300) et celui de maître Fide féminin (2100) sont acquis à vie dès que la cote Elo est atteinte sans faire de norme. Pour les titres de maîtres internationaux ou grands maîtres internationaux mixtes ou féminins des normes doivent être réalisées .

Les numéros un mondiaux

Depuis l’adoption du classement par la FIDE en 1970, seuls sept joueurs ont été classés à la première place. Garry Kasparov est le joueur étant resté numéro un le plus longtemps. Il faut noter que Bobby Fischer a cessé de participer aux compétitions après août 1972 mais est resté numéro un jusqu'en 1975. De même, Garry Kasparov s'est retiré du circuit professionnel en mars 2005 et a conservé son classement Elo pendant un an (jusqu'en février 2006).

De 1972 à 1980, les classements Elo étaient publiés une fois par an. De janvier 1981 à juillet 2000, il paraissaient deux fois par an (tous les six mois : en janvier et en juillet). De juillet 2000 à juillet 2009, ils étaient publiés quatre fois par an (un classement chaque trimestre : en janvier, avril, juillet et octobre). De septembre 2009 à juillet 2012, ils paraissaient tous les deux mois. Depuis août 2012 la parution est mensuelle.

De 1970 à janvier 2006

Période	Nom	Elo max
janvier 1970 – janvier 1975	Bobby Fischer	2785
janvier 1976 – juillet 1983	Anatoli Karpov	2725
janvier 1984 – juillet 1995	/ Garry Kasparov	2815
janvier 1996	Garry Kasparov Vladimir Kramnik	2775
juillet 1996 – janvier 2006	Garry Kasparov	2851

Depuis avril 2006

Période	Nom	Elo max
avril 2006 – janvier 2007	Veselin Topalov	2813
avril 2007 – octobre 2007	Viswanathan Anand	2801
janvier 2008	Viswanathan Anand Vladimir Kramnik	2799
avril 2008 – juillet 2008	Viswanathan Anand	2803
octobre 2008 – novembre 2009	Veselin Topalov	2813
janvier 2010 – septembre 2010	Magnus Carlsen	2826
novembre 2010	Viswanathan Anand	2804
janvier 2011	Magnus Carlsen	2814
mars 2011 – mai 2011	Viswanathan Anand	2817
depuis juillet 2011	Magnus Carlsen	2872

Le classement Elo maximum indiqué est celui de la période considérée (ce qui ne correspond pas toujours au meilleur classement Elo du joueur).

Classement récent

Liste des 10 premiers mondiaux au 1^er avril 2013

Rang	Ancien rang	Nom	Nation	Elo (variation)	Parties jouées	Né en
1	1	Magnus Carlsen	Norvège	2872 (=)	0	1990
2	3	Levon Aronian	Arménie	2809 (=)	0	1982
3	2	Vladimir Kramnik	Russie	2801 (-9)	6	1975
4	4	Teimour Radjabov	Azerbaïdjan	2793 (=)	0	1987
5	6	Sergueï Kariakine	Russie	2786 (=)	0	1990
6	7	Viswanathan Anand	Inde	2783 (-1)	6	1969
7	11	Fabiano Caruana	Italie	2772 (+12)	6	1992
8	8	Veselin Topalov	Bulgarie	2771 (=)	0	1975
9	9	Hikaru Nakamura	États-Unis	2767 (=)	0	1987
10	10	Shakhriyar Mamedyarov	Azerbaïdjan	2766 (=)	0	1985

Moyenne Elo : 2792

Cette liste est établie tous les mois et les variations concernent la différence avec la liste du 1^er mars 2013.
Source : (en) Top10 Hommes sur fide.com.

Autour du classement Elo

Le film Le Réseau social montre Mark Zuckerberg cherchant à classer sur un axe unique d'attractivité tous les visages d'un trombinoscope alors que les avis de ses amis ne peuvent les classer que deux par deux, et s'inspirer à cette fin de la formule de calcul d'Elo, que l'on voit brièvement au tableau à un moment du film.

Annexes

Bibliographie

• (en) Arpad Elo, The Rating of Chessplayers, Past and Present, New York, Arco Pub., 1978, 206 p. (ISBN 0-668-04721-6 et 9780668047210) (OCLC 4504131) 
• « Jeux et sports : le problème des classements », Rémi Coulom, Pour la Science, juillet 2010, pages 20 à 27.

Articles connexes

• Catégorie d'un tournoi
• Classement ECF
• Classement mondial de football Elo
• Classement mondial féminin de la FIFA
• Classement Glicko
• Fédération internationale des échecs

Liens externes

• (en) Classement mixte des joueurs à plus de 2700 Elo, calculé selon les règles de la FIDE et actualisé partie par partie.
• (ru) Classement des 30 meilleures joueuses mondiales selon les règles de la FIDE et établi quotidiennement.