Quadrilatère
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En géométrie plane, un quadrilatère est un polygone à quatre côtés. Les trapèzes, parallélogrammes, losanges, rectangles, carrés et cerfs-volants sont des quadrilatères particuliers.
Autres appellations et étymologies[modifier | modifier le code]
Le mot « quadrilatère » provient du latin : quatuor, quatre, et latus, lateris, côté[1],[2]. Le mot équivalent d'origine grecque est tétrapleure (du pl. neutre τέσσαρα / téssara, « quatre »[3], et πλευρά / pleurá, « côté »)[4] ou tétragone (de γωνία / gōnía, angle »). Le mot tétragone était employé par Gerbert d'Aurillac[4] au Xe siècle et par Oresme[1] au XIVe siècle. Le terme quadrilatère est introduit en 1554 par Peletier[1],[2]. Certains auteurs employaient le mot « quadrangle » (Alcuin, VIIIe siècle)[1],[4] ou « helmuariphe », terme d'origine arabe (Campanus, XIIIe siècle, et d'autres à la Renaissance)[1],[4]. Pour les Grecs, un quadrilatère avec un angle rentrant s'appelait un « koïlogone » (de κοῖλος / koīlos, « creux »)[1],[4], et certains appelaient « trapèze » un quadrilatère dont tous les côtés sont inégaux. « Tétragone » est employé par Euclide dans Les Éléments pour désigner le carré[1],[4].
Caractéristiques[modifier | modifier le code]
Un quadrilatère est la figure notée « ABCD » formée par :
- quatre points distincts A, B, C et D : les sommets du quadrilatère ;
- quatre segments [AB], [BC], [CD] et [DA] : les côtés du quadrilatère.
Les sommets A et C sont dits opposés, ainsi que les sommets B et D.
Les diagonales [AC] et [BD] joignent les sommets opposés.
Un quadrilatère est dit :
- croisé, si deux côtés opposés se coupent;
- non croisé, ou simple, dans le cas contraire.
Selon le théorème sur la somme des angles d'un polygone, la somme des mesures entre 0° et 360° des angles intérieurs d'un quadrilatère non croisé vaut 360°.
Note : les 4 permutations circulaires des lettres ABCD et les 4 permutations circulaires des lettres DCBA définissent le même quadrilatère. Les 16 autres permutations définissent deux autres quadrilatères.

Intérieur[modifier | modifier le code]
Comme toute courbe de Jordan, la réunion des côtés d'un quadrilatère non croisé découpe le plan en deux zones, une, bornée, l'intérieur du quadrilatère et l'autre, l'extérieur du quadrilatère.
Un point M est intérieur au quadrilatère non croisé ABCD si et seulement si les quatre triangles MAB, MBC, MCD, MDA sont orientés dans le même sens.
Cela se traduit par le fait que les déterminants sont de même signe.
Condition d'existence d'un quadrilatère de longueurs de côtés donnés[modifier | modifier le code]
Quatre réels strictement positifs sont les longueurs des côtés consécutifs d'un quadrilatère dont trois sommets ne sont pas alignés si et seulement si [5].
Quadrilatère convexe[modifier | modifier le code]
Caractérisations[modifier | modifier le code]
En géométrie élémentaire, une grande place est accordée aux quadrilatères convexes.
Un quadrilatère est convexe si et seulement si :
- quel que soit le côté que l'on choisit, le quadrilatère est entièrement inclus dans un demi-plan dont la frontière porte ce côté
ou
- c'est un quadrilatère non croisé dont tous les angles sont saillants
Ces caractérisations sont générales à tout polygone convexe. Dans le cas particulier du quadrilatère, il existe d'autres caractérisations : un quadrilatère est convexe si et seulement si :
- les diagonales se rencontrent.
- les diagonales sont situées à l'intérieur du quadrilatère
- une droite du plan ne passant pas par un sommet rencontre au plus deux côtés du quadrilatère.
Un quadrilatère simple est non convexe si l'une de ses diagonales est située à l'extérieur du quadrilatère.
Aire[modifier | modifier le code]
L'aire d'un quadrilatère convexe est égale au demi-produit des longueurs des diagonales multiplié par le sinus de l'angle qu'elles forment.
Intérieur[modifier | modifier le code]
L'intérieur d'un quadrilatère convexe ABCD peut être défini comme l'intersection des demi-plans ouverts délimités par (AB), par (BC), par (CD) et par (DA) et contenant respectivement chacun les points C, D, A et B.
Cela se traduit par le fait que les quatre produits sont strictement positifs.

Théorème de Fermat pour un quadrilatère[modifier | modifier le code]
Le point d'intersection des diagonales d'un quadrilatère convexe est le point du plan pour lequel la somme des distances aux quatre sommets est minimale et ce minimum est strict[5].
Avec les notations de la figure, on utilise l'inégalité triangulaire dans les triangles AMC et BMD.
Quadrangle et quadrilatère[modifier | modifier le code]
Un quadrilatère dérive directement d'un quadrangle par le regroupement des sommets en deux paires. Pour chaque paire, les deux sommets sont dits opposés et le segment qui les joint (côté du quadrangle) n'est plus considéré comme un côté, mais comme une diagonale du quadrilatère.
Donc la première chose à savoir sur les quadrilatères quelconques, c'est que, contrairement aux triangles, la donnée de leurs sommets ne suffit pas à les définir (mais définit un quadrangle, sous certaines conditions).
En effet, considérons quatre points A, B, C et D (non alignés trois à trois pour éviter certains problèmes).
Ces quatre points sont les extrémités de six segments distincts : les six côtés du quadrangle : [AB], [AC], [AD], [BC], [BD] et [CD].
Ces segments peuvent être assemblés, quatre à quatre, pour former trois quadrilatères distincts (et trois seulement) :
- [AB] + [BC] + [CD] + [DA] noté ABCD ;
- [AB] + [BD] + [DC] + [CA] noté ABDC ;
- [AC] + [CB] + [BD] + [DA] noté ACBD.
Les quatre segments utilisés par le quadrilatère sont ses côtés ; les deux autres segments sont ses diagonales.
Notation : ainsi ABCD est une notation commune pour définir un quadrangle ou un quadrilatère.
Cependant si l'ordre des points est indifférent pour un quadrangle, il doit en revanche être respecté (à une rotation ou un retournement près) pour conserver un même quadrilatère.
Il existe 24 arrangements des quatre points A, B, C et D basés sur le même quadrangle. Il y a trois quadrilatères ABCD, ACBD, ABDC.
Le même quadrilatère ABCD peut donc s'écrire ABCD, BCDA, CDAB, DABC dans un sens ; DCBA, CBAD, BADC, ADCB dans l'autre sens.
Quadrangles et quadrilatères complets[modifier | modifier le code]
- Un quadrangle complet est l'ensemble de 4 points et des 6 droites qui les relient 2 à 2.
- Un quadrilatère complet est l'ensemble de 4 droites et de leurs 6 points d'intersection 2 à 2.
Typologie des quadrilatères[modifier | modifier le code]
Les quadrilatères quelconques offrent relativement peu d'intérêt, mais permettent de voir ce qui se cache derrière les définitions des quadrilatères particuliers bien connus (trapèze, parallélogramme, rectangle, losange, carré, cerf-volant, pseudo-carré, etc.).
-
Diagramme de Venn de différents types de quadrilatères convexes.
-
Diagramme d'Euler de différents types de quadrilatères.
-
Diagramme de Hasse de différents types de quadrilatères.
Quand on cherche à classer les quadrilatères en leur imposant des propriétés particulières, on obtient les classes énumérées ci-dessous.

Diagonales perpendiculaires[modifier | modifier le code]
Un quadrilatère dont les diagonales (éventuellement prolongées) sont perpendiculaires est appelé un quadrilatère orthodiagonal. L'aire d'un tel quadrilatère non croisé est (où D et d sont les longueurs des diagonales), même dans le cas non convexe.
Cette catégorie ne présente pas de régularité d'aspect.
Parmi les quadrilatères convexes dont les diagonales sont perpendiculaires, on peut noter :
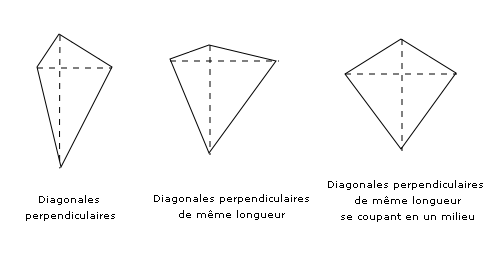
- ceux qui ont deux côtés consécutifs égaux : les cerfs-volants (dont les losanges) ;
- ceux dont les diagonales sont de même longueur : les pseudo-carrés.
Côtés égaux deux à deux[modifier | modifier le code]

On n'obtient pas toujours un parallélogramme. Pour obtenir un parallélogramme, il faut que le quadrilatère soit en outre convexe et que les côtés opposés soient égaux. Si le quadrilatère n'est pas convexe et les côtés opposés sont égaux deux à deux, on obtient un quadrilatère croisé : l'antiparallélogramme.
Si les côtés égaux sont consécutifs deux à deux, on retombe sur le cerf-volant.
Côtés parallèles[modifier | modifier le code]
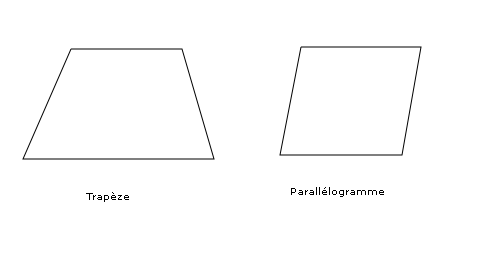
On retrouve là deux classes intéressantes de quadrilatères convexes : les trapèzes et, parmi eux, les parallélogrammes.
Parmi les trapèzes particuliers, on trouve le trapèze isocèle dont les côtés non parallèles sont de même longueur et le trapèze rectangle qui possède deux angles droits.
Parmi les parallélogrammes particuliers on trouve les rectangles (parallélogrammes à angles droits), les losanges (parallélogrammes à côtés adjacents égaux) et les carrés (à la fois rectangles et losanges).

Ainsi, selon cette classification, le carré est le quadrilatère le plus riche en propriétés. Il est aussi l'unique solution du problème isopérimétrique pour les quadrilatères. C'est-à-dire que, parmi tous les quadrilatères de même périmètre, le carré est celui qui possède la plus grande surface.
Quadrilatères inscriptibles[modifier | modifier le code]
Les quadrilatères inscriptibles sont les quadrilatères dont les sommets sont situés sur un cercle, ou cocycliques.

Le théorème de l'angle inscrit permet la caractérisation suivante : un quadrilatère est inscriptible si et seulement s’il possède deux angles opposés égaux ou supplémentaires : quand les angles sont supplémentaires il s'agit d'un quadrilatère convexe, et quand les angles sont égaux, il s'agit d'un quadrilatère croisé.
En particulier, un trapèze isocèle, un rectangle sont des quadrilatères inscriptibles.
Le théorème de Ptolémée permet d'affirmer qu'un quadrilatère convexe est inscriptible si, et seulement si, le produit des longueurs des diagonales est égal à la somme des produits des longueurs des côtés opposés.
La formule de Brahmagupta donne l'aire d'un quadrilatère convexe inscriptible en ne connaissant que la longueur de ses côtés.
où est le demi-périmètre du quadrilatère, a, b, c et d sont les longueurs de ses côtés et S son aire.
Quadrilatères circonscriptibles[modifier | modifier le code]
Les quadrilatères circonscriptibles sont ceux admettant un cercle inscrit, c'est-à-dire tangent aux quatre côtés. Cela n'est possible que si les quatre bissectrices sont concourantes en un point qui est le centre du cercle inscrit.
Le théorème de Pitot caractérise les quadrilatères circonscriptibles : un quadrilatère dont les côtés ont pour longueurs successives a, b, c, et d est circonscriptible si et seulement si les sommes des côtés opposés sont égales entre elles, à savoir
où p est le demi-périmètre du quadrilatère.
Les cerfs-volants, les losanges et les carrés sont des exemples de quadrilatères circonscriptibles.
Quadrilatères bicentriques[modifier | modifier le code]

Les quadrilatères bicentriques sont à la fois inscriptibles et circonscriptibles, et héritent donc des caractéristiques des deux catégories précédentes.
La distance entre le centre du cercle circonscrit et le centre du cercle inscrit est l'objet du théorème de Fuss.
On peut appliquer aux deux cercles respectivement inscrits et circonscrits à un quadrilatère bicentrique le théorème de Poncelet qui permet de construire une infinité d'autres quadrilatères bicentriques relativement à ces cercles, comme illustré par la figure ci-contre.
Bimédianes, médianes, et centre de gravité[modifier | modifier le code]
Les deux bimédianes d'un quadrilatère sont les segments joignant les milieux de deux cotés opposés [5].
Les quatre médianes sont les segments joignant un sommet au centre de gravité du triangle formé par les trois autres sommets [5].
Le centre de gravité d'un quadrilatère est l'isobarycentre des sommets.
D'après la propriété d'associativité du barycentre, le centre de gravité est le milieu des bimédianes, le milieu du segment joignant les milieux des diagonales, et il se trouve aux trois quarts des médianes, en partant des sommets.
Attention, contrairement au cas du triangle, le centre de gravité d'une plaque quadrilatérale homogène est différent de l'isobarycentre des sommets, sauf si est le point d'intersection des diagonales (auquel cas le quadrilatère est un parallélogramme). On a en effet (théorème de Wittenbauer).
Notes et références[modifier | modifier le code]
- « Étymologie des maths ».
- Informations lexicographiques et étymologiques de « quadrilatère » dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- Anatole Bailly ; 2020 : Hugo Chávez, Gérard Gréco, André Charbonnet, Mark De Wilde, Bernard Maréchal & contributeurs, « Le Bailly », (consulté le ).
- Emile Fourrrey, Curiosités géométriques, (lire en ligne), p. 49.
- Mohammed AASSILA, 1000 challenges mathématiques, géométrie, Ellipses, , p. 341, 347, 348, 351
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Quadrilatère complet
- Théorème de Pitot
- Relation d'Euler dans le quadrilatère
- Formule de Bretschneider donnant l'aire d'un quadrilatère non croisé
- Parallélogramme de Wittenbauer