Nombre triangulaire


En arithmétique, un nombre triangulaire est un cas particulier de nombre polygonal. Il correspond à un entier naturel non nul égal au nombre de pastilles dans un triangle construit à la manière des deux figures de droite. La seconde montre que le septième nombre triangulaire — celui dont le côté porte 7 pastilles — est 28. Une définition plus formelle de cette suite d'entiers s'obtient par récurrence : le premier nombre triangulaire est 1, et le n-ième est la somme de n et du précédent. Les dix premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 (suite A000217 de l'OEIS). Il existe différentes manières de calculer le n-ième nombre triangulaire ; l'une d'elles est graphique et s'obtient par un raisonnement d'arithmétique géométrique. On trouve, si tn désigne le n-ième nombre triangulaire :
où est le symbole du coefficient binomial. Les nombres triangulaires sont donc ceux de la troisième colonne du triangle de Pascal.
Cette formule est ancienne — on la doit à l'école de Pythagore — et probablement connue depuis le début du Ve siècle av. J.-C.
Elle est citée par Alcuin au IXe siècle dans un recueil de récréations mathématiques[1].
Définition et calculs[modifier | modifier le code]
Définitions[modifier | modifier le code]

Formellement, les nombres triangulaires sont définis à partir d'une suite, notée (tn) dans cet article, où n est un indice[2] parcourant les entiers strictement positifs :
Définition[3] — Pour tout entier n strictement positif, le n-ième nombre triangulaire est[4] la somme des entiers de 1 à n.
Une autre manière de définir cette suite est de le faire par récurrence. Les deux formulations sont équivalentes :
Définition[5] — La suite des nombres triangulaires est définie par :
Chez les Pythagoriciens, le quatrième nombre triangulaire, c'est-à-dire 10, est nommé tetraktys. Il dispose d'une dimension symbolique[6].
Remarque : Le choix de ne pas définir le nombre triangulaire d'indice 0 se justifie historiquement, le zéro n'existant pas chez les Grecs de l'Antiquité. Cette convention est choisie pour certaines présentations didactiques[3]. Elle est aussi choisie historiquement dans l'encyclopédie de Diderot et D'Alembert pour tous les nombres figurés[7]. Mais elle n'est pas toujours suivie. Si l'on admet 0 comme nombre triangulaire, tout entier positif est somme de trois nombres triangulaires. Cette raison pousse Fermat et Gauss à choisir d'accepter 0 comme nombre triangulaire[8].
Méthodes de calcul[modifier | modifier le code]

Une vieille méthode de calcul provient de l'école pythagoricienne[9]. Les Grecs de cette époque usaient de géométrie pour résoudre les questions de cette nature. Cette approche est qualifiée d'arithmétique géométrique. La figure de droite permet de comprendre comment ils calculaient le 8e nombre triangulaire. La zone rouge de la figure correspond à ce nombre, c'est-à-dire la somme 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8. À cette zone rouge, on accole la zone bleue de la figure, contenant exactement le même nombre de pastilles que la rouge. La zone bleue et rouge contient un nombre de pastilles égal à deux fois le 8e nombre triangulaire. Or cette zone est un rectangle de base 9 et de hauteur 8. Le double du 8e nombre triangulaire est égal à 8 × 9 = 72 donc ce 8e nombre est égal à 36. On retrouve bien la formule annoncée en introduction :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | |||||||
| 2 | 1 | 2 | 1 | ||||||
| 3 | 1 | 3 | 3 | 1 | |||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Cette formule se réinterprète comme l'expression du n-ième nombre triangulaire sous la forme d'un coefficient binomial :
Il en existe une preuve directe sans mots, par bijection entre les pastilles du triangle et les paires contenues dans un ensemble à n + 1 éléments[10].
Pour d'autres preuves, purement algébriques, voir l'article Somme (arithmétique), § « Somme des premiers entiers ».
Résultats géométriques[modifier | modifier le code]
Les Grecs de l'école de Pythagore n'avaient pas connaissance des théorèmes fondamentaux de l'arithmétique élémentaire, comme le lemme d'Euclide, le théorème de Bachet-Bézout ou encore le théorème fondamental de l'arithmétique. Ils ont développé une arithmétique différente et les résultats présentés ici sont un peu à l'image de leur conception de l'arithmétique[11]. Néanmoins, comme il n'existe pas de texte directement écrit sur cette question par les membres de cette école, il est difficile de relier des résultats précis à des dates ou des noms de membres de l'école[12], ainsi que d'être catégorique sur le fait qu'un résultat était bien connu d'eux.
Somme de deux nombres triangulaires consécutifs[modifier | modifier le code]

La figure de droite montre que la somme du quatrième et du cinquième nombre triangulaire forme le cinquième carré parfait, c'est-à-dire 25. Ce résultat n'est pas uniquement vrai pour la valeur cinq :
Proposition — Pour tout entier n > 1, la somme des deux nombres triangulaires d'indices n et n – 1 est égale à n2.
La formule précédente permet d'établir ce résultat :
Un nombre triangulaire est somme de quatre nombres triangulaires[modifier | modifier le code]
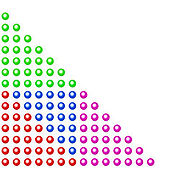

Les deux graphiques ci-contre indiquent que le n-ième nombre triangulaire est somme de quatre nombres triangulaires. Ceci est vrai quelle que soit la parité de l'indice n. En effet, t14 est la somme de trois fois t7 et de t6 et t15 est la somme trois fois t7 et de t8. Cette proposition s'exprime de la manière suivante :
Proposition[5] — À partir de l'indice 3, tout nombre triangulaire est somme de quatre nombres triangulaires. Plus précisément : pour tout entier n ≥ 2,
En effet :
Un carré parfait avec un unique nombre triangulaire[modifier | modifier le code]

La figure de droite montre qu'il est possible d’emboîter huit nombres triangulaires d'indice 7 pour former un carré de côté 15, auquel il manque la pastille centrale, en gris sur la figure ; résultat qui se généralise à tous les carrés de nombres impairs :
Proposition[5] — Pour tout entier n > 0, le carré parfait (2n + 1)2 est la somme de 8 fois tn et de 1 :
En effet, ce résultat est directement l'application d'une identité remarquable :
Cube et nombre triangulaire[modifier | modifier le code]
Un autre résultat traite des cubes. Il s'énonce ainsi :
Proposition[5] — Si n est un entier supérieur à 2, la différence entre les carrés des nombres triangulaires d'indices n et n – 1 est égale au cube de n.
Il est redécouvert par le mathématicien perse Al-Karaji[13], qui le démontre sur l'exemple n = 10 en considérant des gnomons et l'exprime d'une manière équivalente :
Proposition — Si n est un entier strictement positif, la somme des n premiers nombres cubiques est le carré du n-ième nombre triangulaire.
Autres propriétés[modifier | modifier le code]
Généralisations[modifier | modifier le code]
Si, au lieu de calculer la somme des n premiers nombres entiers strictement positifs, on calcule les n premiers carrés strictement positifs que l'on appelle cn, on obtient :
L'intuition de l'exactitude de cette formule est donnée par la preuve sans mots suivante[14] :

Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Il est aussi possible de généraliser en considérant le nombre de points sn,d contenus dans un simplexe dont les côtés sont de longueurs n, dans un espace de dimension d. On obtient :
Entier somme de trois nombres triangulaires[modifier | modifier le code]
En 1638, Fermat affirma détenir une preuve du fait que tout entier est somme de trois nombres triangulaires (à condition de considérer zéro comme un nombre triangulaire) et même d'une généralisation (le théorème des nombres polygonaux de Fermat, finalement démontré par Cauchy en 1813) et proclama son intention d'écrire un livre qui révolutionnerait cette partie de l'arithmétique[15], mais aucun livre ne parut[16]. En 1796[17], Gauss découvrit la preuve suivante[8].
La démonstration ici n'est pas géométrique. L'arithmétique telle qu'on la concevait à l'époque de Pythagore est impuissante pour prouver des résultats de cette nature. La partie difficile de la preuve est le théorème des trois carrés de Legendre, qui a pour conséquence que tout entier positif congru à 3 modulo 8 est somme de trois carrés parfaits. Soit M un nombre entier positif, 8M + 3 est somme de trois carrés. De plus chaque carré de la somme est impair, sinon leur somme ne serait pas congrue à 3 modulo 4. On en déduit l'existence de trois entiers x, y et z tels que :
Cette dernière égalité implique le résultat recherché : M est la somme des trois nombres triangulaires d'indices x, y et z.
Notes et références[modifier | modifier le code]
- « Les propositions d'Alcuin », sur récréomath, proposition 42. "Des barreaux d'une échelle".
- Le terme d'indice est celui souvent utilisé pour les suites : Axel Delmotte, William Seck et Hubert Silly, Réussir les tests d'entrée des 3e cycles et écoles de gestion, Jeunes Editions, 2005 (ISBN 978-2844725769), p. 67. D'autres auteurs[Lesquels ?] parlent néanmoins de rang et non pas d'indice.
- Gérard Villemin Nombre triangulaire Nombres - Curiosités, théorie et usages (2007)
- C'est donc le prototype de la somme des termes d'une suite arithmétique.
- Gérard Villemin Nombre triangulaire Nombres - Curiosités, théorie et usages (2007)
- (en) Walter Burkert, Lore and Science in Ancient Pythagoreanism, HUP, (ISBN 978-0674539181, lire en ligne), p. 463[Information douteuse].
- Denis Diderot Jean le Rond D'Alembert Encyclopédie ou dictionnaire raisonné des sciences des arts et des métiers (1781)
- C. F. Gauss, Recherches arithmétiques, p. 353 de la traduction de 1807.
- (en) Thomas Little Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, CUP, (1re éd. 1921) (ISBN 978-1-108-06306-7, lire en ligne), p. 76-77.
- Cette preuve de (en) Loren C. Larson, « A Discrete Look at 1 + 2 + ⋯ + n », College Mathematics Journal (en), vol. 16, no 5, , p. 369-382 (p. 375, figure 7) est reproduite par (en) Claudi Alsina et Roger B. Nelsen, Charming Proofs : A Journey Into Elegant Mathematics, MAA, (lire en ligne), p. 6 et par (en) Roger B. Nelsen, « Visual Gems of Number Theory », dans Arthur T. Benjamin et Ezra Brown, Biscuits of Number Theory, MAA, (lire en ligne), p. 53.
- Burkert 1972, p. 427-446.
- Dans Burkert 1972, p. 439, on trouve :[Information douteuse] « The only certainty about the discovery of irrationality is that Theodorus of Cyrene proved that √n (for n = 3, ... 17 and not a perfect square) is irrational. »
- A. Dahan-Dalmedico et J. Peiffer, Une histoire des mathématiques : Routes et dédales, [détail des éditions], p. 90.
- Elle provient de (en) Roger B. Nelsen, Proofs without Words : Exercises in Visual Thinking, MAA, , 152 p. (ISBN 978-0-88385-700-7, lire en ligne).
- Paul Tannery et Charles Henry, Œuvres de Fermat, t. 3, 1896, p. 252 : Commentaire de Bachet sur IV, 31.
- Joseph Louis Lagrange, « Démonstration d'un théorème d'arithmétique », Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Berlin, 1770, p. 123-133 – Œuvres complètes, tome 3, p. 189-201.
- « ΕΥΡΗΚΑ. num. = Δ + Δ + Δ », Journal de Gauss, 10 juillet 1796 [v. o.], [v. f.].
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Équation de Ramanujan–Nagell
- Ensemble triangulaire
- Nombre ennéagonal centré (sous-suite des nombres triangulaires d'indices congrus à 1 modulo 3, c'est-à-dire les nombres triangulaires congrus à 1 modulo 9 — les autres étant divisibles par 3)
- Nombre hexagonal (sous-suite des nombres triangulaires d'indices impairs)
- Nombre triangulaire carré
- Nombre triangulaire centré
- Nombre tétraédrique
- Nombre poli (différence de deux nombres triangulaires)
Bibliographie[modifier | modifier le code]
(en) George E. Andrews, « EϒPHKA! num = Δ + Δ + Δ », J. Number Theory, vol. 23, no 3, , p. 285-293 (lire en ligne)














