Ouverture (photographie)


L'ouverture d'un objectif photographique est le réglage qui permet d'ajuster le diamètre d'ouverture du diaphragme. Elle est caractérisée par N qui est le nombre d'ouverture[1] ou ouverture géométrique[2](elle est aussi fréquemment notée par le quotient « f / N »). Ce nombre sans dimension est défini comme le rapport du diamètre d de la pupille d'entrée à la focale f (distance focale image, positive, ici notée f pour simplifier les écritures).
- .
À focale constante, l'augmentation du nombre d'ouverture est la conséquence de la fermeture du diaphragme : elle a pour effets la réduction de l'éclairement du capteur ou de la pellicule, l'augmentation de la profondeur de champ et, dans une moindre mesure, la réduction des aberrations géométriques et chromatiques, l'augmentation de l'influence de la diffraction.
Les fabricants indiquent toujours l'ouverture utile[3] ou pleine ouverture de l'objectif : elle est fréquemment gravée sur la partie frontale de l'objectif et indique le nombre d'ouverture pour une ouverture maximale du diaphragme ; plus ce nombre est petit, plus l'objectif est lumineux.
L'ouverture relative est tantôt définie de façon identique au nombre d'ouverture[3],[4], tantôt comme son inverse[1],[5],[6], alors exprimée sous la forme du rapport « 1 : N » où N est le nombre d'ouverture.
L'indice d'ouverture utilise une échelle logarithmique : .
Il faut éviter la confusion avec l'ouverture numérique qui désigne tout autre chose.
Notations[modifier | modifier le code]
Plusieurs notations sont utilisées pour donner la valeur de l'ouverture. Par exemple, pour exprimer qu'un objectif est utilisé à une ouverture de 2,8, on trouvera les notations suivantes.
- N = 2,8 : la notation utilisée dans cet article, qui se trouve aussi dans des ouvrages traitant d'optique photographique. Elle n'est quasiment jamais utilisée par les photographes.
- f/2,8 : la notation la plus courante. On écrira par exemple qu'une photo a été « prise à f/2,8 », et il est alors entendu qu'il s'agit de l'ouverture.
- F2.8 : dans des ouvrages et sites anglophones. Probablement issue d'une simplification de la notation précédente.
- 1:2.8 : utilisée par les fabricants pour exprimer l'ouverture maximale des objectifs. Il s'agit de l'ouverture relative c'est-à-dire de l'inverse du nombre d'ouverture.
- 2.8 : lorsqu'il n'y a pas d'ambiguïté, la seule valeur numérique peut suffire. Utilisée par exemple sur les bagues de diaphragme des objectifs qui en sont pourvus.
À propos de la notation « f/2,8 », on peut remarquer qu'il s'agit de l'expression du diamètre de la pupille d'entrée (d = f/N), et que dans cette expression f désigne la distance focale. En pratique, cette signification est souvent ignorée, et « f/ » est considéré comme un préfixe introduisant le nombre d'ouverture. D'où le nom f-number (littéralement : « nombre f ») utilisé en anglais pour désigner le nombre d'ouverture.
Régulation de l'exposition[modifier | modifier le code]

Les surfaces sensibles, qu'il s'agisse de pellicules argentiques ou de capteurs électroniques, réagissent selon l'exposition lumineuse , produit de l'éclairement reçu et du temps de pose (vitesse d'obturation ou durée d’exposition) : .
Le diaphragme arrête une partie de la lumière quand on le ferme. Il permet de modifier l'éclairement reçu par la surface sensible. Pour une mise au point à l'infini, l'éclairement reçu par le capteur ou la pellicule est donné par (détails des calculs plus loin) :
avec :
- la luminance de l'objet photographié (cd·m−2),
- le facteur de transmission de l'objectif,
- le nombre d'ouverture.
L'éclairement de la surface sensible est donc inversement proportionnel au carré du nombre d'ouverture N. L'exposition peut ainsi être modifiée soit par modification de l'ouverture, soit par modification du temps de pose. Dans le cas de poses longues, au lieu de diaphragmer pour que l'image ne soit pas surexposée, on peut utiliser un filtre à densité neutre.
Par convention, il a été établi une suite de nombres d'ouverture pour lesquels le passage à la valeur supérieure entraîne une division par deux de l'éclairement, Il s'agit d'une suite géométrique de raison √2. Les valeurs approchées de cette suite sont gravées sur la bague de réglage du diaphragme :
- 0,5 – 0,7 – 1 – 1,4 – 2 – 2,8 – 4 – 5,6 – 8 – 11 – 16 – 22 – 32 – 45 – 64 – 90 – 128 – ...
Pour faciliter la manipulation, le mécanisme actionné par la bague comporte souvent des crans correspondant aux repères. L'intervalle entre deux crans est abusivement mais communément appelé « diaphragme », plus souvent abrégé en « diaph » : « fermer de trois diaphs » revient à diviser l'éclairement reçu par le capteur par huit. Entre chaque repère, il peut exister un ou deux crans supplémentaires pour les valeurs intermédiaires. Ils donnent alors un réglage précis au demi-diaph ou au tiers de diaph. L'ouverture est généralement limitée à 16 ou 22 (voire 32 pour les grands formats) afin d'éviter une dégradation excessive de l'image du fait de la diffraction.
Notation APEX[modifier | modifier le code]
Dans le système APEX, l'ouverture est représentée en échelle logarithmique par l'indice d'ouverture Av, aussi notée AV (aperture value), définie par :
- ou . Ou bien, plus simplement : N = (√2) (ou √ ou ).
Augmenter l'indice d'ouverture AV d'une unité correspond alors à fermer d'un « diaph ». Les tableaux ci-dessous donnent les correspondances entre AV et nombres d'ouverture, pour des progressions par demi-diaphragme, tiers de diaphragme, quart de diaphragme et huitième de diaphragme. Les nombres d'ouverture dans ces tableaux sont présentés conventionnellement arrondis à deux chiffres significatifs[7].
Les tableaux de correspondance se lisent de gauche à droite selon les valeurs d'AV croissantes, de l'AV-2 à l'AV14 (plage de 17 AV), et par groupe de deux lignes. Sur la première ligne figure l'indice d'ouverture AV et sur la seconde, le nombre d'ouverture N correspondant. Il va de l'ouverture 0,5 à l'ouverture 128 (soit 17 ouvertures normalisées).
Le dernier tableau par huitième de diaphragme, destiné à relever les ouvertures maximum des objectifs qui ne correspondent pas à une valeur entière d'AV, va uniquement de l'ouverture 0,5 à l'ouverture 5,6 (plage de 8 AV).
| AV | −2 | −1½ | −1 | −½ | 0 | ½ | 1 | 1½ | 2 | 2½ | 3 | 3½ | 4 | 4½ | 5 | 5½ | 6 | 6½ | 7 | 7½ | 8 | 8½ | 9 | 9½ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0,5 | 0,6 | 0,7 | 0,8 | 1 | 1,2 | 1,4 | 1,7 | 2 | 2,4 | 2,8 | 3,4 | 4 | 4,8 | 5,6 | 6,7 | 8 | 9,5 | 11 | 13 | 16 | 19 | 22 | 27 |
| AV | 10 | 10½ | 11 | 11½ | 12 | 12½ | 13 | 13½ | 14 | |||||||||||||||
| N | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 108 | 128 |
| AV | −2 | −1⅔ | −1⅓ | −1 | −⅔ | −⅓ | 0 | ⅓ | ⅔ | 1 | 1⅓ | 1⅔ | 2 | 2⅓ | 2⅔ | 3 | 3⅓ | 3⅔ | 4 | 4⅓ | 4⅔ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0,5 | 0,56 | 0,63 | 0,7 | 0,8 | 0,9 | 1 | 1,1 | 1,2 | 1,4 | 1,6 | 1,8 | 2 | 2,2 | 2,5 | 2,8 | 3,2 | 3,5 | 4 | 4,5 | 5 |
| AV | 5 | 5⅓ | 5⅔ | 6 | 6⅓ | 6⅔ | 7 | 7⅓ | 7⅔ | 8 | 8⅓ | 8⅔ | 9 | 9⅓ | 9⅔ | 10 | 10⅓ | 10⅔ | 11 | 11⅓ | 11⅔ |
| N | 5,6 | 6,4 | 7,1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 28 | 32 | 36 | 40 | 45 | 51 | 57 |
| AV | 12 | 12⅓ | 12⅔ | 13 | 13⅓ | 13⅔ | 14 | ||||||||||||||
| N | 64 | 72 | 81 | 90 | 102 | 114 | 128 |
| AV | −2 | −1¾ | −1½ | −1¼ | −1 | −¾ | −½ | −¼ | 0 | ¼ | ½ | ¾ | 1 | 1¼ | 1½ | 1¾ | 2 | 2¼ | 2½ | 2¾ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0,5 | 0,54 | 0,59 | 0,65 | 0,7 | 0,77 | 0,84 | 0,92 | 1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,7 | 1,8 | 2 | 2,2 | 2,4 | 2,6 |
| AV | 3 | 3¼ | 3½ | 3¾ | 4 | 4¼ | 4½ | 4¾ | 5 | 5¼ | 5½ | 5¾ | 6 | 6¼ | 6½ | 6¾ | 7 | 7¼ | 7½ | 7¾ |
| N | 2,8 | 3,1 | 3,4 | 3,7 | 4 | 4,4 | 4,8 | 5,2 | 5,6 | 6,2 | 6,7 | 7,3 | 8 | 8,7 | 9,5 | 10,4 | 11 | 12 | 13 | 15 |
| AV | 8 | 8¼ | 8½ | 8¾ | 9 | 9¼ | 9½ | 9¾ | 10 | 10¼ | 10½ | 10¾ | 11 | 11¼ | 11½ | 11¾ | 12 | 12¼ | 12½ | 12¾ |
| N | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 | 35 | 38 | 41 | 45 | 49 | 54 | 59 | 64 | 70 | 76 | 83 |
| AV | 13 | 13¼ | 13½ | 13¾ | 14 | |||||||||||||||
| N | 90 | 99 | 108 | 117 | 128 |
| AV | −2 | −1⅞ | −1¾ | −1⅝ | −1½ | −1⅜ | −1¼ | −1⅛ | −1 | −⅞ | −¾ | −⅝ | −½ | −⅜ | −¼ | −⅛ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0,5 | 0,52 | 0,54 | 0,57 | 0,59 | 0,62 | 0,65 | 0,68 | 0,7 | 0,74 | 0,77 | 0,80 | 0,84 | 0,88 | 0,92 | 0,96 |
| AV | 0 | ⅛ | ¼ | ⅜ | ½ | ⅝ | ¾ | ⅞ | 1 | 1⅛ | 1¼ | 1⅜ | 1½ | 1⅝ | 1¾ | 1⅞ |
| N | 1 | 1,04 | 1,09 | 1,14 | 1,19 | 1,24 | 1,30 | 1,35 | 1,4 | 1,48 | 1,54 | 1,61 | 1,68 | 1,76 | 1,83 | 1,91 |
| AV | 2 | 2⅛ | 2¼ | 2⅜ | 2½ | 2⅝ | 2¾ | 2⅞ | 3 | 3⅛ | 3¼ | 3⅜ | 3½ | 3⅝ | 3¾ | 3⅞ |
| N | 2 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,1 | 3,2 | 3,4 | 3,5 | 3,7 | 3,8 |
| AV | 4 | 4⅛ | 4¼ | 4⅜ | 4½ | 4⅝ | 4¾ | 4⅞ | 5 | |||||||
| N | 4 | 4,2 | 4,4 | 4,6 | 4,8 | 5,0 | 5,2 | 5,4 | 5,6 |
Les valeurs de N par incrément de un quart de diaphragme et par incrément de un huitième de diaphragme ont été calculées à l'aide de la formule N = (√2) avec ¼ = 0,25 et ½ = 0,5 et ¾ = 0,75 puis arrondies à deux chiffres significatifs.
Pour les valeurs de N par incrément de un huitième de diaphragme, ⅛ = 0,125 et ⅜ = 0,375 et ⅝ = 0,625 et ⅞ = 0,875 puis arrondies à deux ou trois chiffres significatifs.
Ce dernier tableau par huitième de diaphragme permet de retrouver précisément le nombre de diaphragmes AV des ouvertures ne correspondant pas exactement à une valeur entière de AV, ce qui est très souvent le cas des ouvertures maximum des objectifs. Le tableau par tiers de diaphragme permet la même recherche. Sauf exception, les valeurs d'ouverture maximum se situent, le plus souvent, à une distance de ⅛, ¼, ⅓,⅜ ou ½ diaphragme d'une AV entière. Une fois l'AV de l'ouverture maximum précisément relevée, cette dernière peut ensuite être facilement comparée, en fraction de diaphragme, aux ouvertures normalisées bien connues.
Par exemple, une ouverture max de 1,1 est proche de 1,09 qui correspond une AV de ¼ de diaphragme. Cette AV est supérieure ¼ de diaphragme à l'AV 0 (ou inférieure de ¾ de diaphragme à l'AV 1). On peut donc dire que l'ouverture 1,1 est supérieure de un peu moins de ¾ de diaphragme à l'ouverture 1,4 (ou inférieure de un peu plus de ¼ de diaphragme à l'ouverture 1).
Autre exemple, à une ouverture max de 1,7 correspond à une AV de 1½. Elle est donc supérieure de ½ diaphragme à l'ouverture 2 (ou inférieure de ½ diaphragme à l'ouverture 1,4).
Pour les valeurs d'ouverture non présentes dans le tableau, telle l'ouverture 3,3, il reste toujours la possibilité de calculer l'AV à l'aide de la formule . Dans le cas de l'ouverture 3,3, diaphragmes. Elle est donc inférieure de 0,4 diaphragme à l'ouverture 2,8 (ou supérieure de 0,6 diaphragme à l'ouverture 4).
Encore un exemple, l'ouverture max de 1,8, très fréquente, est supérieure de ¼ de diaphragme à l'ouverture 2 (ou inférieure de ¾ de diaphragme à l'ouverture 1,4).
Dernier exemple, une ouverture max de 0,95, proche de 0,96, est supérieure de un peu plus de ⅛ de diaphragme à l'ouverture 1.
Ne pas oublier qu'aux valeurs croissantes des AV correspondent des valeurs d'ouverture décroissantes !
Ouverture photométrique (T-number)[modifier | modifier le code]
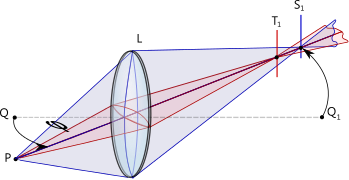
L'expression de l'exposition montre que celle-ci dépend de la transparence T de l'objectif. Il faudrait donc, en toute rigueur, connaître cette transparence pour déterminer l'exposition. En pratique, les différences de transparence d'un objectif à un autre sont souvent négligées[8]. Lorsqu'il importe de déterminer l'exposition avec une grande précision, il faut pourtant en tenir compte. Afin de limiter le nombre de paramètres à prendre en compte, l'ouverture et la transparence sont combinés en un seul paramètre appelé ouverture photométrique, défini comme l'ouverture géométrique que devrait avoir un objectif parfaitement transparent pour avoir la même luminosité que l'objectif considéré : sa valeur est toujours supérieure à celle de l'ouverture géométrique. L'ouverture photométrique est donc donnée par :
- .
L'expression de l’exposition devient alors :
- .
L'ouverture photométrique est généralement notée avec le préfixe « T/ ». Par exemple, « T/3.1 » signifie NT = 3,1. Il ne s'agit nullement d'une fraction, mais simplement d'une notation établie par analogie avec « f/ ».
Les objectifs destinés aux caméras cinématographiques sont souvent pourvus d'une échelle d'ouvertures photométrique en plus, ou à la place, de l'échelle d'ouvertures géométriques. Chaque objectif est étalonné individuellement[9].
Ouverture effective[modifier | modifier le code]
La formule précédente pour l'exposition est valable pour une mise au point à l'infini, et reste une très bonne approximation pour des distances de prise de vue supérieures à environ dix fois la distance focale. Cependant, en photographie rapprochée et en macrophotographie, cette formule doit être corrigée pour tenir compte du grandissement (détails des calculs plus loin).
où :
- est le grandissement transversal (toujours négatif en photographie) ;
- est le grandissement pupillaire, rapport des diamètres des pupilles d'entrée et de sortie.
Le nombre d'ouverture par le nombre d'ouverture effectif défini par :
- .
Dans les objectifs de construction quasi-symétrique, et notamment la plupart de ceux utilisés dans les chambres photographiques[10], le grandissement pupillaire vaut 1 et l'expression de se simplifie en .
Contrôle de la profondeur de champ[modifier | modifier le code]

Le diaphragme est un élément essentiel dans la maîtrise de la prise de vue. Son réglage agit directement sur la profondeur de champ. À focale et distance de mise au point identiques, la fermeture du diaphragme augmente la profondeur de champ et contribue à la netteté de la photographie. Ceci reste vrai jusqu’à l’apparition des phénomènes de diffraction.
Les deux premières photographies montrent l'influence du diaphragme sur l'étendue de la zone de netteté. La première a été prise avec une grande ouverture, la seconde avec une petite ouverture. La vitesse d'obturation a été ajustée en conséquence mais tous les autres paramètres sont restés identiques.
-
Diaphragme ouvert
-
Diaphragme fermé
-
Objectif vu pour deux ouvertures
L’ouverture du diaphragme permet aussi de calculer la valeur l’hyperfocale : , où est la distance focale de l’objectif, le diamètre du cercle de confusion admissible, et l’ouverture.
- En faisant la mise au point sur l'infini, le premier plan net correspond à la distance hyperfocale.
- En faisant la mise au point sur la distance hyperfocale, le photographe obtient une profondeur de champ s’étalant de la moitié de cette distance à l’infini.
- Pour les autres distances de mise au point (suffisamment éloignées tout de même), l’hyperfocale est un intermédiaire de calcul permettant d'obtenir les distances du premier plan net et du dernier plan net .
Pour la macrophoto, la nature morte, etc., une grande profondeur de champ est généralement nécessaire pour bien mettre en valeur le sujet. Des zones floues sur la photo d'un insecte, par exemple, perturbent considérablement la vision. Dans le cas du portrait, au contraire, une faible profondeur de champ améliore la sensation de relief et met en valeur le sujet principal net bien détaché sur un fond flou. Le « floutage » du fond est grandement facilité si l'on prend soin d'éloigner le modèle de l'arrière-plan.
Diffraction et aberrations optiques[modifier | modifier le code]
La netteté de l'image est généralement meilleure aux ouvertures intermédiaires, celle-ci étant limitée par les aberrations géométriques à grande ouverture (N petit) et par les phénomènes de diffraction à petite ouverture (N grand).
Diffraction[modifier | modifier le code]
La diffraction n’est pas à proprement parler une aberration, elle est constitutive de la nature ondulatoire de la lumière. La lumière passant par l’ouverture du diaphragme est diffractée. Plus l’ouverture est faible, plus le phénomène sera sensible.
En photographie, la diffraction influe sur la netteté de l’image, si le diamètre de la tache produite est supérieur au cercle de confusion admissible elle devient perceptible et nuit à la netteté. Si dans un premier temps la fermeture du diaphragme compense les aberrations optiques, une ouverture trop petite générera une diffraction trop importante. L'ouverture est généralement limitée à f/16 ou f/22.
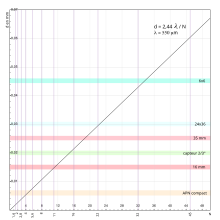
L'influence de la diffraction est plus importante avec des capteurs de petite taille, comme sur les APN compacts. En effet, le diamètre de la tache due à la diffraction est directement lié à l'ouverture du diaphragme et à la longueur d'onde de la lumière :
- .
La diffraction dépend aussi des caractéristiques des bords du diaphragme. Des bords nets, lisses et fins produiront une diffraction moindre.
-
f/5,6
-
f/8
-
f/11
-
f/16
-
f/22
-
f/32
Aberrations optiques[modifier | modifier le code]

À grande ouverture, l’objectif se retrouve hors des limites des conditions d’approximation de Gauss, et des aberrations peuvent perturber l'image.
La fermeture du diaphragme contribue à en éliminer ou en diminuer certaines sur l'image ou sur une partie de l'image formée. C’est le cas pour les aberrations de sphéricité au centre et sur les bords, de coma et le vignettage sur les bords, les aberrations chromatiques axiales et dans une moindre mesure pour l’astigmatisme. La position du diaphragme a une influence sur la distorsion.
-
Aberration sphérique
-
Coma
-
Distorsion
-
Astigmatisme
-
Aberration chromatique
-
Vignettage
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Bernard Balland, Optique géométrique : Imagerie et instruments, éd. PPUR, 2007 (ISBN 2880746892). [(fr) Aperçu de l'ouvrage sur Google Livres]
- (en) Ralph E Jacobson et al, The Manual of Photography: Photographic and Digital Imaging, Focal Press, 2000, 9e éd., 464 p. (ISBN 0240515749). [(en) Aperçu de l'ouvrage sur Google Livres]
- (en) Sidney F Ray, Applied Photographic Optics, Focal Press, 2002, 3e éd., 680 p. (ISBN 0240515404). [(en) Aperçu de l'ouvrage sur Google Livres]
Liens externes[modifier | modifier le code]
- Ouvertures et pupilles, article très détaillé de Pierre Toscani.
Notes et références[modifier | modifier le code]
- Cet article est partiellement ou en totalité issu de l'article intitulé « Diaphragme (photographie) » (voir la liste des auteurs).
- Bernard Balland, Optique géométrique : imagerie et instruments, Lausanne, Presses polytechniques et universitaires romandes, , 860 p. (ISBN 978-2-88074-689-6, lire en ligne), p. 683
- Vincent Pinel, Techniques du cinéma, Presses universitaires de France., coll. « Que sais-je ? » (no 1873), (lire en ligne)
- Robert Andréani, L'objectif photographique, Paris, De Francia, , 160 p., p. 30
- René Bouillot, Cours de photographie : technique et pratique, Paris, Dunod, , 206 p. (ISBN 2-10-000325-9), p. 28
- « Expressions : ouverture », sur Dictionnaire de français Larousse : « Ouverture relative d'un objectif, rapport du diamètre utile de l'objectif à la distance focale, exprimé sous la forme 1 : n. »
- « Définitions de OUVERTURE », sur Centre National de Ressources Textuelles et Lexicales : « Ouverture (relative d'un objectif). Rapport du diamètre du diaphragme (d'un objectif) à la distance focale (d'apr. Sarm. Phys. 1981). »
- L'arrondi conventionnel présente quelques incohérences. Par exemple, l'ouverture pour AV = 3½ (≈ 3,3636) est arrondie vers le bas à 3,3, alors que celle pour AV = 4½ (≈ 4,7568) est arrondie vers le haut à 4,8. Il y a aussi des ambigüités : la valeur 1,2 peut représenter 1,19 (AV = ½) ou 1,26 (AV = ⅔), de même que 13 peut signifier 12,7 (AV = 7½) ou 13,5 (AV = 7⅓).
- L'étalonnage des posemètres est régi par la norme ISO 2720, dérivée de ANSI PH3.49-1971. Cette dernière se base sur l'hypothèse T = 0,9, mais contient d'autres facteurs qui reviennent à adopter T = 0,83. C.f. Exposure Metering – Relating Subject Lighting to Film Exposure, par Jeff Conrad.
- (en) Ralph E. Jacobson et al, The Manual of Photography: Photographic and Digital Imaging, p. 69.
- Emmanuel Bigler, « Lumière, diaphragme et pupilles : Optiques épaisses, deuxième partie », sur galerie-photo, : « La plupart des optiques de chambre y compris les grand-angulaires à l’exception des télé-objectifs [...] sont des formules quasi-symétriques [...]. »















































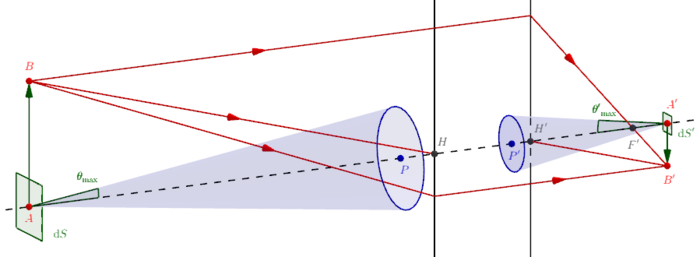



















![{\displaystyle \mathrm {d} ^{2}\Phi =L\cdot \mathrm {d} ^{2}S\cdot 2\pi \cdot \left[{\frac {\sin ^{2}\theta }{2}}\right]_{0}^{\theta _{\max }}=L\cdot \mathrm {d} ^{2}S\cdot \pi \cdot \sin ^{2}\theta _{\max }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a595635943f0fa6821257c6b6c79f3ff15643fbb)