Flux lumineux

Flux lumineux

Données clés

Unités SI	lumen (lm)
Dimension	J
Base SI	cd⋅sr
Nature	Grandeur scalaire conservative extensive
Symbole usuel	$\Phi _{\mathrm {v} }$, $\Phi$
Lien à d'autres grandeurs	$\Phi _{v}=K_{\mathrm {m} }\int _{0}^{\infty }\Phi _{\mathrm {e} ,\lambda }(\lambda )\,V(\lambda )\,\mathrm {d} \lambda .$ $\mathrm {d} \Phi _{\mathrm {v} }$ = $I_{\mathrm {v} }$ ${\mathrm {d} \Omega }$

Le flux lumineux est la grandeur photométrique qui caractérise la puissance lumineuse d'une source, telle qu'elle est perçue par l'œil humain. Le flux lumineux est le flux énergétique, c'est-à-dire la puissance électromagnétique rayonnée, pondéré par la sensibilité de l'œil humain, normalisée par la fonction d'efficacité lumineuse spectrale, aux différentes longueurs d'onde.

En effet, un rayonnement électromagnétique monochromatique produit une sensation visuelle d'intensité très variable selon la longueur d'onde, et une sensation nulle en dehors du spectre visible. Les rayonnements invisibles pour l’œil humain, tels que les infrarouges et ultraviolets, qui peuvent pourtant cumuler une puissance rayonnée considérable dans de nombreux cas, n'ont aucune influence dans le calcul ou la mesure du flux lumineux.

Il peut s'agir du flux total émis par une source – les fabricants de lampes électriques renseignent la valeur du flux total émis au côté de la puissance électrique consommée et de la température de couleur – ou du flux émis dans une portion limitée de l'espace – dans les instruments optiques, les diaphragmes, en interceptant une partie du faisceau lumineux, permettent de régler le flux reçu par un capteur ou un détecteur.

Définition

Le flux lumineux est la grandeur fondamentale en photométrie : elle permet de définir toutes les autres grandeurs photométriques.

Il est défini à partir du flux énergétique $\Phi _{\mathrm {e} }$ (exprimé en watts) plus souvent nommé puissance rayonnée. Ce dernier est un flux d'énergie rayonnée : $\Phi _{\mathrm {e} }={\frac {\mathrm {d} Q_{\mathrm {ray} }}{\mathrm {d} t}}$, où $Q_{\mathrm {ray} }$ est l'énergie rayonnée, exprimée en joules (J).

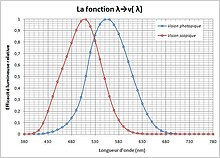
En photométrie, pour tenir compte de la sensibilité de l'œil humain, différente à chaque longueur d'onde du rayonnement, on corrige la puissance du rayonnement électromagnétique en le pondérant par une fonction d'efficacité lumineuse spectrale. Ces fonctions sont définies par des valeurs tabulées et deviennent nulles pour l'infrarouge ou l'ultraviolet qui se situent hors du domaine du spectre visible. Elles diffèrent selon le domaine de vision dans lequel on se trouve : vision diurne ou nocturne.

Vision photopique

En vision photopique (diurne) :

$\Phi _{\mathrm {v} ,\lambda }(\lambda )=\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K(\lambda )=\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K_{\mathrm {m} }\,V(\lambda )$,

où

• $K(\lambda )$ est la fonction d'efficacité lumineuse spectrale photopique ;
• $K_{\mathrm {m} }=$ 683 lm/W est l'efficacité lumineuse spectrale maximale photopique selon la définition de la candela ; elle correspond à une fréquence de 540 THz, c'est-à-dire à une longueur d'onde de très proche de 555 nm dans l'air (jaune–vert) ;
• $V(\lambda )$, aussi notée ${\overline {y}}(\lambda )$ en colorimétrie, est l'efficacité lumineuse spectrale relative photopique, sans dimension.
• $\Phi _{\mathrm {e} ,\lambda }={\frac {\mathrm {d} \Phi _{\mathrm {e} }}{\mathrm {d} \lambda }}$ est la densité spectrale de flux énergétique, en watts par mètre (W/m) ;
• $\Phi _{\mathrm {v} ,\lambda }(\lambda )$ est la densité spectrale de flux lumineux, en lumens par mètre (lm/m) ;

Pour une lumière polychromatique, le flux lumineux d' est obtenu par intégration :

$\Phi _{\mathrm {v} }=\int _{0}^{\infty }\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K(\lambda )\,\mathrm {d} \lambda =K_{\mathrm {m} }\int _{0}^{\infty }\Phi _{\mathrm {e} ,\lambda }(\lambda )\,V(\lambda )\,\mathrm {d} \lambda .$

Cette expression est souvent considéré de façon incorrecte comme l'interprétation de la loi d'Abney qui lui est proche.

Vision scotopique

En vision scotopique (nocturne), les expressions sont identiques, seule la fonction d'efficacité lumineuse spectrale utilisée est différente compte tenu du fait que seuls les bâtonnets fonctionnent :

$\Phi _{\mathrm {v} ,\lambda }(\lambda )=\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K'(\lambda )=\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K'_{\mathrm {m} }\,V'(\lambda )$,

où

• $K'(\lambda )$ est la fonction d'efficacité lumineuse spectrale scotopique ;
• $K'_{\mathrm {m} }=$ 1 700,05 lm/W^{[réf. nécessaire]} est l'efficacité lumineuse spectrale maximale scotopique, correspondant à une fréquence de 590 THz, c'est-à-dire à une longueur d'onde de 507 nm dans l'air ;
• $V'(\lambda )$ est l'efficacité lumineuse spectrale relative scotopique, sans dimension.
• $\Phi _{\mathrm {e} ,\lambda }$ est la densité spectrale de flux énergétique, en watts par mètre (W/m) ;
• $\Phi _{\mathrm {v} ,\lambda }(\lambda )$ est la densité spectrale de flux lumineux, en lumens par mètre (lm/m) ;

Par intégration sur le domaine visible, le flux lumineux pour une lumière polychromatique :

$\Phi _{\mathrm {v} }=\int _{0}^{\infty }\Phi _{\mathrm {e} ,\lambda }(\lambda )\,K'(\lambda )\,\mathrm {d} \lambda =K'_{\mathrm {m} }\int _{0}^{\infty }\Phi _{\mathrm {e} ,\lambda }(\lambda )\,V'(\lambda )\,\mathrm {d} \lambda .$

Unité

L'unité SI de flux lumineux est le lumen, symbole lm. Le nom lumen est construit sur le mot latin signifiant lumière. Il équivaut a un candela-stéradian et a pour dimension J.

Ordres de grandeur

Les efficacités lumineuses des différentes sources d'éclairage peuvent varier selon que la puissance est essentiellement émise dans la zone proche du maximum de sensibilité (cas d'une lampe fluorescente, d'une diode électroluminescente) ou essentiellement hors du visible et en particulier dans les infrarouges (cas d'une lampe à incandescence ou d'une lampe à incandescence halogène).

• Lampe halogène 70 W : Φ_v = 1 200 lm.
• Lampe éclairage urbain (sodium haute pression) 400 W : Φ_v = 28 000 lm.
• Lampe projecteur de cinéma (xénon) 2 000 W : Φ_v = 80 000 lm.

Une bougie d'intensité 1 cd émettant de façon supposée isotrope (identique dans toutes les directions) émet un flux lumineux Φ_v = 12,6 lm.

grandeurs et unités photométriques du SI

Grandeur		Unité		Dimension (hors unité SI)	Notes
Nom	Symbole	Nom	Symbole
Quantité de lumière	Qv	lumen seconde	lm⋅s	T⋅J	Le lumen seconde est parfois appelé le talbot.
Flux lumineux	Φv	lumen (candela⋅stéradian)	lm (cd⋅sr)	J	Quantité de lumière par unité de temps
Intensité lumineuse	Iv	candela (lumen par stéradian)	cd (lm/sr)	J	Flux lumineux par unité d'angle solide
Luminance	Lv	candela par mètre carré (lumen par stéradian par mètre carré)	cd/m2 (lm/sr/m2)	L−2⋅J	Flux lumineux par unité d'angle solide par unité de surface de source projetée. La candela par mètre carré est parfois appelé le nit.
Éclairement lumineux	Ev	lux (lumen par mètre carré)	lx (lm/m2)	L−2⋅J	Flux lumineux reçu sur une surface
Exitance lumineuse	Mv	lumen par mètre carré	lm/m2	L−2⋅J	Flux lumineux émis depuis une surface
Exposition lumineuse	Hv	lux seconde	lx⋅s	L−2⋅T⋅J	Éclairement lumineux intégré en fonction du temps
Densité de quantité de lumière	ωv	lumen seconde par mètre cube	lm⋅s/m3	L−3⋅T⋅J
Efficacité lumineuse (d'un rayonnement)	K	lumen par watt	lm/W	M−1⋅L−2⋅T3⋅J	Quotient du flux lumineux sur le flux énergétique
Efficacité lumineuse (d'une source)	η	lumen par watt	lm/W	M−1⋅L−2⋅T3⋅J	Quotient du flux lumineux sur la puissance consommée
Coefficient lumineux	V			1	Efficacité lumineuse normalisée par l'efficacité maximale possible
Voir aussi : SI Photométrie Radiométrie

Mesure

La mesure du flux lumineux passe par celle de l'éclairement lumineux d'une surface de référence. La découverte au XIX^e siècle de l'effet photoélectrique, a permis au XX^e siècle le développement d'appareils portables, donnant directement une mesure de l'éclairement lumineux.

Auparavant et depuis le milieu du XIX^e siècle, furent mis au point des photomètres permettant de quantifier l'éclairement, par comparaison avec une source prise comme référence. On comparait visuellement la luminance de deux écrans de même taille dont l'un est éclairé par une source étalon. Le cas de la comparaison visuelle permet d'exposer le raisonnement, sans se préoccuper de la pondération des longueurs d'onde.

Calculs simples

Intensité lumineuse et flux lumineux

La relation entre intensité lumineuse $I_{\mathrm {v} }$ en candela (cd) d'un faisceau et flux lumineux $\Phi _{\mathrm {v} }$ qui en est la cause, fréquemment utilisée pour résoudre des problèmes simples, est :

$\Phi _{\mathrm {v} }=I_{\mathrm {v} }\cdot \Omega$,

où Ω est l'angle solide, en stéradians (sr), dans lequel le flux lumineux est concentré, l'intensité lumineuse obtenue étant d'autant plus grande que l'angle solide du pinceau est étroit. Cette formule n'est valable que si l'intensité lumineuse est uniforme sur tout l'angle solide considéré.

Éclairement et flux lumineux

L'éclairement lumineux moyen $E_{\mathrm {v} \ \mathrm {moy} }$ en lux (lx) d'une surface s'exprime comme le rapport du flux reçu par l'aire $S$ :

$E_{\mathrm {v} \ \mathrm {moy} }={\frac {\Phi _{\mathrm {v} \ \mathrm {recu} }}{S}}$.

Exitance et flux lumineux

L'exitance lumineuse moyenne $M_{\mathrm {v} \ \mathrm {moy} }$ en lumens par mètre carré (lm/m²) d'une surface s'exprime comme le rapport du flux émis par l'aire $S$ :

$M_{\mathrm {v} \ \mathrm {moy} }={\frac {\Phi _{\mathrm {v} \ \mathrm {{\acute {e}}mis} }}{S}}$.

Grandeurs et unités photométriques et radiométriques

Le tableau ci-dessous rassemble les grandeurs, symboles, unités et dimensions des grandeurs énergétiques ou radiométriques, ainsi que des grandeurs lumineuses ou photométriques qui leur sont associées selon la norme ISO 80000-7.

Grandeurs et unités radiométriques et photométriques

Grandeur radiométrique	Symbole	Unité SI (symbole)	Dimension	Grandeur photométrique	Symbole	Unité SI (symbole)	Dimension
Énergie rayonnée	$Q_{e}$	joule (J)	M L2 T−2	Quantité de lumière	$Q_{v}$	lumen seconde (lm s)	J Ω T
Flux énergétique (puissance rayonnée)	$\phi _{e}$	watt (W)	M L2 T−3	Flux lumineux	$\phi _{v}$	lumen (lm)	J Ω
Intensité énergétique	$I_{e}$	watt par stéradian (W sr−1)	M L2 T−3 Ω−1	Intensité lumineuse	$I_{v}$	candela (cd)	J
Luminance énergétique / Radiance	$L_{e}$	watt par mètre carré et par stéradian (W m−2 sr−1)	M T−3 Ω−1	Luminance lumineuse / Luminance	$L_{v}$	candela par mètre carré (cd m−2)	J L-2
Éclairement énergétique / Irradiation / Irradiance	$E_{e}$	watt par mètre carré (W m−2)	M T−3	Éclairement lumineux	$E_{v}$	lux (lx)	J Ω L-2
Exitance / Émittance énergétique	$M_{e}$	watt par mètre carré (W m−2)	M T−3	Exitance / Émittance lumineuse	$M_{v}$	lux (lx)	J Ω L-2
Exposition énergétique	$H_{e}$	joule par mètre carré (J m−2)	M T-2	Exposition lumineuse / Lumination	$H_{v}$	lux seconde (lx s)	J Ω T L-2

Le tableau ci-dessous présente les relations entre les grandeurs radiométriques et les grandeurs photométriques.

Relation entre les grandeurs radiométriques et les grandeurs photométriques

Grandeur	Symbole	Unité SI (symbole)	Dimension	Description
Efficacité lumineuse (d'un rayonnement)	K	lumen par watt (lm W−1)	JΩM−1L−2T3	Quotient du flux lumineux sur le flux énergétique
Efficacité lumineuse (d'une source)	η	lumen par watt (lm W−1)	JΩM−1L−2T3	Quotient du flux lumineux sur la puissance consommée
Coefficient lumineux	V		1	Efficacité lumineuse normalisée par l'efficacité maximale possible

Annexes

Articles connexes

• Flux énergétique
• Efficacité lumineuse 
• Efficacité lumineuse spectrale
• Bougie (unité)

Bibliographie

• André Moussa et Paul Ponsonnet, « XVIII — Éléments de photométrie », dans Cours de physique — Optique, Lyon, Desvigne, 1988, p. 239-245.
• Robert Sève, Science de la couleur : aspects physiques et perceptifs, Marseille, Chalagam, 2009, 374 p. (ISBN 978-2-9519607-5-6 et 2-9519607-5-1).
• Jean Terrien et François Desvignes, La photométrie, Paris, PUF, coll. « Que-Sais-Je » (n^o 1167), 1972, 1^re éd., 128 p. (présentation en ligne).
• (en) Michael Bass, Casimer DeCusatis, Jay Enoch et Vasudevan Lakshminarayanan, Handbook of Optics, Volume II : Design, Fabrication and Testing, Sources and Detectors, Radiometry and Photometry, McGraw Hill Professional, 6 octobre 2009, 3^e éd., 1264 p. (ISBN 978-0-07-162927-0, présentation en ligne).