Théorème de Viviani

Le théorème de Viviani est un théorème de géométrie euclidienne portant sur le triangle équilatéral. Il porte le nom du mathématicien italien Vincenzo Viviani qui l'a publié en 1649.

Énoncé[modifier | modifier le code]

Théorème de Viviani — Dans un triangle équilatéral, la somme des distances d'un point intérieur au triangle aux trois côtés est égale à la hauteur du triangle.

Démonstration[modifier | modifier le code]

Soient $(\mathrm {ABC} )$ un triangle équilatéral de côté $a$ et P un point intérieur à ce triangle. On note $h$ la longueur commune des hauteurs du triangle, et l, m et n les distances de P aux côtés du triangle, respectivement [AB], [AC] et [BC].

On note ${\mathcal {A}}(\mathrm {ABC} )$ l'aire du triangle $(\mathrm {ABC} )$ . Par construction :

{\mathcal {A}}(\mathrm {ABC} )={\mathcal {A}}(\mathrm {ABP} )+{\mathcal {A}}(\mathrm {ACP} )+{\mathcal {A}}(\mathrm {BCP} )

,

c'est-à-dire :

{\frac {ah}{2}}={\frac {al}{2}}+{\frac {am}{2}}+{\frac {an}{2}}

donc

l+m+n=h

.

Réciproque[modifier | modifier le code]

Si la somme des distances aux côtés d'un point intérieur à un triangle est constante, alors ce triangle est équilatéral ^[1].

Plus précisément, pour un triangle non isocèle la somme des distances aux côtés possède un minimum strict au sommet dont est issu la plus petite hauteur (donc dont le côté opposé est le plus grand)^[2].

Pour un triangle isocèle dont l'angle au sommet est strictement supérieur à 60°, le minimum est atteint au sommet, et pour un triangle isocèle dont l'angle au sommet est strictement inférieur à 60°, le minimum est atteint en tout point de la base^[2].

Généralisations[modifier | modifier le code]

Dans cet heptagone régulier, la somme des hauteurs PI + PJ + PK + PL + PM + PN + PO est indépendante de la position de P.

Polygones réguliers[modifier | modifier le code]

Dans son édition du cinquième livre des Coniques d'Apollonius^[3], Viviani démontre un résultat plus général :

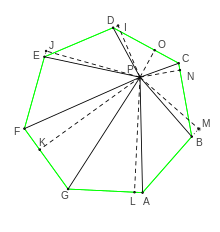
Généralisation — Dans un polygone régulier convexe, la somme des distances d'un point intérieur au polygone aux côtés^[4] du polygone est indépendante de la position du point.

Cette propriété utilise le même argument que précédemment. Si P est à l'intérieur du polygone A₁...A_n, les segments PA₁, ...PA_n découpent le polygone en n triangles de bases A₁A₂, A₂A₃, ..., A_nA₁. L'aire du polygone est alors égale à la somme des aires de chaque triangle. Les triangles ayant des bases de même taille (la taille d'un côté), la somme des aires est égale au produit de la somme des hauteurs par un demi-côté. L'aire du polygone et la longueur d'un demi côté étant indépendants de P, la somme des hauteurs est aussi indépendante de P. On peut évaluer alors cette somme à n fois l'apothème (la distance séparant le centre du polygone d'un côté).

Viviani démontre en outre que si le point P est extérieur au polygone, la somme des distances de P aux côtés du polygone est toujours strictement supérieure à la somme précédente. En effet, dans ce cas, les triangles de bases A₁A₂, A₂A₃, ..., A_nA₁ et de sommet P recouvrent le polygone par excès, la somme de leurs aires est strictement supérieure à celle du polygone et la somme des hauteurs est strictement supérieure à n fois la distance entre le centre et un côté.

Autres polygones convexes[modifier | modifier le code]

La généralisation ci-dessus s'étend même aux polygones convexes équiangles (comme les rectangles) ainsi qu'à ceux qui sont équilatéraux (comme les losanges) ou dont les côtés sont en nombre pair et parallèles par paires de côtés opposés (comme les parallélogrammes)^[5].

Une condition nécessaire et suffisante pour qu'un polygone convexe possède la propriété de constance de la somme des distances aux côtés est que cette propriété soit vraie pour trois points non alignés internes au triangle^[5].

Polyèdres convexes[modifier | modifier le code]

La somme des distances aux faces d'un point intérieur d'un polyèdre convexe est constante si le polyèdre a toutes ses faces de même aire (donc en particulier pour un polyèdre régulier), par un argument de volume similaire à celui des aires pour le cas plan^[5].

Par exemple, tous les tétraèdres ayant des faces de même aire (i.e. équifaciaux) possèdent la propriété, et non seulement le tétraèdre régulier^[1].

La somme est également constante pour les polyèdres dont les faces sont en nombre pair et parallèles par paires de faces opposées (comme les parallélépipèdes et les polyèdres d'Archimède, sauf les deux adoucis).

Notes et références[modifier | modifier le code]

↑ ^{a et b} (en) Chen, Zhibo; Liang, Tian, « The converse of Viviani's theorem », The College Mathematics Journal. 37 (5):,‎ 2006, p. 390–391 (lire en ligne)
↑ ^{a et b} Jean-Baptiste Hiriart-Urruty, « La géométrie du triangle et l'optimisation convexe font bon ménage... », Université Paul Sabatier,‎ 20??, p. 6 (lire en ligne)
↑ (la) Apolonio de Pérgamo, Vincenzo Viviani, De maximis et minimis geometrica…, 1659, Appendice, p. 146 sur Google Livres.
↑ Éventuellement prolongés hors du polygone.
↑ ^{a b et c} (en) Abboud, Elias, « On Viviani's Theorem and its Extensions », College Mathematics Journal. 43 (3),‎ 2010, p. 203–211 (lire en ligne)

Voir aussi[modifier | modifier le code]

Liens externes[modifier | modifier le code]

(en) « Viviani's Theorem: What is it? », sur Cut The Knot

[:0-1] {a et b} (en) Chen, Zhibo; Liang, Tian, « The converse of Viviani's theorem », The College Mathematics Journal. 37 (5):,‎ 2006, p. 390–391 (lire en ligne)

[:2-2] {a et b} Jean-Baptiste Hiriart-Urruty, « La géométrie du triangle et l'optimisation convexe font bon ménage... », Université Paul Sabatier,‎ 20??, p. 6 (lire en ligne)

[3] (la) Apolonio de Pérgamo, Vincenzo Viviani, De maximis et minimis geometrica…, 1659, Appendice, p. 146 sur Google Livres.

[4] Éventuellement prolongés hors du polygone.

[:1-5] {a b et c} (en) Abboud, Elias, « On Viviani's Theorem and its Extensions », College Mathematics Journal. 43 (3),‎ 2010, p. 203–211 (lire en ligne)

[1]

[2]

[3]

[4]

[5]

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron