Tétraèdre
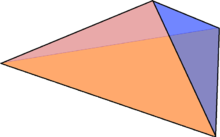

En géométrie, les tétraèdres (du grec tétra : quatre) sont des polyèdres de la famille des pyramides, composés de 4 faces triangulaires, 6 arêtes et 4 sommets [1],[2].
Propriétés combinatoires[modifier | modifier le code]
Le 3-simplexe est la représentation abstraite du tétraèdre ; dans ce modèle, les arêtes s'identifient aux 6 sous-ensembles à 2 éléments de l'ensemble des quatre sommets, et les faces aux 4 sous-ensembles à 3 éléments.
Chaque sommet d'un tétraèdre est relié à tous les autres par une arête, et de même chaque face est reliée à toutes les autres par une arête. Ces caractéristiques sont rares : seulement deux polyèdres possédant la première propriété ont été découverts : le tétraèdre et le polyèdre de Császár, qui a 7 sommets d'ordre 6, 14 faces triangulaires et 21 arêtes ; de même, seulement deux polyèdres possédant la seconde propriété ont été découverts, le tétraèdre et le polyèdre de Szilassi, qui a 14 sommets, 7 faces hexagonales et 21 arêtes ; les polyèdres de Császár et de Szilassi sont duaux et sont homéomorphes au tore.
Le 1-squelette d'un tétraèdre — l'ensemble de ses sommets reliés par ses arêtes — forme un graphe complet appelé graphe tétraédrique et noté .
Points remarquables[modifier | modifier le code]
Beaucoup de points remarquables du triangle ont des analogues pour le tétraèdre, à l'exception notable de l'orthocentre. C'est en particulier le cas du centre de la sphère circonscrite (intersection des plans médiateurs des arêtes), des centres des sphères inscrites et exinscrites (intersections des plans bissecteurs), ou du centre de gravité. Un tétraèdre est dit « orthocentrique » lorsque ses quatre hauteurs sont concourantes ; le point de concours est alors l'orthocentre du tétraèdre. Une généralisation de l'orthocentre, qui coïncide avec lui pour les tétraèdres orthocentriques mais qui est toujours définie, est le point de Monge, intersection des plans orthogonaux à une arête et passant par le milieu de l'arête opposée[3],[4].
Propriétés métriques[modifier | modifier le code]
Construction[modifier | modifier le code]
La donnée des 6 longueurs des arêtes permet la construction du tétraèdre si et seulement si ces longueurs vérifient (strictement) l'inégalité triangulaire. Si on précise l'ordre des arêtes, il n'y a (à isométrie près) que deux solutions, images miroir l'une de l'autre ; une réalisation concrète (à l'aide de barres rigides, par exemple) est nécessairement sans aucun degré de liberté, et donc non déformable.
Tétraèdre de Héron[modifier | modifier le code]
Un tétraèdre dont toutes les arêtes, toutes les aires des faces, et le volume sont des nombres entiers est appelé un tétraèdre de Héron ; c'est par exemple le cas du tétraèdre ayant pour arêtes 896, 990 (pour l'arête opposée) et 1073 (pour les quatre autres)[5].

Volume du tétraèdre[modifier | modifier le code]
Comme pour toute pyramide, la formule de calcul du volume d'un tétraèdre quelconque est :
où S est l'aire d'une base du tétraèdre et h la hauteur du tétraèdre s'appuyant sur cette base.
Pour un tétraèdre construit sur A, B, C et D,
où est le produit mixte de .
Une généralisation de la formule de Héron utilisant le déterminant de Cayley-Menger donne le volume à partir des longueurs des six côtés
Soit

où sont les longueurs des côtés d'une face, et les couples de longueurs d'arêtes opposées [6]. Elle a été obtenue sous sa forme développée par Piero della Francesca [7].
Si sont les longueurs des arêtes issues d'un même sommet, et les mesures des angles des faces arrivant à ce sommet, on a la formule, obtenue en 1752 par Euler[8],[9] :
,
soit
où [6].
Distances entre les arêtes[modifier | modifier le code]
On peut calculer la distance entre deux arêtes opposées d'un tétraèdre ABCD, par exemple (AB) et (CD) ayant un angle , en appliquant la formule de la distance entre deux droites gauches : où , soit .
On en déduit la formule du volume :
où sont les longueurs de deux arêtes opposées, leur distance et leur angle.
Angles[modifier | modifier le code]
Outre les 12 angles des quatre faces (calculables par les formules classique de trigonométrie du triangle), il y a 6 angles dièdres correspondant aux six arêtes, et 4 angles solides correspondants aux quatre sommets. Notant (P1, P2, P3, P4) les quatre sommets d'un tétraèdre, on notera θij l'angle dièdre entre les deux faces adjacentes à l'arête (PiPj), Ωi l'angle solide en Pi et Δi l'aire de la face opposée au sommet Pi.
Les outils du calcul vectoriel (produit scalaire et produit vectoriel) permettent un calcul facile de ces angles ; on a par exemple orthogonal à la face (ABC), et donc en posant et , on voit que . La formule de Girard donne alors très simplement l'angle solide : .
De très nombreuses formules de trigonométrie du triangle se généralisent au tétraèdre (on en trouvera certaines dans l'article trigonométrie sphérique, et un ensemble complet dans l'article trigonométrie du tétraèdre) ; on a par exemple une « loi des cosinus » (analogue au résultat de ce nom pour les triangles) reliant les aires des faces aux angles dièdres[10] :
- .
Il existe par ailleurs une relation entre les angles dièdres liée au déterminant de Cayley-Menger[11] :
- .
Tétraèdres remarquables[modifier | modifier le code]

Tétraèdre régulier[modifier | modifier le code]
Le tétraèdre régulier est l'un des cinq solides de Platon.
Tous les points remarquables usuels du tétraèdre régulier sont confondus en un point unique, appelé centre du tétraèdre (bien que ce ne soit pas un centre de symétrie).
Pour un tétraèdre régulier inscrit dans une sphère de rayon r :
Arête .
Rayon h de la sphère inscrite dans le tétraèdre = .
Tétraèdre orthocentrique[modifier | modifier le code]
Tétraèdre équifacial[modifier | modifier le code]
Tétraèdre trirectangle[modifier | modifier le code]

Tétraèdre quadrirectangle[modifier | modifier le code]

Un tétraèdre est dit quadrirectangle lorsque les quatre faces sont des triangles rectangles. Les quatre angles droits se répartissent alors forcément entre deux sommets, deux angles droits dans chacun, d'où l'autre appellation de bicoin [12].
Avec les notations du patron ci-contre, les longueurs a,b,c,x, étant choisies, les longueurs y,z sont obtenues par les relations .
Le tétraèdre quadrirectangle peut être construit à partir d'un pavé droit en prenant les quatre sommets de trois arêtes consécutives non coplanaires, et le pavé est réunion quasi-disjointe de six tétraèdres de ce type. Ceci montre que le tétraèdre quadrirectangle pave l'espace.
Lorsque a = b = x, autrement dit lorsque le pavé précédent est un cube, le tétraèdre quadrirectangle est dit équilatéral [12], et c'est un cas particulier de tétraèdre de Hill. On a alors .
Tétraèdres de Möbius[modifier | modifier le code]

La configuration de Möbius est formée de deux tétraèdres dont chacun est « inscrit » dans l'autre (il n'en existe pas d'équivalent pour les triangles) : on peut construire deux tétraèdres dits tétraèdres de Möbius tels que les sommets de chacun d'entre eux appartiennent aux plans (respectifs) des faces opposées de l'autre. La figure jointe en montre un exemple.
Fortifications et Mur de l'Atlantique[modifier | modifier le code]
Des tétraèdres en béton ou en acier, de diverses dimensions sont utilisés pendant la Seconde Guerre mondiale comme obstacles antichars par les divers belligérants et pour s'opposer au débarquement de péniches de débarquement et chars alliés en cas de tentative de débarquement sur les plages défendues par le Mur de l'Atlantique.
-
Tétraèdres en béton sur la plage de Pen-Bron, à La Turballe.
Notes et références[modifier | modifier le code]
- Victor Thébault, Parmi les belles figures de la géométrie dans l'espace (géométrie du tétraèdre), Vuibert, (lire en ligne)
- Paul Couderc, Augustin Balliccioni, Premier livre du tétraèdre à l'usage des élèves de première, de mathématiques, et des candidats aux grandes écoles et à l'agrégation, Gauthier-Villars, , 204 p. (lire en ligne)
- Gaspard Monge, Géométrie descriptive.
- Point de Monge d'un tétraèdre.
- (en) « Problème 930 », Crux Mathematicorum, vol. 11, no 5, , p. 162–166 (lire en ligne)
- (en) W. Kahan, « What has the Volume of a Tetrahedron to do with Computer Programming Languages ? »
- (en) "Simplex Volumes and the Cayley-Menger Determinant", MathPages.com
- (la) L. Euler, Novi commentarii Academiae Scientiarum Imperialis Petropolitanae., t. IV, (lire en ligne), p. 160
- Yvonne et René Sortais, Géométrie de l'espace et du plan, Hermann, , p. 245-246
- (en) Jung Rye Lee, « The Law of Cosines in a Tetrahedron », J. Korea Soc. Math. Educ. Ser. B: Pure Appl. Math.,
- Daniel Audet, « Déterminants sphérique et hyperbolique de Cayley-Menger », Bulletin AMQ,
- « Le bicoin, ou tétraèdre quadrirectangle »
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Tétraèdre trirectangle
- Tétraèdre orthocentrique
- Tétraèdre équifacial
- Sphère circonscrite à un tétraèdre
- Nombre tétraédrique
Liens externes[modifier | modifier le code]
- (en) Eric W. Weisstein, « Tetrahedron », sur MathWorld













































