Octaèdre régulier

Vues  de  face,   de  profil,   et  de  dessus.
Une  arête  projetée  peut  se  réduire  à  un  point,   ou  être  cachée
par une ou deux autres arêtes.  Sinon une arête cachée est en pointillé.
Tracée  en  bleu,   la  section  équatoriale  horizontale  reproduit  à  l’échelle   √3/2   le  contour  hexagonal  régulier  de  l’octaèdre,
vu  de  dessus.

L’octaèdre régulier est le solide de Platon associé à l’air dans l’Antiquité gréco‑romaine.

Le préfixe octa indique le nombre de faces d’un octaèdre :  huit faces.  Le suffixe èdre signifie face plane.  Les faces d’un octaèdre régulier sont des triangles équilatéraux,  huit polygones réguliers qui sont isométriques.  Ses douze arêtes égales sont les côtés de trois carrés concentriques,  dans trois plans deux à deux sécants à angle droit selon une diagonale,  à la fois diagonale des deux carrés et diagonale du solide.  Le centre commun des carrés est à la fois le centre de symétrie de l’octaèdre,  son centre de gravité,  et le centre de ses sphères circonscrite et inscrite.

Un octaèdre régulier est convexe.  Son symbole de Schläfli est {3, 4},  car il a trois sommets par face,  et quatre faces par sommet.

Grandeurs caractéristiques

Octaèdre

Éléments

Faces	Arêtes	Sommets
8 triangles équilatéraux	12	6 de degré 4

Données clés

Type	Polyèdre régulier
Références d'indexation	U05 – C17 – W002
Symbole de Schläfli	{3,4}
Symbole de Wythoff	4|2 3
Diagramme C-D
Caractéristique	2
Propriétés	Deltaèdre convexe
Volume (arête a)	${1 \over 3}\,{\sqrt {2}}\;a^{3}$
Aire de surface	$2\;{\sqrt {3}}\;a^{2}$
Angle dièdre	$2\,\arctan {\sqrt {2}}\;\approx 109{,}47^{\,\circ }$
Groupe de symétrie	Oh
Dual	Cube

Si  a  est la longueur d’une arête :

• la distance entre 2 sommets opposés est $\quad a\,{\sqrt {2}}\;;$
• le rayon de sa sphère circonscrite est $\quad R={\frac {a\,{\sqrt {2}}}{2}}\;;$
• son angle dièdre est $\quad \arccos \left(-{\frac {1}{3}}\right)\approx 109{,}47^{\,\circ }\;;$
• le rayon de sa sphère inscrite est $\quad r={\frac {a\,{\sqrt {6}}}{6}}\;;$
• son aire est $\quad 2\,{\sqrt {3}}\cdot a^{2}\;;$
• son volume est $\quad {\frac {\sqrt {2}}{3}}\;a^{3}\;;$
• les 6 points de coordonnées $\;(\pm {\frac {a}{\sqrt {2}}},0,0)$, $(0,\pm {\frac {a}{\sqrt {2}}},0)\;$ et $\;(0,0,\pm {\frac {a}{\sqrt {2}}})\;$ sont les sommets d’un octaèdre régulier centré sur l’origine du repère cartésien.

Travail manuel

Un  patron  d’octaèdre  régulier

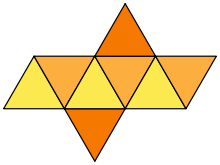
À partir d’un patron,  muni de pattes d’assemblage,  construire un octaèdre est beaucoup plus laborieux et plus coûteux en feuille à plier,  papier ou bristol,  qu’à partir de trois pièces carrées à évider,  découper,  puis imbriquer.

Un petit théâtre de géométrie 3D serait plus ambitieux qu’un octaèdre seul.  Dessinée sur scène,  la position de la structure des carrés correspondrait au décor vertical :  une projection en “élévation” des carrés encastrés,  la “ligne de terre” étant le pli horizontal du bristol le long du mur décoré.

Une succession de projets pourrait se constituer au fil des ans,  où s’imbriqueraient les quatre hexagones d’un cuboctaèdre,  puis les six décagones d’un icosidodécaèdre.  Une notice rappellerait notamment le principe de numérotation des pièces détachées,  par leurs nombres de paires d’encoches externes.  Mais avant d’envisager des dessins en SVG de pièces décagonales régulières,  plus compliquées et plus nombreuses,  l’idée des quatre hexagones imbriqués les uns dans les autres pourrait s’allier à celle des trois carrés,  ou même une seule section hexagonale de l’octaèdre.  Et des arcs de grands cercles de la sphère circonscrite pourraient embellir l’ensemble.  Par exemple,  deux séries de numérotations des pièces seraient  c_0,  c_1  et  c_2,  puis  h0…  Chaque pièce carrée  c_X  aurait un seul bord rectiligne,  de façon à poser horizontalement la structure sur une face triangulaire,  tandis que ses trois autres côtés deviendraient trois quarts du cercle circonscrit au carré initial.  S’il s’agit de traduire en 3D la toute première image de l’article,  en lui ajoutant la sphère circonscrite,  alors la section hexagonale horizontale,  ou la pièce hexagonale  h0  deviendrait une couronne ou un disque,  selon qu’elle est évidée ou non.  Dernière pièce à s’introduire dans la structure,  ses trois paires d’encoches,  toutes externes,  correspondraient chacune à une paire d’encoches internes d’une pièce  c_X,  portée par une médiatrice commune à deux côtés opposés de son carré initial :  deux côtés parallèles,  qui seraient obliques dans la structure achevée,  peut‑être tracés sur chaque pièce  c_X  aux trois quarts circulaires.

Chaque pièce détachée carrée possède un centre de symétrie,  futur centre de la structure démontable.  L’ordre croissant des numéros des pièces est leur ordre d’assemblage,  la pièce n ^o 0  accueillant d’abord la pièce 1.  Si la feuille est assez souple,  ou les évidements suffisamment grands,  ne pas évider la dernière pièce permet de marquer son centre d’une croix,  percée éventuellement d’un petit trou pour y passer un ruban,  et suspendre la structure démontable.

Plus tard nous pourrions prolonger par des triangles les pièces carrées,  dont les douze bords extérieurs deviendraient alors des plis,  ce qui rendrait la structure plus rigide.  Les triangles seraient alors prolongés par des pattes d’assemblage,  et la structure tétraèdrique laisserait voir par ses triangles évidés ses trois sections carrées.

Structure  démontable  de  trois  pièces  carrées.
Chaque encoche laisse passer largement l’épaisseur d’une autre pièce.

Étoilement et dualité

Cube  et  octaèdre  régulier  sont  duaux
l’un  de  l’autre.   Trois  polyèdres  réguliers  partagent
les  trois  sections  carrées :   les  deux  tétraèdres,
qui  ont  chacun  quatre  sommets  du  cube,
et  l’octaèdre  leur  intersection.

À partir d’un cube,  on peut construire un octaèdre régulier son dual,  en plaçant ses sommets aux centres des six faces du cube.  Cela revient à tronquer le cube par huit plans,  passant chacun par les trois sommets les plus proches du sommet éliminé.  Inversement l’étoilement d’un octaèdre régulier :  une paire de tétraèdres réguliers symétriques l’un de l’autre par rapport au centre de l’octaèdre,  a pour enveloppe convexe un cube.

Exemples

Dans les jeux

L'octaèdre régulier est utilisé comme dé à jouer, particulièrement dans les jeux de rôle.

En cristallographie

Certains cristaux comme la fluorine forment un octaèdre régulier.

En chimie

Certaines molécules peuvent avoir une géométrie moléculaire octaédrique.

Généralisation

L'hyperoctaèdre, ou n-octaèdre, est la généralisation de l'octaèdre en n dimensions.

L'hyperoctaèdre est, avec son dual l'hypercube et le n-simplexe, un des trois seuls polytopes existant sous forme régulière dans toute dimension n. Les polytopes réguliers sont en effet une infinité en dimension 2 (voir polygone régulier), 5 en dimension 3 (voir solide de Platon), 6 en dimension 4, et après ils ne sont plus que 3, comme Ludwig Schläfli l'a démontré.

Le symbole de Schläfli d'un n-octaèdre est de la forme {3, 3, 3, … , 3, 4} avec n – 1 chiffres.

Les coordonnées des sommets d'un hyperoctaèdre centré à l'origine sont obtenues en permutant les coordonnées (±1, 0, 0, … , 0, 0).

Les premiers hyperoctaèdres

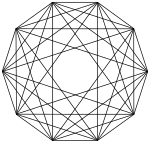
Hyperoctaèdre	Carré	Octaèdre	Hexadécachore ou 16-cellules	5-octaèdre
Dimension	2	3	4	5
Sommets	4	6	8	10
Représentation

Hypervolume d'un hyperoctaèdre régulier

L'hypervolume d'un polytope est le contenu n-dimensionnel de ce polytope. Soit a son arête.

Pour construire un (n + 1)-octaèdre, on relie les 2n sommets d'un n-octaèdre à un nouveau point au-dessus et à un nouveau point au-dessous.

• Ainsi, un segment dont les extrémités sont reliées à un point au-dessus et à un point au-dessous donne un carré (on supposera que les points ont été placés de sorte à donner un hyperoctaèdre régulier).
• Un carré dont les sommets sont reliés à un point au-dessus et à un point au-dessous donne un octaèdre.
• Un octaèdre dont les sommets sont reliés à un point au-dessus et à un point en dessous (situés dans une autre dimension) donne bien un hexadécachore.

L'hyperoctaèdre est donc une double hyperpyramide (à base hyperoctaédrique de dimension inférieure). Étant régulier dans le cas étudié, ses sommets sont tous sur une n-sphère circonscrite. Cette n-sphère circonscrite est également celle de ses faces hyperoctaédriques de dimensions inférieures, car tous les sommets de l'hyperoctaèdre régulier sont dessus. Le rayon du centre de cette n-sphère aux sommets est donc le même pour toute dimension n : $R_{n}={\frac {a{\sqrt {2}}}{2}}$.

L'hypervolume est celui de deux hyper-pyramides de hauteur $R_{n}$. On en déduit donc que l'hypervolume (le n-contenu) d'un n-octaèdre régulier d'arête a vaut :

$V_{n}={\frac {V_{n-1}\times R_{n}}{n}}\times 2={\frac {(a{\sqrt {2}})^{n}}{n!}}$.

Exemples :

• Aire du carré : $V_{2}={\frac {(a{\sqrt {2}})^{2}}{1\times 2}}=a^{2}$
• Volume de l'octaèdre régulier : $V_{3}={\frac {(a{\sqrt {2}})^{3}}{1\times 2\times 3}}={\frac {a^{3}{\sqrt {2}}}{3}}$ ;
• Hypervolume de l'hexadécachore : $V_{4}={\frac {(a{\sqrt {2}})^{4}}{1\times 2\times 3\times 4}}={\frac {a^{4}}{6}}$ ;
• …

(On suppose dans cette formule que le seul n-octaèdre à ne pas avoir une longueur d'arête égale à a est le segment (1-octaèdre), qui a dans ce cas pour longueur $a{\sqrt {2}}$ (diagonale d'un carré) pour donner bien un carré de côté a avec la méthode de construction donnée)

Notes et références

• Cet article est partiellement ou en totalité issu de l'article intitulé « Octaèdre » (voir la liste des auteurs).