Théorème de Pythagore
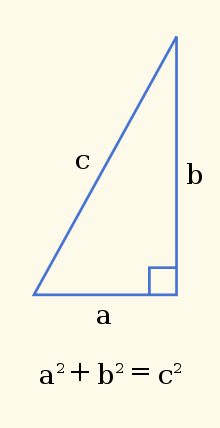
Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle. Il s'énonce fréquemment sous la forme suivante :
- Si un triangle est rectangle, le carré de la longueur de l’hypoténuse (ou côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés.
Ce théorème permet notamment de calculer l’une des longueurs à partir des deux autres.
Il doit son nom à Pythagore de Samos, philosophe de la Grèce antique du VIe siècle av. J.-C., cependant le résultat était connu plus de mille ans auparavant en Mésopotamie et a vraisemblablement été découvert indépendamment dans plusieurs autres cultures.
La plus ancienne démonstration qui nous soit parvenue est due à Euclide, vers -300. Même si les mathématiciens grecs en connaissaient sûrement une auparavant, rien ne permet de l'attribuer de façon certaine à Pythagore.
Les premières démonstrations historiques reposent en général sur des méthodes de calcul d’aire par découpage et déplacement de figures géométriques. Inversement, la conception moderne de la géométrie euclidienne est fondée sur une notion de distance qui est définie pour respecter ce théorème.
Divers autres énoncés généralisent le théorème à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère.
Plus généralement, ce théorème a de nombreuses applications dans divers domaines très différents (architecture, ingénierie...), encore aujourd'hui, et a permis nombres d'avancées technologiques à travers l'histoire.
Énoncés
Théorème

La forme la plus connue du théorème de Pythagore est la suivante :
Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. |
En particulier, la longueur de l’hypoténuse est donc toujours supérieure à celle de chaque autre côté.
Le terme « longueur » est parfois omis, chaque côté étant assimilé à sa longueur. Toutefois l’élévation au carré (algébrique), qui n’a de sens que pour une grandeur numérique comme la longueur, correspond à la construction d’un carré (géométrique) sur chaque côté du triangle. Certaines démonstrations du théorème s’appuient d’ailleurs sur une égalité d’aires entre le carré construit sur l’hypoténuse et la réunion des carrés construits sur les deux autres côtés.
En nommant les sommets du triangle, le théorème peut se reformuler dans l’implication suivante :
Théorème de Pythagore — Si un triangle ABC est rectangle en C, alors AB2 = AC2 + BC2. Avec les notations usuelles AB = c, AC = b et BC = a (cf. figure ci-dessous), la formule s’écrit encore : a2 + b2 = c2, on peut alors isoler c en appliquant l'opération de la racine carrée à l'égalité pour écrire: c = √a2 + b2  |
Par contraposée :
Théorème — Si AB2 n’est pas égal à AC2 + BC2 alors le triangle n’est pas rectangle en C. |
Réciproque
L’implication réciproque est également vraie :
Réciproque du théorème de Pythagore — Si AB2 = AC2 + BC2 alors le triangle ABC est rectangle en C.
Pour une formulation sans notations des sommets, le terme « hypoténuse » n'est utilisable qu'une fois acquis que le triangle est rectangle :
Réciproque du théorème de Pythagore — Si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et son hypoténuse est le plus grand côté.
Par contraposée de la réciproque :
Théorème — Si un triangle ABC n’est pas rectangle en C, alors AB2 n’est pas égal à AC2 + BC2.
La réciproque se déduit du théorème lui-même et d'un cas d'« égalité » des triangles : si l'on construit un triangle rectangle en C de sommets A, C et B', avec CB' = CB, on a AB = AB' par le théorème de Pythagore, donc un triangle isométrique au triangle initial (les trois côtés sont deux à deux de même longueur). L'angle en C du triangle initial ABC, identique à celui du triangle AB'C, est donc droit.
Équivalence
Comme la réciproque est vraie, on dit que l'on a une équivalence : la propriété sur les carrés des longueurs des côtés du triangle est une condition nécessaire et suffisante pour qu'il soit dit rectangle en C :
Théorème — ABC est rectangle en C si et seulement si AB2 = AC2 + BC2.
Triplets pythagoriciens
Quand trois nombres entiers vérifient la même relation que celle donnée par le théorème de Pythagore pour les côtés d'un triangle rectangle, c'est-à-dire que le carré du plus grand est la somme des carrés des deux autres, on les nomme « triplets pythagoriciens ». Le plus simple et le plus connu est le triplet (3,4,5) : 32 + 42 = 52. D'après la réciproque du théorème de Pythagore, un triangle dont les longueurs des côtés sont 3, 4 et 5 est rectangle.
Applications
Arpentage

D’après la réciproque du théorème de Pythagore, si un triangle a des côtés de longueurs 3, 4 et 5 (par rapport à une unité quelconque) alors il est rectangle.
Ce cas particulier de triplet pythagoricien justifie l’usage de la corde à treize nœuds, qui permettait de mesurer des distances mais aussi d’obtenir un angle droit sans équerre rigide en répartissant les douze intervalles qui séparent les nœuds sur les trois côtés d’un triangle de dimensions 3 – 4 – 5.
Nature d'un triangle
Le théorème (ou plutôt sa contraposée) et sa réciproque montrent que la relation donnée entre les longueurs des côtés est une propriété caractéristique des triangles rectangles, ce qui permet de l’utiliser comme test dans la détermination de la nature d’un triangle :
- si AB2 = AC2 + BC2 alors le triangle est rectangle en C ;
- si AB2 n’est pas égal à AC2 + BC2 alors le triangle n’est pas rectangle en C.
En effectuant le test pour le sommet opposé au plus grand côté du triangle (seul sommet susceptible d'abriter l'angle droit), on peut déterminer si le triangle est rectangle ou non à partir des longueurs de ses côtés.
Distance euclidienne
Dans le plan muni d’un repère orthonormé, la distance entre deux points s’exprime en fonction de leurs coordonnées cartésiennes à l’aide du théorème de Pythagore par :
.
Cette formule est analogue à celle qui donne la norme d’un vecteur de coordonnées (x ; y) dans une base orthonormée : .
Ces formules se généralisent en dimension plus grande.
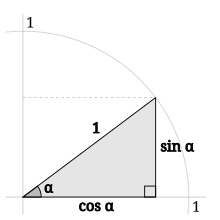
Relation trigonométrique
En considérant le cosinus et le sinus d’un angle α comme l'abscisse et l'ordonnée d’un point du cercle trigonométrique repéré par cet angle, et le rayon du cercle trigonométrique de longueur 1 comme l'hypoténuse, le théorème de Pythagore permet d’écrire :
Histoire

Pythagore vivait au VIe siècle av. J.-C., mais l'histoire du théorème de Pythagore commence plus d'un millénaire auparavant, comme en témoignent plusieurs tablettes d'argile de l'époque paléo-babylonienne[2]. Il n'y a aucune preuve archéologique qui permette de remonter plus avant, même si quelques hypothèses existent.
Ainsi les travaux d'Alexander Thom, qui imagine une organisation de sites mégalithiques datant du XXVe siècle av. J.-C. en Grande-Bretagne et en France utilisant triangles rectangles et triplets pythagoriciens, sont fortement contestés[3]. L'hypothèse parfois avancée que le théorème aurait été connu de l'Égypte ancienne dès le Moyen Empire paraît elle aussi difficile à établir[4].
Mésopotamie


Les historiens des mathématiques et assyriologues[8] ont découvert à la fin des années 1920 que s'était forgée en Mésopotamie (l'ancien Irak), à l'époque paléo-babylonienne une culture mathématique dont l'objet n'était pas purement utilitariste[9](numération mésopotamienne finale : sexagésimale positionnelle avec base décimale accessoire).
Plusieurs des tablettes d'argile qui ont été retrouvées et analysées montrent que la relation entre les longueurs des côtés du rectangle et celle de sa diagonale (soit entre les longueurs des côtés d’un triangle rectangle) était connue[10] et utilisée pour résoudre des problèmes calculatoires[11].
Des "tablettes cadastrales" (dont la plus ancienne date de -2340 à -2200 ) établies pour le commerce ou l'administration de parcelles exposent ainsi cette connaissance. La tablette Si427[12] datant de -1900 à -1600 a été récemment[Quand ?] redécouverte par Daniel Mansfield (École de mathématiques et de statistiques de Sydney, Australie) au Istanbul Arkeoloji Müzeleri. Découverte à Sippar (Irak), elle montre ainsi un terrain avec tour, aire de battage et marécage dont une des parcelles a été mise en vente par son propriétaire. Elle présente des découpes de trapèzes et de triangles rectangles ainsi que quelques triplets pythagoriciens[13].
La tablette Plimpton 322 datant de vers -1800 donne une liste ordonnée de nombres associés à des triplets pythagoriciens, soit des entiers (a, b, c) satisfaisant la relation a2 + b2 = c2. La tablette ne donne que deux nombres du triplet, mais les associe explicitement au plus petit côté et à la diagonale d'un rectangle[1],[14],[15]. La première colonne ne contient pas un de 3 éléments du triplet mais une combinaison des 3 dont l'interprétation varie selon les hypothèses et les reconstitutions des parties manquantes. Ce pourrait être une tablette d'exercice pour étudiant mais la régularité des éléments laissent penser à une table. Les inscriptions sont en caractère cunéiforme, en base 60 avec numérotation de position[16].
Il n'y a pas trace de l'énoncé d'un théorème, et les historiens préfèrent souvent utiliser un autre mot, certains parlent par exemple de « règle de Pythagore »[17]. Ni celle-ci, ni le principe qui la sous-tend ne sont explicitement énoncés non plus, mais les exemples montrent bien qu'une règle générale est connue[18].
La datation et l'origine exacte des tablettes d'argile n'est pas toujours évidente, beaucoup de celles-ci ont été achetées sur le marché des antiquités comme la tablette Plimpton 322, mais les historiens peuvent s'appuyer sur des éléments linguistiques, et les similarités avec celles dont l'origine est connue, ayant été obtenues par des fouilles archéologiques régulières. Les traces que l'on a des cultures antérieures rendent peu vraisemblable la découverte de la « règle de Pythagore », avant -2300, celle-ci pourrait apparaître entre -2025 et -1825[19].
Inde
En Inde, un énoncé du théorème, sous sa forme la plus générale, apparaît dans l'Apastamba (en), l'un des Śulba-Sūtras, ces traités du cordeau qui codifient les règles des constructions destinées aux rituels védiques. Ceux-ci ont été rédigés entre le VIIIe et le IVe siècle avant notre ère (par ailleurs certains triplets pythagoriciens sont mentionnés dans des textes bien antérieurs). Les Sulbasutras parlent du rectangle et de sa diagonale, plutôt que de triangle[20].
Chine
Le théorème apparaît également en Chine dans le Zhoubi suanjing (« Le Classique mathématique du Gnomon des Zhou »), un des plus anciens ouvrages mathématiques chinois[21]. Ce dernier, écrit probablement durant la dynastie Han (206 av. J.-C. à 220), regroupe des techniques de calcul datant de la dynastie Zhou (Xe siècle av. J.-C. à -256). Le théorème ou procédure s’énonce de la manière suivante :
« En réunissant l’aire (mi) de la base (gou) et l’aire de la hauteur (gu), on engendre l’aire de l’hypoténuse. »
Mais la question se pose de savoir si ce théorème — ou cette procédure — était muni ou non d’une démonstration. Sur ce point les avis sont partagés[22]. Le théorème, sous le nom de Gougu (à partir des mots « base » et « altitude »), est repris dans le Jiuzhang suanshu (Les neuf chapitres sur l'art mathématique, 100 av. J.-C. à 50), avec une démonstration, utilisant un découpage et une reconstitution, qui ne ressemble pas à celle d’Euclide et qui illustre l'originalité du système démonstratif chinois[23].
Égypte ancienne
Aucun texte connu de l'Égypte antique ne permet d'attribuer aux Égyptiens une connaissance en rapport avec le théorème de Pythagore, avant un document écrit sur papyrus en démotique, généralement daté vers 300 av. J.-C. qui mentionne trois triplets pythagoriciens[24]. Ceci peut tenir à la fragilité du support employé : peu de textes mathématiques de l'Égypte antique nous sont parvenus. Mais le plus notable d'entre eux, le papyrus Rhind, une copie effectuée vers 1650 d'un document datant de 1800 av. J.-C., apparaît comme une somme des connaissances mathématiques de l'époque. Or ni triplets pythagoriciens, ni rien en rapport avec le théorème, n'y apparaît, ce qui laisse penser qu'il est ignoré à ces dates[25].
Il n'est cependant pas impossible que le triangle rectangle 3-4-5, celui dont les côtés correspondent au triplet pythagoricien le plus simple, soit connu en Égypte dès une époque assez ancienne. Plutarque décrit (à la fin du Ier siècle de notre ère) une interprétation symbolique religieuse du triangle[26]. Mais à l'époque de Plutarque, le syncrétisme religieux a cours dans l'Égypte sous domination romaine, après avoir été gouvernée par les Ptolémées, et il est délicat de déterminer l'origine de cette interprétation, encore plus de la dater[27].
L'hypothèse de l'utilisation en architecture du triangle 3-4-5 obtenu en utilisant des cordes, éventuellement pourvues de nœuds espacés régulièrement, et tendues en particulier pour tracer des angles droits, est pour le moins discutée[28],[29]. Les faces de la pyramide de Khephren ont une pente de 4/3, mais il existe des explications simples pour leur construction, qui ne supposent pas la connaissance du triangle correspondant[30]. Pour les tracés horizontaux, au vu de ce que l'on sait des cordes disponibles à l'époque et de leur élasticité, la précision de la méthode ne paraît pas compatible avec celle des constructions de grande dimension de l'Égypte antique[31], mais pourrait fonctionner pour des salles ou des édifices de plus petite dimension[32]. Ainsi le tracé d'une voûte elliptique datant de la XXe dynastie découvert par Georges Daressy correspond à une ellipse dont le foyer, le centre et une intersection avec le petit axe, forment un triangle 3-4-5. Par ailleurs une ellipse peut, elle-même, se tracer facilement à l'aide d'une corde tendue[33].
Il reste que la connaissance de ce que le triangle 3-4-5 est droit, même si elle n'a rien d'invraisemblable, n'attesterait de toute façon nullement que les carrés des côtés aient été comparés, encore moins de la connaissance du théorème de Pythagore[34].
Les Grecs : de Pythagore à Euclide
Le théorème et sa conclusion, accompagnés de démonstrations, concluent le livre I des Éléments d'Euclide, rédigés probablement au début du IIIe siècle av. J.-C.[35]. Le théorème lui-même est donné à la proposition XLVII sous la forme suivante[36] :
« Aux triangles rectangles, le carré du côté qui soutient l’angle droit, est égal aux carrés des deux autres côtés. »
Sa réciproque est la proposition XLVIII[36] :
« Si le carré de l’un des côtés d’un triangle est égal aux carrés des deux autres côtés, l’angle soutenu par ces côtés est droit. »

Proclus dans ses commentaires (autour de l’an 400) relate, avec scepticisme, que certains attribuent à Pythagore la découverte du théorème, et attribue à Euclide la démonstration qu'il donne dans ses Éléments[37]. Les témoignages connus au sujet des contributions mathématiques de Pythagore sont tardifs : au plus tôt du Ier siècle av. J.-C., alors que Pythagore aurait vécu au VIe siècle avant notre ère. Un distique attribué à Apollodore de Cyzique (IVe siècle av. J.-C.) et cité par Plutarque (Ier siècle de notre ère) pourrait faire exception s'il s'agit bien du théorème[38], mais Plutarque lui-même en doute[39]. L'identité exacte de l'auteur du distique, et donc la date de sa composition, n'ont d'ailleurs elles-mêmes rien d'évident[38]. Il n'y a cependant aucun doute que le théorème était connu des Grecs bien avant Euclide, par exemple Hippocrate de Chio (Ve siècle av. J.-C.), l'auteur du théorème des deux lunules, ne pouvait l'ignorer. Aussi certains historiens ont tenté de reconstituer leurs démonstrations, celle d'Euclide ayant pu être contrainte par la structure de son traité axiomatique. Ainsi n'a-t-il pas encore abordé les proportions quand il démontre le théorème de l'hypoténuse au livre I, ce qui lui interdit une démonstration analogue à celle par les triangles semblables[40].
Incommensurabilité
Le théorème de Pythagore joue un rôle dans la découverte par les mathématiciens grecs, probablement au Ve siècle av. J.-C., de grandeurs incommensurables (qui ne peuvent pas être mesurées avec une même unité), prémisse des nombres irrationnels, en particulier à travers le cas particulier du triangle rectangle isocèle, pour lequel on dispose d'une démonstration particulièrement simple par duplication du carré[41] : un carré dont le côté sert d’unité a une diagonale dont le carré de la longueur vaut 2.
L'incommensurabilité a pu être mise en évidence géométriquement, sans qu'il soit question de racine carrée donc sans recourir au théorème de Pythagore[42], mais le théorème de Pythagore autorise une preuve arithmétique, dans le cas de la diagonale du carré en montrant qu'aucune fraction d’entiers n’a de carré égal à 2, soit l'irrationalité de [42].
Une thèse très répandue chez les historiens jusqu'au milieu du XXe siècle, mais discutée ensuite, est que l'incommensurabilité joue un rôle important dans le développement des mathématiques grecques pré-euclidiennes[43].
Démonstrations
Plusieurs centaines de démonstrations différentes[44] ont été répertoriées pour le théorème de Pythagore. La plupart sont construites sur des égalités d’aires obtenues par découpage et recollement, voire en utilisant des rapports d’aires de triangles semblables. La définition du produit scalaire en géométrie repérée fournit aussi une démonstration purement algébrique. De nombreuses autres démonstrations ont été recensées[44], utilisant des outils mathématiques variés. Léonard de Vinci[45] et le président américain James Garfield[46] en ont proposé.
Par soustraction d'aires
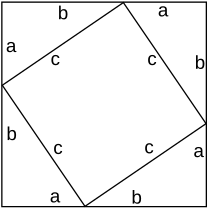

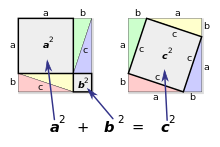
Pour un triangle rectangle donné, il est possible de l’inscrire en quatre exemplaires dans les coins d’un carré dont le côté a pour longueur la somme des longueurs des côtés de l'angle droit. Les quatre hypoténuses forment alors un carré, par égalité de longueur et sachant que chacun de ses angles est supplémentaire des deux angles aigus du triangle.
Avec les notations usuelles, l’aire totale du grand carré vaut donc (a + b)2 et l’aire du carré intérieur vaut c2. La différence est constituée par quatre triangles d’aire ab/2 chacun.
La relation algébrique entre ces aires s’écrit alors (a + b)2 = 4 (ab/2) + c2, c’est-à-dire a2 + 2ab + b2 = 2ab + c2, ce qui revient à a2 + b2 = c2.
Aucun calcul algébrique n'est cependant nécessaire : on peut conclure par un réarrangement des quatre triangles rectangles dans le grand carré, comme celui indiqué sur l'animation ou celui indiqué sur la figure à droite.
Par des triangles semblables

Il n’y a pas trace de la démonstration qu’aurait conçue Pythagore et les historiens envisagent deux types de démonstrations : ou bien une démonstration fondée sur un découpage comme celui de la section précédente ou le puzzle de Gougu, ou bien une démonstration utilisant les proportionnalités des triangles découpés par la hauteur issue de l’angle droit[47]. Une telle démonstration est donnée par Euclide à la proposition 31 du Livre VI des Éléments (pour une généralisation du théorème)[48].
En effet, soit H le pied de la hauteur issue de C dans le triangle ACB rectangle en C. Alors les deux triangles rectangles AHC et CHB sont semblables au triangle initial, par égalités des angles, puisqu'ils partagent à chaque fois un des angles non droits[49].
Ensuite deux variantes sont possibles.
Par les aires des triangles semblables
Cette démonstration[50] s'appuie sur L'égalité des aires :
- Aire(AHC) + Aire (CHB) = Aire(ACB)
Les aires des trois triangles semblables AHC, CHB et ACB, portées par les côtés AC, CB et AB sont proportionnelles aux carrés de ces côtés[Note 1]. L'égalité précédente donne donc le théorème de Pythagore, en simplifiant par le coefficient de proportionnalité :
- AC2 + BC2 = AB2.
Cette démonstration n'est cependant pas exactement celle du livre VI des Éléments, même si elle n'utilise que des résultats de l'exposé euclidien disponibles à la proposition 31[51].
Par AB = AH + HB
Dans sa démonstration de la proposition 31, Euclide utilise directement :
- AB = AH + HB
en montrant que AH est, relativement à AB, comme le carré de AC relativement à celui de AB, de même que HB est, relativement à AB, comme le carré de CB relativement à celui de AB d'où le résultat[52]. En détaillant, et modernisant[53], les triangles HAC et CAB sont semblables donc :
- AHAC = ACAB, soit AH×AB = AC2. (1)
De même, les triangles HCB et CAB étant semblables :
- HBCB = CBAB, soit HB×AB = BC2. (2)
Comme AB = AH + HB, en additionnant (1) et (2), on obtient : AB2 = AC2 + BC2.
Selon Euclide, livre I
![Figure dite du moulin à vent, avec un triangle ABC sur les côtés duquel sont formés trois carrés BCED, ABFG et ACIH. La hauteur de ABC issue de A coupe [BC] en J et [DE] en K.](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/PythagoreEuclide0.svg/310px-PythagoreEuclide0.svg.png)
La démonstration présentée par Euclide dans le livre I des Éléments[54] s’appuie sur les précédentes propositions, en particulier la proposition 4 — en termes modernes deux triangles ayant un angle de même mesure entre deux côtés de mêmes longueurs sont isométriques, et la proposition 41 du livre I sur aire d'un triangle :
« Si un parallélogramme et un triangle ont une même base, et sont entre mêmes parallèles ; le parallélogramme sera [d’aire] double du triangle. »
Sur les côtés d’un triangle ABC rectangle en A, sont construits extérieurement des carrés BCED, ABFG et ACIH. La hauteur de ABC issue de A coupe le côté opposé [BC] en J et le segment [DE] en K.
Il s’agit de démontrer que l’aire du carré BCED est égale à la somme des aires des carrés ABFG et ACIH.
Les triangles BCF et ABD ont même angle en B (c’est-à-dire l’angle du triangle ABC augmenté d’un angle droit) et par construction, BF = AB et BC = BD. Donc les triangles BCF et ABD ont même aire. Or d’après la proposition 41, l’aire du triangle BCF vaut la moitié de celle du carré ABFG et l’aire du triangle ABD vaut la moitié de celle du rectangle BDKJ. Donc le carré ABFG et le rectangle BDKJ ont même aire.
De même, les triangles BCI et ACE ont même angle en C avec les égalités AC = CI et BC = CE donc ils ont même aire, donc d’après la proposition 41, le carré ACIH a même aire que le rectangle CEKJ.
Finalement, le carré BCED se décompose en deux rectangles BDKJ et CEKJ, dont les aires sont celles de ABFG et ACIH respectivement, ce qui termine la démonstration.
Pappus d'Alexandrie donne une démonstration de son théorème sur les aires, pour un triangle quelconque sur les côtés duquel sont construits des parallélogrammes, qui fournit en la particularisant au triangle rectangle sur les côtés duquel sont construits des carrés, une démonstration du théorème de Pythagore alternative à celle d'Euclide, qui utilise des parallélogrammes plutôt que des triangles, et qui pourrait s'insérer au même endroit de l'exposé euclidien[55].
Par le puzzle de Gougu
Le théorème de Gougu[56],[57] de gou (base) et gu (hauteur)[58] est reconstitué d’après les commentaires du mathématicien chinois Liu Hui (IIIe siècle apr. J.-C.) sur le Jiuzhang suanzhu 九章算術 « Les Neuf Chapitres sur l'art mathématique » (206 av.–220 apr. J.-C.), et le Zhoubi Suanjing 周髀算經, « Le Classique mathématique du Gnomon des Zhou » (un livre d’astronomie). Le neuvième chapitre du livre Les neuf chapitres, classique mathématique de la Chine ancienne, s’ouvre sur un énoncé du théorème de Pythagore avec le commentaire laconique : « la base multipliée par elle-même fait un carré vermillon, la hauteur multipliée par elle-même un carré bleu-vert et l’on fait en sorte que ce qui entre et ce qui sort se compense l’un l’autre (...) alors (...) on engendre par réunion l’aire du carré de l’hypoténuse ». Cette preuve utilise le principe du puzzle : deux surfaces égales après découpage fini et recomposition ont même aire. Euclide, dans sa propriété de cisaillement, utilise le même principe.
L’absence d’illustration associée à ce commentaire réduit les historiens à émettre des conjectures pour sa reconstitution. Le dessin ci-contre est proposé par Jean-Claude Martzloff[59] d’après une édition de 1892 des Neuf chapitres. Le triangle rectangle y est tracé en gras, le carré de la hauteur a été tracé à l’extérieur du triangle, le carré de la base et celui de l’hypoténuse sont tournés vers le triangle. Les parties des carrés des côtés de l’angle droit qui dépassent du carré de l’hypoténuse ont été découpées et replacées à l’intérieur de ce carré. Le triangle rouge est égal au triangle de départ. Le triangle jaune a pour grand côté de l’angle droit le petit côté du triangle de départ et a mêmes angles que le triangle initial. Le triangle bleu a pour grand côté de l’angle droit, la différence des côtés du triangle initial et a mêmes angles que le triangle initial.
Karine Chemla[60] appuie plutôt son raisonnement sur une figure fondamentale associée au texte du Zhoubi suanjing et formée d’un triangle 3 - 4 - 5 dans laquelle on peut lire de nombreuses relations liant les trois côtés du triangle rectangle. Elle interprète le commentaire de Liu Hui comme une nouvelle lecture de la figure fondamentale avec déplacement des 3 pièces 1 - 2 - 3 de l’extérieur du carré dans le carré de l’hypoténuse.
 c2 = 4 (ab)/2 + (b – a)2 ou bien aussi (a + b)2 – 4ab/2 = c2. |
 |
 |
Quant à Li Jimin[61], il attribue au Zhoubi Suanjian la paternité de la première démonstration, il s’appuie lui aussi sur la figure fondamentale et fait pivoter les triangles (1-2) et 3 sur leur pointe pour les installer dans le carré de l’hypoténuse. Un tel découpage, avec pivotement des deux triangles, apparaît également en Europe au XIXe siècle chez George Biddell Airy et Philip Kelland[62].

Par le produit scalaire
Cette preuve s'inscrit dans un contexte tout à fait différent. Dans un espace vectoriel euclidien, les définitions mêmes de la norme, du produit scalaire et de l'orthogonalité sont déjà d'une certaine façon associées à une forme du théorème de Pythagore (voir ci-dessus).
Par bilinéarité du produit scalaire, pour deux vecteurs quelconques et :
- ,
soit :
- ,
ce qui, en définissant l'orthogonalité de deux vecteurs par la nullité de leur produit scalaire, fournit une version vectorielle du théorème de Pythagore (et de sa réciproque).
Dans un espace affine euclidien la longueur AB d'un segment [AB] est la norme du vecteur . Les vecteurs portés par les côtés d’un triangle ABC vérifient la relation de Chasles :
et le résultat précédent donne :
- .
autrement dit le théorème de Pythagore et sa réciproque, quand l'orthogonalité est définie par la nullité du produit scalaire.
Visualisation par des méthodes physiques

Le théorème de Pythagore étant un théorème portant sur des aires, celles des carrés dont les bases sont les côtés du triangle, on peut le visualiser grâce à des réservoirs de liquide de volume proportionnel aux différentes aires. On peut alors constater que le volume du plus grand réservoir est égal à la somme des volumes des deux autres réservoirs plus petits. Il ne s'agit cependant pas d'une démonstration. On peut également citer d'autres méthodes non mathématiques, par exemple il en existe une mécanique utilisant un équilibre de forces[63].
Généralisations
Pour un triangle quelconque

La loi des cosinus ou théorème d'Al-Kashi donne une formule faisant intervenir les longueurs des côtés et le cosinus de l'un des angles d'un triangle quelconque. L’angle de mesure γ, le côté opposé de longueur c et les deux autres côtés de longueurs respectives a et b sont reliés par la relation :
.
Si l’angle γ est droit, son cosinus est nul et la formule se réduit à la relation du théorème de Pythagore. S'il n'est pas droit, le cosinus de l'angle γ est non nul, ce qui donne la réciproque. Cette généralisation permet de traiter des problèmes de calcul d’angles et de distances dans un triangle quelconque.

Avec d'autres figures formées sur les côtés
Euclide mentionne dans les Éléments[36] (proposition 31 du livre VI) :
« Dans les triangles rectangles, la figure construite sur l’hypoténuse est équivalente à la somme des figures semblables et semblablement construites sur les côtés qui comprennent l’angle droit. »
En appliquant cette généralisation à des demi-disques formés sur chaque côté d’un triangle rectangle, il en découle le théorème des deux lunules, selon lequel l’aire du triangle rectangle est égale à la somme des aires des lunules dessinées sur chaque côté de l’angle droit.

À un triangle quelconque et à des parallélogrammes
Pappus d'Alexandrie, à la proposition 1 du livre IV de sa Collection Mathématique[64], donne une autre généralisation — nommée souvent en France théorème de Clairaut — valable sur un triangle quelconque, sur les côtés duquel sont construits des parallélogrammes : sur le dessin ci-contre, la somme des aires des deux parallélogrammes en gris foncé égale celle du parallélogramme en gris clair. Pappus prenait le parallélogramme BUVC, plutôt que LBCM dont il est le translaté.
En plus grande dimension
L’hypoténuse d’un triangle rectangle pouvant se concevoir comme la diagonale d’un rectangle, une généralisation du théorème en dimension supérieure peut s’énoncer comme suit :
Dans un pavé droit, le carré de la grande diagonale est égal à la somme des carrés des dimensions du pavé.
Ce résultat est équivalent au calcul de la longueur d’un segment à partir des coordonnées cartésiennes de ses extrémités dans un repère orthonormé :
ou, en dimension supérieure, si A est de coordonnées (xi) et B de coordonnées (x'i) :
.
Cette dernière formule est encore valable dans un espace de Hilbert de dimension infinie et aboutit notamment à la formule de Parseval.
Le théorème de Gua donne une autre généralisation du théorème de Pythagore dans un espace euclidien : si un tétraèdre a toutes ses arêtes orthogonales en un sommet alors le carré de l’aire de la face opposée au coin est la somme des carrés des aires des trois autres faces.
En arithmétique : le théorème de Fermat-Wiles

La recherche exhaustive des triplets pythagoriciens est un problème arithmétique à part entière. Elle a pu être motivée par la construction de triangles rectangles dont les longueurs des côtés sont commensurables. Elle ouvre la porte à la recherche de triplets satisfaisant une équation plus générale : an + bn = cn, où l’exposant n est un entier supérieur à 2. L’absence de solution lorsque l’exposant est supérieur ou égal à 3 est la conjecture de Fermat, qui n’a été définitivement démontrée que plus de trois siècles plus tard par Andrew Wiles.
En géométrie non euclidienne
Le théorème de Pythagore est équivalent (en admettant les autres axiomes de la géométrie) à l'axiome des parallèles[65], qui peut être rédigé ainsi :
Axiome des parallèles — Par un point, il passe une et une seule droite parallèle à une droite donnée.
Cela signifie que, dans les axiomes de la géométrie euclidienne, on peut remplacer l'« axiome » des parallèles par le « théorème » de Pythagore sans que les autres résultats de la géométrie soient modifiés. Les statuts d'axiome et de théorème de ces deux résultats sont alors inversés : le « théorème » de Pythagore devient un axiome (une vérité de base, indémontrable, sur laquelle s'appuie la théorie) et l'« axiome » des parallèles devient un théorème, qui peut être démontré à l'aide de Pythagore.
Dans d'autres géométries, l'axiome des parallèles est remplacé par un autre qui le contredit, et le théorème de Pythagore n'est donc plus vrai.

En trigonométrie sphérique, si un triangle est formé par trois arcs de grands cercles à la surface d’une sphère de rayon R et si deux de ces arcs se croisent à angle droit, la relation du théorème de Pythagore n’est plus valable, comme dans le cas du triangle équilatéral trirectangle. Elle doit être remplacée par la formule[66] :
où est la longueur de l’arc opposé à l’angle droit.
Une relation similaire existe en géométrie hyperbolique[67] pour une courbure constante égale à −1/R :
où cosh désigne la fonction cosinus hyperbolique.
Dans les deux cas, un développement limité à l’ordre 2 redonne, pour des triangles de faible dimension, la relation du théorème de Pythagore en géométrie plane.
Plus généralement, la propriété résiste mal au transfert dans d’autres géométries à cause de leur courbure :
- si la courbure est positive : ;
- si la courbure est négative : ;
- si la courbure est nulle : .
Dans le cadre de la relativité générale, l’espace euclidien est remplacé par un espace courbe où les segments sont remplacés par des géodésiques. La théorie de la relativité générale soutient que la matière et l’énergie conduisent l’espace à être non euclidien et le théorème ne s’applique donc pas strictement en présence d’énergie. Cependant, la déviation par rapport à l’espace euclidien est faible sauf auprès d’imposantes sources gravitationnelles comme les trous noirs. Déterminer si le théorème est enfreint sur d’importantes échelles cosmologiques, c’est-à-dire mesurer la courbure de l’Univers, est un problème ouvert pour la cosmologie.
Calcul numérique
En informatique, le calcul direct de la longueur de l'hypoténuse par le théorème de Pythagore, par élévation au carré puis racine carrée de la somme, peut conduire pour des valeurs extrêmes (très grandes ou très faibles en valeur absolue) à des erreurs de dépassement ou de soupassement : l'étape intermédiaire d'élévation au carré peut mener à des résultats non représentables, par exemple pour la norme très utilisée IEEE 754, et donc à un résultat final de 0 ou « infini », alors même que le résultat final est lui-même représentable. L'algorithme de Moler-Morrisson, dérivé de la méthode de Halley, est une méthode itérative efficace qui évite ce problème[68].
Culture
Le théorème de Pythagore est mentionné dans La Planète des singes, de Pierre Boulle. Le narrateur, considéré comme un animal dépourvu d’intelligence, détrompe en effet son interlocuteur en traçant une figure géométrique qui illustre le théorème.
Le chansonnier Franc-Nohain a composé un quatrain qui cite le théorème[69] :
Le carré de l’hypoténuse
Est égal, si je ne m’abuse
À la somme des carrés
Construits sur les autres côtés.
Notes et références
Notes
- C'est, pour des triangles semblables quelconques, la proposition 19 du livre VI (Vitrac 1994, p. 199). De façon plus moderne : les hauteurs des triangles semblables étant dans le même rapport que les côtés, le calcul de l'aire du triangle donne immédiatement le résultat.
- Le commentaire du Zhoubi suanjing consiste à remarquer que le carré de l’hypoténuse est formé de 4 triangles vermillon d’aire ab/2 et d’un carré jaune central d’aire (b – a)2.
Références
- Pour une description de la tablette et diverses interprétations, voir Robson 2002.
- Høyrup 1998.
- Voir Olivier Keller, « Préhistoire de la géométrie : le problème des sources », sur IREM de La Réunion, ; voir également Maurice Caveing, Le Problème des objets dans la pensée mathématique : problèmes et controverses, Vrin, (lire en ligne), p. 56, qui critique l'utilisation des travaux de Thom par Bartel Leendert van der Waerden dans (en) Geometry and Algebra in Ancient Civilizations, Springer Verlag, .
- Le Papyrus Berlin 6619 qui peut dater du XIXe siècle av. J.-C. est parfois évoqué, mais cela est très contesté (Rossi 2007, p. 217). Il présente bien un problème du second degré dont la solution met en jeu implicitement le triplet (3, 4, 5), mais il n'est pas question de triangle rectangle. Voir également ci-dessous le paragraphe Égypte ancienne.
- Voir Høyrup 1998, p. 396, la solution est décrite de façon procédurale, voir (en) Duncan J. Melville, « Poles and walls in Mesopotamia and Egypt », Historia Mathematica, vol. 31, , p. 148–162 (lire en ligne).
- Melville 2004.
- Éliane Cousquer, « Le Théorème de Pythagore » [PDF].
- Autour d'Otto Neugebauer en Allemagne, puis de François Thureau-Dangin en France, voir (en) Jens Høyrup, « Changing Trends in the Historiography of Mesopotamian Mathematics: An Insider's View », History of Science, vol. 34, , p. 1-32 (lire en ligne).
- Høyrup 1998, p. 393.
- E.M. Bruins, « Aperçu sur les mathématiques babyloniennes », Revue d'histoire des sciences et de leurs applications, vol. 3, no 4, , p. 312 (lire en ligne).
- Plusieurs sont décrits par Høyrup 1998.
- Guru Med, « Le plus ancien exemple de géométrie appliquée a été découvert dans une tablette d'argile babylonienne vieille de 3 700 ans », sur GuruMeditation, (consulté le )
- Olivier Donnars, « Le théorème d'avant Pythagore », Science et vie,
- https://doi.org/10.1016/j.hm.2017.08.001
- Plimpton 322: A Study of Rectangles
- Georges Ifrah, Histoire universelle des chiffres : l'intelligence des hommes racontée par les nombres et le calcul, R. Laffont, (ISBN 2-221-07838-1, 978-2-221-07838-9 et 2-221-05779-1, OCLC 32511226, lire en ligne), p359
- Robson 2002, Høyrup 1998.
- Høyrup 1998, p. 402.
- Høyrup 1998, p. 406-407.
- Vitrac 1990, p. 315.
- Martzloff 2006, p. 13.
- Chemla et Shuchun 2005, p. 681.
- Jean-Claude Martzloff, « Quelques exemples de démonstration en mathématiques chinoises », dans La démonstration mathématique dans l’histoire, IREM de Lyon, , p. 131-132.
- Rossi 2007, p. 64.
- Maor 2007, p. 14.
- Il s'agit du traité sur Isis et Osiris, dans les Œuvres morales, voir De Isis et Osiris, une traduction du texte de Plutarque.
- Rossi 2007, p. 64-65.
- Maor 2007, p. 14-15.
- L'usage de cordes pour l'arpentage est quant à lui bien attesté, il est représenté dans des tombes de la XVIIIe dynastie (Rossi 2007, p. 154.), mais sans trace de nœuds (Rossi 2007, p. 155-156).
- Rossi 2007, p. 221.
- Rossi 2007, p. 155.
- De nombreuses tentatives de reconstitutions de plans d'édifices à partir de triangles (pas forcément rectangles) ont eu lieu depuis le XIXe siècle (Rossi 2007, p. 7-28). Parmi les plus récentes : Jean-Philippe Lauer utilise le triangle 3-4-5, compte-rendu critique et références (Rossi 2007, p. 158-161.), Alexandre Badawy l'utilise accompagné d'autres triangles, compte-rendu critique et références (Rossi 2007, p. 32-56).
- Rossi 2007, p. 117. ; cet exemple est jugé le plus convaincant pour une relation entre l'utilisation de cordes et le triangle 3-4-5 par Rossi 2007, p. 159.
- Rossi 2007, p. 218.
- Caveing, « Introduction générale », p. 15, in Vitrac 1990.
- Éléments d'Euclide, traduction Henrion Référence, document en ligne sur le site de la BNF (Ressources Gallica). Livre I (cisaillement proposition XXXV p. 62, parallélogramme et triangle de même base proposition XLI p. 69, le théorème proposition XLVII p. 76, réciproque proposition XLVIII p. 78) et Livre VI (généralisation aux figures semblables proposition XXXI p. 241).
- Éliane Cousquer, « Le Théorème de Pythagore », p. 10-11.
- Vitrac 1990, p. 311.
- Vitrac 1990, p. 377.
- Vitrac 1990, p. 313.
- Vitrac 1990, p. 314.
- Maurice Caveing, La figure et le nombre : Recherches sur les premières mathématiques des Grecs, Presses universitaires du Septentrion, , 424 p. (ISBN 978-2-85939-494-3, lire en ligne), p. 183.
- (en) Ken Saito, « Studies on proportion theory and incommensurability (introduction) », dans Jean Christianidis (ed.), Classics in the History of Greek Mathematics, Springer, (ISBN 978-90-481-5850-8), p. 187-189.
- (en) Alexander Bogomolny, « Pythagorean theorem », Cut The Knot, propose 99 démonstrations différentes du théorème mais cite The Pythagorean Proposition (par Elisha Scott Loomis, au début du XXe siècle) qui en rassemble 367.
- (en) Alexander Bogomolny, « Pythagorean theorem », Cut The Knot, proof 16.
- (en) Alexander Bogomolny, « Pythagorean theorem », Cut The Knot, proof 5.
- Éliane Cousquer, « Le Théorème de Pythagore » p. 13.
- Vitrac 1994, p. 236-237.
- C'est la proposition VI. 8 d'Euclide (Vitrac 1994, p. 176).
- Une telle démonstration est donnée par exemple dans Rudolf Bkouche, « Sur les démonstrations du théorème de Pythagore », APMEP, no 523, , p. 12 (lire en ligne [PDF]).
- Bkouche 2017, p. 198.
- Vitrac 1994, p. 237 ; Euclide parle de [segments de] droites, et non de longueurs, et de figures semblables sur les côtés, et non de carré d'une longueur.
- Voir Cousquer, p. 13 pour une présentation similaire de cette démonstration.
- Vitrac 19990, p. 282-284.
- Celle-ci est détaillée dans Vitrac 1990, p. 285-287. Le principe est celui de la démonstration donnée dans l'article « Théorème de Clairaut (géométrie) ».
- (en) « Proof of Guogu or Pythagoras' Theorem », sur chinapage.com.
- Martzloff 1990.
- Chemla et Shuchun 2005, chap. 9.
- Martzloff 2006, p. 297.
- Chemla et Shuchun 2005, p. 680.
- Karine Chemla dans (Chemla et Shuchun 2005) fait référence à l’interprétation (1993) de cet historien p. 682.
- Serge Cantat, « Découpage d’Airy et théorème de Pythagore », sur Images des mathématiques, .
- On trouvera cette démonstration ici, et une critique détaillée de cette démonstration (en) sur le site Cut The Knot.
- Vitrac 1990, p. 285-286.
- (en) Scott E. Brodie, « The Pythagorean Theorem is Equivalent to the Parallel Postulate », Cut The Knot.
- Franz Brünnow, Traité d'astronomie sphérique et d'astronomie pratique : Astronomie sphérique, Gauthier-Villars, 1869, Formules relatives aux triangles rectangles, p. 13.
- Saul Stahl, The Poincaré half-plane : a gateway to modern geometry, Jones & Bartlett Learning, , 298 p. (ISBN 0-86720-298-X, lire en ligne), chap. 8. 2 (« Hyperbolic right triangle »), p. 122.
- (en) Augustin A. Dubrulle, « A Class of Numerical Methods for the Computation of Pythagorean Sums », IBM Journal of Research and Development, vol. 27, no 6, , p. 582–589 (DOI 10.1147/rd.276.0582, CiteSeerx 10.1.1.94.3443, lire en ligne).
- Entrée « Pythagore (théorème de) » dans Baruk 1992.
Voir aussi
Bibliographie
- Stella Baruk, Dictionnaire de mathématiques élémentaires, [détail de l’édition]
- Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition]
- (en) Christopher Cullen (de), Astronomy and Mathematics in Ancient China : The ‘Zhou Bi Suan Jing’, CUP, , 241 p. (ISBN 978-0-521-03537-8, lire en ligne)
- (en) Jens Høyrup, « Pythagorean ‘Rule’ and ‘Theorem’ – Mirror of the Relation Between Babylonian and Greek Mathematics », dans Johannes Renger (ed.), Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft, 24.–26. März 1998 in Berlin, Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag, (lire en ligne), p. 393–407
- (en) Eli Maor, The Pythagorean Theorem : A 4,000-Year History, Princeton, New Jersey, Princeton University Press, , 259 p. (ISBN 978-0-691-12526-8, lire en ligne)
- (en) Jean-Claude Martzloff, A History of Chinese Mathematics, Springer, (ISBN 3-540-33782-2)
- (en) Eleanor Robson, « Words and pictures: new light on Plimpton 322 », Amer. Math. Month., vol. 109, no 2, , p. 105–120 (DOI 10.2307/2695324, lire en ligne).
- (en) Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, , 280 p. (ISBN 978-0-521-69053-9)
- Bernard Vitrac, Euclide Les Éléments Volume 1. Introduction générale (Maurice Caveing). Livres I à IV, PUF, (ISBN 2130432409), en particulier notices du Livre I, Sur Pythagore et le « théorème de Pythagore », p. 311-321.
- Bernard Vitrac, Euclide Les Éléments Volume 2. Livres V à IX, PUF, (ISBN 2130455689), en particulier le livre VI, avec une généralisation et une démonstration (indépendante de celle du livre I) proposition 31, p. 236.
Articles connexes
- Contexte
- Problèmes reliés
- Généralisations
- Théorème de Clairaut (géométrie), un cas plus général, avec des parallélogrammes autour d’un triangle quelconque
- Loi des cosinus (Le théorème de Pythagore généralisé) avec un peu de trigonométrie
- Ouverture
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :






















