Processus stationnaire
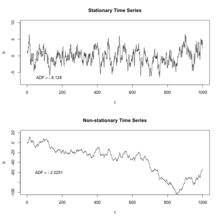
Pour accéder aux propriétés essentielles d'un signal physique il peut être commode de le considérer comme une réalisation d'un processus aléatoire (voir quelques précisions dans Processus continu). Le problème est largement simplifié si le processus associé au signal peut être considéré comme un processus stationnaire, c'est-à-dire si ses propriétés statistiques caractérisées par des espérances mathématiques sont indépendantes du temps. Lorsque cette hypothèse est vraisemblable, le processus bâti autour du signal est rendu ergodique, les moyennes temporelles étant identiques aux moyennes d'ensemble. On trouvera ci-dessous quelques éléments qui précisent un peu ces notions.
L'hypothèse stationnaire est admise dans de nombreux modèles théoriques, facile à réaliser dans des simulations numériques, beaucoup plus difficile voire impossible à justifier à propos d'un signal réel, faute de pouvoir accéder à d'autres réalisations du même processus. Il faut très généralement se contenter d'une justification grossière, utilisée par exemple dans l'analyse des enregistrements de vagues, qui consiste à dire qu'un enregistrement d'une vingtaine de minutes est assez court pour assurer la stationnarité (il est peu probable que les conditions météorologiques aient été modifiées) mais assez long pour qu'il fournisse des informations statistiques pertinentes.
Pour un autre point de vue voir Stationnarité d'une série temporelle.
Définitions[modifier | modifier le code]
Un processus est un ensemble de fonctions ordinaires , chacune d'elles étant une réalisation du processus. On peut caractériser ce processus en lui associant à chaque instant une densité de probabilité .
À une réalisation donnée on peut associer les moyennes temporelles
À la densité de probabilité on peut associer les moments appelés moyennes d'ensemble
Si ces moyennes d'ensemble, et par conséquent la densité de probabilité, ne dépendent pas de l'instant , on parle de processus stationnaire. Si, de plus, les moyennes temporelles leur sont égales, il s'agit d'un processus ergodique.
En fait, il ne s'agit là que des propriétés au premier ordre, les propriétés aux ordres supérieurs faisant intervenir la densité de probabilité jointe (voir Loi de probabilité à plusieurs variables) à des instants différents. Elles impliquent également des moyennes temporelles et des moyennes d'ensemble. Parmi ces dernières, la plus importante est l'autocovariance statistique . Si le processus est stationnaire et ergodique au second ordre, elle est identique à l'autocovariance temporelle, elle-même équivalente à la densité spectrale (voir Analyse spectrale).
La stationnarité au second ordre est suffisante pour assurer la stationnarité forte lorsque le processus peut être supposé gaussien, hypothèse souvent utilisée, parfois faute de mieux.
Quelques résultats[modifier | modifier le code]
Processus sinusoïdal[modifier | modifier le code]
Un tel processus est un ensemble de sinusoïdes de même fréquence et amplitude défini par
: constantes
: variable aléatoire distribuée uniformément sur un intervalle de largeur
La décomposition des puissances du cosinus montre qu'au premier ordre les moyennes d'ensemble sont indépendantes du temps (stationnarité) et identiques aux moyennes temporelles (ergodicité). Ce résultat se généralise à tous les ordres.
Les paragraphes qui suivent montrent comment il est possible de construire une multitude de processus possédant ces deux propriétés en partant de tels processus sinusoïdaux.
Sommes de processus[modifier | modifier le code]
Étant donnés deux processus aléatoires, les sommes de réalisations définissent les réalisations du processus somme. Celui-ci est stationnaire et ergodique si les deux processus sont eux-mêmes stationnaires, ergodiques et indépendants (voir la définition de l'indépendance dans Loi de probabilité à plusieurs variables).
Ce résultat se généralise à la somme d'un nombre quelconque de processus. Sous certaines conditions de régularité, on peut faire tendre ce nombre vers l'infini. Dans ce cas, il y a à chaque instant une somme de variables aléatoires indépendantes qui, selon le théorème central limite, tend vers une variable de Gauss. On parle alors de processus de Gauss. Ce résultat s'applique en particulier aux signaux physiques qui s'interprètent souvent comme des sommes de signaux élémentaires sinusoïdaux (voir Analyse spectrale).
Systèmes linéaires[modifier | modifier le code]
Une somme de processus sinusoïdaux se transforme en une somme de processus sinusoïdaux. La stationnarité et l'ergodicité sont donc conservées. Lorsque les processus composants sont indépendants, le caractère gaussien est également conservé.
Fonctions de processus[modifier | modifier le code]
Les moyennes du processus sont des moyennes du processus initial. La stationnarité et l'ergodicité se conservent donc. Elles se conservent également lorsque le monôme est remplacé par un polynôme. En passant à la limite, elles se conservent aussi pour une fonction régulière du processus initial .
Si le processus d'entrée est gaussien, le processus de sortie ne l'est plus mais l'interprétation du premier comme une somme de processus sinusoïdaux convient également pour le second. Un produit de cosinus de fréquences différentes étant égal à une somme de deux cosinus de fréquences somme et différence, à la différence de ce qui se produit avec un filtre linéaire le résultat contient des fréquences plus hautes et plus basses. On obtient ainsi un processus dans lequel, contrairement à ce qui a été exigé dans Sommes de processus, les composantes ne sont pas indépendantes mais le résultat reste néanmoins stationnaire et ergodique.
Livres[modifier | modifier le code]
- (en) Y. K. Lin, Probabilistic Theory of Structural Dynamics, New York, Robert E. Krieger Publishing Company, , 368 p. (ISBN 0882753770)







![{\displaystyle E[X(t_{0})^{n}]=\int _{-\infty }^{\infty }x^{n}p_{X}(x,t_{0}){\rm {d}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8012d4a01078a3f4c490182bdc13cbc307fb77e4)
![{\displaystyle E[X(t_{0})X(t_{0}+\tau )]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5b9b746d0802facd0b431930a36439f991f1e9b)





