Séquence principale

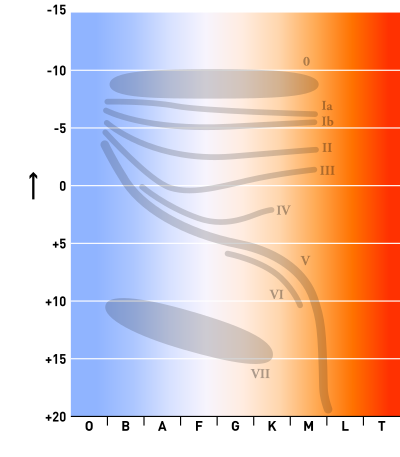
En astronomie, la séquence principale est une bande continue et bien distincte d'étoiles qui apparaissent sur des diagrammes où l'abscisse est l'indice de couleur B-V [note 1] et l'ordonnée la luminosité ou, en sens inverse, la magnitude absolue des étoiles. Ces diagrammes couleur-luminosité sont connus sous le nom de « diagrammes de Hertzsprung-Russell », d'après leur co-inventeurs Ejnar Hertzsprung et Henry Norris Russell. Les étoiles figurant dans cette bande sont connues sous le nom d’étoiles de la série principale, ou « étoiles naines »[1],[2]. Ainsi, environ 90 % des étoiles observées au-dessus de 0,5 M☉ sont sur la séquence principale[réf. nécessaire].
La séquence principale est aussi le stade principal de l'évolution d'une étoile. C'est pendant cette période que ses caractéristiques correspondent à celles de la séquence principale du diagramme Hertzsprung-Russell et qu'elle s'y trouve effectivement représentée.
La proportion élevée d'étoiles sur la séquence principale est due au fait que cette séquence correspond à la phase de fusion de l'hydrogène en hélium, laquelle dure la majeure partie de la durée de vie totale de l'étoile (en raison de la prépondérance de l'hydrogène dans la composition initiale et parce que la fusion d'hydrogène en hélium est la plus exoénergétique des réactions de fusion nucléaire).
Histoire[modifier | modifier le code]
Au début du XXe siècle, on commence à avoir des informations plus fiables sur les types et les distances des étoiles : elles montraient des spectres (à l'époque, leur partie visible) de structures différentes. Annie Jump Cannon et Edward Charles Pickering, au Harvard College Observatory (Observatoire de l'université Harvard) en déduisent alors une méthode de classification, connue sous le nom de Schéma de classification de Harvard, publiée dans les Annales de Harvard en 1901[3].
À Potsdam, en 1906, l'astronome danois Ejnar Hertzsprung remarque que les étoiles les plus rouges, classées K et M dans le schéma de Harvard, peuvent être sub-divisées en deux groupes bien séparés :
- celles qui sont beaucoup plus brillantes que le Soleil, qu'il nomme « géantes » ;
- et celles qui le sont beaucoup moins, les « naines ».
L'année suivante, il commence à étudier des amas stellaires ; c'est-à-dire de grands échantillons d'étoiles qui sont toutes à peu près à la même distance (le propre d'un amas est de regrouper de très nombreuses étoiles dans un espace de faible dimension). Il publie les premiers diagrammes de luminosité en fonction de la couleur pour ces étoiles. Ces diagrammes présentent une suite claire et continue d'étoiles, qu'il nomme « séquence principale »[4].
À l'université de Princeton, Henry Norris Russell poursuit ses recherches dans la même direction. Il étudie la relation entre classification spectrale et luminosité absolue, la magnitude absolue. À cette fin, il utilise un échantillon d'étoiles de parallaxes fiables, dont beaucoup ont été classifiées à Harvard. Quand il classe les types spectraux de ces étoiles en fonction de leur magnitude absolue, il trouve que les étoiles naines suivent une relation bien définie. Ceci lui permet de prédire la magnitude absolue d'une étoile avec une relative précision[5].
Parmi les étoiles rouges observées par Hertzsprung, les naines suivent aussi la relation couleur-luminosité découverte par Russell. Mais comme les géantes sont bien plus brillantes que les naines, elles ne suivent pas la même relation[6]. Russell propose que « les étoiles géantes doivent avoir une faible densité, ou une grande luminosité de surface, et inversement pour les étoiles naines ». Le même diagramme montre aussi qu'il y a quelques rares étoiles blanches très peu lumineuses[5].
En 1933, Bengt Strömgren introduit l'expression « diagramme de Hertzsprung-Russell » pour désigner un diagramme montrant la luminosité en fonction de la classe spectrale[7]. Ce nom renvoie à la mise au point de cette technique, en parallèle par Hertzsprung et Russell, au début du siècle[4].
Séquence principale[modifier | modifier le code]
Le théorème de Vogt-Russell, mis au point dans les années 1930, établit une relation entre la masse de l'étoile d'une part, le rayon et la luminosité de cette étoile de l'autre. Le diagramme HR utilisant ces mêmes valeurs, on peut déduire la masse et le rayon d'une étoile à partir de sa position dans le diagramme (cependant, on a découvert plus tard que le théorème n'est plus exact si la composition de l'étoile n'est pas uniforme)[8].
Un schéma amélioré pour la classification stellaire, dit « MK », a été publié en 1943 par W. W. Morgan et P. C. Keenan[9]. La classification MK donne à chaque étoile un type spectral basé sur la classification de Harvard – et une classe de luminosité. La classification de Harvard avait été mise au point en attribuant des lettres aux types d'étoiles en fonction de l'importance des diverses raies du spectre de l'hydrogène, avant que la relation entre spectre et température ne fût connue. Si on les range par ordre de température, et en éliminant les doublons, on obtient les types spectraux en fonction des températures décroissantes, avec des couleurs allant du bleu au rouge : la séquence devient O, B, A, F, G, K et M[note 2]. Les classes de luminosité vont de I à V, par ordre de luminosité décroissante. Les étoiles de luminosité V forment la séquence principale[10].
Étoiles de la séquence principale[modifier | modifier le code]
Quand une proto-étoile se forme dans l'effondrement d'un nuage moléculaire géant de gaz et de poussière dans le milieu interstellaire local (stellogénèse), elle est initialement homogène et se compose d'environ 70 % d'hydrogène et 28 % d'hélium, plus des traces des autres éléments[11]. La masse initiale de l'étoile dépend des conditions locales dans le nuage.
Pendant cet effondrement initial, l'étoile naissante dite précurseur de la séquence principale[réf. souhaitée] dégage de l'énergie (sous forme cinétique et de température notamment) par la pression interne qui en résulte. Quand la proto-étoile atteint une densité suffisante pour dépasser la barrière coulombienne, le processus de fusion nucléaire commence à transformer l'hydrogène en hélium dans le cœur, et à dégager ainsi davantage d'énergie[10] centrifuge, laquelle va peu à peu équilibrer l'énergie gravitationnelle essentiellement centripète.
La densité de l'étoile se stabilise et la fusion nucléaire de l'hydrogène devient le processus dominant de production d'énergie[12].
Équilibre[modifier | modifier le code]
Une fois qu'une étoile s'est formée, elle crée de l'énergie dans son cœur chaud et dense, par fusion nucléaire des noyaux d'hydrogène en noyaux d'hélium. Pendant cette période de la vie de l'étoile, elle se trouve sur la séquence principale du diagramme HR, à un point défini principalement par sa masse, avec quelques corrections dues essentiellement à sa composition chimique. La distribution des masses des étoiles nouvellement formées est décrite empiriquement par la fonction de masse initiale[13].
Toutes les étoiles de la séquence principale ont une région de cœur où l'énergie est produite par fusion nucléaire. La température et la densité de ce cœur sont à des niveaux suffisants pour entretenir la production d'énergie capable de soutenir le poids du reste de l'étoile. Une réduction de la production d'énergie produirait une compression par ce poids, ce qui rétablirait la production d'énergie à son niveau convenable, en raison de l'élévation de la pression et de la température. Inversement, un accroissement trop prononcé de la production d'énergie ferait gonfler l'étoile, diminuant ainsi la pression et la température du cœur. L'étoile forme donc un système auto-régulé en équilibre hydrostatique, stable tout au long de son séjour sur la séquence principale[14]. Toutes les étoiles de la séquence principale sont dans cet état stable, avec la pression thermique du cœur chaud qui équilibre la pression gravitationnelle des couches supérieures, et l'essentiel de leurs caractéristiques résultent de cet équilibre.
Répartition initiale[modifier | modifier le code]
Les caractéristiques de l'étoile déterminent sa place dans le diagramme de Hertzsprung-Russell, sur une courbe qui s'appelle la séquence principale standard[réf. nécessaire]. Les astronomes se réfèrent parfois à ce stade comme la séquence principale d'âge zéro (ZAMS, acronyme anglais pour Zero Age Main Sequence)[15]. La courbe ZAMS peut être calculée en utilisant des modèles numériques des propriétés stellaires au moment où l'étoile commence la fusion. À partir de ce point, la luminosité et la température de surface des étoiles augmentent en général avec l'âge[16],[17].
La majorité des étoiles sur un diagramme HR typique se trouvent sur la séquence principale. Cette ligne est accentuée parce que le type spectral et la luminosité ne dépendent que de la masse de l'étoile, au moins en première approximation, tant que l'étoile accomplit la fusion de l'hydrogène dans son cœur – et c'est ce que font presque toutes les étoiles pendant la majorité de leur vie active [18].
La variation d'intensité lumineuse entre les étoiles les moins chaudes est assez importante pour différencier les naines (rouges, orange ou jaunes) des plus grosses. Cependant, pour les étoiles plus chaudes (blanches et bleues), la variation de taille et de luminosité n'est pas directement observable[pourquoi ?] entre les étoiles. Pour cette raison, la nomenclature différencie les étoiles naines des géantes en se référant à la différence entre les spectres, dont les raies indiquent si l'étoile est sur la séquence principale ou en dehors. Néanmoins, des étoiles sur la séquence principale, même très chaudes et massives peuvent être appelées parfois naines[19].
D'autres facteurs contribuent à étaler la séquence principale sur le diagramme HR : incertitude sur la distance des étoiles, et présence d'étoiles binaires non résolues qui peuvent modifier les paramètres stellaires observés. Mais même une observation parfaite montrerait une séquence principale élargie, car la masse n'est pas le seul paramètre qui affecte la couleur et/ou la luminosité d'une étoile. Outre les variations en composition chimique – tant par l'abondance initiale que par l'évolution de l'étoile[20] – l'interaction avec un compagnon rapproché[21], une rotation rapide[22], ou un champ magnétique peut aussi changer la position d'une étoile légèrement sur le diagramme HR, pour citer quelques facteurs. Par exemple, il y a des étoiles très pauvres en éléments de numéro atomique supérieur à celui de l'hélium – ce sont les étoiles à faible métallicité – qui se trouvent juste en dessous de la séquence principale. Nommées sous-naines, ces étoiles effectuent la fusion de l'hydrogène dans leur cœur, et marquent la limite basse de la séquence principale, en ce qui concerne la composition chimique[23].
Une région presque verticale du diagramme HR, connue sous le nom de bande d'instabilité, est occupée par des étoiles variables pulsantes, notamment les céphéides. Ces étoiles varient en magnitude à intervalles réguliers, leur donnant une apparence pulsante. La bande coupe la partie supérieure de la séquence principale dans la région des classes A et F, entre 1 et 2 M☉. Les étoiles variables dans la partie de la zone d'instabilité qui coupe la partie supérieure de la séquence principale sont appelées variables de type Delta Scuti. Les étoiles de la séquence principale de cette région ne subissent que des changements de faible amplitude en magnitude, et cette variation est donc difficile à détecter[24]. D'autres classes d'étoiles de la séquence principale instables, comme les variables de type beta Cephei – distinctes des céphéides – ne sont pas reliées à cette bande d'instabilité.
Réactions nucléaires[modifier | modifier le code]

La chaîne PP et le cycle CNO interviennent quand les étoiles se trouvent sur la séquence principale tandis que la réaction triple α s'établit après qu'elles en soient sorties et si leurs caractéristiques leur permettent de devenir des étoiles géantes. À la température actuelle du cœur du Soleil, la chaîne pp domine encore.
Les étoiles de la séquence principale produisent leur énergie par deux processus de fusion de l'hydrogène, et le taux de production d'énergie par chacun dépend de la température au cœur. Les astronomes divisent alors la séquence principale en parties supérieure et inférieure, en fonction du mécanisme exact de la réaction de fusion nucléaire qui domine :
Les étoiles au-dessous d'une fois et demie la masse du Soleil (1,5 M☉) fusionnent surtout les noyaux d'hydrogène par fusion directe et désintégration β des isotopes de l'hydrogène : deutérium et tritium (chaîne pp). L'inférieure est celle où domine la chaîne pp[25] où les isotopes de l'hydrogène proton, deutérium et tritium fusionnent directement, le tritium subissant la désintégration β qui transforme lentement les protons en neutrons pour former les particules α.
C'est à une température de 18 millions de kelvins que le cycle CNO dépasse en productivité la chaîne pp. Ceci correspond à une étoile d'environ 1,5 M☉. Ainsi, les étoiles F ou moins chaudes utilisent la chaîne pp, tandis que les A ou plus chaudes utilisent le cycle CNO[16]. La transition d'un mode de production à l'autre s'effectue sur un intervalle de moins de 1 M☉ : dans le Soleil, seulement 1,5 % de l'énergie est produite par le cycle CNO[26]. Inversement, les étoiles de plus de 1,8 M☉ tirent presque toute leur énergie du cycle CNO[27]. Au-dessus de cette masse, la température centrale devient suffisante pour permettre la fusion de protons avec des noyaux de carbone (C), azote (N) et oxygène (O), et une chaîne utilisant ces noyaux comme intermédiaires, restitués après la production d'un noyau d'hélium se met en route. C'est le cycle CNO, qui dépasse rapidement en importance la chaîne proton-proton. La supérieure est celle où domine le cycle CNO, où les protons fusionnent avec des noyaux plus lourds, carbone, azote et oxygène, qui subissent la désintégration β et finalement éjectent un α pour recommencer le cycle.
La limite supérieure observée pour les étoiles de la séquence principale est de 120 à 200 M☉[28]. L'explication théorique pour cette limite est que les étoiles qui la dépassent ne peuvent pas rayonner l'énergie assez vite pour rester stables, si bien que toute masse additionnelle sera éjectée par une série de pulsations, jusqu'à ce que l'étoile atteigne une limite stable[29]. La limite inférieure pour une fusion nucléaire entretenue par la chaîne pp est d'environ 0,08 M☉[25]. En dessous de cette masse, on trouve des objets sous-stellaires qui n'entretiennent pas la fusion de l'hydrogène, et que l'on appelle naines brunes[30].
Rôle de la structure interne[modifier | modifier le code]

Comme il y a une différence de température entre le cœur et la surface, ou photosphère, l'énergie se propage vers l'extérieur. Les deux modes de transport de l'énergie sont la conduction et la convection. Dans la conduction, l'énergie est principalement transmise par rayonnement à ces températures. Une zone conductive est une zone stable par rapport à la convection, et il y a très peu de mélange de matière. Par contre, dans une zone convective, l'énergie est transportée par le plasma en mouvement : la matière est alternativement chauffée par le cœur et transportée vers l’extérieur, puis refroidie en surface par rayonnement et transportée vers l'intérieur. La convection est un mode plus efficace que la conduction pour le transport de l'énergie, mais elle n'aura lieu que dans des conditions qui créent un fort gradient de température, c'est-à-dire où la température varie rapidement avec la distance au centre[14],[31], par exemple une valeur élevée de l'opacité thermique qui limiterait la conduction. La zone de convection est donc située dans les couches extérieures de l'étoile, dans une zone fortement chauffée a sa base par le cœur et refroidie a sa périphérie par la couche extérieure de l'étoile[32].
Dans les étoiles massives (au-dessus de 10 M☉)[33], le taux de production d'énergie par le cycle CNO est très sensible à la température, si bien que la fusion est fortement concentrée dans le cœur. Donc il existe un fort gradient de température dans cette région, ce qui résulte en une zone convective assurant un meilleur transport de l'énergie[25]. Ce mélange de matière autour du cœur élimine l'hélium produit de la région fusionnant de l'hydrogène. Ceci permet à une fraction plus importante de l'hydrogène d'être consommée pendant le séjour sur la séquence principale. Par contre, les régions périphériques d'une étoile massive transportent l'énergie par conduction, avec pas ou peu de convection[14].
Pour les étoiles de masse plus faible, ce cœur convectif devient progressivement plus petit, et disparaît pour environ 2 M☉. C'est le cas pour des étoiles de masse intermédiaire, comme Sirius, qui transportent l'énergie majoritairement par conduction, avec une petite zone convective près du cœur[34]. En dessous, les étoiles comme le Soleil sont conductives près du cœur, mais convectives près de la surface : le cœur stable envers la convection s'enrichit en hélium et s'entoure de couches riches en hydrogène mélangées par la convection.
Et pour les étoiles de masse encore plus réduite, on arrive à des étoiles dont la zone de convection occupe l'ensemble de la masse : les étoiles de très petite masse, peu chaudes (en dessous de 0,4 M☉) sont convectives dans leur ensemble[13]. Ainsi l'hélium produit au cœur est réparti dans l'ensemble de l'étoile, produisant une atmosphère relativement uniforme, et une vie proportionnellement plus longue sur la séquence principale[14].
Luminosité[modifier | modifier le code]
La relation masse-luminosité exacte dépend de l'efficacité du transport de l'énergie du cœur vers la surface. Une opacité plus élevée a un effet isolant, qui retient plus d'énergie près du cœur, si bien que l'étoile n'a pas besoin de produire autant d'énergie pour maintenir l'équilibre hydrostatique. Inversement, une opacité plus faible entraîne que l'énergie s'échappe plus facilement, et l'étoile doit consommer plus de matière fusible pour maintenir l'équilibre[35]. Remarquer, cependant, qu'une opacité suffisamment élevée peut déclencher le transport de l'énergie par convection, ce qui change les conditions nécessaires pour maintenir l'équilibre[16].
Dans les étoiles de haute masse sur la séquence principale, l'opacité est dominée par la diffusion par les électrons, qui ne dépend pratiquement pas de la température. Donc la luminosité n'augmente plus que comme le cube de la masse de l'étoile[36]. Pour les étoiles en dessous de 10 M☉, l'opacité devient dépendante de la température, ce qui conduit à une variation de la luminosité approchant la 4e puissance de la masse de l'étoile[37]. Pour les étoiles de très petite masse, les molécules dans l'atmosphère contribuent aussi à l'opacité. En dessous d'environ 0,5 M☉, la luminosité de l'étoile varie comme la masse à la puissance 2,3, ce qui produit une diminution de la pente du graphique de la luminosité en fonction de la masse. Même ces raffinements ne sont cependant qu'une approximation, et la relation masse-luminosité peut dépendre de la composition de l'étoile[13].
Paramètres stellaires[modifier | modifier le code]
Table de paramètres stellaires de la séquence principale[38] K Exemples[39] Rayon Masse Luminosité Température O5 18 40 500 000 38 000 Zeta Puppis B0 7,4 18 20 000 30 000 Phi1 Orionis B5 3,8 6,5 800 16 400 Pi Andromedae A A0 2,5 3,2 80 10 800 Alpha Coronae Borealis A A5 1,7 2,1 20 8 620 Beta Pictoris F0 1,4 1,7 6 7 240 Gamma Virginis F5 1,2 1,29 2,5 6 540 Eta Arietis (en) G0 1,05 1,10 1,26 6 000 Beta Comae Berenices G2 1,00[note 3] 1,00[note 3] 1,00[note 3] 5 750 Soleil G5 0,93 0,93 0,79 5 560 Alpha Mensae K0 0,85 0,78 0,40 5 150 70 Ophiuchi A K5 0,74 0,69 0,16 4 640[40] 61 Cygni A M0 0,63 0,47 0,063 3 920 Gliese 185[41] M5 0,32 0,21 0,0079 3 120 EZ Aquarii A M8 0,13 0,10 0,0008 ~ 2 600 Étoile de Van Biesbroeck[42]
La température d'une étoile détermine son type spectral par son effet sur les propriétés physiques du plasma de sa photosphère. L'émission d'énergie d'une étoile en fonction de la longueur d'onde est influencée à la fois par la température et par la composition chimique. Un indicateur clé dans cette distribution d'énergie est donné par l'indice de couleur B − V, qui mesure la différence de magnitude apparente de l'étoile vue à travers un filtre standard bleu (B) et un filtre standard vert-jaune (V)[note 4]. Cette différence de magnitude constitue une mesure de la température de l'étoile.
Si l'on traite l'étoile comme un radiateur d'énergie idéal, connu sous le nom de corps noir, on peut relier la luminosité L et le rayon R à la température effective d'après la loi de Stefan-Boltzmann par :
où σ est la constante de Stefan-Boltzmann. Comme la position d'une étoile sur le diagramme HR donne une évaluation de sa luminosité, cette relation peut être utilisée pour estimer son rayon[43].
Les valeurs de la luminosité (L), du rayon (R) et de la masse (M) sont relatives à celles du Soleil, une étoile naine de classification spectrale G2 V. Les valeurs réelles pour une étoile peuvent différer de 20 à 30 % des valeurs listées ci-contre[44].
Trajectoires d'évolution[modifier | modifier le code]
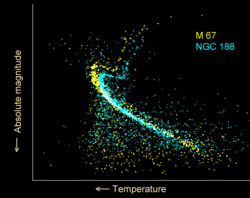
Une étoile va rester près de la position initiale sur la séquence principale jusqu'à ce qu'une partie importante de l'hydrogène de son cœur soit consommée. Elle commence alors à évoluer vers une étoile plus lumineuse. (Sur le diagramme HR, l'étoile se déplace vers le haut et vers la droite de la séquence principale.)
Au fur et à mesure que l'hélium inutilisable s'accumule dans le cœur d'une étoile de la séquence principale, la diminution de l'hydrogène par unité de masse amène une baisse graduelle du taux de fusion dans la masse. Pour compenser cet effet, la température et la pression du cœur augmentent graduellement, ce qui provoque une production totale d'énergie augmentée (pour soutenir la densité accrue de l'intérieur). Ceci produit une croissance lente, mais continue de la luminosité et du rayon de l'étoile dans le temps[16]. Ainsi, par exemple, la luminosité du Soleil à ses débuts n'était que 70 % de sa valeur actuelle[45]. Avec l'âge, la position d'une étoile va changer sa position vers le haut sur le diagramme HR. Ceci résulte en un élargissement de la bande de la séquence principale, parce que les étoiles sont observées à des fractions aléatoires de leur temps de vie. La séquence principale observée dans son ensemble est une bande plus large que la seule ZAMS[46].
Quand un amas d'étoiles est formé à peu près au même moment, la durée de vie de ses étoiles dépend de leurs masses. Les étoiles les plus massives quittent la séquence principale en premières, suivies en série, au fur et à mesure, par des étoiles de masses toujours décroissantes. Les étoiles évoluent donc dans l'ordre de leur position sur la séquence principale, en commençant par les plus massives en haut à gauche du diagramme HR. La position actuelle où ces étoiles quittent la séquence principale est appelé le point de retournement. En connaissant le temps de vie sur la séquence principale à cet endroit, il est possible d'estimer l'âge de l'amas[47].
Stade séquence principale[modifier | modifier le code]
| Symbole | Grandeur représentée |
|---|---|
| Énergie totale à produire sur la durée de vie de l'étoile | |
| Masse de l'étoile sur la séquence principale | |
| Luminosité de l'étoile sur la séquence principale | |
| Masse du soleil | |
| Luminosité du soleil | |
| Valeur estimée du temps de vie de l'étoile sur la séquence principale |
La quantité totale d'énergie qu'une étoile peut produire par fusion nucléaire de l'hydrogène est limitée par la quantité d'hydrogène initialement disponible dans le cœur. Pour une étoile en équilibre, l'énergie produite au cœur est égale à l'énergie rayonnée en surface. La durée de vie d'une étoile peut donc être estimée, en première approximation, comme le rapport entre l'énergie totale qu'elle peut produire par fusion[48] et sa luminosité (la quantité d'énergie qu'elle rayonne par unité de temps)[49] :
- la quantité d'hydrogène initialement disponible pour la fusion est proportionnelle à la masse de l'étoile : ;
- les étoiles de la séquence principale, dont la masse est entre 0,1 et 50 M☉[50], suivent une loi empirique de corrélation où la luminosité est proportionnelle à une puissance de la masse[51] : .
Ces deux rapports de proportionnalité associés donnent donc :
Le temps de vie d'une étoile sur la séquence principale peut alors être estimé à partir de l'évolution connue et prévue du Soleil : il a été sur la séquence principale pendant environ 4,5 milliards d'années, et la quittera pour devenir une géante rouge dans 6,5 milliards d'années[52], soit un temps de vie total sur la séquence principale approché de 1010 ans. D'où l'approximation[53] :
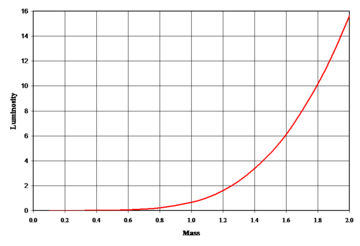
La puissance négative indique que le temps de vie sur la séquence principale de l'étoile varie en relation inverse avec sa masse. Une étoile sur la séquence principale est en première approximation une boule de gaz et de plasma dans laquelle la tendance à l’effondrement due à la gravité est contrebalancée par la tendance à l'inflation due à la pression de radiation. Pour une étoile massive, disposant de plus d'hydrogène à fusionner, cet équilibre est atteint pour une température du cœur nettement plus élevée, ce qui induit une vitesse de fusion très élevée : en quelque sorte, une étoile massive a un réservoir plus grand qu'une étoile de masse faible mais consomme beaucoup plus, elle a finalement une autonomie bien moindre.
Les étoiles les plus massives peuvent ainsi ne rester sur la séquence principale que quelques millions d'années, tandis que les étoiles de masse inférieure à 0,1 M☉ peuvent y rester plus de mille milliards (1012 années)[54].
Quand tout le combustible hydrogène du cœur a été consommé, l'étoile évolue en s'écartant de la séquence principale sur le diagramme HR. Le comportement d'une étoile dépend alors de sa masse : les étoiles de moins de 0,23 M☉ deviennent des naines blanches, tandis que celles ayant jusqu'à 10 M☉ passent par une étape de géante rouge[55]. Les étoiles plus massives peuvent exploser en supernova[56], ou s'effondrer directement en un trou noir.
Naine blanche[modifier | modifier le code]
Quand une étoile de la séquence principale a consommé l'hydrogène de son cœur, le ralentissement de la production d'énergie conduit l'effondrement gravitationnel à repartir. En ce qui concerne les étoiles de moins de 0,23 M☉[55], il est prévu qu'elles deviennent des naines blanches une fois que la production d'énergie par fusion nucléaire cessera, mais le processus est si lent qu'il leur faut plus que l'âge actuel de l'Univers.
Étoile géante[modifier | modifier le code]
Pour une étoile d'au moins 0,5 M☉[57], une fois que la réserve d'hydrogène dans le cœur est épuisée, elle gonfle pour devenir une géante, atteindre une température suffisante pour déclencher la fusion des noyaux d'hélium en carbone par le processus 3α[58],[59]. Les étoiles avec plus de 5–7,5 M☉ peuvent aussi fusionner des éléments de plus haut numéro atomique[60],[61].
La production d'énergie de cette voie par unité de masse n'est qu'un dixième de celle de l'hydrogène, et la luminosité de l'étoile s'accroît[36]. Ce stade de géante est plus bref que celui de la séquence principale : par exemple, le Soleil ne devrait rester que 130 millions d'années à ce stade, à comparer aux 10 milliards passés à fusionner l'hydrogène[62].
Géante rouge[modifier | modifier le code]
Dans les étoiles plus massives, jusqu'à 10 M☉, l'hydrogène entourant le cœur d'hélium atteint une température et une pression suffisantes pour subir la fusion, ce qui forme une couche de fusion de l'hydrogène. En conséquence, l'enveloppe externe de l'étoile se détend et se refroidit, et l'étoile devient une géante rouge. À ce point, l'étoile quitte donc la séquence principale et entre dans la branche des géantes. Elle suit une trajectoire d'évolution dans le diagramme de HR en diagonale opposée à la séquence principale, vers le haut à droite. C'est sa trajectoire d'évolution.
Le cœur d'hélium continue à se contracter, jusqu'à ce qu'il soit entièrement supporté par la pression de dégénérescence des électrons – un effet quantique qui limite la compression de la matière.
Supernova[modifier | modifier le code]
Pour les étoiles de 10 M☉ ou plus, ce processus pourrait conduire à un cœur toujours plus dense, qui finalement s'effondre, éjectant les couches externes en une explosion de supernova, de type II[56], de type Ib ou de type Ic.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Les lettres B et V désignent la magnitude d'une étoile vue à travers deux filtres colorés normalisés différents, « bleu » pour B et « visible » (vert-jaune) pour V. La différence montre dans quelle mesure la couleur s'éloigne du bleu.
- Pour les anglophones, une phrase mnémotechnique pour se rappeler la suite des types est « Oh Be A Fine Girl/Guy, Kiss Me ».
- Par définition. Le Soleil est une étoile de type G2 V typique.
- En mesurant la différence entre ces deux valeurs, on s'affranchit de la nécessité de connaître la distance de l'étoile. Cependant, voir extinction.
Références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Main sequence » (voir la liste des auteurs).
- (en) Harding E. Smith, « The Hertzsprung-Russell Diagram », Gene Smith's Astronomy Tutorial, Center for Astrophysics & Space Sciences, University of California, San Diego, (consulté le )
- (en) Richard Powell, « The Hertzsprung Russell Diagram », An Atlas of the Universe, (consulté le )
- (en) Malcolm S. Longair, The Cosmic Century : A History of Astrophysics and Cosmology, Cambridge, Cambridge University Press, , 545 p. (ISBN 0-521-47436-1).
- (Brown, Pais et Pippard 1995).
- (Russell 1913).
- Le paragraphe Nomenclature de cet article
- (en) Bengt Strömgren, « On the Interpretation of the Hertzsprung-Russell-Diagram », Zeitschrift für Astrophysik, vol. 7, , p. 222 – 248 (lire en ligne),
- (en) Évry L. Schatzman et Françoise Praderie, The Stars, Berlin/Heidelberg/Paris etc., Springer, , 402 p. (ISBN 3-540-54196-9, lire en ligne).
- (en) W. W. Morgan, P. C. Keenan et E. Kellman, An atlas of stellar spectra, with an outline of spectral classification, Chicago, Illinois, University of Chicago press, (lire en ligne).
- (Unsöld 1969).
- (en) George Gloeckler et Johannes Geiss, « Composition of the local interstellar medium as diagnosed with pickup ions », Advances in Space Research, vol. 34, no 1, , p. 53–60 (DOI 10.1016/j.asr.2003.02.054, lire en ligne)
- (en) Govert Schilling, « New Model Shows Sun Was a Hot Young Star », Science, vol. 293, no 5538, , p. 2188–2189 (PMID 11567116, DOI 10.1126/science.293.5538.2188, résumé).
- (Kroupa 2002).
- (Brainerd, 2005).
- (en) « Zero Age Main Sequence », The SAO Encyclopedia of Astronomy, Swinburne University (consulté le ).
- (Clayton 1983)
- paragraphe Trajectoires d'évolution de cet article
- (en) « Main Sequence Stars », Australia Telescope Outreach and Education (consulté le ).
- (en) Patrick Moore, The Amateur Astronomer, Springer, , 293 p. (ISBN 1-85233-878-4).
- (en) J. T. Wright, « Do We Know of Any Maunder Minimum Stars? », The Astronomical Journal, vol. 128, no 3, , p. 1273–1278 (DOI 10.1086/423221, lire en ligne).
- (en) Roger John Tayler, The Stars : Their Structure and Evolution, Cambridge University Press, , 241 p. (ISBN 0-521-45885-4, lire en ligne).
- (en) I. P. A. Sweet et A. E. Roy, « The structure of rotating stars », Monthly Notices of the Royal Astronomical Society, vol. 113, , p. 701–715 (lire en ligne).
- (en) Adam J. Burgasser, J. Davy Kirkpatrick et Sebastien Lépine, Proceedings of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, D. Reidel Publishing Co, Dordrecht, (ttp://adsabs.harvard.edu/cgi-bin/bib_query?arXiv:astro-ph/0409178), « Ultracool Subdwarfs: Metal-poor and Brown Dwarfs extending into the Late-type M, L and T Dwarfs », p. 237.
- (en) S. F. Green, Mark Henry Jones et S. Jocelyn Burnell, An Introduction to the Sun and Stars, Cambridge University Press, (ISBN 0-521-54622-2).
- (Karttunen 2003)
- (en) John N. Bahcall, M. H. Pinsonneault et Sarbani Basu, « Solar Models : Current Epoch and Time Dependences, Neutrinos, and Helioseismological Properties », The Astrophysical Journal, vol. 555, , p. 990–1012 (lire en ligne)Fig. 3, légende.
- (en) Maurizio Salaris et Santi Cassisi, Evolution of Stars and Stellar Populations, John Wiley and Sons, , 374 p. (ISBN 0-470-09220-3), p. 128.
- (en) M. S. Oey et C. J. Clarke, « Statistical Confirmation of a Stellar Upper Mass Limit », The Astrophysical Journal, vol. 620, no 1, , L43–L46 (lire en ligne).
- (en) Kenneth Ziebarth, « On the Upper Mass Limit for Main-Sequence Stars », Astrophysical Journal, vol. 162, , p. 947–962 (DOI 10.1086/150726, lire en ligne).
- (en) A. Burrows, W. B. Hubbard, D. Saumon et J. I. Lunine, « An expanded set of brown dwarf and very low mass star models », Astrophysical Journal, Part 1, vol. 406, no 1, , p. 158–171 (DOI 10.1086/172427, lire en ligne).
- (en) Lawrence H. Aller, Atoms, Stars, and Nebulae, Cambridge University Press, (ISBN 0-521-31040-7)
- (en) F. Martins, E. Depagne, D. Russeil et L. Mahy, « Evidence of quasi-chemically homogeneous evolution of massive stars up to solar metallicity », Astronomy & Astrophysics, vol. 554, , A23 (DOI 10.1051/0004-6361/201321282, Bibcode 2013A&A...554A..23M, arXiv 1304.3337).
- (en) A. G. Bressan, C. Chiosi et G. Bertelli, « Mass loss and overshooting in massive stars », Astronomy and Astrophysics, vol. 102, no 1, , p. 25–30 (lire en ligne).
- (en) Jim Lochner, Meredith Gibb, Phil Newman, « Stars », NASA, (consulté le )
- (en) James N. Imamura, « Mass-Luminosity Relationship », University of Oregon, (consulté le ).
- (Prialnik 2000).
- (Rolfs et Rodney 1988)
- (en) Martin V. Zombeck, Handbook of Space Astronomy and Astrophysics, Cambridge University Press, , 2e éd. (ISBN 0-521-34787-4, lire en ligne)
- (en) « SIMBAD Astronomical Database », Centre de Données astronomiques de Strasbourg (consulté le )
- (en) R. Earle Luck et Ulrike Heiter, « Stars within 15 Parsecs: Abundances for a Northern Sample », The Astronomical Journal, vol. 129, no 2, , p. 1063–1083 (DOI 10.1086/427250, lire en ligne)
- (en) « LTT 2151 High proper-motion Star », Centre de Données astronomiques de Strasbourg (consulté le )
- (en) « List of the Nearest Hundred Nearest Star Systems », Research Consortium on Nearby Stars, (consulté le )
- (en) « Origin of the Hertzsprung-Russell Diagram », University of Nebraska (consulté le ).
- (en) Lionel Siess, « Computation of Isochrones », Institut d'Astronomie et d'Astrophysique, Université libre de Bruxelles, (consulté le ) – Comparer par exemple les isochrones du modèle engendrées pour une ZAMS de 1 M☉. C'est listé dans la table comme 1,26 fois la luminosité solaire. À la métallicité de Z = 0,01 ; la luminosité est de 1,34 luminosité solaire. À la métallicité de Z = 0,04 ; la luminosité est de 0,89 luminosité solaire.
- (en) D. O. Gough, « Solar interior structure and luminosity variations », Solar Physics, vol. 74, , p. 21–34 (DOI 10.1007/BF00151270, lire en ligne).
- (en) Thanu Padmanabhan, Theoretical Astrophysics, Cambridge, Cambridge University Press, , 619 p. (ISBN 0-521-56241-4).
- (en) Lawrence M. Krauss et Brian Chaboyer, « Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology », Science, vol. 299, no 5603, , p. 65–69 (DOI 10.1126/science.1075631, résumé).
- (en) David Arnett, Supernovae and Nucleosynthesis : An Investigation of the History of Matter, from the Big Bang to the Present, Princeton University Press, (ISBN 0-691-01147-8). La fusion de l'hydrogène donne 8 × 1018 erg/g, tandis que celle de l'hélium ne donne que 8 × 1017 erg/g
- (en) Michael W. Richmond, « Stellar evolution on the main sequence », Rochester Institute of Technology, (consulté le )
- (Rolfs et Rodney 1988, p. 46)
- Pour une reconstruction historique détaillée de la démonstration théorique de cette relation par Eddington en 1924, voir (en) Stefano Lecchini, How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation, Bern Studies in the History and Philosophy of Science, , 228 p. (ISBN 978-3-9522882-6-9 et 3-9522882-6-8)
- (en) I.-Juliana Sackmann, Arnold I. Boothroyd et Kathleen E. Kraemer, « Our Sun. III. Present and Future », Astrophysical Journal, vol. 418, , p. 457–468 (DOI 10.1086/173407, lire en ligne)
- (en) Carl J. Hansen et Steven D. Kawaler, Stellar Interiors : Physical Principles, Structure, and Evolution, Birkhäuser, , 446 p. (ISBN 0-387-94138-X, lire en ligne), p. 28
- (en) Gregory Laughlin, Peter Bodenheimer et Fred C. Adams, « The End of the Main Sequence », The Astrophysical Journal, vol. 482, , p. 420-432 (DOI 10.1086/304125, lire en ligne)
- (Adams et Laughlin 1997)
- (Gilmore 2004)
- (en) Hans O. U. Fynbo, ISOLDE Coll. et al., « Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances », Nature, vol. 433, , p. 136–139 (DOI 10.1038/nature03219, résumé).
- (en) Michael L. Sitko, « Stellar Structure and Evolution », University of Cincinnati (consulté le )
- (en) « Post-Main Sequence Stars », Australia Telescope Outreach and Education (consulté le ).
- (en) L. Girardi, A. Bressan, G. Bertelli et C. Chiosi, « Evolutionary tracks and isochrones for low- and intermediate-mass stars: From 0.15 to 7M☉ , and from to 0.03 », Astronomy and Astrophysics Supplement, vol. 141, , p. 371–383 (DOI 10.1051/aas:2000126, lire en ligne).
- (en) A. J. T. Poelarends, F. Herwig, N. Langer et A. Heger, « The Supernova Channel of Super-AGB Stars », The Astrophysical Journal, vol. 675, no 1, , p. 614–625 (DOI 10.1086/520872, lire en ligne).
- (en) K.-P. Schröder et Robert Connon Smith, « Distant future of the Sun and Earth revisited », Monthly Notices of the Royal Astronomical Society, vol. 386, no 1, , p. 155–163 (DOI 10.1111/j.1365-2966.2008.13022.x, lire en ligne).
Sources[modifier | modifier le code]
- (en) Une simulation d'évolution dans le diagramme HR en fonction de la masse (moteur d'animation Java). Consulté le
- (en) Mitchell Charity, « What color are the stars? », Vendian Systems, (consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Fred C. Adams et Gregory Laughlin, « A Dying Universe: The Long Term Fate and Evolution of Astrophysical Objects », Reviews of Modern Physics, vol. 69, no 2, , p. 337–372 (DOI 10.1103/RevModPhys.69.337)
- (en) Jerome James Brainerd, « Main-Sequence Stars », The Astrophysics Spectator, (consulté le )
- (en) Laurie M. Brown, Abraham Pais et A. B. Pippard, Twentieth Century Physics, Bristol/Philadelphia/New York, CRC Press, (ISBN 0-7503-0310-7)
- (en) Donald D. Clayton, Principles of Stellar Evolution and Nucleosynthesis, University of Chicago Press, , 612 p. (ISBN 0-226-10953-4, lire en ligne)
- (en) Gerry Gilmore, « The Short Spectacular Life of a Superstar », Science, vol. 304, no 5697, , p. 1915–1916 (PMID 15218132, DOI 10.1126/science.1100370, lire en ligne)
- (en) Hannu Karttunen (trad. du finnois), Fundamental Astronomy, Berlin, Springer, , 468 p. (ISBN 3-540-00179-4)
- (en) Pavel Kroupa, « The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems », Science, vol. 295, no 5552, , p. 82–91 (résumé)
- (en) Dina Prialnik, An Introduction to the Theory of Stellar Structure and Evolution, Cambridge University Press, , 261 p. (ISBN 0-521-65937-X, lire en ligne)
- (en) Claus E. Rolfs et William S. Rodney, Cauldrons in the Cosmos : Nuclear Astrophysics, University of Chicago Press, (ISBN 0-226-72457-3)
- (en) H. N. Russell, « "Giant" and "dwarf" stars », The Observatory, vol. 36, , p. 324–329 (lire en ligne)
- (en) Albrecht Unsöld, The New Cosmos, Springer Verlag, , p. 268