Méthode des éléments finis
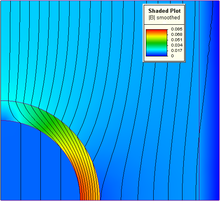
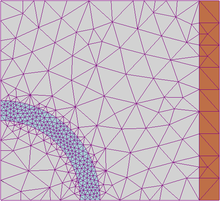

En analyse numérique, la méthode des éléments finis (MEF, ou FEM pour finite element method en anglais) est utilisée pour résoudre numériquement des équations aux dérivées partielles. Celles-ci peuvent par exemple représenter analytiquement le comportement dynamique de certains systèmes physiques (mécaniques, thermodynamiques, acoustiques, etc.).
Cette méthode permet par exemple de calculer numériquement le comportement d'objets même très complexes, à condition qu'ils soient continus et décrits par une équation aux dérivées partielles linéaire : mouvement d'une corde secouée par l'un de ses bouts, comportement d'un fluide arrivant à grande vitesse sur un obstacle, déformation d'une structure métallique, etc.
Description[modifier | modifier le code]
La méthode des éléments finis fait partie des outils de mathématiques appliquées. Il s'agit de mettre en place, à l'aide des principes hérités de la formulation variationnelle ou formulation faible, un algorithme discret mathématique permettant de rechercher une solution approchée d’une équation aux dérivées partielles (ou EDP) sur un domaine compact avec conditions aux bords et/ou dans l'intérieur du compact. On parle couramment de conditions de type Dirichlet (valeurs aux bords) ou Neumann (gradients aux bords) ou de Robin (relation gradient/valeurs sur le bord).
Il s'agit donc avant tout de la résolution approchée d'un problème, où, grâce à la formulation variationnelle, les solutions du problème vérifient des conditions d'existence plus faibles que celles des solutions du problème de départ et où une discrétisation permet de trouver une solution approchée. Comme de nombreuses autres méthodes numériques, outre l'algorithme de résolution en soi, se posent les questions de qualité de la discrétisation :
- existence de solutions ;
- unicité de la solution ;
- stabilité ;
- convergence ;
- mesure d'erreur entre une solution discrète et une solution unique du problème initial.
Historique[modifier | modifier le code]
La méthode des éléments finis est apparue avec l'analyse des structures, née vers 1940. Les premières études ont été menées sur la résistance des matériaux dans des conditions de petites déformations, ce qui a permis d'obtenir des systèmes simples résolus « manuellement », notamment par Maxwell[Lequel ?], Castigliano, Mohr. La formalisation, et le concept mathématique d'élément fini est apparu bien plus tard, vers 1950 et la définition est posée par Newmark, Hrennikoff, Mc Henry et Courant[1].
Le calcul numérique et les méthodes de résolution performantes par ordinateur ont permis de populariser la méthode, en offrant des possibilités d'hypothèses nombreuses et des apports probabilistes[2].
Cadre général[modifier | modifier le code]
Sont décrits ici le cadre général de la méthode des éléments finis, ainsi que le cas pratique le plus courant, considérant des équations aux dérivées partielles linéaires dont on cherche une approximation par des fonctions affines.
Principe général[modifier | modifier le code]
Considérons un domaine Ω (typiquement une portion de l'espace) dont la frontière est notée δΩ ou Σ. Nous cherchons à déterminer une fonction u définie sur Ω, qui est une solution d'une équation aux dérivées partielles (EDP) pour des conditions aux limites données. L'EDP décrit le comportement physique du système, il s'agit par exemple des lois de l'élasticité pour un problème de résistance des matériaux ou des équations de Maxwell pour les problèmes d'électromagnétisme. Les conditions aux limites sont les contraintes s'exerçant sur le système. Par exemple, pour un problème de résistance des matériaux, on impose le déplacement de certaines parties du système, par exemple, on impose qu'une zone d'appui soit immobile, et on impose des efforts sur d'autres zones (poids, pression de contact…).
La méthode des éléments finis (MEF) permet de résoudre de manière discrète et approchée ce problème ; on cherche une solution approchée « suffisamment » fiable.
La discrétisation consiste à « découper » le domaine Ω, c'est-à-dire à chercher une solution du problème sur un domaine polygonal ou polyédrique par morceaux ; il y a donc une redéfinition de la géométrie. Une fois la géométrie approchée, il faut choisir un espace d'approximation de la solution du problème. Dans la MEF, cet espace est défini à l'aide du maillage du domaine (ce qui explique aussi pourquoi il est nécessaire d'approcher la géométrie). Le maillage du domaine permet d'en définir un pavage dont les pavés sont les éléments finis.
Sur chacun des éléments finis, il est possible de linéariser l'EDP, c'est-à-dire de remplacer l'équation aux dérivées partielles par un système d'équations linéaires, par approximation. Ce système d'équations linéaires peut se décrire par une matrice ; il y a donc une matrice par élément fini. Cependant, les conditions aux frontières sont définies sur les frontières du système global et pas sur les frontières de chaque élément fini ; il est donc impossible de résoudre indépendamment chaque système. Les matrices sont donc réunies au sein d'une matrice globale. Le système d'équations linéaires global est résolu par l'ordinateur (des systèmes simples peuvent être résolus à la main et constituent en général des exercices d'apprentissage).
L'EDP est résolue aux nœuds du maillage, c'est-à-dire que la solution est calculée en des points donnés (résolution discrète) et non en chaque point du domaine Ω. Cela nécessite de pouvoir interpoler, c'est-à-dire déterminer les valeurs en tout point à partir des valeurs connues en certains points. On utilise en général des fonctions polynomiales. Un élément fini est la donnée d'une cellule élémentaire et de fonctions de base de l'espace d'approximation dont le support est l'élément, et définies de manière à être interpolantes (voir Fonctions de base).
Nous voyons ici poindre trois sources d'erreurs, c'est-à-dire d'écart entre la solution calculée et les valeurs réelles :
- la modélisation de la réalité : le domaine Ω correspond en général à des pièces matérielles, le calcul se fonde sur des versions idéales (sans défaut) des pièces, de la matière et des conditions aux limites ; cette source d'erreur n'est pas spécifique à la méthode des éléments finis, et peut être prise en compte par la méthode contrainte-résistance ;
- la géométrie idéale et continue est remplacée par une géométrie discrète, et les valeurs sont interpolées entre des points ; plus les points sont espacés, plus la fonction d'interpolation risque de s'écarter de la réalité, mais à l'inverse, un maillage trop fin conduit à des temps de calculs extrêmement longs et nécessite des ressources informatiques (en particulier mémoire vive) importantes, il faut donc trouver un compromis entre coût du calcul et précision des résultats ;
- s'agissant de calculs numériques, il se produit inévitablement des erreurs d'arrondi, les nombres étant représentés par un nombre fini d'octets.
Toute l'habileté de l'ingénieur consiste à maîtriser ces erreurs, notamment :
- en simplifiant la géométrie (defeaturing), en enlevant des détails qui se situent loin des zones que l'on veut étudier et ayant une faible influence sur le résultat ;
- en choisissant des maillages adaptés, par exemple, des maillages de type poutre pour des pièces élancées, ou de type coque pour des pièces fines, en découpant la pièce pour pouvoir faire des maillages réguliers sur certaines zones, en affinant le maillage dans les zones critiques…
- en ayant un regard critique sur le résultat.
Bien qu'il existe de nombreux logiciels exploitant cette méthode et permettant de « résoudre » des problèmes dans divers domaines, il est important que l'utilisateur ait une bonne idée de ce qu'il fait, notamment quant au choix du maillage et du type d'éléments qui doivent être adaptés au problème posé : aucun logiciel ne fait tout pour l'utilisateur, et il faut toujours garder un œil critique vis-à-vis de solutions approchées. Pour cela il existe des indicateurs d'erreur et des estimateurs d'erreur qui permettent d'ajuster les différents paramètres.[style à revoir]
La solution trouvée, il reste cependant à déterminer les caractéristiques de la méthode ainsi développée, notamment l'unicité de l'éventuelle solution ou encore la stabilité numérique du schéma de résolution. Il est essentiel de trouver une estimation juste de l'erreur liée à la discrétisation et montrer que la méthode ainsi écrite converge, c’est-à-dire que l'erreur tend vers 0 si la finesse du maillage tend elle aussi vers 0.
Dans le cas d'une EDP linéaire avec opérateur symétrique (comme l'est l'opérateur laplacien), il s'agit finalement de résoudre une équation algébrique linéaire, inversible dans le meilleur des cas.
Dimensions[modifier | modifier le code]
Pour l'explication, nous développons ici la méthode des éléments finis en deux dimensions à valeurs réelles. On suppose que les équations étudiées sont des équations différentielles d'ordre deux.
La méthode est généralisable à des cadres d'espaces de dimension différente ou pour des équations aux dérivées partielles d'ordre supérieur :
- on traite ici le cas d'une solution réelle à une EDP ; les cas où la dimension de la solution serait plus grande se traitent de façon similaire mais nécessitent des écritures plus complètes ; les cas les plus couramment rencontrés sont la dimension 1 (comme ici), 2 ou 3 (pour des problèmes de mécanique), 6 ou 12 (pour des problèmes d'électromagnétisme respectivement réels ou complexes) ;
- les degrés de différentiation supérieurs sont ramenés à un degré moindre par la méthode classique de réduction de degré : on fait intervenir des variables supplémentaires, c'est-à-dire des dérivées partielles des variables de départ (exemple classique : les EDP de la mécanique statique des poutres font intervenir la dérivation partielle d'ordre 4) ; il est parfois possible, pour des degrés supérieurs, d'appliquer plusieurs fois les méthodes de formulation variationnelle afin d'obtenir des ordres plus faibles — en tout cas lorsque le degré de dérivation est pair.
Bien que théoriquement la méthode soit transposable en dimensions supérieures du support, techniquement la complexité de création des discrétisations croît avec la dimension… et pratiquement, on résout rarement des problèmes en dimensions supérieures à 3 — y compris des problèmes de dynamique en espace à 3 dimensions qui pourraient être traités en quatre dimensions mais sont traités en réalité avec une méthode mixte éléments finis « en espace » et en différences finies « en temps ».
Cadre algébrique, analytique et topologique[modifier | modifier le code]
Soit un domaine (ouvert borné et connexe) Ω de , de bord δΩ, et d'adhérence (compacte) Ω. Pour simplifier les représentations, on suppose le bord polygonal.
Soient les fonctions de Ω dans différentiables sur Ω (compact) et deux fois différentiables sur Ω (ouvert). De telles fonctions sont continues et différentiables sur le bord du compact. Soit V(Ω) l'ensemble de ces fonctions (V est un espace vectoriel de dimension infinie et V0 est le sous-espace vectoriel de fonctions de V nulles sur le bord δΩ).
Soient les applications continues sur Ω et différentiables sur Ω, de carré sommables sur Ω et de gradient de carré sommable sur Ω (ou de dérivées partielles de carré sommable, ce qui revient au même avec le support de dimension finie). Nommons cet espace . Cet espace est un espace de Sobolev. On dote cet espace vectoriel d'un produit scalaire issu de celui de L2 tel que si (u, v) appartiennent à cet espace alors le produit scalaire de u et v est :
Le Théorème de la divergence (ou formule de Green-Ostrogradski) permet de retrouver le laplacien de u, donc la formulation variationnelle sous la forme initiale. On note le sous-espace vectoriel de dont les fonctions sont nulles sur le bord δΩ. L'opérateur est un produit scalaire sur l'espace
Cas organique[modifier | modifier le code]
Hypothèses[modifier | modifier le code]
On considère ƒ une fonction continue sur Ω de carré sommable et u la solution de l'équation aux dérivées partielles suivante sur Ω (Δ est l'opérateur laplacien) :
Avec la condition au bord u = 0 sur δΩ. Ceci peut également se réécrire u ∈ V0. Cette condition au bord s'appelle la condition de Dirichlet.
On démontre qu'il existe une solution unique à ce problème d'EDP à l'aide du théorème de Lax-Milgram.
Formulation faible[modifier | modifier le code]
Soit v ∈ V0 quelconque. Multiplions les deux parties de l'équation précédente par v puis sommons sur le domaine Ω, puisque v et ƒ sont tous deux de carré sommable sur ce domaine. On obtient l'équation :
On utilise pour le premier terme une intégration par parties[3] :
Dans cette formulation, v est nulle sur le bord (v ∈ V0) ce qui permet d'obtenir la formulation faible du problème :
Si u est deux fois différentiable, il y a équivalence entre cette formulation et celle du problème initial donné dans la section hypothèse et alors la solution de la formulation faible est la même que la solution initiale. On peut donc résoudre la formulation faible au lieu de résoudre le problème initial.
La question de savoir s'il y a équivalence entre la formulation faible et la formulation initiale donnée dans les hypothèses peut être particulièrement délicate dans les cas limites où l'ouvert Ω n'est pas suffisamment régulier (par exemple s'il y a des points singuliers) ou si ƒ n'est pas suffisamment dérivable (si l'on ne suppose pas que ƒ est au moins L2). Il faut alors souvent se ramener à une étude au cas par cas et rien ne dit que la formulation faible aura les mêmes solutions que l'équation de départ. Dans la majorité des problèmes physiques la solution est souvent et l'on ne se pose pas de tels problèmes. Néanmoins, pour des domaines avec des points singuliers cette équivalence peut poser problème. Ceci peut être gênant pour l'étude de fissures en mécanique des milieux continus par exemple.
Notations et cadre général[modifier | modifier le code]
Pour plus de généralité et pour rendre la suite plus lisible on utilisera les notations suivantes :
- avec a un opérateur bilinéaire symétrique (de V2 dans ) ;
- avec un opérateur linéaire (de V dans ).
On peut résoudre par la méthode des éléments finis toute équation aux dérivées partielles dont la forme faible se met sous la forme
On montre que a est un opérateur bilinéaire coercif continu selon la norme (voir Espace de Sobolev) et un opérateur linéaire continu également selon la norme . Avec ces notations, le problème se reformule ainsi :
Puisque k > 0, le théorème de Lax-Milgram assure l'existence de la solution et montre que u, solution du problème précédent, est la solution unique du problème d'optimisation de la fonctionnelle suivante :
Cette égalité peut avoir un sens physique notamment du point de vue de l'énergie pour certaines équations physiques et peut servir à montrer l'existence et l'unicité de la solution grâce aux propriétés de a et de (linéarité, coercivité, …).
Choix d'un maillage et discrétisation[modifier | modifier le code]
Choix d'un maillage[modifier | modifier le code]


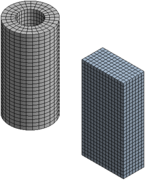
La méthode des éléments finis repose sur un découpage de l'espace selon un maillage. D'habitude l'on choisit un maillage carré ou triangulaire mais rien n'interdit de choisir des maillages plus complexes. Il n'est pas non plus nécessaire que le maillage soit régulier et l'on a tendance à resserrer le maillage près des endroits d'intérêt (par exemple aux endroits où l'on pense que la solution va beaucoup varier) ; cependant, il faut veiller à avoir des éléments faiblement distordus (se rapprocher d'un polygone régulier). Plus ce maillage est resserré, plus la solution que l'on obtient par la méthode des éléments finis sera précise et proche de la « vraie » solution de l'équation aux dérivés partielles.
On appelle traditionnellement h la plus grande dimension d'un élément (le diamètre de la sphère dans laquelle s'inscrit l'élément), et p le degré du polynôme décrivant le côté ou l'arête (p = 1 pour des côtés/arêtes droits, p = 2 pour des côtés/arête présentant une courbure).
Dans l'idéal, le maillage doit donc épouser les contours δΩ du domaine. Si δΩ est courbe, alors on peut :
- soit utiliser des éléments plus petits, on parle de raffinement de type h ;
- soit utiliser des éléments dont les côtés (en 2D) ou arêtes (en 3D) sont courbes, on parle de raffinement de type p.
Lorsque le degré des polynômes p est élevé, on parle de méthode des éléments spectraux.
Définition formelle[modifier | modifier le code]
Le cadre mathématique des éléments finis permet de poser un système assurant la bonne définition de la solution.
Élément fini — On appelle élément fini la donnée d'un triplet (K, PK, ΣK) avec
- K est un domaine géométrique,
- PK est un espace de fonctions sur K, qu'on appelle espace des fonctions de base,
- ΣK est un ensemble de formes linéaires sur PK, qu'on appelle degrés de liberté.
Cette définition offre a priori beaucoup de liberté, mais en général, plusieurs conditions sont imposées : le domaine K est pris comme non dégénéré, l'espace des fonctions de base sera choisi de dimension finie et simples à calculer et les degrés de liberté seront pris comme vérifiant la propriété d'unisolvance :
Unisolvance — L'élément fini (K, PK, ΣK) est dit unisolvant si les valeurs sur chaque degré de liberté permettent de spécifier une unique fonction de PK.
Fonctions de base[modifier | modifier le code]
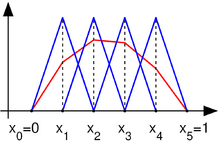
On doit après prendre une base de fonctions « adaptées » au maillage. Plusieurs choix sont alors possibles. En général, les fonctions de base utilisées pour les éléments finis sont interpolantes, c'est-à-dire que les valeurs nodales sont les valeurs des grandeurs inconnues aux nœuds.
La plus simple est l'emploi des polynômes de Lagrange. Dans cette méthode les fonctions de base valent 1 à un nœud du maillage et 0 à tous les autres. La fonction de base i est alors la fonction valant 1 au nœud i et 0 sur les autres nœuds et qui est polynomiale sur chaque élément. Un exemple de telles fonctions est représenté en dimension 1 à côté. Il y a autant de fonctions de base par élément que de nombre de nœuds.
On appelle « élément » la donnée d'une géométrie (souvent polygonale en 2D, polyédrique en 3D) et de fonctions de base associées à cette géométrie.
D'autres solutions peuvent exister pour les fonctions de base. On cite ici un seul exemple les éléments finis d'Hermite qui ont la particularité d'avoir deux fonctions de base associées à chaque nœud. Dans cette version, la valeur de la solution est ajustée avec la première fonction alors que la deuxième permet d'ajuster la valeur de la dérivée. Ce type de fonctions de base peut avoir un intérêt pour la résolution de certaines équations aux dérivées partielles (par exemple l'équation des plaques en mécanique des milieux continus), même si elle nécessite d'avoir deux fois plus de fonctions pour un maillage donné.
Quelques éléments classiques[modifier | modifier le code]

En 2D :
- triangles :
- triangles de degré 1 (triangles à 3 nœuds, fonctions linéaires),
- triangles de degré 2 (triangles à 6 nœuds, polynômes de degré 2) ;
- quadrilatères :
- quadrilatères de degré 1 (carrés à quatre nœuds, fonctions linéaires),
- quadrilatères de degré 2 (carrés à 8 ou 9 nœuds, polynômes de degré 2).
En 3D :
- tétraèdres :
- hexaèdres[6] :
- hexaèdres de degré 1 (huit nœuds, fonctions linéaires),
- hexaèdres de degré 2 (vingt nœuds, polynômes de degré 2),
- hexaèdres triquadratiques (vingt-sept nœuds, polynômes de degré 2).

Discrétisation[modifier | modifier le code]
Soit le maillage et la base associée. Puisque la condition de Dirichlet impose des fonctions nulles aux bords, on utilise uniquement la sous-base limitée aux points intérieurs de .
On cherche la solution du problème discrétisé ainsi :
Or dans cet espace discrétisé, dire que tout vecteur vérifie la proposition précédente est équivalent à dire que tous les vecteurs de la base vérifient la proposition. Si l'on décompose la solution dans la base des intérieurs, en composantes , on obtient :
L'idée est que quand le maillage se resserre et que le nombre de fonctions de base tend vers l'infini (et que l'espace engendré par cette base croit vers ), les solutions devront converger vers la solution de l'équation aux dérivées partielles de départ.
Éventuelle deuxième discrétisation[modifier | modifier le code]
Dans certains problèmes physiques, il peut être intéressant de discrétiser une deuxième fois. Cette seconde discrétisation n'est pas nécessaire pour la méthode des éléments finis. Souvent on a comme expression de :
On projette alors f sur la base b. On obtient :
et on approche par
Le problème est d'obtenir ensuite une projection acceptable sachant qu'il n'y a pas nécessairement de produit scalaire associé à la base qui permette de projeter de façon efficace. Dans les deux exemples de bases donnés plus haut, cette projection est aisée. Dans le cas des éléments finis de Lagrange, la projection sur la fonction ei est donnée par la valeur en xi ; dans le cas des éléments d'Hermite, c'est la valeur de la fonction ainsi que de sa dérivée qui permettent d'obtenir la projection. Pour d'autres bases, la projection peut être plus compliquée.
Problème sous forme matricielle[modifier | modifier le code]
Si l'on note :
- la matrice A ayant pour composantes les a(ei, ej) ;
- le vecteur U ayant pour composantes les ui qui sont les coordonnées de la solution approchée sur la base b ;
- le vecteur ayant pour composantes les ;
alors ce problème revient à résoudre l'équation linéaire de n équations à n inconnues :
La matrice est appelée matrice de rigidité par analogie avec certains problèmes de mécanique des solides. A est par construction symétrique, et puisque a est coercive, alors A est symétrique, définie positive donc inversible. On obtient donc l'existence et l'unicité de U = A−1B. Grâce aux coordonnées de u sur la base b on peut alors construire la solution approchée u. Quand le maillage se resserre cette solution approchée va tendre vers la vraie solution de l'équation aux dérivées partielles de départ.
Pour le cas avec une deuxième discrétisation de on obtient :
où M est appelée la matrice de masse et contient les . f est un vecteur contenant les coordonnées de f dans la base. La méthode est alors la même qu'avec une seule discrétisation puisque A vérifie les mêmes propriétés. Cette méthode peut parfois être préférée quand on peut obtenir de façon simple la projection de f sur la base et la matrice M.
Algorithme[modifier | modifier le code]
La méthode des éléments finis doit être conduite ainsi :
- On calcule la matrice de rigidité A ;
- On détermine le membre de droite, en calculant les termes ou alors par l'intermédiaire de la matrice de masse ;
- On résout le problème AU=B ou le problème AU=Mf suivant le niveau de discrétisation choisi. U est alors donné par . Selon la base qui a été choisie et selon les données du problème, il faut choisir la méthode d'inversion la plus efficace pour A. C'est l'étape la plus consommatrice en puissance de calcul, et l'efficacité de la méthode en termes de temps de calcul se joue principalement sur cette étape ;
- On peut écrire grâce au vecteur U qui contient les coordonnées de sur la base b et obtenir une solution approchée au problème.
Condition de Neumann[modifier | modifier le code]
La condition qui suit est très différente de celle de Dirichlet. On pose comme condition au bord que la dérivée normale existe sur le bord , et que la condition de Neumann est vérifiée.
Si la fonction est supposée différentiable au bord , voire si elle admet un gradient .
Le résultat fonctionne de la même manière car l'élément clef de la démonstration où intervient l'hypothèse de bord est que l'intégrale parce que cette fois-ci ce n'est pas la fonction test mais la dérivée normale qui est nulle.
Par la suite, la différence réside surtout dans le choix des vecteurs de base pour la discrétisation : il faut conserver les fonctions tests propres aux nœuds du bord.
Exemples issus de problèmes physiques[modifier | modifier le code]
Sont présentés ici des exemples essentiellement de physique, notamment de mécanique. Ils apportent un biais certain quant à une approche plus générale, du fait notamment de la linéarité supposée des matériaux.
Exemple de problème discret : un réseau électrique[modifier | modifier le code]

Équation locale du composant e :
soit
On écrit :
- la continuité des potentiels en chaque connexion ;
- l'équilibre des courants à chaque connexion ;
- l'adjonction des courants externes .
On obtient l'équation globale du système assemblé :
soit :
Définition d'un élément fini[modifier | modifier le code]


En calcul de structures, un élément fini est caractérisé par deux matrices :
- la matrice de raideur ;
- la matrice de masse .
Application de la méthode des éléments finis à la mécanique[modifier | modifier le code]
Définitions et notations[modifier | modifier le code]
On cherche ici à déterminer le vecteur des déplacements C'est un vecteur dont chaque composante est également appelée degré de liberté (ddl) :
- 3 ddl de translation : ;
- 3 ddl de rotation : .
On écrit alors le tenseur des déformations , qui modélise la façon dont le matériau va se déformer par rapport à sa position initiale.
Sous l'hypothèse des petites déformations, on a

Comme , on a
Sous l'hypothèse des petites déformations, on néglige les termes d'ordre 2 :
Remarque : est sans dimension.
On écrit ensuite le tenseur des contraintes) , qui représente les efforts internes qui s'appliquent dans la structure.
- : contraintes normales.
- : contraintes de cisaillement.
Une contrainte est homogène à une pression (N/m²).
Ces deux tenseurs sont liés par une loi de comportement. On considère la loi de Hooke :
avec
- : module de Young (N/m²)
- : coefficient de Poisson (sans dimension)
On utilise parfois le module de cisaillement :
Pour un matériau isotrope, il n'y a que deux paramètres indépendants. Il y en a 6 pour un matériau isotrope transverse, 9 pour un matériau orthotrope et 21 pour un matériau anisotrope.
En notation matricielle, on écrit :
- est appelée matrice d'élasticité du matériau.
L'énergie de déformation W s'écrit
Travail d'une force
- Le travail d'une force est le produit de la force par le déplacement de son point d'application :
- Moment
- Le moment d'une force est la mesure d'une action entraînant une rotation, proportionnelle à la force et à la longueur du bras de levier entre le centre de rotation du solide et le point d'application de la force.
Équations fondamentales[modifier | modifier le code]
Équations d'équilibre local
Relations déformations-déplacements
- Symboliquement, on écrit

Si on applique au barreau une contrainte , on observe un rétrécissement dans la direction y correspondant à une déformation
Exemple de formulation : barre en traction[modifier | modifier le code]

On suppose que le déplacement en tout point de la barre est donné par un polynôme du 1er degré :
- On a et
- d'où
qu'on écrit symboliquement : avec
On en déduit :
D'autre part, on a par définition :
- où S est l'aire de la section de la barre.
On pose :
On obtient finalement :
Soit une relation du type :
En explicitant :
On voit que la matrice de rigidité se calcule comme le produit de trois matrices :
- : Transformation des déplacements aux déformations
- : Matrice d'élasticité du matériau
- : Transformation des contraintes en forces
Formulation générale (méthode directe)[modifier | modifier le code]
La démarche est la suivante :
- On exprime le déplacement en tout point de l'élément en fonction des déplacements aux nœuds ;
- On exprime les déformations en fonction des déplacements d'où
On écrit la loi de comportement du matériau qui relie les contraintes aux déformations :
On écrit que le travail des forces externes appliquées à la structure pour un déplacement virtuel est égal au travail interne des contraintes pour ce même déplacement :
En explicitant, on a :
Comme cette relation est vraie pour tout déplacement virtuel, on en déduit :
avec sous sa forme plus générale :
Remarques
- La relation ci-dessus montre que est symétrique.
- Le terme courant de la matrice correspond à la force qui s'exerce sur le nœud lorsqu'on impose un déplacement unitaire du nœud .
La symétrie de qui s'écrit correspond mécaniquement au théorème de réciprocité de Maxwell-Betti.
Les types d'éléments finis sont différenciés par le choix des fonctions N(x) et la nature de l'opérateur S (reliant déformations et déplacements), qui dépend du type de théorie élastique utilisée : théorie des poutres, théorie des plaques, théorie de la contrainte ou de la déformation plane, théorie des coques, théorie des corps de révolution, théorie de l'élasticité 3D.
Remarques Le processus de formulation d'un élément fini décrit ici est celui de la méthode directe (dite aussi méthode des déplacements). Il existe d'autres approches : la méthode des résidus pondérés, l'application du Principe des travaux virtuels ou des puissances virtuelles, et la minimisation de l'énergie potentielle. Ces approches sont équivalentes et aboutissent à la construction de la même matrice de rigidité.
Éléments finis en contrainte[modifier | modifier le code]
Au lieu de rechercher une solution approchée en déplacement, on peut aussi rechercher la solution approchée en contrainte.
Dans le cas de la mécanique, l'application du principe des puissances virtuelles donne de manière non triviale les théorèmes énergétiques. On peut aboutir au même résultat en quelques lignes en écrivant l'erreur en relation de comportement.
L'approche en contrainte consiste à rechercher dans l'espace des champs de contraintes admissibles celui qui réalise le minimum de l'énergie complémentaire.
Cette approche est plus précise que l'approche en déplacement mais elle est peu développée du fait de la difficulté que l'on a à générer des champs de contraintes de divergence donnée.
Étude des fonctions N(x)[modifier | modifier le code]
- Dans le cas général de l'élasticité tridimensionnelle, ce sont en fait des fonctions de x, y, z.
- Les fonctions les plus couramment utilisées sont des polynômes.
- Polynôme de degré 1 : élément linéaire (2 nœuds par arête)
- Polynôme de degré 2 : élément parabolique (3 nœuds par arête)
- Polynôme de degré 3 : élément cubique (4 nœuds par arête)
Les fonctions N(x) sont appelées fonctions de forme ou fonctions d'interpolation de l'élément.
Éléments isoparamétriques[modifier | modifier le code]
Il arrive alors un dilemme : soit on construit pour certains éléments de forme et de géométrie figée, et il est alors nécessaire, pour mailler une structure complexe, d'utiliser un grand nombre d'éléments, soit on utilise des éléments à géométries variables, et il faut reconstruire à chaque fois.
Une solution courante est alors d'utiliser des fonctions d'interpolation pour décrire non seulement le champ de déplacement de l'élément, mais également sa géométrie, tout en travaillant en coordonnées locales.
Interpolation de la géométrie[modifier | modifier le code]
Idem pour les autres coordonnées. |

|
Coordonnées locales (cas 2D)[modifier | modifier le code]
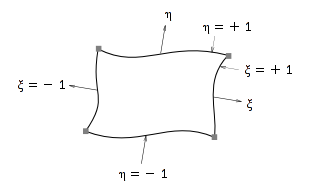
Élément isoparamétrique[modifier | modifier le code]
Un élément est dit isoparamétrique si on prend les mêmes fonctions d'interpolation pour le déplacement et la géométrie.
Autres classes d'éléments[modifier | modifier le code]

Évaluation de K[modifier | modifier le code]
La forme générale s'écrit :
On passe en variables locales
On a , où est la matrice jacobienne.
On est alors amené à calculer des intégrales du type :
Bénéfice de l'approche[modifier | modifier le code]
On s'est ramené à un domaine d'intégration simple et invariant pour lequel on peut appliquer les formules de quadrature de Gauss :
les et étant tabulés.
Les sont appelés points d'intégration de l'élément ou encore points de Gauss de l'élément.
Cas particulier : les éléments axisymétriques[modifier | modifier le code]

Décomposition en série de Fourier :
L'axisymétrie correspond à la restriction de cette décomposition.
Remarque Pour utiliser ce type d'élément, le problème doit être globalement axisymétrique en ce qui concerne la géométrie, les conditions limites et le chargement.
Processus de calcul (cas statique)[modifier | modifier le code]
- Maillage
- Construction de la matrice de raideur de chaque élément
- Assemblage de la matrice globale
- Construction du vecteur chargement
- Élimination de certains ddl (si besoin)
- Résolution :
- Calcul des quantités dérivées de
Logiciels de calcul aux éléments finis[modifier | modifier le code]
Quelques exemples de logiciels utilisant la méthode des éléments finis en mécanique des structures :
- ABAQUS : logiciel pluridisciplinaire développé par la société Dassault Systèmes
- ACORD : logiciel de calcul pour poutres et coques avec vérifications réglementaires selon Eurocodes (1, 2, 3, 5, 8) développé par la société ITECH
- Analysis3D : logiciel pluridisciplinaire libre développé par Cuylaerts Engineering[7].
- ANSYS : logiciel pluridisciplinaire développé par ANSYS
- Calculix : logiciel libre de calcul pour la 3D utilisé, par exemple, par le logiciel libre de conception FreeCAD[8].
- CAST3M : logiciel pluridisciplinaire français développé par le CEA (gratuit pour l'enseignement et la recherche)
- CESAR : logiciel de calcul des ouvrages du Génie Civil, développé par l'IFSTTAR (ex. Laboratoire Central des Ponts et Chaussées) et la société itech.
- Code_Aster : logiciel pluridisciplinaire libre français développé par EDF
- COMSOL Multiphysics : logiciel pluridisciplinaire développé par Comsol,
- EuroPlexus : logiciel français
- Flux : logiciel de CAO 2D&3D éléments finis (développé en collaboration avec le G2Elab) permettant le calcul des états magnétiques, électriques ou thermiques des dispositifs
- FreeFem++ : logiciel pluridisciplinaire libre.
- Feel++ : logiciel pluridisciplinaire libre.
- ICAB : logiciel de calcul pour poutres et coques avec vérifications réglementaires selon Document technique unifié DTU France (NV65, CM66, AL76, CB71...), Eurocodes, AISC américain
- Simcenter 3D : logiciel pluridisciplinaire developpé par la société Siemens Industry Software anciennement Siemens PLM Software
- XLiFE++ : logiciel pluridisciplinaire libre[9]
- Z-set/ZéBuLon : logiciel commercial de calcul non-linéaire avec lois matériaux complexes développé par l'ONERA/Safran Tech/Mines ParisTech pour la recherche.
Notes et références[modifier | modifier le code]
- J. S. Przemieniecki, Theory of matrix structural analysis, New York, McGraw-Hill Book Company, .
- Pierre-Alain Boucard, François Hild et Jean Lemaître, Résistance mécanique des matériaux et des structures - Introduction, Malakoff, Dunod, (ISBN 978-2-10-081475-6).
- Pour certains cas limites lorsqu'il n'y a pas suffisamment de régularité et que l'intégration par parties n'a pas de sens on utilise aussi une formulation adaptée du théorème de Stokes mais il faut alors définir la dérivée faible puis la divergence faible, ce qui entraine des complications supplémentaires.
- (en) Advanced Finite Element Methods, University of Colorado at Boulder, (lire en ligne [PDF]), « The Linear Tetrahedron ».
- (en) Advanced Finite Element Methods, University of Colorado at Boulder, (lire en ligne [PDF]), « The Quadratic Tetrahedron ».
- (en) Advanced Finite Element Methods, University of Colorado at Boulder, (lire en ligne [PDF]), « Hexahedron Elements ».
- [1].
- FreeCAD utilise Calculix
- B. Riou, « Welcome to XLiFE++’s website! », sur xlifepp.pages.math.cnrs.fr, (consulté le ).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Calcul de structures et modélisation
- NAFEMS
- Méthode des différences finies
- Méthode des volumes finis
- Méthode des éléments finis de frontière
- Théorème de Lax-Milgram
- Méthode des éléments discrets
- Méthode des éléments finis étendus
- Méthode de discrétisation du gradient
- Méthode sans maillage
- Analyse isogéométrique
- Formulation implicite ou explicite d'un problème de dynamique
- Éléments d'Argyris
Bibliographie[modifier | modifier le code]
- (en) G. Allaire and A. Craig, Numerical Analysis and Optimization:An Introduction to Mathematical Modelling and Numerical Simulation
- (en) K. J. Bathe, Numerical methods in finite element analysis, Prentice-Hall, 1976 (ISBN 0136271901)
- (en) P.G. Ciarlet, The Finite Element Method for Elliptic Problems, série « Studies in Mathematics and its Applications », North-Holland, Amsterdam, 1978 (ISBN 9780444850287).
- R. H. Gallagher, Introduction aux éléments finis, Pluralis, 1977
- P.A. Raviart et J.M. Thomas, Introduction à l'analyse numérique des équations aux dérivées partielles, Dunod, 2004 (ISBN 9782100486458).
- (en) O. C. Zienkiewicz, R. L. Taylor, J. Z. Zhu, The Finite Element Method: Its Basis and Fundamentals, Butterworth-Heinemann ; 6e édition () (ISBN 0750663200)
- (en) Kenneth H. Huebner, The Finite Element Method for Engineers, Wiley, (ISBN 978-0-471-37078-9) : une présentation claire, pratique et détaillée de la méthode des éléments finis, assortie de nombreux exemples résolus.
Liens externes[modifier | modifier le code]
- Josselin Delmas, Code_Aster: Fonctions de Forme et points d'intégration des éléments finis
- (en) La méthode des éléments finis en génie biomedicale et en biomécanique
- Hervé Oudin, Méthode des éléments finis, École centrale de Nantes
- Vincent Manet, La Méthode des Éléments Finis : vulgarisation des aspects mathématiques, illustration des capacités de la méthode
- David Dureisseix, Méthodes numériques appliquées à la conception par éléments finis, université Montpellier II - Sciences et Techniques du Languedoc
- Christian Wielgosz, Bernard Peseux, Yves Lecointe, Formulations mathématiques et résolution numérique en mécanique, université de Nantes





























![{\displaystyle \forall j\in [\![1,n]\!],\ \sum _{i=1}^{n}{u_{i}a(e_{i},e_{j})}={\mathcal {L}}(e_{j})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/022d2cf6cc62d476b5ba72672e0683bf2737a817)






















![{\displaystyle \left\{I^{e}\right\}=\left[K^{e}\right]\left\{U^{e}\right\}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2aa4d849b4a84ce2d3cd744ac12a998a3d3605b2)



![{\displaystyle \left\{P\right\}=\left[K\right]\left\{U\right\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b2cd3c16aab6c332a7ba09b502e65b301d20a00)
![{\displaystyle \left[K\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ccd71821e8c8f2792a84868e4e9345e5a25dafe)
![{\displaystyle \left[M\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e59ef4f5b349081755f6bf3a68e64b6208b14e31)



![{\displaystyle \left[\epsilon \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5003ea241fcfa980236cd065ec076c0a9c69f6d)







![{\displaystyle \left[\sigma \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51896ef77dc8075399169d80e74f8deb85d26180)






![{\displaystyle \left\{\sigma \right\}=\left[D\right]\left\{\epsilon \right\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1798ccc24501577fc6b11098fc231ca2eb613922)
![{\displaystyle \left[D\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9dc556f28e18658843e4b9728a107fcac4ca328)









![{\displaystyle \{\epsilon \}=[S]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97534d7a12b358e2a1aef1fc83c7709a0da96f91)






![{\displaystyle u(x)=[N(x)]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d043a744e8d22784d814d6f91a47acfaef8a3634)
![{\displaystyle \left|{\begin{matrix}[N(x)]&=&\left[\left(1-{x \over L}\right);\left({x \over L}\right)\right]\\\{U\}&=&{\begin{Bmatrix}u_{1}\\u_{2}\end{Bmatrix}}\end{matrix}}\right.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7a004ca22036168f97365198d59d4fdd34e453d)
![{\displaystyle \epsilon =\left[-{1 \over L};{1 \over L}\right]{\begin{Bmatrix}u_{1}\\u_{2}\end{Bmatrix}}=[B]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31834c58fddef8f28d8f2d81faaaf6d595a61d92)
![{\displaystyle \sigma =E\left[-{1 \over L};{1 \over L}\right]{\begin{Bmatrix}u_{1}\\u_{2}\end{Bmatrix}}=[D]\epsilon \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6459c329d95654edd8e2005c32242f0d435da499)

![{\displaystyle \{F\}={\begin{Bmatrix}F_{1}\\F_{2}\end{Bmatrix}}=[A]\sigma \qquad {\mbox{avec}}\qquad \{A\}=S{\begin{Bmatrix}-1\\1\end{Bmatrix}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44c7e79d12d9bc9212cec84780d983746fe022b4)
![{\displaystyle \{F\}=[A][D][B]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a4ce56fead6f1e03f1d5a102703b37256341bce)
![{\displaystyle \{F\}=[K]\{U\}\qquad {\mbox{avec}}\qquad [K]=[A][D][B]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d52cb698c9d173cc07aba8b47cd64288a44a02ab)
![{\displaystyle [K]={ES \over L}{\begin{bmatrix}1&-1\\-1&1\end{bmatrix}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5658dc1a653d787535f963b2c9d5c7d1672fe9f2)
![{\displaystyle [B]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c69e183a615e7bae607d746d3b7d44b0d8316ff6)
![{\displaystyle [D]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dc427a5347790db895210446aecc67ff70a7550)
![{\displaystyle [A]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cbf1fb4a9d38c91451b02e34253a0924d53addb)

![{\displaystyle \{u(x)\}=[N(x)]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ee2652e5645e977719d8efa1209c5c57308ed2f)
![{\displaystyle \{\epsilon (x)\}=[S]\{u(x)\},\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0906a815fd9bde383c1777301efedfd872412238)
![{\displaystyle \{\epsilon (x)\}=[S]\{N(x)\}\{U\}=[B(x)]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fc1e46db77576cd0422f87adbbda693f09aff4f)
![{\displaystyle \{\sigma (x)\}=[D]\{\epsilon (x)\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8400143a8c6218ae0be0a876b772af7317737c5b)


![{\displaystyle \{\delta U\}^{T}\{F\}=\{\delta U\}^{T}\left(\int _{V}[B]^{T}[D][B]\,\mathrm {d} v\right)\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82ac7d139c22036be968ae9c62d3f2e66e0baeba)
![{\displaystyle \{F\}=[K]\{U\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21a6df5acc424fddbd7f1c588789fb9cb401895)
![{\displaystyle [K]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b0e8fab19a5ebe75bfc8752a0a9ddd546a35833)
![{\displaystyle [K]=\int _{V}[B]^{T}[D][B]\,\mathrm {d} v\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348061b3ad069de0ba59daad41cde3bfa8c803a0)





![{\displaystyle [K]=\int _{x}\int _{y}\int _{z}G(x,y,z)\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c2f7b96bface0437f35c83a397a9b688c64c36)










![{\displaystyle [K^{e}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54a1c359729bde9fb7b1a9c9e2e82bcb2805e15)

![{\displaystyle \{U\}=[K^{-1}]\{F\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e703db6865d4cb5abc1a2f886c852adceebfad)

![{\displaystyle \{\epsilon ^{e}\}=[B^{e}]\{U^{e}\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38f59aff666377f3fa6901d54d88290157e15c91)
![{\displaystyle \{\sigma ^{e}\}=[D^{e}]\{\epsilon ^{e}\}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec2df66ba1a5761cf59483d916c57ee01645f42)
