Théorie des poutres
La théorie des poutres est un modèle utilisé dans le domaine de la résistance des matériaux. On utilise deux modèles :
- la théorie d'Euler-Bernoulli, qui néglige l'influence du cisaillement ;
- la théorie de Timoshenko qui prend en compte l'effet du cisaillement.
Le terme de « poutre » désigne un objet dont la longueur est grande par rapport aux dimensions transverses (section fine). Stricto sensu, une poutre est un élément de structure utilisé pour la construction dans les bâtiments, les navires et autres véhicules, et dans la fabrication de machines. Cependant, le modèle des poutres peut être utilisé pour des pièces très diverses à condition qu'elles respectent certaines conditions.
Historique[modifier | modifier le code]
La paternité de la théorie des poutres est attribuée à Galilée, mais des études récentes indiquent que Léonard de Vinci l'aurait précédé. Ce dernier avait supposé que la déformation variait de manière linéaire en s'éloignant de la surface neutre, le coefficient de proportionnalité étant la courbure, mais il ne put finaliser ses calculs car il n'avait pas imaginé la loi de Hooke. De son côté, Galilée était parti sur une hypothèse incorrecte (il supposait que la contrainte était répartie uniformément en flexion), et c'est Antoine Parent qui obtint la distribution correcte[1].
Ce sont Leonhard Euler et Jacques Bernoulli qui émirent la première théorie utile vers 1750, tandis que Daniel Bernoulli, le neveu du précédent, écrivit l'équation différentielle pour l'analyse vibratoire[2]. À cette époque, le génie mécanique n'était pas considéré comme une science, et l'on ne considérait pas que les travaux d'une académie des mathématiques puissent avoir des applications pratiques, et l'on continua à bâtir les ponts et les bâtiments de manière empirique. Ce n'est qu'au XIXe siècle, avec la Tour Eiffel et les grandes roues, que l'on démontra la validité de la théorie à grande échelle.
Principes de modélisation[modifier | modifier le code]
Démarche[modifier | modifier le code]

Pour étudier les poutres, on met en relation :
- les efforts de cohésion avec les efforts extérieurs, grâce au principe de la coupure ;
- les efforts de cohésion avec le tenseur des contraintes, grâce au principe d'équivalence ;
- le tenseur des contraintes avec le tenseur des déformations, grâce à la loi de Hooke généralisée ;
- et la forme finale de la poutre, c'est-à-dire le champ des déplacements, avec le champ de tenseur des déformations.
Le modèle de poutre permet de passer des efforts de cohésion au tenseur des contraintes ; il permet d'appliquer le principe d'équivalence.
Modèle de la poutre[modifier | modifier le code]


On appelle « poutre » un solide engendré par des surfaces finies, appelées « sections droites », telles que :
- l'ensemble des centres de gravité des sections droites est une courbe continue et différentiable, appelée « courbe moyenne » ; son rayon de courbure est grand devant sa longueur ;
- les sections droites sont perpendiculaires à la courbe moyenne ; elles « varient de manière continue et lente » ;
- la racine carrée de la surface des sections droites est petite devant la longueur de la courbe moyenne ;
- le matériau est homogène et isotrope.
Si le rayon de courbure est faible ou que la section varie brutalement, il faudra considérer les concentrations de contrainte.
Dans les cas les plus simples, notamment celui des poutres au sens « élément de structure » (fer, tube, etc.) la courbe moyenne est droite et les sections droites sont identiques.
Mais on peut modéliser d'autres types de pièces. Par exemple, un arbre de transmission, un axe, un levier, un tuyau, un réservoir, ou même la coque d'un navire peuvent être modélisés par une poutre ; un ressort hélicoïdal (ressort à boudin) peut être considéré comme une poutre dont la courbe moyenne est hélicoïdale, et dont les sections droites sont des disques de même rayon.
On appelle « fibre » un volume généré par une petite portion d²S de la section droite suivant une courbe parallèle à la courbe moyenne. On appelle « fibre neutre » la fibre générée par la courbe moyenne elle-même.
Pour simplifier, sauf indication contraire, nous dessinerons des poutres dont la courbe moyenne est une droite avant déformation.

Finalement, l'étape de modélisation consiste à :
- d'une part considérer la fibre neutre seule, caractérisée par sa longueur L (et si la poutre n'est pas droite, par une fonction y(x)) ;
- d'autre part à considérer les sections droites, caractérisées par leur aire S (pour la traction-compression) et leurs moments quadratiques IG (pour la torsion), IGy et IGz (pour la flexion).
Hypothèses pour les calculs[modifier | modifier le code]

pour les grandes déformations (bas), les hypothèses ne sont plus respectées, les sections droites deviennent gauches et ne sont plus perpendiculaires à la courbe moyenne.
La théorie des poutres est une application de la théorie de l'élasticité isotrope. Pour mener les calculs de résistance des matériaux, on considère les hypothèses suivantes :
- hypothèse de Bernoulli : au cours de la déformation, les sections droites restent perpendiculaires à la courbe moyenne ;
- les sections droites restent planes selon Navier-Bernoulli (pas de gauchissement).
L'hypothèse de Bernoulli permet de négliger le cisaillement dans le cas de la flexion : le risque de rupture est alors dû à l'extension des fibres situées à l'extérieur de la flexion, et la flèche est due au moment fléchissant. Cette hypothèse n'est pas valable pour les poutres courtes car ces dernières sont hors des limites de validité du modèle de poutre, à savoir que la dimension des sections doit être petite devant la longueur de la courbe moyenne. Le cisaillement est pris en compte dans le modèle de Timoshenko et Mindlin.
Calculs de résistance et de déformée[modifier | modifier le code]
Le but est de déterminer pour chaque point :
- le tenseur des contraintes afin de vérifier qu'il n'y a pas rupture (état limite ultime, ELU) ;
- la déformée finale, afin de vérifier que la poutre garde des dimensions compatibles avec son utilisation (état limite en service, ELS).
Efforts de cohésion[modifier | modifier le code]

Pour cela, on définit les efforts de cohésion, ou efforts intérieurs, en chaque point de la courbe moyenne, sous la forme d'un torseur d'action appelé « torseur de cohésion » ou « torseur des efforts intérieurs ». Si l'on effectue une coupure selon une section droite (principe de la coupe), les efforts de cohésion sont les efforts qu'exerce un des tronçons sur l'autre. On a donc deux conventions :
- la convention des efforts à gauche : on considère les efforts qu'exerce le tronçon de gauche sur le tronçon de droite (à droite sur la figure ci-contre) ;
- la convention des efforts à droite : on considère les efforts qu'exerce le tronçon de droite sur le tronçon de gauche (à gauche sur la figure ci-contre).

Si l'on choisit le repère de sorte que x soit tangent à la courbe moyenne au niveau de la coupure, alors le torseur de cohésion s'obtient en écrivant le principe fondamental de la statique sur le tronçon considéré, et s'écrit de manière générale :
- ou bien
- N, effort normal : force de direction tangente à la courbe moyenne ;
- T ou V, effort tranchant : force perpendiculaire à la courbe moyenne et provoquant un cisaillement :
- Ty ou Vy : effort tranchant selon y,
- Tz ou Vz : effort tranchant selon z ;
- Mf, moment fléchissant : moment dont le vecteur est perpendiculaire à la courbe moyenne et provoquant une flexion :
- Mfy : moment fléchissant selon y,
- Mfz : moment fléchissant selon z ;
- Mt, moment de torsion : son vecteur a pour direction x.
En deux dimensions, la simplification consiste à considérer que seul un effort tranchant, un effort de traction et un moment fléchissant est transmis de section à section, suivant le principe de la coupe. En général, on se place dans le plan (Gxy), le torseur de cohésion devient donc.
On peut représenter de manière simple la sollicitation de la poutre en traçant le diagramme des efforts transmis de section à section en fonction de la position le long de la poutre, c'est-à-dire que l'on représente N(x), Ty(x), Tz(x), Mt(x), Mfy(x) et/ou Mfz(x). Ce diagramme est parfois appelé à tort diagramme des contraintes.
On représente ces derniers comme des fonctions le long de l'axe des en traçant des lignes.
Contraintes[modifier | modifier le code]
Les efforts de cohésion sont des grandeurs macroscopiques, définies sur l'ensemble de la section. Du fait de la linéarité du problème (on reste en petites déformations), on peut considérer indépendamment chaque composante, c'est-à-dire considérer que la poutre n'est soumise à chaque fois qu'à une seule sollicitation simple.
Le principe d'équivalence établit une relation entre chaque effort de cohésion et les contraintes générées localement en chaque point de la section. Pour les sollicitations complexes, on somme les contraintes de toutes les sollicitations simples (principe de superposition).
Selon le principe de Saint-Venant, les efforts sont correctement représentés lorsqu'on s'éloigne du point d'application. Ainsi, si localement cette modélisation ne donne pas de bons résultats, on peut les considérer comme presque corrects dès que la distance au point d'application dépasse plusieurs fois le diamètre de la section. Ce principe n'est valable que pour des poutres massives, pour la plupart des autres cas il est faux. Il faut en ce sens entendre « poutre massive » lorsqu'ici est évoqué la notion de poutre.
Par la suite, la grandeur S désigne l'aire de la section droite.
Traction simple[modifier | modifier le code]

L'effort normal N correspond à de la traction simple, on a donc la contrainte uniforme
- .
Cisaillement[modifier | modifier le code]


Les efforts tranchants Ty et Tz causent le cisaillement, mais il faut distinguer deux cas : celui du cisaillement simple et celui de la flexion simple. Dans les deux cas, les efforts extérieurs sont appliqués parallèlement à la section droite, c'est-à-dire perpendiculairement à la courbe moyenne.
Dans le cas du cisaillement simple, les efforts sont appliqués à la même abscisse x. Hormis au droit des points d'application des efforts, les contraintes sont uniformes (principe de Barré de Saint-Venant) :
- , et
- .

Si l'on isole un petit élément cubique de matière, on voit que la cission qu'il subit sur les sections droites devraient le faire tourner. Il subit donc également une cission sur les faces perpendiculaires à l'axe (Gy)[3]. Il y a donc également cisaillement entre les fibres adjacentes. On peut voir cela en faisant fléchir un paquet de cartes : les cartes glissent les unes sur les autres ; la poutre peut se voir comme un paquet dont les cartes seraient collées, la force de l'adhérence empêchant les cartes de glisser.


Dans le cas de la flexion simple, les efforts sont appliqués à des abscisses différentes. Cette contrainte ne génère que peu de risque de rupture et est donc généralement négligée (modèle de Bernoulli). Dans ce cas-là, la répartition des contraintes n'est plus uniforme (principe de Saint-Venant n'est plus valide) : la contrainte sur une surface libre est nécessairement dans le plan de la surface, donc la cission sur les faces extérieures est nulle. On a donc une cission qui croît lorsque l'on s'approche de la fibre neutre. La contrainte maximale vaut alors :
- poutre de section rectangulaire pleine : ;
- poutre de section circulaire pleine : ;
- tube circulaire mince : ;
où S est l'aire de la section droite. On voit que sur ces exemples là, la contrainte est 1,5 à 2 fois supérieure au cas du cisaillement simple.
Flexion pure[modifier | modifier le code]

Les moments fléchissants Mfy et Mfz correspondent à de la flexion. Du fait de l'hypothèse de Bernoulli (les sections droites restent perpendiculaires à la courbe moyenne) :
- la fibre neutre a un allongement nul ;
- les fibres à l'extérieur de la courbure sont étirées ;
- les fibres à l'intérieur de la courbure sont comprimées.
La contrainte varie de manière linéaire :
où IGz est le moment quadratique d'axe (Gz), calculé en fonction de la forme de la section droite.
Le risque de rupture se situe sur la face en extension de la poutre. Si l'on appelle V l'ordonnée du point situé sur cette face, la contrainte y vaut :
- .
La grandeur IGz/V est appelée « module de flexion ».
Si la poutre est symétrique et de hauteur h, on a
- V = ±h/2.
- Note
- Comme c'est la valeur absolue de la contrainte qui nous intéresse, on trouve souvent les expressions
- et
- .
Torsion[modifier | modifier le code]
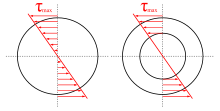
Nous nous plaçons dans le cas d'une poutre cylindrique (typiquement un arbre de transmission) et en petites déformations. La torsion provoque une contrainte de cisaillement τ qui est proportionnelle à la distance r par rapport à l'axe :
où :
- Mt est le moment de torsion ;
- IG est le moment quadratique de torsion, dépendant de la forme de la section (diamètre extérieur, et diamètre intérieur dans le cas d'un tube).
Si Mt est exprimé en N mm, que IG est en mm4 et r est en mm, alors τ(r ) est en MPa. La contrainte de cisaillement maximale vaut
où v est le rayon extérieur de la pièce. La quantité (IG/v ) est appelée module de torsion, et est exprimé en mm3 pour les calculs.
Le moment quadratique et le module de torsion sont en général tabulés en cm4 et cm3 respectivement.
Sollicitations composées[modifier | modifier le code]



En décomposant la sollicitation composée en sollicitations simples, on peut déterminer le tenseur des contraintes en tout point. Il faut ensuite déterminer un effort de comparaison suivant un des critères de Tresca ou de von Mises.
On distingue trois cas habituels :
- traction ou compression + flexion : cas d'un effort parallèle à l'axe, mais s'exerçant à distance de l'axe, ou bien cas d'un réservoir d'eau sous pression ;
- flexion déviée : effort ne se faisant pas selon un axe ;
- flexion + torsion : cas d'un arbre transmettant une puissance via un pignon ou une poulie : la force est perpendiculaire à l'axe et à distance de l'axe.
Dans ce dernier cas, on peut se ramener à un cas de flexion simple en calculant un moment de torsion idéal et un moment de flexion idéal (formule de Coulomb, formule de Rankine, formule de Saint Venant).
Déformée[modifier | modifier le code]
Dans le cas d'une poutre, on s'intéresse exclusivement à la forme finale de la fibre neutre. L'équation u (x ) de cette courbe est appelée « déformée ». Dans ce qui suit, nous considérons que la fibre neutre initiale est un segment de droite de longueur l0.
En traction-compression[modifier | modifier le code]
La fibre neutre reste droite, et la longueur finale l est donnée par l'intégration de la loi de Hooke :
- ,
- avec l'effort normal.
En flexion d'axe z[modifier | modifier le code]
Intuitivement, la courbure γ en un point est proportionnelle au moment fléchissant Mf, et inversement proportionnelle à la rigidité de la poutre. Cette rigidité dépend du matériau, par le module de Young E, et du profil de la section droite, par le moment quadratique IGz. On a donc :
- .
Par ailleurs, en petites déformations, on peut faire l'hypothèse que
soit
- .
Cette équation différentielle est souvent notée
- .
Si la poutre est de section constante et de matériau homogène, alors le terme EIGz est une constante et l'on obtient la déformée en intégrant simplement deux fois Mf par rapport à x, en tenant compte des conditions aux limites.


Par exemple, dans le cas d'une poutre de longueur L sur deux appuis avec une force F s'exerçant en son centre :
- sur la première moitié (0 ≤ x ≤ L/2), le moment fléchissant vaut , donc
- .
- Par symétrie, la poutre est horizontale en son centre (condition limite), on a soit
- et ainsi
- .
- Donc
- .
- Le déplacement est nul aux appuis (condition limite) donc soit B = 0. On a donc
- .
- La forme de la deuxième moitié est symétrique ; elle est décrite par un autre polynôme de forme similaire.
- La flèche (déplacement maximal) est au centre x = L/2 :
- .
En torsion[modifier | modifier le code]
Nous ne considérons ici que le cas d'une poutre cylindrique de longueur L. Une extrémité tourne par rapport à l'autre d'un angle θ (en radians). On peut donc définir un angle de torsion unitaire α = θ/L (en rad/m).
De manière intuitive, cet angle unitaire dépend :
- de l'effort, c'est-à-dire du moment de torsion Mt supposé ici uniforme ;
- de la rigidité de la poutre, qui dépend :
- de la rigidité du matériau, via le module de Coulomb G,
- de la rigidité de la section, via son moment quadratique de torsion IG ;
soit
- .
Donc, si l'on suppose que la section en x = 0 reste fixe, la section à l'abscisse x quelconque a tourné de
et en particulier
- .
Flexion hyperstatique[modifier | modifier le code]
Un cas fréquemment étudié est celui d'une poutre hyperstatique en flexion. Dans ce cas-là, les équations de la statique ne suffisent pas à déterminer les efforts aux appuis. On utilise deux méthodes de résolution :
- la méthode de superposition : on décompose le chargement en deux cas isostatiques ;
- la méthode de l'intégration : on résout l'équation différentielle linéaire d'ordre deux EIGzy '' = Mf, en appliquant les conditions aux limites adaptées.
Notes et références[modifier | modifier le code]
- (en) Roberto Ballarini, The Da Vinci-Euler-Bernoulli Beam Theory?, in Mechanical Engineering Magazine Online, (lire en ligne)
- (en) Seon M. Han, Haym Benaroya et Timothy Wei, Dynamics of Transversely Vibrating Beams using four Engineering Theories, in Mechanical Engineering Magazine Online, (lire en ligne)
- C'est une condition d'équilibre pour empêcher la rotation de l'élément cubique, la conséquence est que le tenseur des contraintes est une matrice symétrique.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Jean-Louis Fanchon, Guide de mécanique, Nathan, , 543 p. (ISBN 2-09-178965-8), p. 265-396
- Claude Hazard, Frédy Lelong et Bruno Quinzain, Mémotech — Structures métalliques, Paris, Casteilla, , 352 p. (ISBN 2-7135-1751-6), p. 326-336
- D. Spenlé et R. Gourhant, Guide du calcul en mécanique : maîtriser la performance des systèmes industriels, Paris, Hachette, , 272 p. (ISBN 2-01-168835-3), p. 130-208
Articles connexes[modifier | modifier le code]
- Mécanique des milieux continus
- Résistance des matériaux
- Stephen Timoshenko
- Théorie des coques
- Théorie des plaques
- Rotule plastique
- Jacques Bernoulli
Liens externes[modifier | modifier le code]
- Cours des Mines de Paris (licence Creative Commons)
- Formule de calcul des poutres simples en deux dimensions
- Approche mathématique des poutres
- Cours sur la méthode des éléments finis d'Yves Debard de l'université du Mans [PDF] :
- Calcul statique linéaire pour poutres, Guide de validation des progiciels de calcul de structure, ICAB
- Calcul de poutre et instabilités au flambement, déversement, voilement, manuel de référence du logiciel ICAB Force
- Mécanique des structures & étude des poutres de Patrice Cartraud, École Centrale de Nantes






































