Hyperbole (mathématiques)

Hyperbole obtenue comme intersection d'un cône et d'un plan parallèle à l'axe du cône.
Si l'on incline légèrement le plan, l'intersection sera encore une hyperbole tant que l'angle d'inclinaison reste inférieur à l'angle que fait une génératrice avec l'axe du cône.

En mathématiques, une hyperbole est une courbe plane obtenue comme la double intersection d'un double cône de révolution avec un plan. Elle peut également être définie comme une conique d'excentricité supérieure à 1, ou comme l'ensemble des points dont la différence des distances à deux points fixes est constante.

Le nom d'« hyperbole » (application par excès) lui est donné par Apollonios de Perga, remarquant, dans sa construction, que l'aire du carré construit sur l'ordonnée excède l'aire d'un rectangle de hauteur fixe construit sur l'abscisse (voir section Histoire).

Une hyperbole est constituée de deux branches disjointes symétriques l'une de l'autre et possédant deux asymptotes communes.

On peut rencontrer l'hyperbole dans de nombreuses circonstances comme lors de la représentation graphique de la fonction inverse, $x\to 1/x$ et de celle de toutes les fonctions qui lui sont associées : $x\to ax+b+{\frac {c}{x+d}}$, ou encore dans l'ombre créée par le pourtour ou un abat jour circulaire d'une source de lumière sur un mur, dans la trajectoire de certains corps dans l'espace ou dans les interférences produites par deux sources d'ondulations de même fréquence. C'est également la courbe suivie, pendant une journée, par l'extrémité de l'ombre du gnomon d'un cadran solaire de style polaire.

L'hyperbole intervient dans d'autres objets mathématiques comme les hyperboloïdes, le paraboloïde hyperbolique, les fonctions hyperboliques (sinh, cosh, tanh). Sa quadrature, c'est-à-dire le calcul de l'aire comprise entre une portion d'hyperbole et son axe principal, est à l'origine de la création de la fonction logarithme.

Arc d'hyperbole dessinée par l'ombre créée par une lampe.

Définitions géométriques

Intersection d'un cône et d'un plan

On considère un cône de révolution engendré par la rotation d'une droite (OA) autour d'un axe (Ox) et on appelle θ l'angle géométrique entre ces deux droites. On prend d'autre part un plan dont la normale fait avec l'axe (Ox) un angle supérieur à π/2 - θ. Si le plan ne passe pas par O, il coupe le cône suivant une hyperbole. Si le plan passe par O, il coupe le cône selon deux droites sécantes en O.

Lorsqu'une lampe munie d'un abat-jour est placée non loin d'un mur vertical, la courbe qui délimite, sur le mur, la zone éclairée et la zone ombragée est un arc d'hyperbole. En effet, la lumière est diffusée selon un cône — les rayons lumineux partent du centre de l'ampoule et s'appuient sur le cercle de l'ouverture de la lampe — coupé par un plan parallèle à l'axe du cône — le mur.

Principe des lignes de déclinaison d'un cadran solaire.

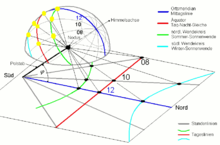
C'est également ce principe qui explique l'existence d'hyperboles sur certains cadrans solaires. Au cours d'une journée, les rayons du soleil passant par la pointe du gnomon dessinent une portion de cône dont l'axe, parallèle à l'axe de rotation de la terre, passe par la pointe du gnomon. L'ombre de cette pointe, sur le plan du cadran solaire dessine alors une portion d'hyperbole, appelé arc diurne ou ligne de déclinaison, intersection du cône et d'un plan. Au cours de l'année, l'angle du cône varie. Aux équinoxes, il est de 90°, le cône est un plan et l'ombre dessine une droite. Aux solstices, l'angle est de 66° 34' et l'ombre dessine une hyperbole.

La construction de l'hyperbole comme section d'un cône et d'un plan peut être réalisée à l'aide d'un compas parfait.

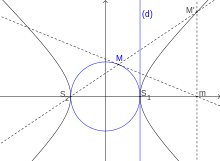
Définition par foyer et directrice

Hyperbole d'excentricité 3/2, avec son foyer F, sa directrice (D), ses asymptotes et son cercle principal.
La distance MF est toujours égale à une fois et demi la distance MH.

Soient (D) une droite et F un point n'appartenant pas à (D), et soit P le plan contenant la droite (D) et le point F. On appelle hyperbole de droite directrice (D) et de foyer F l'ensemble des points M du plan P vérifiant

$\qquad {\frac {\mathrm {d} (\mathrm {M} ,\mathrm {F} )}{\mathrm {d} (\mathrm {M} ,(\mathrm {D} ))}}=e\qquad e>1$

où d(M, F) mesure la distance du point M au point F et d(M, (D)) mesure la distance du point M à la droite (D).

La constante e est appelée excentricité de l'hyperbole. Elle est caractéristique de la forme de l'hyperbole : si l'on transforme l'hyperbole par une similitude, son excentricité reste inchangée. Elle est donc indépendante du choix arbitraire de repère orthonormé pour ce plan ; elle détermine tous les autres rapports de distances (et toutes les différences angulaires) mesurés sur l'hyperbole. Plus e est grand, plus l'hyperbole s'évase, les deux branches se rapprochant de la directrice. Plus e s'approche de 1 plus l'hyperbole s'arrondit, les deux branches s'éloignant l'une de l'autre, celle située dans le même demi-plan que le foyer se rapprochant d'une parabole.

Notons K le projeté orthogonal de F sur (D). (KF) est alors clairement un axe de symétrie de l'hyperbole appelé axe focal.

L'axe focal coupe l'hyperbole en deux points appelés les sommets S et S' de l'hyperbole.

La médiatrice du segment [SS'] est également un axe de symétrie de l'hyperbole appelé axe non focal. Le point d'intersection des deux axes, noté O, est alors le centre de symétrie de l'hyperbole.

Le cercle de diamètre [SS'] est appelé cercle principal de l'hyperbole.

Trace du cône (Γ), du plan (P) , de la sphère (Σ) et du plan (P') dans le plan passant par l'axe du cône et perpendiculaire à (P). La section du plan et du cône est une hyperbole de foyer F de directrice passant par K, de sommet S et d'excentricité SF/SK.

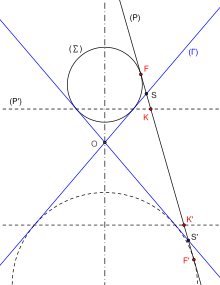
La symétrie orthogonale par rapport à l'axe non focal envoie le foyer F et la directrice (D) en F' et (D'). Par symétrie, l'hyperbole est également l'hyperbole de foyer F', de directrice (D') et d'excentricité e.

Une telle hyperbole possède en outre deux asymptotes passant par O et par les points d'intersection du cercle principal et des directrices. Ces points sont également les projetés orthogonaux des foyers sur les asymptotes. Lorsque les deux asymptotes sont perpendiculaires, on dit que l'hyperbole est équilatère.

En relation avec la définition précédente, l'hyperbole obtenue comme section de cône et de plan peut être définie par foyer et directrice. On considère une sphère (Σ) inscrite dans le cône (Γ) et touchant le plan (P) en F (sphère de Dandelin) et (P') le plan contenant le cercle de tangence de la sphère et du cône. L'hyperbole est de foyer F et de directrice (D) droite d'intersection des deux plans (P) et (P'). Dans le plan perpendiculaire à (P) et passant par l'axe du cône, se trouvent le point F, le sommet S et le point K. L'excentricité est donnée par le rapport SF/SK. Elle ne dépend que de l'inclinaison du plan par rapport à l'axe du cône. Si l'on appelle (d) la trace de (P) dans le plan perpendiculaire à (P) passant par l'axe du cône, si l'on note α l'angle entre (d) et l'axe du cône et θ l'angle du cône, l'excentricité est de cos(α)/cos(θ).

Propriété de divergence d'une lentille hyperbolique.

Cette relation entre foyer, directrice et excentricité dans une hyperbole est exploitée dans la construction des lentilles divergentes : si l'indice de la lentille par rapport au milieu est de e, et si la surface concave de la lentille est une hyperbole de foyer F et d'excentricité e, le faisceau de rayons parallèles traversant la lentille, se disperse comme si les rayons venaient du foyer F.

---

Définition bifocale

La tangente en $M$ est aussi une bissectrice.

L'hyperbole est le lieu géométrique des points dont la différence des distances aux deux foyers est constante.

Géométriquement, cela donne :

Soient F et F' deux points distincts du plan, distants de 2c et soit a un réel strictement compris entre 0 et c. On appelle hyperbole de foyers F et F' l'ensemble des points M du plan vérifiant la propriété suivante :

$\qquad \mid \mathrm {d} (\mathrm {M} ,\mathrm {F} )-\mathrm {d} (\mathrm {M} ,\mathrm {F} ')\mid =2a.$

L'axe focal est le nom de la droite portant les deux foyers : c'est l'un des deux axes de symétrie de l'hyperbole, le seul qui la coupe. Pour cette raison, on le nomme aussi axe transverse et ses points communs avec la courbe sont les sommets S et S' de l'hyperbole. Le réel a de la définition ci-dessus apparaît comme la moitié de la distance entre les sommets. Les directrices de l'hyperbole passent par les points de contact des tangentes au cercle principal (cercle de diamètre [SS']) issues des foyers.

En chaque point M de cette hyperbole, la bissectrice du secteur angulaire (FMF') se trouve être la tangente en M à la courbe.

Cette construction de l'hyperbole permet d'expliquer la présence d'hyperbole lors d'interférences entre deux sources de même fréquence. Au point M le déphasage de l'onde par rapport à la source S₁ est proportionnel à la distance MS₁. Le déphasage entre l'onde venant de S₁ et l'onde venant de S₂ est donc proportionnel à la différence des distances. Les deux ondes s'annulent quand leur déphasage est égale à (2k+1)π. Les deux ondes s'amplifient quand leur déphasage est de 2kπ. Les points où l'onde résultante a une amplitude nulle et les points où l'onde résultante a une amplitude maximale dessinent donc un faisceau d'hyperboles de foyers S₁ et S₂.

Il existe des mécanismes avec corde et poulie exploitant cette propriété des hyperboles pour effectuer leur tracé. c'est le cas du dispositif conçu par Ibn Sahl au X^e siècle.

Construction mécanique d'une hyperbole selon la méthode d'Ibn Sahl. La règle pivote autour du foyer F2. Le crayon M, sur la règle s'appuie sur une corde F1MD de longueur fixe et dessine une portion d'hyperbole de foyers F1 et F2.

Interférences produites par deux sources synchrones avec les lignes nodales et anti-nodales.

Image d'un cercle par une homographie

Comme toute conique, l'hyperbole peut être considérée comme l'image d'un cercle par une transformation projective. Plus précisément, si (H) est une hyperbole et (C) un cercle, il existe une transformation projective qui transforme (C) en (H). Par exemple, l'hyperbole est l'image de son cercle principal par une transformation projective dont l'expression analytique, dans un repère orthonormé porté par ses axes de symétrie, est

${\begin{cases}x'={\frac {a^{2}}{x}}\\y'={\frac {by}{x}}.\end{cases}}$

où a est le rayon du cercle principal et ± b/a les pentes de ses asymptotes.

Cette propriété permet de transférer à l'hyperbole des propriétés touchant des règles d'incidence de droites dans un cercle, comme le théorème de Pascal.

Parmi les transformations projectives, il en est de particulières comme les homologies harmoniques. Ce sont des homologies involutives de centre I d'axe (d) et de rapport -1. Dans celles-ci, un point M, son image M', le centre I et le point m d'intersection de (IM) avec (d) sont en division harmonique.

Un cercle (C) a pour image une hyperbole par une homologie harmonique de centre I et d'axe (d) si et seulement si l'image (d') de l'axe (d) par l'homothétie de centre I et de rapport 1/2 coupe le cercle en deux points. Réciproquement, une hyperbole étant donnée, il est possible de trouver des cercles et des homologies harmoniques associées échangeant hyperbole et cercle. Exemple :

• une hyperbole de foyer F, de directrice (d) et d'excentricité e est l'image du cercle de centre F et de rayon eh (où h est la distance entre le foyer et la directrice) par l'homologie harmonique de centre F et d'axe (d₁) image de (d) dans l'homothétie de centre F et de rapport 2 ;
• une hyperbole équilatère est l'image de son cercle principal par une homologie harmonique de centre un des sommets et d'axe (d) passant par l'autre sommet et perpendiculaire à l'axe principal de l'hyperbole. Quand l'hyperbole n'est pas équilatère, elle reste l'image d'un cercle par une homologie harmonique de centre un des sommets, mais le cercle n'est plus le cercle principal et l'axe ne passe plus par l'autre sommet. Ce sont des homologies de ce type qui permettent de démontrer le théorème de Frégier.

L'hyperbole et le cercle sont homologues dans l'homologie harmonique de centre F et d'axe (d1).

L'hyperbole équilatère et son cercle principal sont homologues dans l'homologie harmonique de centre S2 et d'axe (d). Pour construire le point M', on mène par m une tangente au cercle qui touche le cercle en M. La droite (S2M) rencontre la perpendiculaire à l'axe focal passant par m en M'.

Relations entre les grandeurs caractéristiques d'une hyperbole

Les différentes grandeurs d'une hyperbole.

Les grandeurs (géométriques ou numériques) d’une hyperbole sont :

• la distance entre le centre de l'hyperbole et un de ses sommets généralement notée a ;
• la pente (en valeur absolue) que font les asymptotes avec l'axe focal, généralement notée b/a ;
• la distance séparant le centre de l'hyperbole et un des foyers, généralement notée c ;
• la distance séparant un foyer F de sa directrice (d) associée, généralement notée h ;
• la distance séparant le centre de l’hyperbole et une de ses deux directrices, généralement notée f ;
• l'excentricité de l’hyperbole (strictement supérieure à 1), généralement notée e ;
• le « paramètre » de l’hyperbole, généralement noté p, représentant le demi latus rectum (corde parallèle à la directrice et passant par le foyer).

Des relations existent entre ces grandeurs :

• si l’hyperbole est définie par son excentricité $e$ et la distance $h$ entre le foyer F et la directrice (d), alors :

  $a={eh \over e^{2}-1},\,b={eh \over {\sqrt {e^{2}-1}}},\,c={e^{2}h \over e^{2}-1},\,f={h \over e^{2}-1},\,p=eh\,;$

• si l’hyperbole est donnée par la distance entre le centre et un sommet $a$ et la pente des asymptotes $b/a$ alors :

  $c={\sqrt {a^{2}+b^{2}}},\,h={b^{2} \over {\sqrt {a^{2}+b^{2}}}},\,f={a^{2} \over {\sqrt {a^{2}+b^{2}}}},\,e={{\sqrt {a^{2}+b^{2}}} \over a},\,p={b^{2} \over a}\,;$

• lorsque l’on connait la distance entre le centre et le sommet $a$ et l’excentricité $e$ :

  $b=a{\sqrt {e^{2}-1}},\,c=ae,\,h={a(e^{2}-1) \over e},\,f={a \over e},\,p=a(e^{2}-1)\,.$

• enfin, dans la définition bifocale de l'hyperbole où sont connues la longueur 2a et la distance 2c entre les foyers :

  $b={\sqrt {c^{2}-a^{2}}},\,e={\frac {c}{a}},\,h={c^{2}-a^{2} \over c},\,f={a^{2} \over c},\,p={c^{2}-a^{2} \over a}\,.$

Équations

Équation dans un repère normé porté par les asymptotes

Cas particulier de la fonction inverse

Représentation graphique de la fonction inverse. Hyperbole avec ses foyers et ses directrices.

L'hyperbole dont l'expression mathématique est la plus simple est la représentation graphique de la fonction $f$ définie par $f(x)=1/x$, voir fonction inverse.

Cette hyperbole est équilatère parce que ses deux asymptotes sont orthogonales. Son excentricité vaut ${\sqrt {2}}$.

Démonstration

Montrons que le graphe de la fonction définie par $f(x)={\frac {1}{x}}$ est bien une hyperbole. On pose $u={\frac {1}{\sqrt {2}}}(y+x)\,,\,v={\frac {1}{\sqrt {2}}}(y-x)$ donc $x={\frac {1}{\sqrt {2}}}(u-v)\,,\,y={\frac {1}{\sqrt {2}}}(u+v).$ Ainsi à partir de $xy=1$ qui est l'équation de la courbe de la fonction inverse on obtient $u^{2}-v^{2}=2$

On prend alors l'équation générale d'une conique dans un repère orthonormé dont l'axe principal passe par le foyer et est perpendiculaire à la directrice : $(u-c)^{2}+v^{2}=e^{2}(u-f)^{2}$ où f est la distance du centre du repère à la directrice et c la distance du centre du repère au foyer.

En développant il vient :

$(e^{2}-1)u^{2}-v^{2}=(c^{2}-e^{2}f^{2})+2u(e^{2}f-c)$

ainsi avec $e={\sqrt {2}},\,c=2f,\,f=1$ on retrouve bien l'équation recherchée.

Cas général

Dans le repère $(O,{\vec {u}},{\vec {v}})$, où O est le centre de l'hyperbole et ${\vec {u}}$ et ${\vec {v}}$ les vecteurs unitaires directeurs des asymptotes, l'hyperbole a pour équation : $xy={\frac {c^{2}}{4}}$.

Réciproquement, si deux droites de vecteurs directeurs ${\vec {u}}$ et ${\vec {v}}$ se coupent en O et si une courbe, dans le repère $(O,{\vec {u}},{\vec {v}})$, a pour équation xy= Cste où Cste est un réel non nul, alors cette courbe est une hyperbole.

Équations dans des repères où l'axe focal est l'axe principal

Si le centre du repère est le centre de l'hyperbole

Dans un repère dont les axes sont de symétrie pour l'hyperbole, l'axe transverse pour axe des abscisses, l'équation cartésienne se met sous la forme ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$ donnant alors les représentations paramétriques $t\mapsto \left(a\,\cosh(t),b\,\sinh(t)\right)$ et $t\mapsto \left(-a\,\cosh(t),b\,\sinh(t)\right)$ pour chacune des branches.

Un autre paramétrage possible est : $y=b\tan t\quad x={\frac {a}{\cos t}}$

Son équation polaire est : $\rho ={\frac {b}{\sqrt {e^{2}\cos ^{2}(\theta )-1}}}$

Si le centre du repère est le foyer de l'hyperbole

Dans un repère orthonormé $(F,{\vec {i}},{\vec {j}})$ dans lequel ${\vec {i}}={\frac {1}{FK}}{\overrightarrow {FK}}={\frac {1}{h}}{\overrightarrow {FK}}$, l'hyperbole a pour équation cartésienne : $x^{2}+y^{2}=e^{2}(x-h)^{2}$

Son équation polaire, dans ce même repère est : $\rho ={\frac {p}{1+e\cos(\theta )}}$

où p = eh est le paramètre de l'hyperbole.

Si le centre du repère est le sommet de l'hyperbole

Dans un repère orthonormé $(S,{\vec {i}},{\vec {j}})$, l'hyperbole a pour équation cartésienne : $y^{2}=2px+(e^{2}-1)x^{2}$,

Équation générale de conique

De manière générale, comme toute conique, une hyperbole a une équation cartésienne de la forme $f(x,y)=0$ avec $f(x,y)=\alpha x^{2}+2\beta xy+\gamma y^{2}+2\delta x+2\epsilon y+\phi .$ Pour qu'une telle équation soit celle d'une hyperbole, il est nécessaire que $\alpha \gamma -\beta ^{2}<0.$ Dans ce cas, la conique a pour centre le point C dont les coordonnées (x₀, y₀) vérifient le système : ${\begin{cases}\alpha x+\beta y+\delta =0\\\beta x+\gamma y+\epsilon =0.\end{cases}}$ On reconnait les dérivées partielles : ${\begin{cases}{\frac {\partial f}{\partial x}}=0\\{\frac {\partial f}{\partial y}}=0\end{cases}}$

Un changement de repère, en prenant pour centre le point C, conduit à l'équation suivante : $\alpha X^{2}+2\beta XY+\gamma Y^{2}+f(x_{0},y_{0})=0$ qui sera l'équation d'une hyperbole si et seulement si f(x₀, y₀) est non nul.

Les directions des asymptotes sont les solutions de l'équation homogène $\alpha X^{2}+2\beta XY+\gamma Y^{2}=0$

Les asymptotes font un angle φ tel que: $\cos ^{2}\varphi ={\frac {(\alpha +\gamma )^{2}}{(\alpha -\gamma )^{2}+4\beta ^{2}}}$

L'hyperbole est équilatère si et seulement si α = - γ.

Si γ est non nul, les pentes des asymptotes sont les racines de l'équation aux pentes : $\gamma m^{2}+2\beta m+\alpha =0$, et si γ est nul, les directions ont pour équations : X = 0 et αX + 2βY=0.

Connaissant ses asymptotes (d1) : ax + by + c = 0 et (d2) : a'x + b'y + c' = 0, et un point M(u,v) de l'hyperbole , son équation est^{[réf. souhaitée]} :

$(ax+by+c)(a'x+b'y+c')=k$ avec $k=(au+bv+c)(a'u+b'v+c')$

Ce résultat provient du fait que les directions des asymptotes déterminent à une constante multiplicative près l'équation homogène, que leur point d'intersection détermine le centre de l'hyperbole et que la constante est fixée par le fait que la courbe passe par M.

Équation matricielle

L'équation précédente peut s'écrire sous forme matricielle :

$^{\mathrm {t} }\mathbf {x} \mathbf {A} \mathbf {x} +^{\mathrm {t} }\mathbf {b} \mathbf {x} +f=0$

où

• $\mathbf {x} ={\begin{pmatrix}x\\y\end{pmatrix}}$ ; ^tx est la transposée de x ;
• A est une matrice 2×2, $\mathbf {A} ={\begin{pmatrix}\alpha &\beta \\\beta &\gamma \end{pmatrix}}$ ;
• $\mathbf {b} ={\begin{pmatrix}2\delta \\2\epsilon \end{pmatrix}}$ ; ^tb est la transposée de b ;

avec toujours les mêmes contraintes.

Propriétés

Intérieur et extérieur

L'hyperbole partage le plan en 3 zones ou composantes connexes. Comme elle est la section d'un cône et d'un plan, on appelle intérieur de l'hyperbole les portions de plan situées à l'intérieur du cône, ce sont les zones qui contiennent les foyers, et extérieur de l'hyperbole la dernière zone, celle qui contient le centre de l'hyperbole.

Sécantes et sommets

Diamètres conjugués dans une hyperbole.

Soit M un point de l'hyperbole de sommets S et S' et de centre O. Si par un point N de l'hyperbole, on mène des parallèles à (SM) et (S'M), elles rencontrent l'hyperbole en deux points P et P' symétriques par rapport à O. Par conséquent, dans un faisceau de droites parallèles (d_i) rencontrant l'hyperbole, les milieux des cordes que déterminent ces droites sur l'hyperbole, sont alignés avec le centre O de l'hyperbole. De plus, si M est le point de l'hyperbole tel que (SM) soit parallèle à (d_i) alors la droite des milieux est parallèle à (S'M). Un telle droite passant par le centre de l'hyperbole est appelée diamètre de l'hyperbole.

Sécantes et asymptotes

Si une droite coupe l'hyperbole en M et M', alors elle coupe les asymptotes en P et P' et les segments [MM'] et [PP'] ont même milieu.

Soit (d) une droite non parallèle aux asymptotes. Si par un point M de l'hyperbole, on trace une parallèle à (d), elle rencontre les asymptotes en P et P' et le produit ${\overline {MP}}\times {\overline {MP'}}$ est indépendant du point M.

Hyperbole équilatère

Une hyperbole est dite équilatère lorsque ses deux asymptotes sont perpendiculaires.

Théorème de Brianchon-Poncelet — Lorsqu'un triangle est inscrit dans une hyperbole équilatère, son orthocentre est aussi sur l'hyperbole.

Ce deuxième résultat a été attribué à Karl Feuerbach par Julian Coolidge, mais il n'apparait dans aucun ouvrage avant ceux de Brianchon et Poncelet.

Théorème conique de Feuerbach — Le lieu des centres des hyperboles équilatères circonscrites à un triangle est le cercle d'Euler du triangle.

Tangentes

Si l'hyperbole a pour équation ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,$ la tangente au point M de coordonnées (x₀, y₀) a pour équation : ${\frac {x_{0}}{a^{2}}}x-{\frac {y_{0}}{b^{2}}}y=1$

Comme une tangente est une sécante particulière, la propriété des sécantes et des sommets offre un moyen de tracer une tangente en un point M distinct des sommets : la droite passant par un des sommets S de l'hyperbole et parallèle à (OM) rencontre l'hyperbole en N, la tangente est alors parallèle à (S'N).

Si M est un point de l'hyperbole distinct des sommets, la tangente en M est également la bissectrice intérieure de l'angle FMF' où F et F' sont les foyers de l'hyperbole et le produit des distances des foyers à la tangente est toujours égal à b². Cette propriété a quelques applications pratiques. Elle fournit un moyen simple de construire la tangente en un point comme bissectrice intérieure de (F'MF). Dans un miroir de forme hyperbolique, les rayons issus d'un foyer sont réfléchis comme s'il provenaient de l'autre foyer. Bergery préconise donc, pour éviter les déperditions de chaleur, de construire le fond d'un cheminée selon un cylindre hyperbolique.

La tangente en un point M coupe les asymptotes en deux points P et P' symétriques par rapport à M.

Construction des deux tangentes à l'hyperbole issues de M à l'aide du cercle directeur.

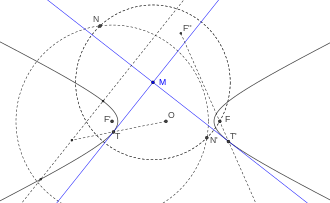
Par le point O ou un point M intérieur à l'hyperbole, il ne passe aucune tangente, par un point situé sur l'hyperbole ou sur une asymptote (distinct de O), il en passe une seule et par un point situé à l'extérieur de l'hyperbole, non situé sur les asymptotes, il passe toujours deux tangentes. Pour construire les deux tangentes issues de M, il suffit de tracer le cercle de centre M passant par un foyer F et le cercle de centre F' et de rayon 2a. Les cercles se rencontrent en N et N', les médiatrices de [FN] et [FN'] sont les tangentes recherchées. Pour trouver le point de contact, il suffit de construire une parallèle à la tangente coupant l'hyperbole en deux points, la droite passant par O et par le milieu de la corde ainsi construite rencontre la tangente en son point de contact. Ou bien, on prend le symétrique d'un des foyers par rapport à la tangente, la droite joignant ce symétrique à l'autre foyer rencontre la tangente à son point de contact.

Cercles

Cercle principal : c'est le cercle de diamètre [SS']. Foyer et directrice sont en relation pôle/polaire par rapport au cercle principal. Le cercle principal, privé de ses intersections avec les asymptotes, est également la podaire de l'hyperbole par rapport à l'un des foyers, c'est-à-dire le lieu des projetés orthogonaux de ce foyer sur les tangentes, ce qui fait de l'hyperbole, l'antipodaire de son cercle principal par rapport à un de ses foyers.

Cercle directeur : c'est un cercle passant par un foyer et de rayon égal à 2a. Selon la définition bifocale de l'hyperbole, l'hyperbole est le lieu des centres des cercles passant par F et tangents intérieurement ou extérieurement au cercle directeur de centre F'. L'ensemble des médiatrices des segments [FM], où M parcourt le cercle directeur de centre F' donne l'ensemble des tangentes à l'hyperbole, le cercle directeur est donc l'orthotomique de l'hyperbole par rapport à un foyer, c'est-à-dire l'ensemble des symétriques de F par rapport aux tangentes.

Cercle orthoptique : si l’excentricité est strictement comprise entre 1 et √2, il existe des points M par lesquelles passent deux tangentes orthogonales. L'ensemble de ces points M dessine un cercle de centre O et de rayon √a²-b², appelé cercle orthoptique de l'hyperbole.

Construction du centre de courbure au point M, du cercle osculateur et développée de l'hyperbole.

Cercles osculateurs : en tout point M de l'hyperbole, il existe un cercle possédant un point de contact triple avec l'hyperbole. C'est le cercle osculateur à l'hyperbole au point M. Son centre, appelé centre de courbure, est situé sur la normale à la courbe (qui est aussi la bissectrice extérieure de l'angle FMF') a une distance de M égale au rayon de courbure. Si l'hyperbole a pour équation : ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,$ le rayon du cercle osculateur au point d'abscisse x₀ a pour valeur : $r={\frac {\left(e^{2}x_{0}^{2}-a^{2}\right)^{3/2}}{ab}}.$ Il est possible de construire géométriquement le centre du cercle osculateur en M. Si (t) et (n) sont respectivement la tangente et la normale à l'hyperbole au point M, on trace le symétrique M' de M par rapport à l'axe principal et le symétrique (t') de (t) par rapport à (MM'), cette droite rencontre la droite (OM') en N. La perpendiculaire à (t') en N rencontre la normale (n) au centre de courbure.

La développée de l'hyperbole, c'est-à-dire le lieu des centres de courbure est une courbe de Lamé d'équation : $\left({\frac {ax}{c^{2}}}\right)^{2/3}-\left({\frac {by}{c^{2}}}\right)^{2/3}=1$

Longueur et aire

Si M(t₀) est un point de l'hyperbole d'équation paramétrée, $y=b\tan t\quad x={\frac {a}{\cos t}},$ où t₀ est compris entre 0 et π/2, la longueur de l'arc SM est $\int _{0}^{t_{0}}{\frac {\sqrt {b^{2}+a^{2}\sin ^{2}t}}{\cos ^{2}t}}\mathrm {d} t$ dont l'intégration nécessite l'utilisation des intégrales elliptiques.

L'aire d'une portion de plan délimitée par un arc d'hyperbole est à l'origine de la création de la fonction logarithme et des fonctions hyperboliques. L'aire de la surface délimitée par l'hyperbole d'équation yx = 1, l'axe des abscisses et les droites d'équation x = u et x = v est égale à |ln(v/u)|.

Histoire

Égalité d'aire, dans une hyperbole, entre le carré mené sur l'ordonnée et le rectangle bleu mené sur l'abscisse. Ce rectangle est plus grand que le rectangle de hauteur SP (paramètre de l'hyperbole) d'où le nom de hyperbole (ajustement par excès) donné à la courbe par Apollonios.

L'hyperbole est étudiée, dans le cadre des coniques, durant la période grecque. Ainsi Ménechme résout un problème de double proportionnelle en utilisant une hyperbole d'équation XY= constante. Mais pour Menechme et ses successeurs, Euclide et Aristée, cette courbe ne possède qu'une composante. Ils l'appellent «conique obtusangle» car ils la définissent comme l'intersection d'un cône obtusangle (cône engendré par la rotation d'un triangle ABC, rectangle en B, autour de AB et tel que l'angle de sommet A soit supérieur à 45 °) avec un plan perpendiculaire à sa génératrice. Apollonius de Perge semble être le premier à envisager les deux composantes de l'hyperbole. C'est également lui qui lui donne le nom d'«hyperbole» (ajustement par excès) ayant remarqué que l'aire du carré dessiné sur l'ordonnée est supérieure à celle du rectangle dessiné sur l'abscisse et dont la hauteur serait fixe.

Une demi-droite passant par l'origine intersecte l'hyperbole d'équation $x^{2}\ -\ y^{2}\ =\ 1$ au point $(\cosh \,a,\,\sinh \,a)$, où $a$ est le double de l'aire algébrique de la surface délimitée par la demi-droite, l'hyperbole et l'axe des $x$.

La recherche de l'aire sous l'hyperbole est entreprise, en 1647, par Grégoire de Saint-Vincent, qui met en évidence sa propriété logarithmique.

En 1757-1762, Vincenzo Riccati établit une relation entre l'aire d'un secteur angulaire dans une hyperbole et les coordonnées d'un point et définit les fonctions cosinus hyperbolique et sinus hyperbolique par analogie à la relation existant dans le cercle.

---

Bibliographie

• Patrice Tauvel, Géométrie : agrégation, licence 3e année, master, Paris, Dunod, 2005, 532 p. (ISBN 2-10-049413-9)
• Claude Lucien Bergery, Géométrie des courbes appliquée aux arts, Thiel, 1843 (lire en ligne)
• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-916352-08-4)
• Méthodes modernes en géométrie de Jean Fresnel
• Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)
• Bernard Vitrac, « Les géomètres de l'antiquité 8- Apollonius de Perge et la tradition des coniques », sur cultureMATH (Ressources pour les enseignants de mathématiques, site expert des Écoles normales supérieures et du Ministère de l'Éducation nationale

Annexes

Articles connexes

• Fonction hyperbolique
• Coniques
  • Ellipse
  • Parabole
• Conique dégénérée (en)

Liens externes

• http://www.mathcurve.com/courbes2d/hyperbole/hyperbole.shtml
• http://xavier.hubaut.info/coursmath/2de/belges.htm Coniques et théorème de Dandelin