Indice de réfraction

L'indice de réfraction (souvent noté n ; en anglais, index of refraction ou IOR) est une grandeur sans dimension caractéristique d'un milieu, décrivant le comportement de la lumière dans celui-ci ; il dépend de la longueur d'onde de mesure mais aussi des caractéristiques de l'environnement (notamment pression et température). L'indice de réfraction est parfois appelé « constante optique » d'un matériau, ce qui est un abus de langage, puisqu'il est à la fois variable selon des grandeurs qui lui sont extérieures, et non unique pour un milieu donné, car lié aux propriétés optiques, cristallographiques ou encore diélectriques de la matière, qui ne sont pas nécessairement isotropes.
L'indice absolu d'un milieu est son indice relatif par rapport au vide. Lorsqu'aucune indication n'est donnée quant au milieu de comparaison c'est de l'indice absolu dont il s'agit[1].
Bien qu'il soit communément supposé supérieur à 1, l'indice de réfraction peut en réalité prendre des valeurs bien différentes. Le vide a pour indice 1. Dans un milieu absorbant, l'indice de réfraction est un nombre complexe dont la partie imaginaire rend compte de l'atténuation de l'onde. Les milieux biréfringents possèdent deux indices, un ordinaire et un extraordinaire, voire trois indices. Certains matériaux particuliers peuvent avoir un indice dit non linéaire, tandis que des métamatériaux ont été élaborés avec des indices négatifs.
L'indice de réfraction intervient notamment dans les lois de Snell-Descartes, qui mettent en jeu le rapport des indices de réfraction. Cet effet, appelé réfraction, est à la base de la conception des lentilles optiques. L'angle de Brewster, le phénomène de réflexion totale ou encore les coefficients de Fresnel de transmission et de réflexion dépendent de l'indice de réfraction. Le fait que l'indice de réfraction dépende de la longueur d'onde est appelé dispersion et provoque la dispersion de la lumière dans les prismes ou dans les arcs-en-ciel.
Caractéristique d'une onde qui se propage, il est possible, en vertu de la dualité onde-corpuscule démontrée par la mécanique quantique, de mesurer l'indice de réfraction pour une onde de matière.
La mesure de l'indice de réfraction des matériaux, des gaz, et notamment de l'air, est un enjeu important pour de multiples applications. La précision nécessaire sur ces mesures dans le domaine de la physique et des matériaux demande l'utilisation d'instruments précis tels que les interféromètres. Le domaine de la mesure de l'indice de réfraction se nomme la réfractométrie.
Historique[modifier | modifier le code]
Une première approche de la loi de réfraction fut entreprise par Ptolémée au IIe siècle. Il donna des tables faisant correspondre angles d'incidence et angles de réfraction de la lumière pour les interfaces air/eau, air/verre et eau/verre. Ces valeurs semblaient obéir à une loi mais Ptolémée ne les traduisit pas par une formule mathématique et leur correspondance avec les valeurs réelles reste approximative[2],[A 1]. La question du rapport entre angle de réfraction et angle d'incidence fut aussi posée par Ibn Sahl au Xe siècle, faisant de lui un des précurseurs de l'élaboration de la loi de réfraction[3]. Sans peut-être avoir une claire conscience de son importance, il utilisa en effet comme caractéristique de l'opacité du milieu un rapport qui correspond au rapport des sinus des angles des rayons lumineux, c'est-à-dire à l'indice[4]. Ibn al-Haytham, à la même époque, lia la vitesse de la lumière à la densité de matière[5], mais ne donna pas de loi ni de table analysant la réfraction. Au contraire, Vitellion dans sa traduction et analyse de l'œuvre d'Ibn al-Haytham indiqua une table récapitulant angle de réfraction, d'incidence et de déviation pour les interfaces air-verre et air-eau. Pour Vitellion, les résultats indiquaient que la fonction est croissante, où i et r sont les angles d'incidence et de réfraction[A 1]. Malgré ces déductions, il est apparu que la reproduction des tables de réfraction était faussée, volontairement ou involontairement, en contradiction avec l'expérience, plus encore que les tables jadis écrites par Ptolémée[A 1].
Kepler, en 1604, analysant les résultats de Vitellion dans son « Des choses oubliées dans Witelo », trouva une loi de réfraction issue de raisonnements assez abscons : . Cette constante k était propre à un milieu donné et constituait pour Kepler une caractéristique des matériaux ; lorsqu'on la rapporte aux lois de réfraction découvertes plus tard, elle équivaut à et est sans doute une des premières approches réelles du concept d'indice de réfraction[A 1].
Il fallut attendre que la loi de la réfraction soit publiée pour que l'indice de réfraction apparaisse véritablement[6]. La loi en sinus de la réfraction aurait été découverte, quoique non publiée, au début des années 1600[réf. souhaitée] par Thomas Harriot[7]. La théorie d'Ibn Sahl fut redécouverte plus tard, de manière très confidentielle vers 1621, par le mathématicien hollandais Willebrord Snell Van Royen[8]. René Descartes publia cette loi de la réfraction dans « La Dioptrique » en 1637[7].

Descartes avait démontré la relation en se basant sur des hypothèses fausses sur la vitesse de la lumière. Il fallut attendre Christian Huygens en 1678 pour que la démonstration de la relation soit faite sur une base théorique saine[3],[N 1] ainsi que Isaac Newton en 1672 pour émettre l'hypothèse selon laquelle l'indice de réfraction est propre à chaque longueur d'onde, ce qui provoque la dispersion des couleurs d'un faisceau de lumière blanche passant par un prisme[9].
On doit aussi aux travaux de Huygens la découverte du phénomène dit de « double réfraction » de la calcite, qui met en évidence la biréfringence du cristal, faisant qu'un faisceau de lumière traversant le cristal est réfracté différemment selon sa polarisation[8]. En revanche, les travaux de Newton se basant principalement sur une hypothèse particulaire — la lumière composée de particules — n'expliquaient pas bien pourquoi la lumière se déplaçait différemment dans une matière ou l'autre.
Ce fut avec les travaux de Thomas Young et de Fraunhofer que fut clairement introduite la notion d'indice de réfraction. Augustin Fresnel théorisa par la suite le modèle ondulatoire pour la lumière et James Clerk Maxwell et Hermann von Helmholtz démontrèrent le fait que la lumière est une onde électromagnétique, permettant ainsi de décrire les milieux et relier l'indice de réfraction aux propriétés de ces milieux, notamment grâce à la permittivité diélectrique[7].
Origine physique de l'indice de réfraction[modifier | modifier le code]
L'indice de réfraction peut être défini comme « la manifestation macroscopique de la réponse microscopique de la matière à une force périodique »[N 2]. Plus précisément on peut dire que l'indice de réfraction résulte d'un phénomène microscopique de polarisation des atomes du fait de l'onde électromagnétique incidente.
La lumière est une onde électromagnétique oscillant périodiquement, elle est composée d'un champ magnétique et d'un champ électrique oscillants. Ces champs à leur arrivée à l'interface avec un matériau — dit milieu — vont interagir avec les champs et caractéristiques de ce milieu : forces d'interaction, liaisons chimiques, vitesse et vibrations des molécules. La principale action qu'exerce la lumière est celle du champ électrique sur les charges électriques du milieu, en les faisant osciller à la même fréquence que la lumière. Ceci produit un nouveau champ électromagnétique[10].
Ce nouveau champ électromagnétique possède la même fréquence mais pas la même phase que l'onde incidente : les deux ondes (lumière incident et milieu) s'additionnent et vont interférer, générant une nouvelle onde déphasée par rapport à l'onde d'origine.
La nouvelle onde se propage avec sa propre vitesse de propagation tandis que sa phase est proportionnelle au produit de cette vitesse de propagation et de l'épaisseur parcourue de matériau ; la vitesse de phase a changé et se différencie de la célérité de la lumière[10].
En fonction de la phase relative de l'onde motrice d’origine et des ondes rayonnées par le mouvement des charges, il existe plusieurs possibilités :
- Si les électrons émettent une onde lumineuse déphasée de 90° par rapport à l'onde lumineuse qui les excite, l’onde lumineuse totale se déplacera plus lentement. Il s'agit de la réfraction normale des matériaux transparents comme le verre ou l’eau, et correspond à un indice de réfraction réel supérieur à 1[11].
- Si les électrons émettent une onde lumineuse déphasée de 270° par rapport à l’onde lumineuse qui les excite, l’onde se déplacera plus rapidement. C’est ce qu’on appelle la « réfraction anormale », et elle est observée près des raies d’absorption (généralement dans le spectre infrarouge), avec les rayons X dans les matériaux ordinaires et avec les ondes radio dans l'ionosphère terrestre. Cela correspond à une permittivité inférieure à 1, ce qui fait que l'indice de réfraction est également inférieur à l’unité et que la vitesse de phase de la lumière est supérieure à la vitesse de la lumière dans le vide c (la vitesse du signal est cependant toujours inférieure à c, comme indiqué ci-dessus). Si la réponse est suffisamment forte et déphasée, le résultat est une valeur négative de permittivité et un indice de réfraction imaginaire, comme observé dans les métaux ou le plasma[11].
- Si les électrons émettent une onde lumineuse déphasée de 180° par rapport à l’onde lumineuse qui les excite, elle interférera de manière destructrice avec la lumière d’origine pour réduire l’intensité lumineuse totale. Il s’agit de l’absorption de la lumière dans les matériaux opaques et correspond à un indice de réfraction imaginaire.
- Si les électrons émettent une onde lumineuse qui est en phase avec l’onde lumineuse qui les excite, cela amplifiera l’onde lumineuse. Ceci est rare, mais se produit dans les lasers en raison de l'émission stimulée. Il correspond à un indice imaginaire de réfraction, de signe opposé à celui d'absorption.
Pour la plupart des matériaux en lumière visible, la phase se situe entre 90° et 180°, ce qui correspond à une combinaison de réfraction et d’absorption.
Expressions[modifier | modifier le code]
L'indice étant le résultat de phénomènes complexes d'interaction entre les champs et les atomes de la matière, plusieurs formules permettent d'exprimer .
Expression courante[modifier | modifier le code]
La définition la plus répandue pour l'indice de réfraction est qu'il est la quantité résultant du rapport entre la vitesse de la lumière dans le vide, et la vitesse de phase de la lumière dans ce milieu[12] :
Cette définition possède plusieurs défauts. D'une part, du fait que la vitesse de la lumière dans le vide est une limite supérieure à la vitesse de la lumière, on pourrait en déduire que l'indice de réfraction ne peut pas être inférieur à , ce qui est faux. La vitesse considérée ici est une vitesse de phase, qui elle n'est pas limitée par la vitesse de la lumière, elle caractérise en effet la phase de l'onde et non l'onde elle-même — qui, elle, est limitée par la vitesse de la lumière dans le vide. D'autre part, du fait qu'il est un rapport de vitesse, on pourrait croire que l'indice de réfraction ne peut prendre que des valeurs réelles, ce qui est aussi faux[13].
Expression générale[modifier | modifier le code]
Une autre définition de l'indice de réfraction le lie à une autre caractéristique du milieu, la permittivité diélectrique ε définie par :
Milieux dilués[modifier | modifier le code]
| Matériau | n |
|---|---|
| Vide | 1 |
| Gaz à 0 °C et 1 atm | |
| Air | 1,000 293 |
| Hélium | 1,000 036 |
| Hydrogène | 1,000 132 |
| Dioxyde de carbone | 1,000 45 |
| Liquides à 20 °C | |
| Eau | 1,333 |
| Éthanol | 1,36 |
| Huile d'olive | 1,47 |
| Solides | |
| Glace | 1,309 |
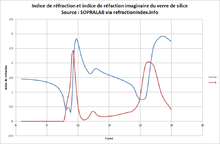
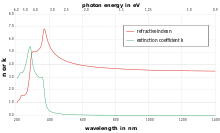
| Silice fondue (quartz) | 1,46[17] |
| PMMA (Plexiglas) | 1,49 |
| Verre à vitre | 1,52 |
| Verre crown (typique) | 1,52 |
| Polycarbonate (Lexan) | 1,58[18] |
| Verre flint (typique) | 1,66 |
| Saphir | 1,77[19] |
| Zircone cubique | 2,15 |
| Diamant | 2,417 |
| Moissanite | 2,65 |
Seuls les milieux dilués, c'est-à-dire les gaz, présentent des caractéristiques qui permettent un calcul aisé avec peu d'approximations de l'indice de réfraction. Les milieux dilués ayant des molécules très espacées, il est en effet possible de négliger les interactions des charges entre elles et supposer que seule l'interaction entre les charges et le champ incident compte[20].
Si on note N le nombre de dipôles électriques auxquels sont assimilées les électrons des atomes du gaz. Les protons, trop lourds, ne sont pas mis en vibration par les ondes lumineuses et seuls les électrons interagissent, menant à cette approximation des dipôles électriques. On considère que l'indice est proche de 1 et que le champ résultant est la somme du champ incident et du champ généré par les dipôles oscillants qui est la solution d'une équation différentielle harmonique amortie.
L'indice dans un milieu dilué correspond à , où :
- q est la charge de la particule mise en mouvement oscillant par le champ (le plus souvent donc la charge d'un électron) ;
- ε0 la permittivité diélectrique du vide ;
- m la masse de la charge ;
- ω et ω0 la fréquence de l'onde et la fréquence angulaire propre de l'électron pour l'atome : elle correspond à une des bandes d'absorption du matériau[21] ;
- γ est un coefficient phénoménologique correspondant à une dissipation d'énergie.
Indice de réfraction dans certains métaux[modifier | modifier le code]
Acier: 2,5
Aluminium: 1,44
Bronze: 1,18
Cuivre: 1,1
Plomb: 2,1
Indice de groupe[modifier | modifier le code]
À l'image de l'indice de réfraction calculé à partir de la vitesse de phase d'une onde monochromatique, on parle aussi d'indice de groupe pour l'indice de réfraction calculé à partir de la vitesse de groupe d'un paquet d'onde. Utilisé pour les impulsions courtes et les impulsions réelles qui ne sont jamais parfaitement monochromatiques, l'indice de groupe s'écrit comme suit[22],[W 1] :
Variations de l'indice de réfraction[modifier | modifier le code]
L'indice de réfraction est une grandeur caractérisant une interaction entre lumière et matière, ainsi elle est intrinsèquement dépendante des caractéristiques du milieu et de l'onde électromagnétique incidente.
L'indice d'un milieu dépend des paramètres qui caractérisent le milieu : température, pression, densité, etc. Les contraintes mécaniques imposées à un matériau transparent modifient également son indice. La conséquence de cette contrainte est généralement l'apparition d'une biréfringence liée à l'anisotropie qui en résulte (biréfringence induite). Ceci est utilisé pour étudier expérimentalement certaines structures mécaniques par photoélasticimétrie.
Dépendance à la longueur d'onde[modifier | modifier le code]

La valeur de l'indice dépend de la longueur d'onde du rayon lumineux incident. Ce phénomène appelé dispersion a été approché à l'aide de multiples formules empiriques mais il n'existe pas de formule précise permettant de déterminer l'indice en fonction de la longueur d'onde quel que soit le matériau.
La dispersion a pour effet que la réfraction est plus ou moins forte selon la longueur d'onde de la lumière, c'est ce qui provoque la décomposition de la lumière par un prisme mais aussi les aberrations chromatiques dans les instruments d'optique. Dans le premier cas le prisme ne réfracte pas toutes les couleurs de la lumière blanche au même angle, et la lumière qui sort est donc décomposée pour former le spectre visible. Dans le second cas, il s'agit du fait qu'un système optique est le plus souvent optimisé pour quelques longueurs d'onde particulières. Les pièces du système cependant dispersent la lumière et ainsi, le système ne sera pas parfaitement optimisé pour toutes les longueurs d'onde.
Étant donné cette dépendance, une convention répandue pour les milieux transparents dans le spectre visible veut que l'on donne l'indice de réfraction du milieu pour la longueur d'onde de la raie d du sodium (soit 587,56 nm), ou la raie e du mercure (à 546,07 nm)[W 2].
La variation de l'indice de réfraction d'un milieu transparent dans le spectre visible est appelée dispersion ; elle est caractérisée par le coefficient de dispersion ou nombre d'Abbe :
F et C désignant deux raies de l'hydrogène à respectivement 486,1 nm et 656,3 nm.
Plusieurs modèles de dispersion existent pour les milieux dans des domaines différents du spectre électromagnétique, notamment la formule de Cauchy :
valable pour les matériaux dont les bandes d'absorption sont dans le domaine ultraviolet, la formule de Briot
pour les matériaux dont une bande d'absorption se trouve dans l'infrarouge et les autres dans l'ultraviolet (comme l'eau)[24], et enfin la formule de Sellmeier
- .
Ces lois empiriques déterminées grâce à des mesures très précises de la longueur d'onde s'appliquent aux milieux transparents à la lumière visible. Les modèles sont établis en considérant qu'étant loin des bandes d’absorption, il est possible de considérer l'indice comme réel (pas de facteur d'atténuation) et d'établir un développement limité de l'indice en fonction de la longueur d'onde. Ces formules sont précises en général à la cinquième décimale près[24].
La dispersion est intrinsèquement liée au principe de l'indice de réfraction, qui résulte de la polarisation des électrons d'un milieu par une onde incidente. Chaque onde possédant une longueur d'onde donnée et donc une énergie donnée, va de ce fait polariser plus ou moins fortement les électrons. Le milieu réagit alors différemment selon la longueur d'onde incidente.
Dépendance à la température et la pression[modifier | modifier le code]
L'indice de réfraction d'un gaz varie proportionnellement à sa masse volumique. Il suit la loi dite loi de Gladstone qui est :
- [25].
Cette formule découle de la formule de Lorentz-Lorenz ou formule de Clausius-Mossotti, dont l'énoncé est où N est le nombre de molécules par unité de volume, α la polarisabilité d'une molécule et est la permittivité diélectrique du vide. Lorsque l'indice est très proche de 1 comme c'est le cas pour les gaz, il est possible d'en déduire que montrant une dépendance de l'indice de réfraction à la température et à la pression. La formule n'est valable que pour les gaz, mais les déductions quant à la dépendance de l'indice à la pression et la température peuvent s'étendre aux solides et aux liquides[26].
Dépendance à la direction de propagation[modifier | modifier le code]
Certains matériaux n'ont pas un indice de réfraction isotrope : il dépend alors de la direction de propagation et de l'état de polarisation de la lumière.
Lorsque le matériau présente deux indices de réfraction différents selon deux axes la différence de ces indices est nommée biréfringence. On trouve ce genre de comportement dans les cristaux anisotropes mais aussi dans les verres optiques soumis à des contraintes particulières.
Les cristaux dit biaxes, à symétrie orthorhombique, monoclinique et triclinique possèdent trois indices de réfraction typiques, notés le plus souvent x, y et z ou α, β et γ, ou encore Ng (le plus grand), Np (le plus petit), et Nm (intermédiaire). La représentation de l'indice de réfraction selon ses directions dans le cristal forme un ellipsoïde[27], dont les trois indices sont les axes orthogonaux.
Lorsque l'ellipsoïde possède deux axes de dimension identique, (c'est-à-dire que Nm est égal soit à Ng soit à Np), il présente une symétrie de révolution autour de l'axe dit "axe optique", et le cristal est dit uniaxe. L'indice de réfraction est dit ordinaire, no, pour les rayons polarisés à 90° de l'axe optique du cristal, formant ainsi le rayon lumineux ordinaire, et l'indice est dit extraordinaire pour les rayons polarisés selon l'axe optique du cristal, ne.
Il est par ailleurs possible d'engendrer de la biréfringence de manière artificielle, sans que le matériau possède des axes de symétrie particuliers. L'effet Kerr électrooptique va générer ainsi deux indices de réfraction, parallèle et perpendiculaire au champ électrique qui est imposé[28]. Les propriétés élasto-optiques des matériaux permettent aussi de décrire le comportement de la biréfringence induite par une contrainte mécanique : l'indice de réfraction est alors différent entre l'axe parallèle au vecteur de pression et le plan perpendiculaire à ce vecteur[29].
Indice de réfraction de l'air[modifier | modifier le code]
L'indice de réfraction de l'air a fait l'objet de multiples études : il présente une importance capitale pour toute étude et mesure portant sur l'atmosphère ou sur tout phénomène soumis à celle-ci. Sa valeur dépend de nombreux paramètres et a fait l'objet de mesures et de formules dont la précision est très variable. La première approche effectuée sur la réfrangibilité de l'air est effectuée au XVIIIe siècle par Isaac Newton qui relève en 1625[30] les altitudes apparentes et les angles de réfraction des étoiles au travers de l'atmosphère, amenant Edmond Halley à publier ces résultats en 1721 pour illustrer la réfrangibilité de l'air[A 2]. Plus tard François Arago et Jean-Baptiste Biot estiment la valeur de l'indice en 1806[W 3].
La première véritable formule établissant l'indice de l'air est composée par H. Barrell et J. E. Sears en 1938. Nommée formule de Barrell et Sears, elle a la forme d'une formule de Cauchy à deux termes en λ−2 et λ−4. Désormais obsolète, elle continue cependant d'être utilisée[W 3],[A 3].
Deux formules plus récentes désormais très employées donnent une meilleure approximation de l'indice de l'air : celle de Philip E. Ciddór[A 4] et celle d'Edlén[A 5],[W 3]. Les formules prennent en compte plus ou moins de facteurs, notamment la présence de vapeur d'eau, de dioxyde de carbone et sont valables sur une étendue plus ou moins grande de longueurs d'onde.
L'indice de réfraction de l'air peut être mesuré de manière très précise grâce à des méthodes interférométriques, jusqu'à un ordre de 10−7 ou moins[31]. Il est d’environ 1,000293 à 0 °C et 1 atm[32]
Spectre visible et infrarouge[modifier | modifier le code]
Une formulation de l'indice de l'air, valable sous certaines conditions définies, fut approuvée par la Commission conjointe pour la spectroscopie (Joint Commission for Spectroscopy) à Rome en , comme suit[31] :
- .
Cette formule est valable pour des longueurs d'onde allant de 0,2 µm à 1,35 µm (visible et infrarouge) dans de l'air sec contenant 0,03 % de CO2 par volume à 15 °C et 101,325 kPa (soient 760 Torr).
Co-indice de réfraction[modifier | modifier le code]
Pour les hyperfréquences et les ondes radio, la composition de l'air est très importante. Dans l’ionosphère, les électrons libres ont un effet dispersant sur les ondes électromagnétiques. Dans la troposphère, la teneur en vapeur d'eau et eau liquide change grandement l'indice de réfraction. Le tout est modulé par la température et la pression. On définit comme le co-indice N pour ces fréquences. Il s'exprime ainsi car c'est l'ordre de variation de entre l'espace et la surface terrestre.
N est relié aux paramètres d'environnement par la formule expérimentale suivante[A 6],[33] :
Le premier terme s'applique dans toute l'épaisseur de l'atmosphère, le second est important dans la troposphère et le troisième dans l'ionosphère. Il est donc possible de mesurer la variation de N quand on connaît ne, P, e et T ; et vice versa. Cette formule est très utilisée dans le calcul du délai causé par l'atmosphère sur le signal d'un satellite dans le système de positionnement par satellites (GPS), dans celui du calcul du parcours d'un faisceau radar, dans l'utilisation d'un réfractomètre hyperfréquence et dans bien d'autres domaines.
Milieux d'indice de réfraction inférieur à l'unité[modifier | modifier le code]
Les milieux « naturels » possèdent des indices bornés par l'indice du vide, qui est l'unité. Cependant les recherches en laboratoire, notamment sur les métamatériaux à indice de réfraction négatif (en) et les cristaux photoniques ont permis d'engendrer des phénomènes électromagnétiques conférant des indices inférieurs à 1. Les métamatériaux à indice de réfraction négatifs sont un certain type de métamatériaux dans lesquels la réfraction produit une onde réfractée du même côté de la normale que l'onde incidente, assimilant l'indice de réfraction du milieu à un indice négatif. Il existe aussi un autre phénomène impliquant ces métamatériaux, mais aussi les cristaux photoniques : l'ultraréfraction, où une onde se propageant dans le vide, incidente sur un milieu va être réfractée à un angle plus grand que l'angle d'incidence, assimilant l'indice de réfraction du milieu à un indice positif mais inférieur à 1.
Ultra-réfraction[modifier | modifier le code]
On parle d'ultra-réfraction pour le phénomène ayant lieu dans un milieu dont l'indice est compris entre 0 et 1[A 7].
Réfraction négative[modifier | modifier le code]
On parle de réfraction négative pour le phénomène ayant lieu dans un milieu dont l'indice est inférieur à 0[A 7].
Indice de réfraction non linéaire[modifier | modifier le code]
C'est avec l'apparition du laser que sont découverts les premiers effets non linéaires en optique. L'indice de réfraction résultant d'une interaction entre la lumière et le milieu, celle-là provoquant une polarisation locale de celui-ci, en présence de fortes puissances incidentes, le régime de fonctionnement va s'éloigner de la linéarité. L'indice de réfraction devient alors dépendant de l'intensité de l'onde incidente : où n0 est l'indice de réfraction linéaire, valable pour les intensités moyennes et faibles et γ est le coefficient d'indice non linéaire[34].
La modification de l'indice de réfraction avec l'intensité du champ électrique est souvent nommé effet Kerr optique par analogie avec l'effet Kerr électro-optique où la modification de l'indice est proportionnelle à la puissance du champ électrostatique appliqué au milieu. Il est possible de trouver une expression de l'indice de réfraction non linéaire en observant la polarisabilité d'un matériau sachant que . La polarisation totale, linéaire et non linéaire, du milieu se décrit ainsi :
- ,
où P est la polarisation, χ le tenseur de susceptibilité électrique dont la partie non linéaire est le tenseur χ(3), E le champ électrique, et ε0 la permittivité diélectrique du vide. Comme et on déduit :
Or dans le domaine linéaire, l'indice de réfraction peut s'écrire , soit ici . On en déduit :
[35].
Les phénomènes résultants de la dépendance de l'indice de réfraction à l'intensité lumineuse sont entre autres l'autofocalisation, l'automodulation de phase, la conjugaison de phase et la génération de solitons optiques[36].
Ces problèmes très complexes d'optique non linéaire se limitent cependant aux milieux soumis à des ondes lumineuses d'intensité très fortes et aux caractéristiques intrinsèques favorables à la non-linéarité.
Mesure de l'indice de réfraction[modifier | modifier le code]


Parmi les instruments de métrologie optique, plusieurs peuvent être utilisés à des fins de mesure de l'indice de réfraction. On trouve, entre autres, parmi ces instruments les réfractomètres, qui sont un type d'interféromètre, les goniomètres, certains prismes, etc. Ces méthodes sont pertinentes pour le domaine de transparence des matériaux.
La mesure par prisme en V consiste à placer un échantillon de l'élément transparent dans la partie en toit inversé d'un bloc de verre dont on connaît précisément l'indice. La déviation du faisceau de lumière permet de déterminer l'indice de réfraction de l'échantillon[W 2].
Le goniomètre permet pour de multiples raies spectrales de mesurer l'indice de réfraction d'un matériau transparent. Un prisme de ce matériau est utilisé pour en mesurer l'angle de déviation minimal à plusieurs longueurs d'onde[W 2].
Le réfractomètre est un type d'interféromètre dont un « bras » est plongé dans le vide et un autre dans le matériau à mesurer[37].
L'inconvénient des méthodes interférométriques est qu'elles sont difficilement utilisables sur des objets manufacturés et peut se révéler destructive puisqu'il est nécessaire de mesurer un échantillon à la géométrie bien définie, excluant ainsi les verreries artistiques par exemple. Dans ces cas la mesure des angles de réfraction, de l'angle de Brewster ou encore la recherche d'un liquide d'indice équivalent par application sur les imperfections sont utilisées mais ne permettent en général pas d'atteindre des précisions aussi bonnes que pour les mesures au goniomètre ou à l'interféromètre[38].
Pour les liquides le réfractomètre le plus utilisé est le réfractomètre d'Abbe basé sur le principe de la mesure de l'angle de réfraction limite et permettant d'atteindre des précisions de l'ordre de ± 0,000 2[39],[40].
Comme la mécanique quantique prévoit que les particules peuvent se comporter comme des ondes, il est aussi possible de mesurer l'indice de réfraction des ondes de matière. Une telle mesure a été réalisée notamment sur les atomes de lithium et de sodium, à l'aide d'une méthode interférométrique[A 8].
L'indice de réfraction non linéaire est mesurable par observation du décalage de la phase du faisceau lumineux test par modulation croisée (en) (XPM) mais aussi grâce à la rotation de polarisation elliptique, l'analyse du profil spectral de l'onde ou encore l'analyse spectrale en automodulation de phase ou remonter à l'indice non linéaire par la détermination de la puissance critique d'autofocalisation. Il est aussi possible de mesurer l'indice par de l'interférométrie spectrale des supercontinuums[41].
La mesure de l'indice de groupe permet de mesurer le chemin optique de la lumière et donc la longueur d'une fibre optique. Une technique de mesure de l'indice de groupe est la réflectométrie à basse cohérence optique[N 3],[42]
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Huyghens se base par ailleurs sur la théorie ondulatoire de la lumière, alors sujette à controverse et décriée par rapport à la théorie particulaire.
- De Handbook of optics 2009, p. 7.13 : « it is a macroscopic manifestation of the microscopic response of matter to a periodic driving force. »
- Traduction du terme anglais : (en)Optical Low Coherence Reflectometry
Références[modifier | modifier le code]
Livres[modifier | modifier le code]
- Jean-Marie Blondeau et Monique Vindevoghel, « Dioptre plan: indice de réfraction », sur unisciel.fr : Université en Ligne, (consulté le )
- Smith 1996, p. 42-45
- Benson 2009, p. 111
- Rashed 1997
- Bécherrawy 2005, p. 38
- Chartier 1997, p. 423
- Giancoli 1993, p. 78-79
- William 2002, p. 62
- Benson 2009, p. 132
- Chartier 1997, p. 424-427
- (en) Richard P. Feynman, Mainly Mechanics, Radiation, and Heat, vol. 1, Basic Books, coll. « Feynman Lectures on Physics », (ISBN 978-0-465-02493-3)
- Taillet 2006, p. 216
- Handbook of optics 2009, p. 7.13
- Chartier 1997, p. 431
- Chartier 1997, p. 429
- Born et Wolf 1993, p. 14
- (en) Malitson, « Refractive Index Database », sur refractiveindex.info, (consulté le )
- (en) N. Sultanova, S. Kasarova et I. Nikolov, « Dispersion Properties of Optical Polymers », Acta Physica Polonica A, vol. 116, no 4, , p. 585–587 (DOI 10.12693/APhysPolA.116.585
 , Bibcode 2009AcPPA.116..585S)
, Bibcode 2009AcPPA.116..585S)
- (en) J. Tapping et M. L. Reilly, « Index of refraction of sapphire between 24 and 1060°C for wavelengths of 633 and 799 nm », Journal of the Optical Society of America A, vol. 3, no 5, , p. 610 (DOI 10.1364/JOSAA.3.000610, Bibcode 1986JOSAA...3..610T, lire en ligne)
- Chartier 1997, p. 425-427
- Chartier 1997, p. 46
- Maciejko 2002, p. 65
- Maciejko 2002, p. 73
- Chartier 1997, p. 437
- Bécherrawy 2005, p. 177
- Chartier 1997, p. 432
- Weber 2002, p. 4
- Weber 2002, p. 251
- Weber 2002, p. 253
- Gjertsen 1986, p. 432
- Bach et Neuroth 1998, p. 97
- (en) Optics, 4e éd., Pearson Higher Education, (ISBN 978-0-321-18878-6)
- Bevis et al. 1994
- Barton et Guillemet 2005, p. 117
- Boyd 2008, p. 207-208
- Boyd 2008, p. 329-375
- //books.google.com/books?id=cxOvPNnkMEsC&pg=PA6
- Dufrenne, Maës et Maës 2005, p. 443
- Aminot et Kérouel 2004, p. 79
- Denis, Briant et Hipeaux 1997, p. 129
- Wilkes 2007, p. 7
- //books.google.com/books?id=gc5KtfYCu7MC&pg=PA65
Articles scientifiques[modifier | modifier le code]
- Itard 1957
- Halley 1720, p. 169-172
- Barrell et Sears 1939
- Ciddór 1996, p. 1566-1573
- Edlén 1966
- Fabry, Frush et Kilambi 1997
- Maystre 2003
- Jacquey et al. 2007, p. 240405
Sites web[modifier | modifier le code]
- (en) « Group index », sur RP Photonics
- (en)[PDF]« Refractive index and dispersion », Technical information, sur Schott AG, (consulté le )
- (en) « Refractivity of air » (consulté le )
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
Cette liste contient l'ensemble des sources utilisées comme référence. Leur lecture permet d'approfondir le sujet et détailler les méthodes et calculs de l'article.
Ouvrages en français[modifier | modifier le code]
- Harris Benson (trad. de l'anglais), Physique : 3, Ondes, optique et physique moderne, Bruxelles/Paris/Saint-Laurent (Québec), De Boeck, coll. « De Boeck Supérieur », , 4e éd., 544 p. (ISBN 978-2-8041-0763-5, lire en ligne)
- Tamer Bécherrawy, Optique géométrique, Bruxelles, De Boeck, coll. « De Boeck Supérieur », , 404 p. (ISBN 2-8041-4912-9, lire en ligne)
- Tobin William (trad. de l'anglais par James Lequeux), Léon Foucault : le miroir et le pendule, Les Ulis, EDP Sciences, coll. « Sciences et Histoire », , 354 p. (ISBN 2-86883-615-1, lire en ligne)
- Douglas C. Giancoli (trad. François Gobeil), Physique générale 3 : Ondes, optique et physique moderne, De Boeck, coll. « De Boeck Supérieur », , 504 p. (ISBN 2-8041-1702-2, lire en ligne)
- Richard Taillet, Optique physique : Propagation de la lumière, Bruxelles/Paris, De Boeck, coll. « De Boeck Supérieur », , 323 p. (ISBN 2-8041-5036-4, lire en ligne)
- Germain Chartier, Manuel d'optique, Paris, Hermès, , 683 p. (ISBN 2-86601-634-3)
- James L. Barton et Claude Guillemet, Le verre, science et technologie, Les Ulis, EDP Sciences, , 440 p. (ISBN 2-86883-789-1, lire en ligne)
- Roland Dufrenne, Jean Maës et Bernard Maës, La Cristallerie de Clichy : Une prestigieuse manufacture du XIXe siècle, Clichy-la-Garenne, La Rose de Clichy, , 447 p. (ISBN 2-9522492-0-2, lire en ligne)
- Alain Aminot et Roger Kérouel, Hydrologie des écosystèmes marins : paramètres et analyses, Éditions Quae, , 335 p. (lire en ligne)
- Jacques Denis, Jean Briant et Jean-Claude Hipeaux, Physico-chimie des lubrifiants : Analyses et essais, Éditions OPHRYS, , 432 p. (lire en ligne)
- Romain Maciejko, Optoélectronique, Montréal, Presses internationales polytchniques, , 528 p. (lire en ligne)
- Roshdi Rashed, Histoire des sciences arabes : Mathématiques et physique, vol. 2, Seuil,
Ouvrages en anglais[modifier | modifier le code]
- (en) A. Mark Smith, Ptolemy's Theory of visual perception, vol. 86, Transactions of the American Phylosophical Society, , partie 2
- (en) Optical Society of America, Handbook of optics, vol. I à V, McGraw-Hill Professional, , 3e éd., 5600 p. (ISBN 978-0-07-170160-0, lire en ligne)
- (en) Max Born et Emil Wolf, Principles of optics : Electromagnetic theory of propagation interference and diffraction of light, Oxford/New York/Beijing etc., Pergamon Press, , 6e éd., 808 p. (ISBN 0-08-026482-4 et 0-08-026481-6)
- (en) Marvin J. Weber et al. (préf. Marvin J. Weber), Handbook of Optical Materials, Boca Raton, CRC Press, , 536 p. (ISBN 0-8493-3512-4 et 978-0849335129, présentation en ligne)
- (en) Derek Gjertsen, The Newton Handbook, Taylor & Francis, , 665 p. (lire en ligne)
- (en) Hans Bach et Norbert Neuroth, The properties of optical glass, Berlin, Springer, , 2e éd., 419 p. (ISBN 3-540-58357-2, lire en ligne)
- (en) Robert W. Boyd, Nonlinear Optics, Burlington, MA, Academic Press, , 3e éd., 640 p. (ISBN 978-0-12-369470-6, lire en ligne)
- (en) Zachary W. Wilkes, Investigation of the Nonlinear Index of Refraction of Water at 815 and 407 Nanometers, ProQuest, , 97 p. (lire en ligne)
Articles de revues à comité de lecture[modifier | modifier le code]
- Jean Itard, « Les lois de la réfraction de la lumière chez Kepler », Revue d'histoire des sciences et de leurs applications, vol. 10, no 1, , p. 59-68 (lire en ligne)
- (en) Edmond Halley, « Some remarks on the allowances to be made in astronomical observations for the refraction of the air », Philosophical transactions, vol. 31, nos 364-369, (JSTOR 103416)
- (en) H. Barrell et J. E. Sears, « The Refraction and Dispersion of Air for the Visible Spectrum », Philosophical transactions of the Royal Society A, vol. 238,
- (en) Philip E. Ciddór, « Refractive index of air:new equations for the visible and near infrared », Applied optics, Optical society of America, vol. 35, no 9, , p. 1566-1573 (lire en ligne)
- (en) Bengt Edlén, « The Refractive Index of Air », Metrologia, vol. 71, no 2, (DOI 10.1088/0026-1394/2/2/002, résumé)
- (en) M. Jacquey, M. Büchner, G. Trénec et J. Vigué, « First measurements of the index of refraction of gases for lithium atomic waves », Physical Review Letters, vol. 98, no 24, , p. 240405
- (en) D. Maystre, « Electromagnetic analysis of ultra-refraction and negative refraction », Journal of Modern Optics, Taylor and Francis, vol. 50, no 9, , p. 1431-1444 (DOI 10.1080/09500340308235216)
- (en) F. Fabry, C. Frush, I. Zawadzki et A. Kilambi, « Extracting near-surface Index of refraction using radar phase measurements from ground targets », Journal of Atmospheric and Oceanic Technology, American Meteorological Society, no 14, , p. 978-987 (DOI 10.1109/APS.1997.625552, lire en ligne)
- (en) M. Bevis, S. Businger, S. Chiswell, T. A. Herring, R. A Anthes, C. Rocken et R. H. Ware, « GPS Meteorology: mapping zenith wet delay onto precipitable water », J. Appl. Meteorol., vol. 33, , p. 379–386 (DOI /10.1175/1520-0450%281994%29033%3C0379%3AGMMZWD%3E2.0.CO%3B2, lire en ligne [PDF], consulté le )










































