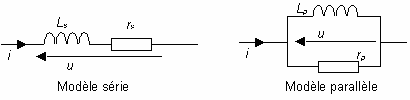Bobine (électricité)
Une bobine, bobine d'inductance[1], solénoïde, auto-inductance, self-inductance[2] ou quelquefois self (par anglicisme)[3] est un composant courant en électrotechnique et électronique. Une bobine est constituée d'un enroulement de fil conducteur éventuellement autour d'un noyau en matériau ferromagnétique qui peut être un assemblage de feuilles de tôle ou un bloc de ferrite. Les physiciens et ingénieurs français[1] l'appellent souvent par synecdoque « inductance », ce terme désignant la propriété caractéristique de la bobine, qui est son opposition à la variation du courant dans ses spires.


Un circuit inducteur est caractérisé par son inductance, qui est le rapport entre la tension et le taux de variation du courant. Dans le Système international d'unités (SI), l'unité d'inductance est le henry (H), du nom du scientifique américain du XIXe siècle, Joseph Henry. Dans la mesure des circuits magnétiques, c'est l'équivalent du weber/ampère. Les inductances ont des valeurs qui vont généralement de 1 µH (10-6 H) à 20 H. De nombreuses inductances ont un noyau magnétique en fer ou en ferrite à l'intérieur de la bobine, qui sert à augmenter le champ magnétique et donc l'inductance. Avec les condensateurs et les résistances, les bobines d'inductance sont l'un des trois éléments linéaires passifs qui composent les circuits électroniques. Les bobines d'inductance sont largement utilisées dans les équipements électroniques à courant alternatif (AC), en particulier dans les équipements radio. Elles peuvent être utilisées pour bloquer le courant alternatif tout en laissant passer le courant continu, les inductances conçues à cette fin sont appelées bobine d'arrêt[4]. Elles sont également utilisées dans les filtres électroniques pour séparer les signaux de différentes fréquences, et en combinaison avec des condensateurs pour réaliser des circuits LC, utilisés pour ajuster les récepteurs de radio et de télévision.
Description[modifier | modifier le code]
La partie la plus visible est un enroulement de fils conducteurs.
L'espace au milieu de ces spires s'appelle le noyau. Il peut être vide ou inclure une pièce en matériau ferromagnétique favorisant l'induction électromagnétique, afin d'augmenter la valeur de l'inductance. Le noyau peut être un circuit magnétique complètement ou partiellement fermé pour améliorer la linéarité de l'inductance.
Le circuit magnétique d'une bobine avec noyau peut être « saturé » si l'on essaye d'induire un flux supérieur à la valeur limite acceptable par le noyau ; à ce moment, la valeur de l'inductance de la bobine s'effondre. Pour augmenter la réluctance de la bobine et retarder la saturation, on peut aménager une ouverture, appelée entrefer, dans le noyau.
Un entrefer est indispensable au fonctionnement des têtes de lecture/écriture des appareils tels que : magnétophone à bande magnétique, disque dur d'ordinateurs, etc.
Applications[modifier | modifier le code]


Les bobines d'inductance sont largement utilisées dans les circuits analogiques et le traitement des signaux. Les applications vont de l'utilisation de grandes inductances dans les alimentations, qui, associées à des condensateurs de filtrage, éliminent de la sortie en courant continu l'ondulation qui est un multiple de la fréquence du réseau (ou de la fréquence de commutation pour les alimentations à découpage), à la petite inductance de la perle ou du tore de ferrite installé autour d'un câble pour empêcher la transmission des interférences radioélectriques le long du fil. Les inductances sont utilisées comme dispositif de stockage d'énergie dans de nombreuses alimentations à découpage pour produire du courant continu. La bobine d'inductance fournit de l'énergie au circuit pour maintenir le courant pendant les périodes de commutation "off" et permet des topographies où la tension de sortie est supérieure à la tension d'entrée.
On trouve des bobines, souvent en combinaison avec d'autres composants électroniques, dans une grande variété de dispositifs :
- Pour créer une impulsion de haute tension nécessaire :
- bobine d'allumage : dans les moteurs à allumage commandé, l'ouverture du circuit primaire par le rupteur déclenche une élévation importante de la tension dans le circuit secondaire de la bobine, et la production d'une étincelle au niveau des électrodes des bougies, permettant la mise en combustion du mélange air-essence dans les cylindres ;
- dans les systèmes de clôture électrique utilisant un rupteur et une bobine, similaire au système utilisé dans les moteurs à allumage commandé, pour engendrer une haute tension, mais de faible intensité qui, dans les fils de clôture, dissuade le bétail de s'en approcher ;
- à l'amorçage d'une lampe à décharge (par exemple tube fluorescent) : le ballast, (souvent une bobine, un rupteur et un condensateur en série), constitue un circuit résonant qui crée une surtension à chaque alternance après la mise sous tension, jusqu'à ce que le passage du courant dans le gaz du tube l'amortisse le circuit ; il limite ensuite l'intensité du courant dans le tube.
- Pour leurs propriétés électromagnétiques[a] :
- électroaimants ;
- relais électromécaniques utilisant généralement un solénoïde ;
- actionneurs ou actuateurs linéaires ;
- moteurs électriques.
- Pour le lissage d'un courant électrique ou le filtrage d'un signal électrique ou d'une tension d'alimentation :
- réduction de l'ondulation résiduelle après le redressement dans les locomotives à hacheur lorsque le Filtre actif ne peut être employé;
- réduction de l'ondulation résiduelle après le redressement de la haute tension d'alimentation (dans les appareils à tubes) ;
- réduction des tensions haute fréquence parasites sur une ligne d'alimentation ou une entrée d'appareil (ferrite, bobine d'arrêt) ;
- filtrage de signaux bas niveaux (en raison de difficultés d'emploi des bobines, on préfère souvent pour les mêmes fonctions des filtres actifs qui n'en emploient pas[b] ;
- filtrage des alimentations (les bobines avaient disparu des alimentations pour les mêmes raisons que pour le filtrage du signal quand les alimentations linéaires à transistors se sont généralisées, mais elles sont essentielles pour les alimentations à découpage qui remplacent, depuis une époque plus récente, les alimentations linéaires).

- Pour constituer des circuits résonants[c], on utilise souvent des bobines à inductance ajustable. Par exemple :
- réglage de l'accord haute fréquence du récepteur de radio à celle de l'émetteur que l'on souhaite recevoir ;
- réglage de la fréquence d'un oscillateur.
- Pour accorder l'impédance d'un circuit :
- pour minimiser les pertes dans une ligne téléphonique au moyen de bobines de charge (de nos jours, on utilise le plus souvent des répéteurs actifs)[d] ;
- en série (bobine de charge) avec une antenne pour ajuster sa longueur électrique ;
- ou en parallèle avec des condensateurs créer des trappes dans une antenne de façon qu'elle puisse servir pour plusieurs bandes de fréquences[5].
- Des systèmes de régulation magnétique utilisent la non-linéarité de l'inductance au niveau de la saturation du noyau.
Les bobines sont fondamentales dans les alimentations à découpage qui permettent le branchement des appareils sur les types de courant alternatif existant dans le monde entier, ainsi que la conversion continu-continu. Les alimentations Flyback sont un type plus ancien utilisant (comme pour l'allumage des moteurs) une accumulation d'énergie nommée accumulation inductive[6].
Des dispositifs similaires aux alimentations à découpage se trouvent dans :
- les flashs électroniques, pour la charge du condensateur de stockage de l'énergie utile pour produire l'éclair, à partir de piles ou d'accumulateurs ;
- les armes fonctionnant par choc électrique ;
- certaines grilles de désinsectisation fonctionnant avec une haute tension.
Des bobines en supraconducteur servent pour le stockage d'énergie sous forme électromagnétique dans les dispositifs SMES (Superconducting Magnet Energy Storage).
Deux inductances (ou plus) à proximité qui ont un flux magnétique couplé (inductance mutuelle) forment un transformateur, qui est un composant fondamental de tout réseau électrique. L'efficacité d'un transformateur peut diminuer lorsque la fréquence augmente en raison des courants de Foucault dans le matériau du noyau et de l'effet de peau sur les enroulements. La taille du noyau peut être réduite à des fréquences plus élevées. Pour cette raison, les avions utilisent un courant alternatif de 400 hertz plutôt que les 50 ou 60 hertz habituels, ce qui permet un grand gain de poids grâce à l'utilisation de transformateurs plus petits[7]. Les transformateurs permettent des alimentations à découpage qui isolent la sortie de l'entrée.
Les bobines d'inductance ont des effets parasites qui les font s'écarter du comportement idéal. Elles créent et subissent des interférences électromagnétiques (EMI). Leur taille physique les empêche d'être intégrées sur les puces à semi-conducteurs. L'utilisation des bobines d'inductance est donc en déclin dans les appareils électroniques modernes, notamment les appareils portables compacts. Les inductances réelles sont de plus en plus remplacées par des circuits actifs tels que le gyrateur (en) qui permet de synthétiser l'inductance à l'aide de condensateurs.
Le dipôle bobine[modifier | modifier le code]


Pour raisonner sur les circuits électroniques et calculer les valeurs nécessaires, on considère des objets idéaux, qui n'ont que les caractéristiques nécessaires au rôle que l'on veut leur faire jouer. Une bobine est considérée, dans ce cadre, comme un dipôle présentant une inductance pure. Si les autres caractéristiques, comme la résistance du fil de la bobine ou la capacité entre spires ne sont pas négligeables, on les représente sous la forme d'autres composants, non moins idéaux, séparés.
Les défauts de linéarité compliquent grandement les calculs. En général, on se limite à un domaine où les caractéristiques des composants sont approximativement linéaires. Il faut donc au moins connaître les limites de ce domaine, dont on peut, cependant, être amené à sortir, comme on peut exploiter, dans certaines applications, les non-linéarités.
Pertes dans une bobine réelle[modifier | modifier le code]
Une bobine ne présente jamais une inductance propre pure. Les pertes peuvent provenir de plusieurs causes[8] :
- résistance ohmique du fil enroulé autour du noyau, accrue du fait de l'effet de peau dans le bobinage à partir de quelques centaines de kHz ;
- pertes par hystérésis proportionnelles à la fréquence du courant qui traverse la bobine ;
- perte par courants de Foucault proportionnelles au carré de la fréquence du courant qui traverse la bobine.
De plus, les capacités entre spires ne sont pas négligeables à haute fréquence.
Modèles de la bobine réelle[modifier | modifier le code]
Modèles à deux dipôles[modifier | modifier le code]
Les modèles les plus simples et les plus fréquemment utilisés sont ceux correspondant à l'association d'une bobine d'inductance et d'une résistance :
| Modèle série | Modèle parallèle | |
|---|---|---|
| Équation |
En régime sinusoïdal de pulsation ω, les deux modèles précédents sont équivalents et interchangeables à condition de poser :
avec : facteur de qualité de la bobine pour la pulsation ω considérée.
Modèles à trois dipôles[modifier | modifier le code]
Aux modèles précédents, il est parfois nécessaire d'ajouter un condensateur en parallèle avec l'ensemble afin de rendre compte des effets capacitifs apparaissant entre les spires. Cette valeur de capacité est très faible mais elle devient prédominante à très grande fréquence (par exemple en VHF et UHF).
Relation entre la tension et l'intensité[modifier | modifier le code]
La tension aux bornes de la bobine et l'intensité du courant sont reliés par l'équation différentielle :
où :
- L est l'inductance de la bobine
- r sa résistance propre (dans le cas d'une bobine parfaite, r = 0).
Comportement d'une bobine soumise à un échelon de tension[modifier | modifier le code]
Lorsque la bobine est soumise brutalement à une tension constante E avec une résistance r en série, l'équation différentielle admet pour solution :
où :
- est la constante de temps de la bobine
Si on admet que les solutions de l'équation différentielle sont de la forme
où sont constantes et le temps écoulé, alors
et l'équation devient :
puis :
Pour vérifier cette équation, il faut que et puisque varie en fonction du temps.
On obtient alors :
B peut alors prendre une infinité de valeurs. Ainsi, si la bobine est en charge, d'où
ce qui permet de trouver la solution de l'équation différentielle en .
Démonstration usuelle : La solution de l'équation différentielle : est la somme de deux termes :
- , la solution du régime libre correspondant à l'équation sans second membre
- , la solution du régime forcé correspondant au régime établi quand toutes les dérivées sont nulles et donc solution de .
Solution du régime libre :
On intègre les deux membres
Si x = y alors :
donc :
Solution du régime forcé : Lorsque la bobine est soumise à un échelon de tension , la solution du régime forcé est :
Solution de l'équation :
La détermination de la constante est faite grâce à la condition physique suivante : Le courant à travers une inductance ne peut en aucun cas subir de discontinuité.
À l'instant , le courant vaut . On obtient l'équation :
Donc
Souvent, dans les cas d'école, le courant initial est nul. On obtient alors :
Comportement en régime sinusoïdal[modifier | modifier le code]
Pour obtenir les équations régissant le comportement d'une bobine réelle en régime sinusoïdal, il est nécessaire d'utiliser un des modèles décrit ci-dessus et de calculer l'impédance de la bobine soit en utilisant la représentation de Fresnel, soit en utilisant la transformation complexe.
Avec le modèle série, l'impédance de la bobine s'écrit :
ayant pour module :
- et pour argument :
Du fait de son caractère inductif, l'intensité du courant sinusoïdal qui traverse la bobine soumise à une tension sinusoïdale présente un retard de phase de 0 à 90° (soit 0 à π /2 radians) par rapport à la tension. On dit que le courant est en retard sur la tension[9].
Lorsque la bobine est réalisée autour d'un noyau ferromagnétique sans entrefer, les phénomènes de saturation magnétique et d'hystérésis entraînent des non-linéarités dans le comportement de la bobine : lorsqu'elle est soumise à une tension sinusoïdale, l'intensité du courant qui la traverse n'est pas purement sinusoïdal. Ces non-linéarités sont très difficiles à prendre en compte. Elles sont souvent négligées en première approximation dans les calculs traditionnels.
Analyse de circuit[modifier | modifier le code]
L'effet d'une inductance dans un circuit est de s'opposer aux variations du courant qui la traverse en développant une tension à ses bornes proportionnelle au taux de variation du courant. Une inductance idéale n'offrirait aucune résistance à un courant continu constant, cependant, seules les inductances supraconductrices ont une résistance électrique réellement nulle.
La relation entre la tension variable dans le temps v(t) aux bornes d'une inductance L et le courant variable dans le temps i(t) qui la traverse est décrite par l'équation différentielle :
Lorsqu'un courant alternatif (AC) sinusoïdal traverse une inductance, une tension sinusoïdale est induite. L'amplitude de la tension est proportionnelle au produit de l'amplitude (Ip) du courant et de la fréquence (f) du courant.
Dans cette situation, la phase du courant est en retard sur celle de la tension de π/2 (90°). Pour les sinusoïdes, lorsque la tension aux bornes de l'inducteur atteint sa valeur maximale, le courant s'annule, et lorsque la tension aux bornes de l'inducteur s'annule, le courant qui le traverse atteint sa valeur maximale.
Si une inductance est connectée à une source de courant continu de valeur I via une résistance R (au moins le DCR de l'inductance), puis que la source de courant est court-circuitée, la relation différentielle ci-dessus montre que le courant traversant l'inductance se décharge avec une décroissance exponentielle :
Réactance[modifier | modifier le code]
Le rapport entre la tension de crête et le courant de crête dans une inductance alimentée par une source de courant alternatif est appelé réactance et est noté XL.
Ainsi,
où ω est la fréquence angulaire.
La réactance est mesurée en ohms mais on parle d'impédance plutôt que de résistance. L'énergie est stockée dans le champ magnétique lorsque le courant augmente et est déchargée lorsque le courant diminue. La réactance inductive est proportionnelle à la fréquence. À basse fréquence, la réactance diminue ; en courant continu, l'inducteur se comporte comme un court-circuit. Plus la fréquence augmente, plus la réactance augmente et, à une fréquence suffisamment élevée, la réactance se rapproche de celle d'un circuit ouvert.
Fréquence de coupure[modifier | modifier le code]
Dans les applications de filtrage, par rapport à une impédance de charge particulière, une inductance a une fréquence de coupure définie comme suit :
Réseaux d'inductances[modifier | modifier le code]
Les inductances dans une configuration parallèle ont tous la même différence de potentiel (tension). Pour trouver leur inductance équivalente totale (Leq) :

Schéma de plusieurs inductances côte à côte, les deux fils de chacune des bobines étant connectés aux mêmes fils.
Le courant qui traverse les inductances en série reste le même, mais la tension aux bornes de chaque inductance peut être différente. La somme des différences de potentiel (tension) est égale à la tension totale. Pour trouver leur inductance totale :

Schéma de plusieurs inductances, connectées bout à bout (en série), avec la même quantité de courant passant à travers chacune d'entre elles.
Ces relations simples ne sont valables que lorsqu'il n'y a pas de couplage mutuel des champs magnétiques entre les différentes bobines d'inductance.
Inductance mutuelle[modifier | modifier le code]
L'inductance mutuelle se produit lorsque le champ magnétique d'une inductance induit un champ magnétique dans une inductance adjacente. L'induction mutuelle est la base de la construction des transformateurs.
où M est l'inductance mutuelle maximale possible entre 2 bobines et L1 et L2 sont les deux bobines. En général
car seule une fraction du flux propre est liée à l'autre. Cette fraction est appelée "Coefficient de liaison des flux (K)" ou "Coefficient de couplage".
Types de bobine[modifier | modifier le code]
Bobine à noyau d'air[modifier | modifier le code]
Le terme bobine à noyau d'air décrit une inductance qui n'utilise pas de noyau magnétique fait d'un matériau ferromagnétique. Ce terme fait référence aux bobines enroulées sur du plastique, de la céramique ou d'autres formes non magnétiques, ainsi qu'à celles dont les enroulements ne contiennent que de l'air. Les bobines à noyau d'air ont une inductance plus faible que les bobines à noyau ferromagnétique, mais elles sont souvent utilisées à des fréquences élevées parce qu'elles sont exemptes des pertes d'énergie appelées pertes de noyau qui se produisent dans les noyaux ferromagnétiques et qui augmentent avec la fréquence. Un effet secondaire qui peut se produire dans les bobines à air où l'enroulement n'est pas supporté de manière rigide par une forme est la "microphonie" : les vibrations mécaniques des enroulements peuvent provoquer des variations de l'inductance.
Bobine de radiofréquence[modifier | modifier le code]

À haute fréquence, en particulier aux radiofréquences (RF), les inductances présentent une résistance plus élevée et d'autres pertes. En plus de provoquer une perte de puissance, dans les circuits résonnants, cela peut réduire le facteur Q du circuit, élargissant ainsi la bande passante. Dans les bobines RF, qui sont pour la plupart des types de noyau à air, des techniques de construction spécialisées sont utilisées pour minimiser ces pertes. Les pertes sont dues aux effets suivants :
- L'effet de peau : La résistance d'un fil au courant haute fréquence est plus élevée que sa résistance au courant continu en raison de l'effet de peau. En raison des courants de Foucault induits, le courant alternatif à haute fréquence ne pénètre pas profondément dans le corps d'un conducteur mais se déplace le long de sa surface. Par exemple, à 6 MHz, la profondeur de peau d'un fil de cuivre est d'environ 25 µm, la majeure partie du courant se trouve à cette profondeur de la surface. Par conséquent, dans un fil solide, la partie intérieure du fil peut transporter peu de courant, ce qui augmente effectivement sa résistance.
- L'effet de proximité : Un autre effet similaire qui augmente également la résistance du fil à des fréquences élevées est l'effet de proximité, qui se produit dans des fils parallèles proches les uns des autres. Le champ magnétique individuel des spires adjacentes induit des courants de Foucault dans le fil de la bobine, ce qui fait que le courant dans le conducteur est concentré dans une fine bande sur le côté proche du fil adjacent. Comme l'effet de peau, cela réduit la section effective du fil conduisant le courant, ce qui augmente sa résistance.
- Les pertes diélectriques : Le champ électrique haute fréquence à proximité des conducteurs d'une bobine de réservoir peut provoquer le mouvement des molécules polaires dans les matériaux isolants voisins, dissipant ainsi de l'énergie sous forme de chaleur. Ainsi, les bobines utilisées pour les circuits accordés ne sont souvent pas enroulées sur des formes de bobines mais sont suspendues dans l'air, soutenues par des bandes étroites en plastique ou en céramique.
- La capacité parasite : La capacité entre les différentes spires de la bobine, appelée capacité parasite, ne provoque pas de pertes d'énergie mais peut modifier le comportement de la bobine. Chaque spire de la bobine est à un potentiel légèrement différent, de sorte que le champ électrique entre les spires voisines stocke la charge sur le fil, de sorte que la bobine agit comme si elle avait un condensateur en parallèle avec elle. À une fréquence suffisamment élevée, cette capacité peut entrer en résonance avec l'inductance de la bobine pour former un circuit accordé, ce qui fait que la bobine devient auto-résonante.
Pour réduire la capacité parasite et l'effet de proximité, les bobines RF à haut Q sont construites de manière à éviter d'avoir de nombreuses spires proches les unes des autres, parallèles les unes aux autres. Les enroulements des bobines RF sont souvent limités à une seule couche, et les spires sont espacées. Pour réduire la résistance due à l'effet de peau, dans les inductances de haute puissance tels que ceux utilisés dans les transmetteurs, les enroulements sont parfois constitués d'une bande ou d'un tube métallique ayant une plus grande surface, et la surface est plaquée d'argent.
Bobines en forme de panier[modifier | modifier le code]
Pour réduire l'effet de proximité et la capacité parasite, les bobines RF multicouches sont enroulées selon des motifs dans lesquels les spires successives ne sont pas parallèles mais croisées à un angle ; on parle souvent de bobines en nid d'abeille ou en panier. Ces bobines sont parfois enroulées sur un support isolant vertical muni de chevilles ou de fentes, le fil s'entrecroisant à travers les fentes.
Bobines de toile d'araignée[modifier | modifier le code]
Les bobines plates en spirale constituent une autre technique de construction présentant des avantages similaires. Celles-ci sont souvent enroulées sur un support isolant plat avec des rayons ou des fentes radiales, le fil se faufilant dans les fentes ; on les appelle des bobines en toile d'araignée. La forme présente un nombre impair de fentes, de sorte que les tours successifs de la spirale se trouvent sur des côtés opposés de la forme, ce qui augmente la séparation.
Fil de Litz[modifier | modifier le code]
Pour réduire les pertes par effet de peau, certaines bobines sont enroulées avec un type spécial de fil de radiofréquence appelé fil de Litz. Au lieu d'un seul conducteur solide, le fil de Litz est constitué d'un certain nombre de brins de fil plus petits qui transportent le courant. Contrairement au fil toronné ordinaire, les brins sont isolés les uns des autres, pour éviter que l'effet de peau ne pousse le courant vers la surface, et ils sont torsadés ou tressés ensemble. Le motif de torsion garantit que chaque brin de fil passe la même quantité de sa longueur à l'extérieur du faisceau de fils, de sorte que l'effet de peau distribue le courant de manière égale entre les brins, ce qui donne une surface de conduction transversale plus grande qu'un fil unique équivalent.
Bobine axiale[modifier | modifier le code]
Les petites inductances pour faible courant et faible puissance sont fabriquées dans des boîtiers moulés ressemblant à des résistances. Elles peuvent être à noyau ordinaire (phénolique) ou à noyau de ferrite. Un ohmmètre permet de les distinguer facilement des résistances de taille similaire en montrant la faible résistance de la bobine.

Bobine à noyau ferromagnétique[modifier | modifier le code]
Les bobines à noyau ferromagnétique ou à noyau de fer utilisent un noyau magnétique constitué d'un matériau ferromagnétique ou ferrimagnétique tel que le fer ou la ferrite pour augmenter l'inductance. Un noyau magnétique peut augmenter l'inductance d'une bobine par un facteur de plusieurs milliers, en augmentant le champ magnétique grâce à sa perméabilité magnétique plus élevée. Cependant, les propriétés magnétiques du matériau du noyau provoquent plusieurs effets secondaires qui modifient le comportement de l'inductance et nécessitent une construction spéciale :
Pertes de noyau[modifier | modifier le code]
Un courant variant dans le temps dans une inductance ferromagnétique, qui provoque un champ magnétique variant dans le temps dans son noyau, entraîne des pertes d'énergie dans le matériau du noyau qui sont dissipées sous forme de chaleur, en raison de deux processus :
- Courants de Foucault : D'après la loi d'induction de Faraday, le champ magnétique variable peut induire des boucles de courant électrique circulant dans le noyau métallique conducteur. L'énergie de ces courants est dissipée sous forme de chaleur dans la résistance du matériau du noyau. La quantité d'énergie perdue augmente avec la surface à l'intérieur de la boucle de courant.
- Hystérésis : La modification ou l'inversion du champ magnétique dans le noyau entraîne également des pertes dues au mouvement des minuscules domaines magnétiques dont il est composé. La perte d'énergie est proportionnelle à l'aire de la boucle d'hystérésis dans le graphique BH du matériau du noyau. Les matériaux à faible coercivité ont des boucles d'hystérésis étroites et donc de faibles pertes par hystérésis.
Les pertes dans le noyau sont non linéaires par rapport à la fréquence de fluctuation magnétique et à l'induction magnétique. La fréquence de fluctuation magnétique est la fréquence du courant alternatif dans le circuit électrique ; l'induction magnétique correspond au courant dans le circuit électrique. La fluctuation magnétique donne lieu à l'hystérésis, et l'induction magnétique provoque des courants de Foucault dans le noyau. Ces non-linéarités se distinguent de la non-linéarité de seuil de la saturation. La perte dans le noyau peut être modélisée approximativement avec l'équation de Steinmetz. Aux basses fréquences et sur des plages de fréquences limitées (peut-être un facteur 10), la perte dans le noyau peut être traitée comme une fonction linéaire de la fréquence avec une erreur minimale. Cependant, même dans la gamme audio, les effets non linéaires des inductances à noyau magnétique sont perceptibles et préoccupants.
Saturation[modifier | modifier le code]
Si le courant traversant une bobine à noyau magnétique est suffisamment élevé pour que le noyau sature, l'inductance diminue et le courant augmente de façon spectaculaire. Il s'agit d'un phénomène de seuil non linéaire qui entraîne une distorsion du signal. Par exemple, les signaux audio peuvent subir une distorsion d'intermodulation dans les inductances saturées. Pour éviter cela, dans les circuits linéaires, le courant traversant les inductances à noyau de fer doit être limité en dessous du niveau de saturation. Certains noyaux laminés sont dotés d'un étroit entrefer à cette fin, et les noyaux en poudre de fer ont un entrefer réparti. Cela permet des niveaux plus élevés de flux magnétique et donc des courants plus élevés à travers l'inductance avant qu'il ne sature[14].
Démagnétisation au point de Curie[modifier | modifier le code]
Si la température d'un noyau ferromagnétique ou ferrimagnétique atteint un certain niveau, les domaines magnétiques se dissocient et le matériau devient paramagnétique, c'est-à-dire qu'il n'est plus capable de supporter un flux magnétique. L'inductance diminue et le courant augmente de façon spectaculaire, comme cela se produit lors de la saturation. L'effet est réversible : Lorsque la température descend en dessous du point de Curie, le flux magnétique résultant du courant dans le circuit électrique réaligne les domaines magnétiques du noyau et son flux magnétique est restauré. Le point de Curie des matériaux ferromagnétiques (alliages de fer) est assez élevé ; le fer atteint sa température maximale à 770 °C (1043 K). Toutefois, pour certains matériaux ferrimagnétiques (composés céramiques de fer - ferrites), le point de Curie peut être proche de la température ambiante (moins de 100 °C)[15].
Bobine à noyau laminé[modifier | modifier le code]

Les bobines basse fréquence sont souvent fabriqués avec des noyaux laminés pour éviter les courants de Foucault, selon une construction similaire à celle des transformateurs. Le noyau est constitué d'empilements de fines feuilles d'acier ou de laminés orientés parallèlement au champ, avec un revêtement isolant à la surface. L'isolation empêche les courants de Foucault entre les tôles, de sorte que tout courant résiduel doit se trouver dans la section transversale des différentes lamelles, ce qui réduit la surface de la boucle et donc les pertes d'énergie. Les laminations sont fabriquées en acier au silicium à faible conductivité pour réduire davantage les pertes par courants de Foucault.
Bobine à noyau de ferrite[modifier | modifier le code]
Pour les fréquences plus élevées, les bobines sont fabriqués avec des noyaux en ferrite. La ferrite est un matériau céramique ferrimagnétique qui est non conducteur, de sorte que les courants de Foucault ne peuvent pas circuler en son sein. La formulation de la ferrite est xxFe2O4 où xx représente divers métaux. Pour les noyaux d'inductances, on utilise des ferrites douces, qui ont une faible coercivité et donc de faibles pertes par hystérésis.
Bobine à noyau toroïdal[modifier | modifier le code]

Dans une bobine enroulée sur un noyau en forme de tige droite, les lignes de champ magnétique émergeant d'une extrémité du noyau doivent traverser l'air pour réintégrer le noyau à l'autre extrémité. Cela réduit le champ, car une grande partie du trajet du champ magnétique se trouve dans l'air plutôt que dans le matériau du noyau à perméabilité plus élevée et constitue une source d'interférences électromagnétiques. Un champ magnétique et une inductance plus élevés peuvent être obtenus en formant le noyau dans un circuit magnétique fermé. Les lignes de champ magnétique forment des boucles fermées à l'intérieur du noyau sans quitter le matériau du noyau. La forme souvent utilisée est un noyau de ferrite toroïdal ou en forme de beignet. En raison de leur symétrie, les noyaux toroïdaux permettent à un minimum du flux magnétique de s'échapper à l'extérieur du noyau (appelé flux de fuite), de sorte qu'ils rayonnent moins d'interférences électromagnétiques que les autres formes. Les bobines à noyau toroïdal sont fabriquées à partir de divers matériaux, principalement la ferrite, la poudre de fer et les noyaux laminés[16].
Bobine variable[modifier | modifier le code]

Le type de bobine variable le plus courant aujourd'hui est probablement celui qui comporte un noyau magnétique en ferrite mobile, qui peut être glissé ou vissé dans ou hors de la bobine. En déplaçant le noyau plus loin dans la bobine, on augmente la perméabilité, ce qui accroît le champ magnétique et l'inductance. De nombreuses inductances utilisées dans les applications radio (généralement inférieures à 100 MHz) utilisent des noyaux ajustables afin d'accorder ces inductances à la valeur souhaitée, car les processus de fabrication présentent certaines tolérances (imprécisions). Parfois, ces noyaux pour les fréquences supérieures à 100 MHz sont fabriqués dans un matériau non magnétique hautement conducteur, tel que l'aluminium[17]. Ils diminuent l'inductance car le champ magnétique doit les contourner.
Les bobines à air peuvent utiliser des contacts coulissants ou des prises multiples pour augmenter ou diminuer le nombre de tours inclus dans le circuit, afin de modifier l'inductance. Un type très utilisé par le passé, mais aujourd'hui obsolète, comporte un contact à ressort qui peut glisser le long de la surface nue des enroulements. L'inconvénient de ce type est que le contact court-circuite généralement une ou plusieurs spires. Ces spires agissent comme un enroulement secondaire de transformateur court-circuité à une seule spire ; les courants importants qui y sont induits provoquent des pertes de puissance.
Le variomètre est un type de bobine à air à variation continue. Il s'agit de deux bobines avec le même nombre de tours connectées en série, l'une dans l'autre. La bobine intérieure est montée sur un arbre de sorte que son axe puisse être tourné par rapport à la bobine extérieure. Lorsque les axes des deux bobines sont colinéaires, avec les champs magnétiques orientés dans la même direction, les champs s'additionnent et l'inductance est maximale. Lorsque la bobine intérieure est tournée de manière que son axe fasse un angle avec la bobine extérieure, l'inductance mutuelle entre elles est plus faible et l'inductance totale est donc inférieure. Lorsque la bobine intérieure est tournée de 180° de façon que les bobines soient colinéaires avec leurs champs magnétiques opposés, les deux champs s'annulent et l'inductance est très faible. Ce type a l'avantage d'être continuellement variable sur une large gamme. Il est utilisé dans les adaptateurs d'antenne et les circuits d'adaptation pour adapter les émetteurs basse fréquence à leurs antennes.
Bobine d'arrêt[modifier | modifier le code]

Une bobine d'arrêt (choke en anglais) est une inductance conçue spécifiquement pour bloquer le courant alternatif (CA) haute fréquence dans un circuit électrique, tout en laissant passer les signaux CC ou basse fréquence. Parce que l'inductance résiste ou "étouffe" les changements de courant, ce type d'inductance est appelé une choke (étouffoir). Elle est généralement constituée d'une bobine de fil isolé enroulée sur un noyau magnétique, bien que certaines soient constituées d'une "perle" de ferrite en forme de beignet accrochée à un fil. Comme les autres inductances, les selfs résistent aux variations du courant qui les traverse de manière croissante avec la fréquence. La différence entre les selfs et les autres inductances est que les selfs ne nécessitent pas les techniques de construction à facteur Q élevé qui sont utilisées pour réduire la résistance des inductances utilisées dans les circuits accordés.
Formules usuelles pour le calcul théorique de bobines[modifier | modifier le code]
| Construction | Formule | Dimensions |
|---|---|---|
| Bobine à air |
| |
| Bobine avec noyau magnétique |
|
Code de couleurs des bobines[modifier | modifier le code]
Afin de marquer la valeur de l'inductance d'une bobine, il est parfois utilisé un code de couleur normalisé.
| Couleur | 1. Anneau | 2. Anneau | 3. Anneau multiplicateur |
4. Anneau tolérance |
|---|---|---|---|---|
| aucune | — | — | — | ±20 % |
| argent | — | — | 10−2 µH | ±10 % |
| or | — | — | 10−1 µH | ±5 % |
| noir | 0 | 0 | 100 µH | — |
| marron | 1 | 1 | 101 µH | — |
| rouge | 2 | 2 | 102 µH | — |
| orange | 3 | 3 | 103 µH | — |
| jaune | 4 | 4 | 104 µH | — |
| vert | 5 | 5 | 105 µH | — |
| bleu | 6 | 6 | 106 µH | — |
| violet | 7 | 7 | 107 µH | — |
| gris | 8 | 8 | 108 µH | — |
| blanc | 9 | 9 | 109 µH | — |
| Couleur | 1. Anneau (large) |
2. à 4. Anneau chiffre |
5. Anneau multiplicateur |
6. Anneau tolérance |
|---|---|---|---|---|
| aucune | — | — | — | ±20 % |
| argent | Début | — | — | ±10 % |
| or | — | virgule | — | ±5 % |
| noir | — | 0 | 100 µH | — |
| marron | — | 1 | 101 µH | ±1 % |
| rouge | — | 2 | 102 µH | ±2 % |
| orange | — | 3 | 103 µH | — |
| jaune | — | 4 | 104 µH | — |
| vert | — | 5 | 105 µH | ±0,5 % |
| bleu | — | 6 | 106 µH | — |
| violet | — | 7 | 107 µH | — |
| gris | — | 8 | 108 µH | — |
| blanc | — | 9 | 109 µH | — |
| Le troisième chiffre est optionnel. | ||||
Construction[modifier | modifier le code]
Une inductance est généralement constituée d'une bobine de matériau conducteur, généralement un fil de cuivre isolé, enroulé autour d'un noyau soit en plastique (pour créer une inductance à air), soit en matériau ferromagnétique (ou ferrimagnétique) ; dans ce dernier cas, on parle d'inductance à "noyau de fer". La perméabilité élevée du noyau ferromagnétique augmente le champ magnétique et le confine étroitement à la bobine, augmentant ainsi l'inductance. Les inductances basse fréquence sont construites comme des transformateurs, avec des noyaux en fer doux laminés pour éviter les courants de Foucault. Les ferrites "doux" sont largement utilisés pour les noyaux au-dessus des fréquences audio, car ils ne causent pas de grandes pertes d'énergie à haute fréquence comme les alliages de fer ordinaires. Les bobines d'inductance se présentent sous de nombreuses formes, certaines inductances ont un noyau réglable, ce qui permet de modifier l'inductance. Les bobines utilisées pour bloquer les très hautes fréquences sont parfois fabriqués en enfilant une bille de ferrite sur un fil.
Les petites inductances peuvent être gravées directement sur une carte de circuit imprimé en disposant la trace en spirale. Certaines de ces inductances planaires utilisent un noyau planaire. Les inductances de petite valeur peuvent également être construites sur des circuits intégrés en utilisant les mêmes procédés que ceux utilisés pour fabriquer les interconnexions. On utilise généralement des interconnexions en aluminium, disposées en spirale. Cependant, les petites dimensions limitent l'inductance, et il est beaucoup plus courant d'utiliser un circuit appelé gyrateur qui utilise un condensateur et des composants actifs pour se comporter de manière similaire à une inductance. Quelle que soit la conception, en raison des faibles inductances et de la faible dissipation de puissance que permettent les inducteurs sur puce, ils ne sont actuellement utilisés commercialement que pour les circuits RF haute fréquence.
Bobines blindées[modifier | modifier le code]
Les bobines d'inductance utilisées dans les systèmes de régulation de puissance, l'éclairage et d'autres systèmes nécessitant des conditions de fonctionnement à faible bruit, sont souvent partiellement ou totalement blindées[18],[19]. Dans les circuits de télécommunication utilisant des bobines d'inductance et des transformateurs répétitifs, le blindage des bobines à proximité immédiate réduit la diaphonie du circuit.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Ces applications sortent du cadre de cet article, mais elles doivent être mentionnées parce que les calculs qui leur sont nécessaires doivent prendre en compte les propriétés électriques qui sont développées plus bas.
- Voir simulateur d'inductance
- Un circuit LC, constitué d'une inductance connectée à un condensateur, agit comme un résonateur pour un courant oscillant. Les circuits accordés sont largement utilisés dans les équipements de radiofréquence tels que les émetteurs et les récepteurs radio, comme filtres passe-bande étroits pour sélectionner une fréquence unique dans un signal composite, et dans les oscillateurs électroniques pour générer des signaux sinusoïdaux.
- Les bobines d'inductance sont également employées dans les systèmes de transmission électrique, où elles servent à limiter les courants de commutation et les courants de défaut. Dans ce domaine, elles sont plus communément appelées (bobines d')inductance ou en anglais : reactors.
Références[modifier | modifier le code]
- Commission électrotechnique internationale "Vocabulaire Electrotechnique International", norme internationale ISO / CEI 60050
- Inductance, bobine d'inductance : Electropédia 151-13-25.
- La revue électrique, 1909, p. 18 [lire en ligne]
- De « self-induction » : Max Marty, Daniel Dixneuf, Delphine Garcia Gilabert, Principes d'électrotechnique – Cours et exercices corrigés, Paris, Dunod, coll. « Sciences sup », , 684 p. (ISBN 978-2-10-052633-8, présentation en ligne).
- Informations lexicographiques et étymologiques de « bobine » (sens B1) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- Roger A. Raffin, L'émission et la réception d'amateur, Paris, ETSF, 1979, p. 335-337.
- J.L. Cocquerelle, L'Électronique de commutation, Paris, Technip ; J.–P. Ferrieux, F. Forest, Alimentations à découpage — Convertisseurs à résonance, Paris, Dunod, 3e édition, 1999.
- (en) « Aircraft electrical systems », Wonderquest.com (consulté le ).
- Bogdan Grabowski, Composants de l'électronique, Dunod, 1982, p. 87.
- Voir B3.7 Régime permanent (sinusoïdal), sur le site epsic.ch, consulté le 17 janvier 2016
- (en) « An Unassuming Antenna – The Ferrite Loopstick », Radio Time Traveller, (consulté le ).
- (en) Phil Frost, « What's an appropriate core material for a loopstick antenna? », sur Amateur Radio beta, Stack Exchange, Inc., (consulté le ).
- (en) Richard Poisel, Antenna Systems and Electronic Warfare Applications, Artech House, , 280 p. (ISBN 978-1608074846, lire en ligne).
- (en) R. L. Yadava, Antenna and Wave Propagation, PHI Learning Pvt. Ltd, , 261 p. (ISBN 978-8120342910, lire en ligne).
- (en) « Inductors 101 » [PDF], vishay (consulté le )
- (en) « Ferromagnetic Curie Temperatures » (consulté le ).
- (en) « Inductor and Magnetic Product Terminology » [PDF], Vishay Dale (consulté le ).
- (en) « page with aluminum cores » [PDF] (consulté le ).
- (en) Henry W. Ott, Electromagnetic Compatibility Engineering, John Wiley and Sons, , 203 p. (ISBN 978-1118210659, lire en ligne).
- (en) Norman Violette, Electromagnetic Compatibility Handbook, Springer, , 515–516 p. (ISBN 978-9401771443, lire en ligne).
Annexes[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Calcul des bobines coaxiales
- Conception d’une bobine à air à une seule couche (calculatrice en ligne)
- Calculatrice en ligne pour déterminer l'inductance de bobines monocouches et multicouches
- Calculatrice en ligne pour déterminer l'inductance de bobines à noyau torique
- Notices dans des dictionnaires ou encyclopédies généralistes :