Moment magnétique
| Unités SI |
newton mètre par tesla (N m/T) ampère mètre carré (A m2) |
|---|---|
| Dimension | L 2·I |
| Nature | Grandeur vectorielle (pseudovecteur) extensive |
| Symbole usuel | , |
| Lien à d'autres grandeurs | = |
En physique, le moment magnétique est une grandeur vectorielle qui permet de caractériser l'intensité d'une source magnétique. Cette source peut être un courant électrique, ou bien un objet aimanté. L'aimantation est la distribution spatiale du moment magnétique.
Le moment magnétique d'un corps se manifeste par la tendance qu'a ce corps à s'aligner dans le sens d'un champ magnétique, c'est par exemple le cas de l'aiguille d'une boussole : le moment que subit l'objet est égal au produit vectoriel de son moment magnétique par le champ magnétique dans lequel il est placé. Par ailleurs, tout système possédant un moment magnétique produit également un champ magnétique autour de lui.
Le moment magnétique est souvent noté ou [a]. Il s'exprime en ampères mètres carrés (A m2).
Définition[modifier | modifier le code]
Manifestation du moment magnétique[modifier | modifier le code]

Le moment magnétique d'un corps se manifeste par la tendance qu'a ce corps à s'aligner dans le sens d'un champ magnétique. L'exemple le plus courant est celui de l'aiguille d'une boussole : laissée libre de tourner, l'aiguille s'aligne dans la direction du pôle nord, ce qui montre qu'elle subit un moment qui tend à l'aligner dans cette direction.
Le couple qui tend à ramener l'aiguille aimantée sur la direction du champ magnétique est donc proportionnel au produit vectoriel du champ magnétique et d'une quantité vectorielle extensive, caractéristique de l'aiguille, d'autant plus intense que l'aiguille est aimantée.
Par définition, le moment magnétique d'un objet est défini comme le vecteur dont le produit vectoriel par l'induction magnétique externe[b] donne le moment de force que subit l'objet. Cette relation se traduit mathématiquement par :
- .
Cette définition donne donc une méthode permettant, en théorie, de mesurer le moment magnétique d'un échantillon inconnu placé dans un champ magnétique connu. La même méthode permet symétriquement de mesurer le champ magnétique en un point, à partir d'un système comportant un moment magnétique déterminé.
Unité[modifier | modifier le code]
L'unité de moment magnétique est une unité dérivée du Système international d'unités. Comme le moment d'une force se mesure en newtons mètres (N m) et le champ magnétique en teslas (T), le moment magnétique s'exprime en newtons mètres par tesla (N m T−1). D'ordinaire on l'exprime plutôt en ampères mètres carrés (A m2), en remarquant que le tesla se confond avec le newton par ampère mètre :
- 1 N m T−1 = 1 A m2.
Lien entre moment magnétique et aimantation[modifier | modifier le code]
L'aimantation correspond à une densité volumique de moment magnétique. Elle est définie par l'équation suivante, où est le moment magnétique élémentaire, et dV le volume élémentaire :
- .
Le moment magnétique s'exprimant en ampères mètres carrés (A m2), l'intensité d'aimantation J (le module ou la valeur algébrique de l'aimantation ) se mesure en ampères par mètre (A/m).
Cette équation mène à une définition générale du moment magnétique, comme intégrale de l'aimantation sur l'ensemble du volume du corps considéré :
où est le moment magnétique total.
De ce fait, le moment magnétique et l'aimantation sont complètement analogues au moment d'un dipôle électrostatique et à la polarisation :
- , .
Cette analogie conduit à parler de dipôle magnétique par analogie avec un dipôle électrostatique.
Dipôles magnétiques[modifier | modifier le code]
Dipôles élémentaire[modifier | modifier le code]
La représentation du moment magnétique a changé au cours du temps. Avant les années 30, on le représentait par deux masses magnétiques ponctuelles. On a depuis montré qu'il n'existe pas de masses magnétiques isolées dans la nature, et que celles-ci sont donc purement fictives. On préfère donc aujourd'hui une représentation à l'aide de boucles de courant. Les deux représentations donnent des résultats similaires.
Un dipôle magnétique est la limite aussi bien d'une boucle de courant ou d'une paire de pôles magnétiques lorsque les dimensions du système tendent vers zéro tandis que son moment magnétique reste constant. Loin de la source les deux représentations sont équivalentes, mais elles divergent à proximité de la source.
Représentation à l'aide de charges magnétiques[modifier | modifier le code]
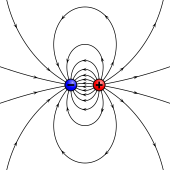
Par analogie avec l’électrostatique, les sources de moments magnétiques peuvent être représentées par des pôles (on rappelle que les monopôles magnétiques n'ont jamais été observés et que leur existence même n'est pas assurée). Considérons une barrette magnétique possédant des pôles magnétiques d’égales amplitudes mais de polarités opposées. Chaque pôle est la source d'un champ magnétique qui s’affaiblit avec la distance. Puisque les pôles magnétiques vont toujours par paires, le champ magnétique qu'ils génèrent s'annule d'autant plus que les deux pôles sont proches l'un de l'autre. Ainsi le moment magnétique est proportionnel à l’intensité p des pôles magnétiques et du vecteur ℓ qui les séparent :
Il pointe du pôle sud au pôle nord.
Représentation par une boucle de courant[modifier | modifier le code]

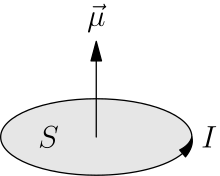
Le modèle le plus simple de moment magnétique est celui d'une boucle de courant (courant électrique circulant dans un élément de bobine par exemple). Un champ magnétique appliqué à cette boucle tendra à faire tourner la boucle de manière qu'elle soit perpendiculaire au champ magnétique, le courant tournant dans le sens direct par rapport au plan orienté par le champ magnétique. Par exemple, une bobine électrique parcourue par un courant et libre de ses mouvements s'alignera sur l'aimant qu'on approche d'elle.
On part de la définition du moment magnétique différentiel :
où est le vecteur position, et la densité de courant électrique.
De là, on peut retrouver la forme intégrale de cette équation :
- .
Dans le cas d'une particule chargée en rotation, cette expression devient :
où est le vecteur position, q la charge de la particule et son vecteur vitesse.
Dans le cas d'un fil infiniment fin comme cette boucle de courant : , d'où :
Soit :
- .
Moment magnétique d'un solénoïde[modifier | modifier le code]

On peut appliquer l'expression ci-dessus au cas d'une bobine ou d'un solénoïde. Le moment magnétique total est la somme des moments magnétiques de chaque boucle. Dans le cas d'un solénoïde constitué de N boucles de surface S :
- .
Champ magnétique produit par un dipôle[modifier | modifier le code]
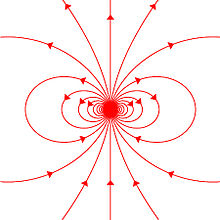
Tout système possédant un moment magnétique produit un champ magnétique autour de lui. On peut montrer que loin de la source ce champ magnétique est :
où désigne le vecteur unitaire radial (le vecteur unitaire de mêmes direction et sens que ) : .
Par suite, l'induction magnétique est :
- .
Le champ magnétique d'un dipôle idéal est représenté ci-contre.
Dipôle magnétique dans un champ magnétique[modifier | modifier le code]

À chaque dipôle magnétique est associé un moment magnétique . En présence d'un champ magnétique , ce dipôle va être soumis à un couple et une force , auxquels on peut associer une énergie potentielle Em. Ces dernières sont définies par les relations suivantes :
- ,
- ,
- .
La première équation indique que la dérivée temporelle du moment cinétique d'un dipôle magnétique est égale au couple . Or celui-ci fait intervenir le produit vectoriel du moment magnétique par le champ magnétique. Mais comme moment magnétique et moment cinétique sont proportionnels, l'équation indique que la dérivée du moment cinétique est proportionnelle au produit vectoriel du moment cinétique par le champ. Ainsi, en présence d'un champ magnétique, un dipôle magnétique va-t-il être l'objet d'un phénomène de précession, appelée dans ce contexte précession de Larmor.
Forces entre deux dipôles magnétiques[modifier | modifier le code]
La force exercée par un dipôle de moment magnétique sur un autre dipôle de moment magnétique est où est le champ magnétique créé par le moment magnétique . Le résultat de ce calcul est[1],[2] :
où est le vecteur unitaire pointant du premier dipôle vers le second, et (ou simplement ) la distance qui les sépare. On peut réécrire cette formule de la façon suivante[2] :
- .
Le moment de force subi par est :
- .
Une force et un moment de mêmes directions et de mêmes intensités mais de sens opposés s'exercent sur .
Moment magnétique et moment angulaire[modifier | modifier le code]
En mécanique classique, on peut montrer le lien existant entre le moment cinétique orbital et le moment magnétique d'une configuration possédant des charges en mouvement.
On considère une particule (un électron) de masse m suivant une trajectoire circulaire de rayon r (vecteur position ) à une vitesse . Le moment cinétique vaut alors :
- .
Le moment magnétique associé à ce courant, autrement dit au déplacement de l'électron qui génère un courant électrique , est :
- ,
où q est la charge de la particule et S la surface délimitant l'extension de son déplacement.
En combinant les deux relations ci-dessus, on obtient la relation suivante entre moments cinétique et magnétique :
- ,
ou bien :
- ,
où est appelé rapport gyromagnétique du dipôle considéré.
Exemples de moments magnétiques[modifier | modifier le code]
Les deux types de sources magnétiques[modifier | modifier le code]
Fondamentalement, il ne peut y avoir que deux types de source pour un moment magnétique : le déplacement de charge électrique, tel qu'un courant électrique, et le moment magnétique intrinsèque porté par les particules élémentaires.
Les contributions du premier type peuvent être calculées à partir d'une distribution de courant connue d'un système en utilisant la formule suivante :
- .
L’intensité du moment magnétique des particules élémentaires est une valeur fixe, souvent connue avec une grande précision.
Le moment magnétique total de tout système est la somme vectorielle de toutes les contributions quel que soit leur type. Par exemple, le moment magnétique porté par l'atome d'hydrogène-1 (le plus léger les isotopes de l'hydrogène, constitué d'un proton et d'un électron) est la somme des contributions suivantes :
- le moment intrinsèque de l’électron,
- le déplacement de l’électron autour du proton,
- le moment intrinsèque du proton.
De même le moment magnétique d'un barreau magnétique est la somme des moments magnétiques (intrinsèques et orbitaux) de chaque électron célibataire du matériau et du moment magnétique nucléaire.
Moment magnétique intrinsèque d'un électron[modifier | modifier le code]
Les électrons ainsi que la plupart des autres particules élémentaires ont un moment magnétique intrinsèque, dont l'origine est purement quantique. Il est à l'origine de la plupart des propriétés magnétiques macroscopiques des matériaux.
Le moment magnétique de spin d'un électron est
où μB est le magnéton de Bohr, le spin de l'électron, la constante de Planck réduite et gS le facteur de Landé qui vaut environ 2 dans le cas de l'électron.
On peut noter que est de sens opposé au spin (en raison de la charge négative de l'électron) : le moment magnétique est donc anti-parallèle au spin.
Moment magnétique orbital[modifier | modifier le code]
On peut transposer le lien entre le moment magnétique et le moment cinétique de la mécanique classique à la mécanique quantique. Ainsi, au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
- .
Le facteur q2m est appelé rapport gyromagnétique.
Moment magnétique d'un atome[modifier | modifier le code]
Dans un atome comportant plusieurs électrons, les moments cinétiques orbitaux et de spin de chaque électron s'ajoutent pour constituer le moment cinétique orbital total de l'atome et son moment cinétique de spin total . Le moment cinétique total est donc [3]. Le moment magnétique résultant est :
où gJ est le facteur de Landé et μB le magnéton de Bohr. La composante de ce moment suivant l'axe z est alors[4] :
où m est le nombre quantique magnétique, qui peut prendre les (2J+1) valeurs suivantes :
- .
Exemples[modifier | modifier le code]
| Particule | Symbole | Moment magnétique (J/T) |
Nombre quantique de spin (sans dimension) |
|---|---|---|---|
| électron | e− | −9,284 765 × 10−24 | ½ |
| proton | p = 1H+ = H+ | 1,410 607 × 10−26 | ½ |
| neutron | n | −9,662 365 × 10−27 | ½ |
| muon | μ− | −4,490 448 × 10−26 | ½ |
| deutéron | 2H+ = D+ | 4,330 735 × 10−27 | 1 |
| triton | 3H+ = T+ | 1,504 610 × 10−26 | ½ |
| hélion | 3He2+ | −1,074 618 × 10−26 | ½ |
| particule α | 4He2+ | 0 | 0 |
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- En anglais le moment magnétique est plutôt noté ou . Attention, en anglais désigne souvent l'aimantation, que l'on note plus souvent en français.
- Par « induction magnétique externe » on entend l'induction magnétique générée par tous les aimants ou circuits, à l'exception de l'objet aimanté lui-même.
Références[modifier | modifier le code]
- Edward P. Furlani, Permanent Magnet and Electromechanical Devices : Materials, Analysis, and Applications, Academic Press, , 518 p. (ISBN 0-12-269951-3, lire en ligne), p. 140.
- K.W. Yung, P.B. Landecker et D.D. Villani, « An Analytic Solution for the Force between Two Magnetic Dipoles », Magnetic and Electrical Separation, (lire en ligne [PDF], consulté le ).
- RJD Tilley, Understanding Solids, John Wiley and Sons, (ISBN 0-470-85275-5, lire en ligne), p. 368.
- (en) Paul Allen Tipler, Ralph A. Llewellyn, Modern Physics, Macmillan, , 4e éd. (ISBN 0-7167-4345-0, lire en ligne), p. 310
- « Search results matching ' magnetic moment '... », CODATA internationally recommended values of the Fundamental Physical Constants, National Institute of Standards and Technology (consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Marc Knecht ; The anomalous magnetic moments of the electron and the muon, séminaire Poincaré (Paris, ), publié dans : Bertrand Duplantier et Vincent Rivasseau (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), (ISBN 3-7643-0579-7). Texte complet disponible au format PostScript.
Articles connexes[modifier | modifier le code]
- Champ magnétique
- Constante fondamentale
- Dipôle magnétique d'une sphère
- Électrodynamique quantique
- Expérience de Rabi
- Magnétisme
- Magnéton nucléaire
- Magnétostatique
- Mécanique quantique
- Moment cinétique orbital
- Moment cinétique quantique
- Moment magnétique anomal
- Moment magnétique de l'électron
- Moment magnétique du neutron
- Moment magnétique du proton
- Monopôle magnétique
- Spin
- Théorie quantique des champs
- aimant moléculaire






























![{\displaystyle {\vec {H}}({\vec {r}})={\frac {1}{4\pi }}\left[{\frac {3\,({\vec {\mu }}\cdot {\vec {r}})\,{\vec {r}}}{|{\vec {r}}|^{5}}}-{\frac {\vec {\mu }}{|{\vec {r}}|^{3}}}\right]={\frac {1}{4\pi |{\vec {r}}|^{3}}}[3\,({\vec {\mu }}\cdot {\hat {r}})\,{\hat {r}}-{\vec {\mu }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f9abf87cdfafe3468247130757280df24e0919)


![{\displaystyle {\vec {B}}({\vec {r}})=\mu _{0}\,{\vec {H}}({\vec {r}})={\frac {\mu _{0}}{4\pi |{\vec {r}}|^{3}}}[3\,({\vec {\mu }}\cdot {\hat {r}})\,{\hat {r}}-{\vec {\mu }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72259f7ebfc30b4eb384dd2a5e7fbf37441b90f9)







![{\displaystyle {\vec {F}}({\vec {r}},{\vec {\mu }}_{1},{\vec {\mu }}_{2})={\frac {3\mu _{0}}{4\pi |{\vec {r}}|^{4}}}[({\vec {\mu }}_{1}\cdot {\hat {r}})\,{\vec {\mu }}_{2}+({\vec {\mu }}_{2}\cdot {\hat {r}})\,{\vec {\mu }}_{1}+({\vec {\mu }}_{1}\cdot {\vec {\mu }}_{2})\,{\hat {r}}-5({\vec {\mu }}_{1}\cdot {\hat {r}})({\vec {\mu }}_{2}\cdot {\hat {r}})\,{\hat {r}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83f59bc20033d6af2e5730ef0af3c16eaaa4e8e4)


![{\displaystyle {\vec {F}}={\frac {3\mu _{0}}{4\pi |{\vec {r}}|^{4}}}[({\hat {r}}\wedge {\vec {\mu }}_{1})\wedge {\vec {\mu }}_{2}+({\hat {r}}\wedge {\vec {\mu }}_{2})\wedge {\vec {\mu }}_{1}-2({\vec {\mu }}_{1}\cdot {\vec {\mu }}_{2})\,{\hat {r}}+5({\hat {r}}\wedge {\vec {\mu }}_{1})\cdot ({\hat {r}}\wedge {\vec {\mu }}_{2})\,{\hat {r}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2695f4b34cbc79736e9d0c2b35646175fbea7898)



















