Circuit LC

Cet article est une ébauche concernant l’électronique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Consultez la liste des tâches à accomplir en page de discussion.

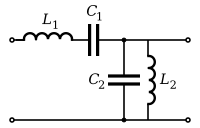
Un circuit LC est un circuit électrique contenant une bobine (L) et un condensateur (Capacité). C'est ainsi qu'on obtient le phénomène de résonance électrique.

Ce type de circuit est utilisé dans les filtres, les tuners et les mélangeurs de fréquences. Par conséquent, son utilisation est répandue dans les transmissions sans fil en radiodiffusion, autant pour l'émission que la réception.

Résonance électrique[modifier | modifier le code]

Fonctionnement[modifier | modifier le code]

Le phénomène de résonance électrique se produit dans un circuit électrique à une fréquence de résonance donnée où les parties imaginaires des impédance ou admittance des éléments de circuit s'annulent. Dans certains circuits, la résonance électrique a lieu lorsque l'impédance entre l'entrée et la sortie du circuit est près de zéro et la fonction de transfert est près de l'unité. Les circuits résonants comportent des retentissements et peuvent générer de plus hautes tensions et courants que ceux qu'ils reçoivent, ce qui les rend utiles pour la transmission sans fil.

Dans un circuit composé de condensateurs et de bobines, le champ magnétique dans une bobine induit un courant électrique dans les enroulements de cette bobine pour charger un condensateur. Lorsqu'il se décharge, le condensateur produit un courant électrique qui renforce le champ magnétique dans la bobine. Ce processus est répété continuellement, de façon comparable au processus de balancement d'un pendule mécanique. Dans certains cas, la résonance a lieu lorsque les réactances de bobine et de condensateur sont de magnitudes égales, de sorte que l'énergie électrique oscille entre le champ magnétique de la bobine et le champ électrique du condensateur.

Fréquence de résonance[modifier | modifier le code]

La pulsation propre ou de résonance d'un circuit LC (en radians par seconde) est :

\omega _{0}={1 \over {\sqrt {LC}}}

Ce qui nous donne la fréquence propre ou de résonance d'un circuit LC en hertz :

f_{0}={\omega _{0} \over 2\pi }={1 \over {2\pi {\sqrt {LC}}}}

Impédance[modifier | modifier le code]

LC série[modifier | modifier le code]

L'impédance d'un circuit série est donnée par la somme des impédances de chacun de ses constituants. Soit dans notre cas :

Z=Z_{L}+Z_{C}\,

Avec $Z_{L}=j\omega L\,$ l'impédance de la bobine et $Z_{C}={\frac {1}{j\omega C}}\,$ l'impédance du condensateur.

Z=j\omega L+{\frac {1}{j\omega C}}

Ce qui nous donne une fois réduit au même dénominateur :

Z={\frac {(\omega ^{2}LC-1)j}{\omega C}}

On remarquera que l'impédance est nulle à la pulsation de résonance $\omega _{0}={\sqrt {1 \over LC}}$ mais pas ailleurs.

Le circuit se comporte donc comme un filtre passe-bande ou comme un filtre coupe-bande, selon la manière dont il est disposé dans le réseau considéré.

LC parallèle[modifier | modifier le code]

L'impédance du circuit est donnée par la formule :

Z={\frac {Z_{L}Z_{C}}{Z_{L}+Z_{C}}}

Après substitution de $Z_{L}\,$ et $Z_{C}\,$ par leurs formules littérales, on obtient :

Z={\frac {\frac {L}{C}}{\frac {(1-\omega ^{2}LC)}{j\omega C}}}

Qui se simplifie en :

Z={\frac {jL\omega }{1-\omega ^{2}LC}}

On remarque que $\lim _{\omega ^{2}LC\to 1}Z=\infty$ alors que l'impédance est finie pour les autres fréquences.

Le circuit LC parallèle présente donc une impédance infinie à la fréquence de résonance. Selon la façon dont on le dispose dans un réseau, il pourra agir comme un filtre passe bande ou comme un filtre coupe bande.

Sélectivité[modifier | modifier le code]

Les circuits LC sont souvent utilisés comme filtres. Si un circuit LC est utilisé comme filtre passe bande, on définit généralement sa bande passante à - 3dB autour de sa fréquence de résonance. On aura alors le « coefficient de surtension » Q égal au rapport entre la fréquence de résonance et la bande passante:

Q={\frac {f_{0}}{BP}}

Plus le coefficient de surtension est élevé, plus le circuit est « sélectif ».

Dans toutes les utilisations pratiques, le circuit LC est en fait associé à des résistances : résistance de l'inductance, résistances connectées sur l'entrée et sur la sortie du filtre, etc. Il s'agit donc en fait d'un circuit RLC. Par des transformations convenables, on peut traduire l'effet de toutes ces résistances de deux manières :

soit par une seule résistance équivalente R_s en série dans le circuit ;
soit par une seule résistance équivalente R_p en parallèle sur le circuit.

Un Q élevé correspond à une résistance série R_s faible, ou à une résistance parallèle R_p grande.

On peut calculer Q en fonction des résistances ci-dessus :

Q={\frac {Z}{R_{s}}}={\frac {R_{p}}{Z}}

Où Z est le module des impédances de la bobine ou du condensateur (qui sont les mêmes à la fréquence de résonance).

Coefficient de surtension à vide Qo et coefficient de surtension en charge Qc :

Un circuit LC réel n'a jamais un coefficient de surtension infini, car il y aura toujours des pertes par les résistances ohmiques dans l'inductance, par le rayonnement, par les pertes diélectriques dans le condensateur, etc. On appelle Q à vide, noté Qo, ce coefficient de surtension du circuit seul.

Lorsque le circuit LC est utilisé dans un montage, pour adapter ou pour filtrer des signaux, on lui rajoute toujours des résistances, souvent en parallèle. Le coefficient de surtension est alors plus faible. On appelle Q en charge, noté Qc, le coefficient de surtension du circuit ainsi « chargé ».

Quand le circuit LC est utilisé en filtre ou en adaptateur, on minimisera les pertes de transmission sur la fréquence de résonance, en rendant maximum le rapport Qo /Qc.

Applications[modifier | modifier le code]

Références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Electrical resonance » (voir la liste des auteurs).

Voir aussi[modifier | modifier le code]

Portail de l’électricité et de l’électronique

v · m Électricité
Généralité	Glossaire Histoire Économie Circuit électrique intensité du courant tension électrique
Mesure	Ampèremètre pince ampèremétrique Multimètre Ohmmètre Voltmètre Wattmètre
Composant	Antenne Accumulateur Batterie Bobine Condensateur Conducteur Connectique Diode Machine électrique Pile Résistance Rhéostat Shunt Supercondensateur Thermistance
Notions théoriques	Admittance Capacité Conductance Conductivité Courant Impédance Inductance Réactance Résistivité Susceptance Tension Vitesse de l'électricité
Automatique Électrochimie Électromagnétisme Électronique Électrotechnique Robotique Traitement du signal

v · m Électromagnétisme
Électrostatique	Champ électrique Charge électrique Loi de Coulomb Potentiel électrique Pression électrostatique
Magnétostatique	Champ magnétique Moment magnétique Aimantation Loi de Biot et Savart
Électrocinétique	Ampère Champ électromagnétique Courant de déplacement Courant électrique Courants de Foucault Équations de Jefimenko Équations de Maxwell Force électromotrice Force de Lorentz Induction électromagnétique Loi de Lenz-Faraday Potentiels de Liénard-Wiechert Rayonnement électromagnétique
Magnétisme	Bobine Circuit magnétique Domaine de Weiss Inversion du champ magnétique terrestre Loi de Curie Loi de Curie-Weiss Perméabilité magnétique Susceptibilité magnétique Comportements magnétiques Altermagnétisme Antiferromagnétisme Diamagnétisme Ferrimagnétisme Ferromagnétisme Hélimagnétisme Paramagnétisme Superparamagnétisme Verre de spin
Automatique Électricité Électrochimie Électronique Électrotechnique Robotique Traitement du signal