Théorème de Minkowski

En mathématiques, le théorème de Minkowski concerne les réseaux de l'espace euclidien ℝ^d. Étant donné un tel réseau Λ, il garantit l'existence, dans tout convexe symétrique de volume suffisant, d'un vecteur non nul de Λ. Hermann Minkowski a découvert ce théorème en 1891 et l'a publié en 1896, dans son livre fondateur de la géométrie des nombres. Ce résultat est en particulier utilisé en théorie algébrique des nombres.

Le convexe est symétrique par rapport à l'origine O (le point bleu). Il ne contient aucun autre point de ℤ³ que O ; la contraposée du théorème affirme que son volume est inférieur à 2³ = 8.

Énoncés

Première formulation —  Soit d un entier strictement positif et C un convexe de ℝ^d, symétrique par rapport à l'origine O.

• Si le volume de C est strictement supérieur à 2^d, alors C contient au moins deux points à coordonnées entières et différents de l'origine.
• Si C est compact et de volume égal à 2^d, on a la même conclusion.

Ce résultat concernant le réseau ℤ^d est équivalent (par simple changement de variables) à son homologue pour un réseau quelconque Λ :

Reformulation en termes de réseau —  Soit d un entier strictement positif, Λ un réseau de ℝ^d de covolume V et C un convexe O-symétrique.

• Si le volume de C est strictement supérieur à 2^dV, alors C contient au moins deux vecteurs non nuls du réseau.
• Si C est compact et de volume égal à 2^dV, on a la même conclusion.

Équivalence entre les deux énoncés

Exemple de réseau dans ℝ³.

Un réseau de ℝ^d est une partie de la forme $\Lambda =\mathbb {Z} b_{1}\oplus \dots \oplus \mathbb {Z} b_{d}$ où $B=(b_{1},\dots ,b_{d})$ est une base de ℝ^d. Le réseau est donc composé des points dont les coordonnées dans la base B sont entières. On obtient un maillage régulier de l'espace, à l'image de la figure de droite. Les points du réseau sont représentés par les petites billes.

Un domaine fondamental de Λ, dépendant de la base B, est constitué des points de ℝ^d dont les coordonnées dans la base B sont dans l'intervalle [0, 1[. Il est illustré sur la figure de droite en rouge. Un domaine fondamental est toujours un parallélépipède.

Le covolume de Λ est le volume d'un domaine fondamental. Il est donc égal à la valeur absolue du déterminant de B dans la base canonique (cette définition ne dépend pas du choix de B, car un changement de base du réseau est nécessairement de déterminant ±1).

Le domaine fondamental du réseau ℤ^d associé à la base canonique est [0, 1[^d donc le covolume de ℤ^d est 1. Le premier énoncé est ainsi un cas particulier du second. Mais inversement, par changement de variables, le second se déduit du premier, auquel nous nous consacrerons donc désormais.

Remarques

La valeur 2^d est bien la plus petite possible pour que le théorème soit vrai.

• La valeur 2^d est bien la plus petite possible. En effet, le convexe ]–1, 1[^d, de volume 2^d, ne contient que l'origine comme point à coordonnées entières. Cette situation est illustrée sur la figure de droite, le point bleu représentant l'origine.
• Un convexe de volume fini non nul étant borné, un convexe fermé de volume 2^d est compact. Il revient donc au même, dans le cas où le volume de C est égal à 2^d, de supposer simplement que C est fermé.
• Tout convexe O-symétrique de volume > 2^d contient un convexe O-symétrique compact de volume 2^d. Le premier point du théorème est donc un cas particulier du second. Réciproquement, le second peut se déduire du premier, par la même méthode que dans la démonstration du théorème de Blichfeldt.
• Un convexe compact de ℝ^d est O-symétrique et de volume non nul si et seulement si sa jauge est une norme. Il est alors égal à la boule unité fermée pour cette norme.

Démonstration

Si C_1/2 rencontre un translaté par un vecteur β de ℤ^d, la différence β = x – (–y) des deux points de C_1/2 correspondants appartient à ℤ^d.

Il existe plusieurs démonstrations du théorème. Celle présentée ici dissocie l'hypothèse sur le volume de C — qui permettra d'appliquer le théorème de Blichfeldt — de celle sur ses deux autres propriétés (convexité et symétrie), utilisée dans le lemme suivant.

Lemme. — Soit C_1/2 = 1/2C l'image de C par l'homothétie de rapport 1/2. Si C_1/2 rencontre un translaté β + C_1/2, alors C contient β.

Supposons que x = β – y où x et –y sont deux points de C_1/2 (c'est ce qui est illustré sur la figure de droite). Alors, 2x et –2y appartiennent à C donc (comme C est O-symétrique) 2x et 2y aussi et (par convexité de C) leur milieu x + y = β aussi (et –β aussi), ce qui achève la preuve du lemme.

D'après le théorème de Blichfeldt, puisque C_1/2 est de volume strictement supérieur à 1, ou compact et de volume 1, il contient deux points distincts dont la différence β est à coordonnées entières. Autrement dit : il existe un vecteur non nul β de ℤ^d tel que C_1/2 rencontre le translaté β + C_1/2. D'après le lemme, C contient alors β, ce qui termine la démonstration du théorème.

Interprétation géométrique

Le quotient de ℝ^d par ℤ^d est un tore de dimension d.

Illustration de la preuve dans le plan : les deux points X et Y dans C_1/2 (en jaune) fournissent Z = X – Y, point de ℤ^d dans le convexe C (en vert).

Il existe une manière d'interpréter cette démonstration en termes de groupe topologique. L'espace ℝ^d peut être vu comme un groupe topologique dont ℤ^d est un sous-groupe discret. Quotienter ℝ^d par ℤ^d revient à identifier chaque élément de ℝ^d avec un élément de [0, 1[^d. En dimension 2, cela revient à coller les points de [0, 1]² (la maille du réseau) dont la première coordonnée est égale à 1 avec ceux dont la première coordonnée est égale à 0, et agir de même avec la deuxième coordonnée. On obtient un tore de dimension d, illustré pour d = 2 par la figure de gauche. Chaque point de ℝ^d possède un voisinage tel que l'application canonique de ℝ^d dans le tore se restreigne en un difféomorphisme entre ce voisinage et son image. Ces difféomorphismes permettent de définir une mesure sur le tore, telle que toute partie mesurable du domaine fondamental soit mesurable sur le tore et de même mesure. La mesure du tore est donc 1.

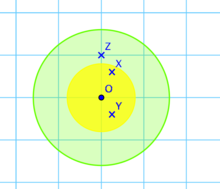
Cette mesure est l'outil de la démonstration directe. On suppose que le convexe C, illustré en vert dans l'exemple de droite, est de mesure strictement supérieure à 2^d. Son homothétique C_1/2, illustré en jaune, est de mesure strictement supérieure à 1. La restriction à C_1/2 de l'application canonique de ℝ^d dans le tore ne peut être injective car la mesure de l'image serait supérieure à celle du tore tout entier. Il existe donc deux éléments de C_1/2, X et Y (les points x et –y du lemme), ayant même image par cette application.

• 
  Le dessin montre comment différents morceaux de C_1/2 (disque jaune) sont « recollés » dans le tore.
• 
  La partie du convexe C_1/2 qui est envoyée injectivement dans le tore apparaît en jaune

Lors du recollement expliqué plus haut, des morceaux de C_1/2 se trouvent superposés, les points ainsi superposés ont la même image. En revenant à la figure originelle, à l'inverse, la zone d'injectivité correspond à ce qui apparaît encore en jaune dans la figure de droite. Le point X – Y = x + y de C est à coordonnées entières non toutes nulles car X et Y sont deux représentants différents d'une même classe.

Applications

Ce théorème est utilisé pour démontrer deux résultats importants en théorie algébrique des nombres : le théorème des unités de Dirichlet et la finitude du groupe des classes d'idéaux d'un corps de nombres (par exemple un corps quadratique). Dans le second, le réseau considéré est le groupe additif de l'anneau des entiers algébriques du corps.

Une autre application est une démonstration du théorème des quatre carrés de Lagrange.

Réciproque partielle

On peut montrer avec des hypothèses supplémentaires une réciproque partielle au théorème de Minkowski:

Réciproque partielle —  Soit d un entier strictement positif et P une partie étoilée de ℝ^d, symétrique par rapport à l'origine O, et de volume V < 2ζ(d). Alors il existe un réseau de covolume 1 dont aucun point autre que l'origine n'appartient à P.

Généralisations

Soient à nouveau, dans ℝ^d, un réseau Λ de covolume V et un convexe C égal à la boule unité fermée pour une certaine norme (voir supra). Notons λ₁ ≤ … ≤ λ_d les minima successifs de Λ relativement à C. En particulier, λ₁ est la plus petite norme d'un vecteur non nul de Λ, donc le théorème de Minkowski équivaut (par homogénéité) à : λ₁^d vol(C) ≤ 2^dV.

• Cette majoration est renforcée par celle du second théorème de Minkowski :λ₁…λ_d vol(C) ≤ 2^dV.
• Cassels et Lagarias attribuent à van der Corput une autre généralisation du (premier) théorème de Minkowski :Si vol(C) ≥ k2^d pour un certain entier k, alors C contient au moins 2k vecteurs non nuls de Λ.

Voir aussi

Articles connexes

• Borne de MinkowskiBorne de Minkowski
• Corps convexe (en)
• Théorème d'approximation de Dirichlet

Liens externes

• Phong Q. Nguyen, La géométrie des nombres : de Gauss aux codes secrets, École normale supérieure, université Denis Diderot
• (en) « Proof of Minkowski's theorem », sur PlanetMath

Bibliographie

Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]