Théorème de Minkowski
En mathématiques, le théorème de Minkowski concerne les réseaux de l'espace euclidien ℝd. Étant donné un tel réseau Λ, il garantit l'existence, dans tout convexe symétrique de volume suffisant, d'un vecteur non nul de Λ. Hermann Minkowski a découvert ce théorème en 1891[1] et l'a publié en 1896, dans son livre fondateur de la géométrie des nombres[2]. Ce résultat est en particulier utilisé en théorie algébrique des nombres.

Énoncés[modifier | modifier le code]
Première formulation — Soit d un entier strictement positif et C un convexe de ℝd, symétrique par rapport à l'origine O.
- Si le volume de C est strictement supérieur à 2d, alors C contient au moins deux points à coordonnées entières et différents de l'origine.
- Si C est compact et de volume égal à 2d, on a la même conclusion.
Ce résultat concernant le réseau ℤd est équivalent (par simple changement de variables) à son homologue pour un réseau quelconque Λ :
Reformulation en termes de réseau — Soit d un entier strictement positif, Λ un réseau de ℝd de covolume V et C un convexe O-symétrique.
- Si le volume de C est strictement supérieur à 2dV, alors C contient au moins deux vecteurs non nuls du réseau.
- Si C est compact et de volume égal à 2dV, on a la même conclusion.
Équivalence entre les deux énoncés[modifier | modifier le code]

Un réseau de ℝd est une partie de la forme où est une base de ℝd. Le réseau est donc composé des points dont les coordonnées dans la base B sont entières. On obtient un maillage régulier de l'espace, à l'image de la figure de droite. Les points du réseau sont représentés par les petites billes.
Un domaine fondamental de Λ, dépendant de la base B, est constitué des points de ℝd dont les coordonnées dans la base B sont dans l'intervalle [0, 1[. Il est illustré sur la figure de droite en rouge. Un domaine fondamental est toujours un parallélépipède.
Le covolume de Λ est le volume d'un domaine fondamental. Il est donc égal à la valeur absolue du déterminant de B dans la base canonique (cette définition ne dépend pas du choix de B, car un changement de base du réseau est nécessairement de déterminant ±1).
Le domaine fondamental du réseau ℤd associé à la base canonique est [0, 1[d donc le covolume de ℤd est 1. Le premier énoncé est ainsi un cas particulier du second. Mais inversement, par changement de variables, le second se déduit du premier, auquel nous nous consacrerons donc désormais.
Remarques[modifier | modifier le code]

- La valeur 2d est bien la plus petite possible. En effet, le convexe ]–1, 1[d, de volume 2d, ne contient que l'origine comme point à coordonnées entières. Cette situation est illustrée sur la figure de droite, le point bleu représentant l'origine.
- Un convexe de volume fini non nul étant borné[3], un convexe fermé de volume 2d est compact. Il revient donc au même, dans le cas où le volume de C est égal à 2d, de supposer simplement que C est fermé.
- Tout convexe O-symétrique de volume > 2d contient un convexe O-symétrique compact de volume 2d. Le premier point du théorème est donc un cas particulier du second. Réciproquement, le second peut se déduire du premier, par la même méthode que dans la démonstration du théorème de Blichfeldt.
- Un convexe compact de ℝd est O-symétrique et de volume non nul si et seulement si sa jauge est une norme. Il est alors égal à la boule unité fermée pour cette norme[4],[5].
Démonstration[modifier | modifier le code]

Il existe plusieurs démonstrations du théorème[6],[7],[8]. Celle présentée ici dissocie l'hypothèse sur le volume de C — qui permettra d'appliquer le théorème de Blichfeldt — de celle sur ses deux autres propriétés (convexité et symétrie), utilisée dans le lemme suivant.
Lemme. — Soit C1/2 = 12C l'image de C par l'homothétie de rapport 1/2. Si C1/2 rencontre un translaté β + C1/2, alors C contient β.
Supposons que x = β – y où x et –y sont deux points de C1/2 (c'est ce qui est illustré sur la figure de droite). Alors, 2x et –2y appartiennent à C donc (comme C est O-symétrique) 2x et 2y aussi et (par convexité de C) leur milieu x + y = β aussi (et –β aussi), ce qui achève la preuve du lemme.
D'après le théorème de Blichfeldt, puisque C1/2 est de volume strictement supérieur à 1, ou compact et de volume 1, il contient deux points distincts dont la différence β est à coordonnées entières. Autrement dit : il existe un vecteur non nul β de ℤd tel que C1/2 rencontre le translaté β + C1/2. D'après le lemme, C contient alors β, ce qui termine la démonstration du théorème[9].
Interprétation géométrique[modifier | modifier le code]

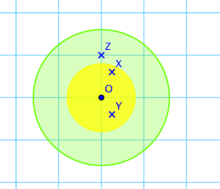
Il existe une manière d'interpréter cette démonstration en termes de groupe topologique. L'espace ℝd peut être vu comme un groupe topologique dont ℤd est un sous-groupe discret. Quotienter ℝd par ℤd revient à identifier chaque élément de ℝd avec un élément de [0, 1[d. En dimension 2, cela revient à coller les points de [0, 1]2 (la maille du réseau) dont la première coordonnée est égale à 1 avec ceux dont la première coordonnée est égale à 0, et agir de même avec la deuxième coordonnée. On obtient un tore de dimension d, illustré pour d = 2 par la figure de gauche. Chaque point de ℝd possède un voisinage tel que l'application canonique de ℝd dans le tore se restreigne en un difféomorphisme entre ce voisinage et son image. Ces difféomorphismes permettent de définir une mesure sur le tore, telle que toute partie mesurable du domaine fondamental soit mesurable sur le tore et de même mesure. La mesure du tore est donc 1.
Cette mesure est l'outil de la démonstration directe. On suppose que le convexe C, illustré en vert dans l'exemple de droite, est de mesure strictement supérieure à 2d. Son homothétique C1/2, illustré en jaune, est de mesure strictement supérieure à 1. La restriction à C1/2 de l'application canonique de ℝd dans le tore ne peut être injective car la mesure de l'image serait supérieure à celle du tore tout entier. Il existe donc deux éléments de C1/2, X et Y (les points x et –y du lemme), ayant même image par cette application.
-
Le dessin montre comment différents morceaux de C1/2 (disque jaune) sont « recollés » dans le tore.
-
La partie du convexe C1/2 qui est envoyée injectivement dans le tore apparaît en jaune
Lors du recollement expliqué plus haut, des morceaux de C1/2 se trouvent superposés, les points ainsi superposés ont la même image. En revenant à la figure originelle, à l'inverse, la zone d'injectivité correspond à ce qui apparaît encore en jaune dans la figure de droite. Le point X – Y = x + y de C est à coordonnées entières non toutes nulles car X et Y sont deux représentants différents d'une même classe.
Applications[modifier | modifier le code]
Ce théorème est utilisé pour démontrer deux résultats importants en théorie algébrique des nombres : le théorème des unités de Dirichlet et la finitude du groupe des classes d'idéaux d'un corps de nombres (par exemple un corps quadratique). Dans le second, le réseau considéré est le groupe additif de l'anneau des entiers algébriques du corps[10].
Une autre application est une démonstration du théorème des quatre carrés de Lagrange.
Réciproque partielle[modifier | modifier le code]
On peut montrer avec des hypothèses supplémentaires une réciproque partielle au théorème de Minkowski[11]:
Réciproque partielle — Soit d un entier strictement positif et P une partie étoilée de ℝd, symétrique par rapport à l'origine O, et de volume V < 2ζ(d). Alors il existe un réseau de covolume 1 dont aucun point autre que l'origine n'appartient à P.
Généralisations[modifier | modifier le code]
Soient à nouveau, dans ℝd, un réseau Λ de covolume V et un convexe C égal à la boule unité fermée pour une certaine norme (voir supra). Notons λ1 ≤ … ≤ λd les minima successifs de Λ relativement à C. En particulier, λ1 est la plus petite norme d'un vecteur non nul de Λ, donc le théorème de Minkowski équivaut (par homogénéité)[12] à : λ1d vol(C) ≤ 2dV.
- Cette majoration est renforcée par celle du second théorème de Minkowski :λ1…λd vol(C) ≤ 2dV.
- Cassels et Lagarias attribuent à van der Corput[13] une autre généralisation du (premier) théorème de Minkowski :Si vol(C) ≥ k2d pour un certain entier k, alors C contient au moins 2k vecteurs non nuls de Λ.
Notes et références[modifier | modifier le code]
- (de) H. Minkowski, « Über Geometrie der Zahlen », dans Verhandlungen der 64. Naturforscher- und Arzteversammlung zu Halle, , p. 13 ; reproduit dans (de) David Hilbert (éd.), Gesammelte Abhandlungen von Hermann Minkowski, vol. 1, (lire en ligne), p. 264-265.
- (de) Hermann Minkowski, Geometrie der Zahlen, Teubner, Leipzig, 1896, § 30.
- (en) John W. S. Cassels, An Introduction to the Geometry of Numbers, Berlin, Göttingen, Heidelberg, Springer, coll. « Grund. math. Wiss. » (no 99), (1re éd. 1959), 344 p. (lire en ligne), p. 109.
- (en) Jeffrey C. Lagarias, chap. 19 « Point Lattices », dans R. L. Graham, M. Grötschel et L. Lovász, Handbook of Combinatorics, vol. I, Elsevier, (lire en ligne), p. 919-966.
- Cassels 1971, chap. IV (« Distance-Functions »), § IV.1-IV.3.1, p. 103-111.
- (de) Ott-Heinrich Keller (de), « Geometrie der Zahlen », dans Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, vol. I.2, Heft 11, Teil 3, 27, Leipzig, Teubner, , 84 p. (lire en ligne).
- (en) Jesús A. De Loera, Raymond Hemmecke et Matthias Köppe, Algebraic and Geometric Ideas in the Theory of Discrete Optimization, SIAM, (lire en ligne), p. 41-42.
- Pour un compte-rendu de la démonstration originale de Minkowski, voir (en) Pascale Gruber et Cornelis Gerrit Lekkerkerker, Geometry of Numbers, North-Holland, , 2e éd. (1re éd. 1969, 510 p.)), 731 p. (lire en ligne), p. 40-41.
- Cassels 1971, p. 71.
- Pour des exemples, voir le § « Groupe des classes » de l'article sur les idéaux de l'anneau des entiers d'un corps quadratique.
- G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition], chapitre 24 (« Géométrie des nombres »), section 24.10.
- Lagarias 1995, p. 929.
- (de) J. van der Corput, « Verallgemeinerung einer Mordellschen Beweismethode in der Geometrie der Zahlen », Acta Arithmetica, vol. 1, no 1, , p. 62-66 (lire en ligne) (Lagarias 1995, p. 930 et 965) ou (de) J. van der Corput, « Verallgemeinerung einer Mordellschen Beweismethode in der Geometrie der Zahlen, Zweite Mitteilung », Acta Arithmetica, vol. 2, no 1, , p. 145-146 (lire en ligne) (Cassels 1971, p. 71 et 336).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Phong Q. Nguyen, La géométrie des nombres : de Gauss aux codes secrets, École normale supérieure, université Denis Diderot
- (en) « Proof of Minkowski's theorem », sur PlanetMath
Bibliographie[modifier | modifier le code]
Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]




