Sextant

Un sextant est un instrument de navigation à réflexion servant à mesurer la distance angulaire entre deux points aussi bien verticalement qu'horizontalement. Il est utilisé principalement pour faire le point hors de vue de terre en relevant la hauteur angulaire d’un astre au-dessus de l’horizon (voir l’article : navigation astronomique). Un usage courant du sextant est de relever la hauteur angulaire du soleil à midi, ce qui permet de déterminer la latitude du point de l'observation à l'aide d'une table de déclinaison du soleil. On peut aussi l'utiliser en navigation côtière pour calculer la distance à un amer, ou l'angle horizontal entre deux points remarquables. Le sextant est toujours utilisé dans l’aéronautique, la marine, les raids terrestres, etc., bien que son usage se restreigne en raison du développement des systèmes de positionnement par satellites, il n'en demeure pas moins un moyen fiable dont le navigateur devra savoir faire bon usage (sa présence demeure obligatoire à bord des navires marchands)[1].
Histoire[modifier | modifier le code]

Le sextant moderne fut inventé dans les années 1730 par deux personnes indépendamment l’une de l’autre : John Hadley (1682-1744), un mathématicien et astronome britannique, et Thomas Godfrey (1704-1749), un inventeur américain britannique.
La spécificité du sextant par rapport à l’astrolabe est que les deux directions dont on veut mesurer l’angle sont observées en même temps, ce qui rend la mesure à peu près indépendante des mouvements du navire. Le sextant se tient à hauteur des yeux, alors que l’astrolabe nécessite un point de suspension d’autant plus élevé que l’on vise un astre de site élevé.
Principe[modifier | modifier le code]

Le sextant permet de mesurer des angles jusqu'à 120° bien que le limbe ne fasse qu'un sixième de cercle (ce qui lui vaut son nom). C'est grâce à la double réflexion du jeu de miroir qu'est réalisée cette action. Le milieu entourant le sextant sera supposé transparent, homogène et isotrope (c'est-à-dire partout le même sans dévier les rayons lumineux). En appliquant les lois de Snell-Descartes, les indices de réfractions étant les mêmes (l'air est identique autour du sextant), l'angle incident et l'angle réfléchi sont donc égaux.
Soit A le grand miroir, AM’ son plan tangent est perpendiculaire à la normale au grand miroir ; B le petit miroir, BM’ son plan tangent est perpendiculaire à la normale au petit miroir.
Dans le triangle quelconque ABM’, la somme des angles est égale à 180°
Dans le triangle quelconque ABC, la somme des angles est égale à 180°
Afin de pouvoir effectuer des lectures directes sur le limbe, les degrés qui y sont gravés sont en fait des demi-degrés. Le tambour et la vis micrométrique permettront une précision de mesure en rapport avec les calculs nautiques.
Précision des mesures et réglage[modifier | modifier le code]

La lecture d’un sextant bien réglé permet une précision de 0,2′ d’arc. En théorie, un observateur pourrait donc déterminer sa position avec une précision de 0,2 mille marin (puisqu'un mille correspond à 1′ d’arc de grand cercle), soit environ 370 mètres. Dans la pratique, les navigateurs obtiennent une précision de l’ordre de 2 à 5 milles marins (mouvements du navire, houle, horizon plus ou moins net, imprécisions de l’heure ou de l’estime entre les visées successives du même astre ou d’astres différents).
Les erreurs instrumentales du sextant sont l’excentricité et la collimation.
- L’excentricité est une donnée propre du sextant à la construction et ne peut être corrigée. Elle est fonction de la hauteur mesurée et est inscrite sur le certificat dans la boîte du sextant. Sa valeur est fonction de l'angle mesuré.
- La collimation peut être réglée et il y a lieu de la vérifier avant chaque observation en superposant l’image directe d’un astre et son image réfléchie et inversement, la collimation étant égale à la moyenne de ces deux mesures.
Si la collimation dépasse 3′, il faut vérifier et rectifier :
- l’axe optique (vieux sextants), qui doit être parallèle au plan du limbe, en comparant les visées d’une mire à 30 m. par la lunette et par des cavaliers posés sur le limbe. On agit ensuite sur les vis de réglage du collier porte-lunette ;
- le grand miroir, qui doit être, en comparant la visée directe d’un cavalier avec la visée réfléchie par le grand miroir d’un second cavalier. On agit ensuite sur la vis de réglage du grand miroir ;
- le petit miroir, qui doit être perpendiculaire au plan du limbe et parallèle au grand miroir, en visant un point éloigné ou l’horizon : les deux images doivent être confondues et le rester en inclinant le sextant. On agit sur les vis de réglage du petit miroir.
Les erreurs et corrections non instrumentales, qui viennent entacher la précision de la mesure sont :
+ Les corrections liées au protocole de mesure
- La dépression : l'œil de l'observateur n'étant pas au niveau du sol, son horizon visible est plus éloigné que l'horizon vrai.
- Le demi-diamètre : les mesures sont supposées faites en prenant le centre de l'astre sur l'horizon, ce qui en pratique n'est pas possible pour les corps célestes proches et entraine une autre correction à apporter.
- La réfraction : le rayon lumineux venant de l'espace et entrant dans l'atmosphère terrestre change de milieu de propagation, par là-même son trajet s'en trouve dévié (on ne voit pas l'astre « où il est », comme la paille dans le verre d'eau)
- Le parallaxe : l'observateur est supposé au centre de la terre pendant les mesures, ce qui n'est bien sûr pas le cas, et entraine de ce fait une autre correction.
Tous ces facteurs correctifs ne sont pas « parfaits », par exemple les indices de réfraction sont donnés dans les tables en fonction de la température et de la pression atmosphérique (mesurées à bord) et ne seront que partiellement représentatifs des conditions sur le trajet du rayon lumineux.
+ Les erreurs de l'observateur
- erreur d'angle : en fonction de la netteté de l'horizon, de la clarté du ciel, de la qualité du sextant, de l'habileté de l'observateur.
- erreur de temps : le navigateur doit coordonner sa mesure d'angle avec une prise du temps, la parfaite synchronisation des mesures est indispensable, le chronomètre doit être à l'heure à la seconde près (ou sa correction de marche connue)
- erreur sur la position estimée au moment de la mesure : voir l'article droite de hauteur.
Mesure de la hauteur d'un astre au sextant[modifier | modifier le code]
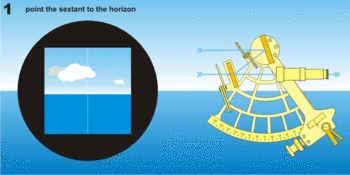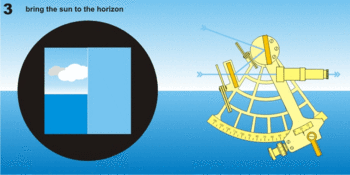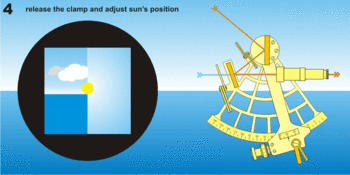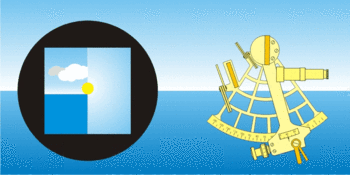
Avant, et pendant les mesures de jour, on utilisera les deux jeux de filtres associés aux miroirs. Celui du petit miroir permettant d'éviter d'être ébloui par l'horizon, celui du grand miroir protégeant l'œil de la lumière du soleil. L’observation consiste à « faire descendre » l’image réfléchie de l’astre sur l’horizon et la faire tangenter l’horizon (d’où le mouvement de balancier de la main qui tient le sextant). S’il s’agit du soleil ou de la lune, on fait tangenter son bord inférieur ou supérieur. Pour les étoiles et les planètes, il est conseillé de « monter l’horizon » au voisinage de l’astre en retournant le sextant, puis d’observer normalement.
La hauteur mesurée au sextant doit être corrigée des erreurs instrumentales et d’un certain nombre de paramètres propres à la hauteur de l’observateur au-dessus de l’eau, à la réfraction astronomique et à l’astre visé.
La hauteur vraie est déduite de la hauteur mesurée par la formule
- avec :
- , l’excentricité du sextant, invariable 'défaut de construction';
- , la collimation du sextant ;
- , la dépression de l’horizon, fonction de la hauteur de l’œil de l’observateur, donné par les éphémérides ;
- , la réfraction astronomique, liée à l'atmosphère terrestre ;
- , la parallaxe (négligeable pour les étoiles et les planètes), due au fait que l'observateur se suppose au centre de la terre ;
- , le demi-diamètre (apparent) de la lune ou du soleil, affecté du signe + si on a visé le bord inférieur, du signe - si on a visé le bord supérieur.
Pour le soleil, les éphémérides donnent la valeur journalière de ainsi que la somme ; étant le demi-diamètre moyen et on applique une deuxième correction : pour le bord inférieur et pour le bord supérieur.
Pour la lune on applique une formule analogue avec des valeurs données par les éphémérides.
Pour les étoiles et planètes : est négligeable ; est négligeable, sauf pour Mars et Vénus. La somme est fournie par les éphémérides ainsi que la valeur de pour Mars et Vénus.
Autres usages[modifier | modifier le code]
- Distance d'un amer
On mesure au sextant la hauteur angulaire d’un amer dont on connaît la hauteur. Il convient toutefois d’être prudent :
- l’édifice doit être complètement visible : il ne doit pas avoir les pieds dans l’eau et ne pas être en partie derrière l’horizon ;
- il ne faut pas confondre la hauteur de l’édifice avec l’élévation du foyer d’un phare ou d’un feu, qui seule est mentionnée sur les cartes marines et comptée depuis le niveau des hautes mers de vives-eaux moyennes (coefficient 95).
La distance exprimée en milles marins est : avec la hauteur de l’édifice en mètres et la hauteur instrumentale en minutes.
- Angles horizontaux
En utilisant le sextant dans le plan horizontal, il est possible de mesurer l’angle entre deux objets. Cette méthode permet de faire un point par arcs capables ; voir l’article : Navigation côtière.
- Voyages spatiaux
Les premiers vols spatiaux, notamment ceux du programme Apollo, ont utilisé des appareils de mesure fondés sur le même principe que les sextants pour se repérer dans l'espace[2].
Production[modifier | modifier le code]
En 2022, il est produit en Allemagne, aux États-Unis, en France par l'entreprise CPI établie à Saint-Vincent-du-Boulay en 1997 (1 700 euros et deux mois de délai) et en Russie[3].
Notes et références[modifier | modifier le code]
- SOLAS Chapitre V, Régulation 19
- (en) Paul E. Ceruzzi (National Air and Space Museum), « Sextant, Apollo Guidance and Navigation System », Navigation Museum, Institute of Navigation.
- https://www.leparisien.fr/eure-27/dans-leure-pierre-lorho-est-le-dernier-fabricant-francais-de-sextant-06-09-2022-AZHXUT63BRDXXJJWGVY2ZSCGQU.php
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Navigation astronomique
- Histoire de la navigation astronomique
- Quadrant de navigation
- Astrolabe nautique
- Bâton de Jacob
- Quartier de Davis
- Anneau équinoxial
- Octant
- Astrodôme
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Média:livre Instruments nautiques Pierre Deseck. Publié en 1976 par les Éditions Toulon à Oostende .
- (en) The American pratical Navigator - chapitre16 :Instruments for celestial navigation[PDF], (Bowditch, NIMA 2002) : un cours complet sur le sextant
- Fiche de synthèse sur le sextant[PDF], (Charbonnel, 2005) : présentation des différents réglages et de l’utilisation d’un sextant (rectification, collimation, mesure de hauteur)
- Voir un schéma détaillé du Sextant
- Voir un schéma de principe du Sextant animé par une applet Cabrijava
- Voir des exemples de Sextants
- Site de vulgarisation
























