« Échelle de Möbius » : différence entre les versions

Cette page est un portail de qualité. Cliquez pour plus d’informations.
Un article de Wikipédia, l'encyclopédie libre.
Modification suivante →
Contenu supprimé Contenu ajouté
VisuelWikicode
MathsPoetry (discuter | contributions)
49 468 modifications
création à partir de la page anglaise
(Aucune différence)

Version du 8 février 2013 à 10:10

Cet article est en cours de réécriture ou de restructuration importante (indiquez la date de pose grâce au paramètre date).

Un utilisateur prévoit de modifier cet article pendant plusieurs jours. Vous êtes invité(e) à en discuter en page de discussion et à participer à son amélioration de préférence en concertation pour des modifications de fond.

Two views of the Möbius ladder M16. For an animation showing the transformation between the two views, see this file.

In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges (called "rungs") connecting opposite pairs of vertices in the cycle. It is so-named because (with the exception of M6 = K3,3) Mn has exactly n/2 4-cycles (McSorley 1998) which link together by their shared edges to form a topological Möbius strip. Möbius ladders were named and first studied by Guy and Harary (1967).

Properties

Every Möbius ladder is a nonplanar apex graph. Möbius ladders have crossing number one, and can be embedded without crossings on a torus or projective plane. Thus, they are examples of toroidal graphs. Li (2005) explores embeddings of these graphs onto higher genus surfaces.

Möbius ladders are vertex-transitive but (again with the exception of M6) not edge-transitive: each edge from the cycle from which the ladder is formed belongs to a single 4-cycle, while each rung belongs to two such cycles.

When n ≡ 2 (mod 4), Mn is bipartite. When n ≡ 0 (mod 4), by Brooks' theorem Mn has chromatic number 3. De Mier and Noy (2005) show that the Möbius ladders are uniquely determined by their chromatic polynomials.

The Möbius ladder M8 has 392 spanning trees; it and M6 have the most spanning trees among all cubic graphs with the same number of vertices (Jakobson and Rivin 1999; Valdes 1991). However, the 10-vertex cubic graph with the most spanning trees is the Petersen graph, which is not a Möbius ladder.

Graph minors

The Wagner graph M8

Möbius ladders play an important role in the theory of graph minors. The earliest result of this type is a 1937 theorem of Klaus Wagner that graphs with no K5 minor can be formed by using clique-sum operations to combine planar graphs and the Möbius ladder M8; for this reason M8 is called the Wagner graph.

Gubser (1996) defines an almost-planar graph to be a nonplanar graph for which every nontrivial minor is planar; he shows that 3-connected almost-planar graphs are Möbius ladders or members of a small number of other families, and that other almost-planar graphs can be formed from these by a sequence of simple operations.

Maharry (2001) shows that almost all graphs that do not have a cube minor can be derived by a sequence of simple operations from Möbius ladders.

Chemistry and physics

Walba et al. (1982) first synthesized molecular structures in the form of a Möbius ladder, and since then this structure has been of interest in chemistry and chemical stereography (Simon 1993), especially in view of the ladder-like form of DNA molecules. With this application in mind, Modèle:Harvs studies the mathematical symmetries of embeddings of Möbius ladders in R3.

Möbius ladders have also been used as the shape of a superconducting ring in experiments to study the effects of conductor topology on electron interactions (Mila et al. 1998; Deng et al. 2002).

Combinatorial optimization

Möbius ladders have also been used in computer science, as part of integer programming approaches to problems of set packing and linear ordering. Certain configurations within these problems can be used to define facets of the polytope describing a linear programming relaxation of the problem; these facets are called Möbius ladder constraints (Bolotashvili et al. 1999; Borndörfer and Weismantel 2000; Grötschel et al. 1985a, 1985b; Newman and Vempala 2004).

See also

References

  • Bolotashvili, G.; Kovalev, M.; Girlich, E., « New facets of the linear ordering polytope », SIAM Journal on Discrete Mathematics, vol. 12, no 3,‎ , p. 326–336 (DOI 10.1137/S0895480196300145)
  • Borndörfer, Ralf; Weismantel, Robert, « Set packing relaxations of some integer programs », Mathematical Programming, Series A, vol. 88, no 3,‎ , p. 425–450 (DOI 10.1007/PL00011381)
  • Deng Wen-Ji; Xu Ji-Huan; Liu Ping, « Period halving of persistent currents in mesoscopic Möbius ladders », Chinese Physics Letters, vol. 19, no 7,‎ , p. 988–991 (DOI 10.1088/0256-307X/19/7/333, arXiv cond-mat/0209421)
  • Erica Flapan, « Symmetries of Möbius ladders », Mathematische Annalen, vol. 283, no 2,‎ , p. 271–283 (DOI 10.1007/BF01446435)
  • Grötschel, M.; Jünger, M.; Reinelt, G., « On the maximum acyclic subgraph polytope », Mathematical Programming, vol. 33,‎ , p. 28–42 (DOI 10.1007/BF01582009)
  • Grötschel, M.; Jünger, M.; Reinelt, G., « Facets of the linear ordering polytope », Mathematical Programming, vol. 33,‎ , p. 43–60 (DOI 10.1007/BF01582010)
  • Gubser, Bradley S., « A characterization of almost-planar graphs », Combin. Probab. Comput., vol. 5, no 3,‎ , p. 227–245 (DOI 10.1017/S0963548300002005)
  • Guy, Richard K.; Harary, Frank, « On the Möbius ladders », Canadian Mathematical Bulletin, vol. 10,‎ , p. 493–496
  • Jakobson, Dmitry; Rivin, Igor, « On some extremal problems in graph theory », {{Article}} : paramètre « périodique » manquant,‎ (arXiv math.CO/9907050)
  • Li, De-ming, « Genus distributions of Möbius ladders », Northeastern Mathematics Journal, vol. 21, no 1,‎ , p. 70–80
  • Maharry, John, « A characterization of graphs with no cube minor », Journal of Combinatorial Theory, Series B, vol. 80, no 2,‎ , p. 179–201 (DOI 10.1006/jctb.2000.1968)
  • McSorley, John P., « Counting structures in the Möbius ladder », Discrete Mathematics, vol. 184, nos 1–3,‎ , p. 137–164 (DOI 10.1016/S0012-365X(97)00086-1)
  • de Mier, Anna; Noy, Marc, « On graphs determined by their Tutte polynomials », Graphs Combin., vol. 20, no 1,‎ , p. 105–119 (DOI 10.1007/s00373-003-0534-z)
  • Mila, Frédéric; Stafford, C. A.; Capponi, Sylvain, « Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons », Physical Review B, vol. 57, no 3,‎ , p. 1457–1460 (DOI 10.1103/PhysRevB.57.1457, lire en ligne)
  • Newman, Alantha; Vempala, Santosh « Fences are futile: on relaxations for the linear ordering problem » () (lire en ligne)
    — « (ibid.) », dans Integer programming and combinatorial optimization (Utrecht, 2001), Berlin, Lecture Notes in Computer Science, no. 2081, Springer-Verlag, p. 333–347
  • Simon, Jonathan « Knots and chemistry » ()
    — « (ibid.) », dans New scientific applications of geometry and topology (Baltimore, MD, 1992), Providence, RI, Proc. Sympos. Appl. Math., no. 45, American Mathematical Society, p. 97–130
  • Valdes, L., « Extremal properties of spanning trees in cubic graphs », Congr. Numer., vol. 85,‎ , p. 143–160
  • Wagner, K., « Über eine Eigenschaft der ebenen Komplexe », Mathematische Annalen, vol. 114,‎ , p. 570–590 (DOI 10.1007/BF01594196)
  • Walba, D.; Richards, R.; Haltiwanger, R.C., « Total synthesis of the first molecular Möbius strip », Journal of the American Chemical Society, vol. 104, no 11,‎ , p. 3219–3221 (DOI 10.1021/ja00375a051)

External links


Portail des
Mathématiques
Introduction

Les mathématiques, du grec máthēma (μάθημα) signifiant « connaissance, science », constituent un domaine de savoir, de recherche et d'enseignement, fondé sur le raisonnement logique. Elles portent sur les nombres, les formes, les opérations et d'autres notions qui permettent entre autres de modéliser l'évolution dans le temps, les procédures, notamment en informatique, et même le hasard.

L'histoire des mathématiques s'appuie sur une pratique du calcul probablement plus ancienne que l'écriture, mais ne commence en tant que telle qu'avec l'établissement des premiers théorèmes numériques ou géométriques.

Les mathématiques irriguent toutes les disciplines scientifiques et sont utilisées en économie ou dans les innovations technologiques, mais elles ont aussi des relations avec la philosophie, les arts plastiques, la musique et même les jeux et la littérature.

Lumière sur…
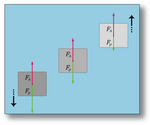
Trois solides de densités différentes peuvent subir une poussée d'Archimède inférieure, égale ou supérieure à leur poids.
Trois solides de densités différentes peuvent subir une poussée d'Archimède inférieure, égale ou supérieure à leur poids.

La poussée d'Archimède est une force, telle que définie par la mécanique newtonienne, qui agit sur tous les corps solides plongés dans un fluide. Pour pouvoir l'appréhender plus facilement, elle est généralement décrite par une phrase qui stipule "Tout corps plongé dans un fluide reçoit de la part de celui-ci une poussée verticale, dirigée de bas en haut, égale au poids du volume de fluide déplacé.".

Cette force provient de l'augmentation de la pression du fluide avec la profondeur (effet de la gravité sur le fluide, voir l'article hydrostatique) : la pression étant plus forte sur la partie inférieure d'un objet immergé que sur sa partie supérieure, il en résulte une poussée globalement verticale orientée vers le haut. C'est à partir de cette poussée qu'on définit la flottabilité d'un corps. Cette force permet notamment aux bateaux de pouvoir flotter sur l'eau.

Une légende court sur les circonstances de sa découverte: Archimède aurait eu l'intuition de cette relation alors qu'il était dans son bain en voyant son corps subir cette force, il aurait alors crié le célèbre « Eurêka ! » (j'ai trouvé !).

Articles distingués

Mathématiques générales : Nombre d'or • Énigme des trois maisons • Racine carrée de deux • Système électoral • Théorème du minimax de von Neumann

Histoire des mathématiques : Algèbre nouvelle • Isabella Bachmakova • Jean de Beaugrand • Michel Coignet • Leonhard Euler • Marin Ghetaldi • Albert Girard • Pierre Hérigone • Bernt Michael Holmboe • Hypatie • Émile Lemoine • Kenneth O. May • Emmy Noether • Srinivasa Ramanujan • Marian Rejewski • Adrien Romain • Hugo Steinhaus • Thalès • François Viète • Théorie des équations (histoire des sciences)

Algèbre : Équation • Théorème fondamental de l'algèbre • Corps fini • Représentations d'un groupe fini

Analyse : Tribu (mathématiques) • Théorème de Cauchy-Lipschitz

Arithmétique : Arithmétique modulaire • Nombre irrationnel

Géométrie : Géométrie euclidienne • Périmètre • Théorème de Pythagore • Théorème de Thalès • Loi des cosinus • Vecteur • Coordonnées polaires • Variété (géométrie) • Géométrie différentielle des surfaces • Espace à quatre dimensions

Probabilités et statistique : Analyse des données • Écart type • Exploration de données • Loi binomiale • Loi de probabilité • Loi normale • Variables indépendantes et identiquement distribuées

Topologie : Théorème du point fixe de Brouwer

Algorithmique : Algorithme de colonies de fourmis

Informatique théorique : Problème du sac à dos • Hypercube (graphe) • Théorème de Robertson-Seymour

Image du jour

Application de la transformation du photomaton à la représentation de la Joconde.

Vous souhaitez participer ?
Participer
Participer

Venez visiter le projet mathématiques ou mathématiques élémentaires pour savoir comment procéder ou prendre connaissance des recommandations.

Venez aussi visiter le Projet de la géométrie si vous êtes spécialement intéressé par la géométrie.

Venez aussi visiter le Projet des Probabilités et statistique si vous êtes spécialement intéressé par les probabilités et statistique.


Remarque : Les articles concernant ce portail peuvent y être liés grâce au bandeau {{Portail mathématiques}} à placer en fin de page. Les articles concernant le domaine « mathématiques élémentaires » sont repérés par la palette de navigation {{Palette Mathématiques élémentaires}} en fin de page. Un autre bandeau à fond jaune, {{Ébauche|mathématiques}}, placé en tête d'article, marque ceux qui ne sont encore qu'à l'état d'ébauche.

En dehors de Wikipedia

Wikiversity

Logo de la Wikiversity
Logo de la Wikiversity

Wikiquote

Wikibooks logo
Wikibooks logo

Citations

Branches des mathématiques




v · m
Discussions

Ce portail a été reconnu comme « portail de qualité » le 20 septembre 2005 (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion ainsi que le vote l’ayant promu.

Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Échelle_de_Möbius&oldid=88526344 ».