Problème du sac à dos

En algorithmique, le problème du sac à dos, parfois noté (KP) (de l'anglais Knapsack Problem)[1] est un problème d'optimisation combinatoire. Ce problème classique en informatique et en mathématiques modélise une situation analogue au remplissage d'un sac à dos. Il consiste à trouver la combinaison d'éléments la plus précieuse à inclure dans un sac à dos, étant donné un ensemble d'éléments décrits par leurs poids et valeurs.
L'objectif du problème du sac à dos est de sélectionner des objets à mettre dans le sac à dos de façon à maximiser la somme des valeurs des objets pris, sous la contrainte que le poids total des objets pris ne dépasse pas la capacité du sac à dos. Ce problème est NP-complet. Ainsi, il est difficile à résoudre, en particulier pour les grands ensembles d'objets.
Pour résoudre le problème du sac à dos, il existe plusieurs algorithmes et approches différentes, notamment la programmation dynamique, les algorithmes gloutons et la programmation en nombres entiers. Ces algorithmes peuvent être appliqués à un large éventail de problèmes réels, tels que préparer une valise pour un voyage, allouer des ressources dans une chaîne d'approvisionnement et optimiser la gestion des stocks.
Histoire[modifier | modifier le code]
Dans la recherche[modifier | modifier le code]
Le problème du sac à dos est l'un des 21 problèmes NP-complets de Richard Karp, exposés dans son article de 1972. Il est intensivement étudié depuis le milieu du XXe siècle et on trouve des références dès 1897, dans un article de George Ballard Mathews (en)[2]. La formulation du problème est fort simple, mais sa résolution est plus complexe. Les algorithmes existants peuvent résoudre des instances pratiques de taille importante. Cependant, la structure singulière du problème, et le fait qu'il soit présent en tant que sous-problème d'autres problèmes plus généraux, en font un sujet de choix pour la recherche.
Complexité et cryptographie[modifier | modifier le code]
Ce problème est à la base du premier algorithme de chiffrement asymétrique (ou à « clé publique ») présenté par Martin Hellman, Ralph Merkle et Whitfield Diffie à l'université Stanford en 1976[3]. Toutefois, même si l'idée est due au problème du sac à dos (dont l'algorithme porte le nom) , il est considéré comme le premier véritable algorithme de chiffrement asymétrique juste avant RSA publié l'année suivante.
La version NP-difficile de ce problème a été utilisée dans des primitives et des protocoles de cryptographie, tels que le cryptosystème de Merkle-Hellman[4] ou le cryptosystème de Chor-Rivest. Leur avantage par rapport aux cryptosystèmes asymétriques fondés sur la difficulté de factoriser est leur rapidité de chiffrement et de déchiffrement. Cependant, l'algorithme de Hellman, Merkle et Diffie est sujet aux « portes dérobées » algorithmiques, ce qui implique qu'il est « cassé », c'est-à-dire cryptanalysé[5]. Le problème du sac à dos est un exemple classique de méprise en ce qui concerne les liens entre la NP-complétude et la cryptographie. Une version revue de l'algorithme, avec une itération du problème du sac à dos, a alors été présentée, pour être sitôt cassée[6]. Les algorithmes de chiffrement asymétrique fondés sur le sac à dos ont tous été cassés à ce jour[4], le dernier en date étant celui de Chor-Rivest[7].
Autres domaines concernés[modifier | modifier le code]
On l'utilise aussi pour modéliser les situations suivantes, quelquefois en tant que sous-problème :
- dans des systèmes d'aide à la gestion de portefeuille : pour équilibrer sélectivité et diversification dans le but de trouver le meilleur rapport entre rendement et risque pour un capital placé sur plusieurs actifs financiers (actions...) ;
- dans le chargement de bateau ou d'avion : tous les bagages à destination doivent être amenés, sans être en surcharge ; ou l’optimisation d’un navire de charge (cargo polyvalent ou porte-conteneurs) en fonction de plusieurs critères : poids, volume, destination, marchandises spécifiques (dangereuses ou frigorifiques), importance des clients…etc ;
- dans la découpe de matériaux : pour minimiser les chutes lors de la découpe de sections de longueurs diverses dans des barres en fer, de rouleaux de papier ou de textile etc.[8]
Une autre raison de s'intéresser à ce problème est son apparition dans certaines utilisations de méthodes de génération de colonnes (ainsi pour le problème de « bin packing »).
Anecdotiquement et justifiant ainsi le nom du problème, un randonneur y est confronté au moment de préparer son périple : le sac à dos a une capacité limitée et il faut donc trancher entre prendre, par exemple, deux boîtes de conserve et une gourde de cinquante centilitres ou une seule boîte de conserve et une gourde d'un litre.
Énoncé mathématique[modifier | modifier le code]
Les données du problème peuvent être exprimées en termes mathématiques. Les objets sont numérotés par l'indice i variant de 1 à n. Les nombres wi et pi représentent respectivement le poids et la valeur de l'objet numéro i. La capacité du sac sera notée W.
Il existe de multiples façons de remplir le sac à dos. Pour décrire l'une d'elles il faut indiquer pour chaque élément s'il est pris ou non. On peut utiliser un codage binaire : l'état du i-ème élément vaudra xi = 1 si l'élément est mis dans le sac, ou xi = 0 s'il est laissé de côté. Une façon de remplir le sac est donc complètement décrite par un vecteur, appelé vecteur contenu, ou simplement contenu : ; et le poids associé, ainsi que la valeur associée, à ce remplissage, peuvent alors être exprimés comme fonction du vecteur contenu.
Pour un contenu X donné, la valeur totale contenue dans le sac est naturellement :
De même, la somme des poids des objets choisis est :
Le problème peut alors être reformulé comme la recherche d'un vecteur contenu (les composantes valant 0 ou 1), réalisant le maximum de la fonction valeur totale z(X), sous la contrainte : (1) C'est-à-dire que la somme des poids des objets choisis ne dépasse pas la capacité du sac à dos.
En général, on ajoute les contraintes suivantes afin d'éviter les cas singuliers :
- : on ne peut pas mettre tous les objets ;
- : aucun objet n'est plus lourd que ce que le sac peut porter ;
- : tout objet a une valeur et apporte un gain ;
- : tout objet a un certain poids et consomme des ressources.
Terminologie :
- z(X) est appelée fonction objectif ;
- tout vecteur X vérifiant la contrainte (1) est dit réalisable ;
- si la valeur de z(X) est maximale, alors X est dit optimal.
NP-complétude[modifier | modifier le code]
Le problème du sac à dos peut être représenté sous une forme décisionnelle en remplaçant la maximisation par la question suivante : un nombre k étant donné, existe-t-il une valeur des pour laquelle , avec respect de la contrainte ? Sous sa forme décisionnelle, lorsque les nombres sont représentés en notation binaire, le problème est NP-complet, ce qui signifie que l'on ne connaît pas de méthode générale pour construire une solution optimale, à part l'examen systématique de toutes les solutions envisageables. Le problème d'optimisation est NP-difficile, sa résolution est au moins aussi difficile que celle du problème de décision, et il n'existe pas d'algorithme polynomial connu (polynomial en le nombre de chiffres pour décrire une instance) qui, étant donné une solution, peut dire si elle est optimale (ce qui reviendrait à dire qu'il n'existe pas de solution avec un k plus grand, donc à résoudre le problème de décision NP-complet).
Il y a un lien entre la version « décision » et la version « optimisation » du problème dans la mesure où s'il existe un algorithme polynomial qui résout la version « décision », alors on peut trouver la valeur maximale pour le problème d'optimisation de manière polynomiale en effectuant de la dichotomie pour trouver k entre 1 et et en appelant l'algorithme polynomial qui résout la version « décision » (attention, si on parcourt toutes les valeurs de k de 1 à on obtiendrait un algorithme exponentiel en la taille de l'instance). D'autre part, si un algorithme trouve la valeur optimale du problème d'optimisation en un temps polynomial, alors le problème de décision peut être résolu en temps polynomial en comparant la valeur de la solution sortie par cet algorithme avec la valeur de k. Ainsi, les deux versions du problème sont de difficulté similaire.
Procédé d'exploration systématique[modifier | modifier le code]
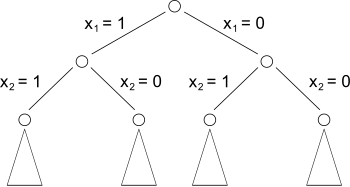
Cet examen systématique peut être réalisé à l'aide d'un arbre d'exploration binaire tel celui représenté ci-contre (les triangles représentent des sous-arbres).
L'arbre se décrit en descendant depuis le sommet jusqu'au bas des triangles (les feuilles de l'arbre). Chaque case correspond à un unique parcours possible. En suivant les indications portées le long des arêtes de l'arbre, à chaque parcours correspond une suite de valeurs pour formant un vecteur contenu. Il est alors possible de reporter dans chaque case la valeur totale et le poids total du contenu correspondant. Il ne reste plus qu'à éliminer les cases qui ne satisfont pas la contrainte, et à choisir parmi celles qui restent celle (ou une de celles) qui donne la plus grande valeur à la fonction objectif.
À chaque fois qu'un objet est ajouté à la liste des objets disponibles, un niveau s'ajoute à l'arbre d'exploration binaire, et le nombre de cases est multiplié par 2. L'exploration de l'arbre et le remplissage des cases ont donc un coût qui croît exponentiellement avec le nombre n d'objets.
Preuve de la NP-complétude[modifier | modifier le code]
Cette preuve de NP-complétude a été présentée par Michail G. Lagoudakis[9] reprenant un article de Richard Karp et un article de J.E. Savage.
Résolution approchée[modifier | modifier le code]
Comme pour la plupart des problèmes NP-complets, il peut être intéressant de trouver des solutions réalisables mais non optimales. De préférence avec une garantie sur l'écart entre la valeur de la solution trouvée et la valeur de la solution optimale.
On appelle efficacité d'un objet le rapport de sa valeur sur son poids. Plus la valeur de l'objet est importante par rapport à ce qu'il consomme, plus l'objet est efficace.
Algorithme glouton[modifier | modifier le code]
L'algorithme le plus simple est un algorithme glouton. L'idée est d'ajouter en priorité les objets les plus efficaces, jusqu'à saturation du sac :
trier les objets par ordre décroissant d'efficacité
w_conso := 0
pour i de 1 à n
si w[i] + w_conso ≤ W alors
x[i] := 1
w_conso := w_conso + w[i]
sinon
x[i] := 0
fin si
fin pour

Analyse de l'algorithme glouton[modifier | modifier le code]
On notera z* la valeur des solutions optimales.
La solution X retournée par l'algorithme glouton peut être d'aussi mauvaise qualité que possible. Considérons par exemple que nous n'ayons que deux objets à placer dans le sac. Le premier a un profit de 2 et un poids de 1, le deuxième a un profit et un poids tous deux égaux à W. Le premier objet est le plus efficace, il sera choisi en premier et empêchera la prise du second, donnant ainsi une solution de valeur 2 alors que la solution optimale vaut W. Il existe donc des valeurs du problème pour lesquelles le rapport entre la solution trouvée et la solution optimale est aussi proche de zéro que possible.
Il existe d'autres algorithmes d'approximation pour le problème de sac à dos permettant d'avoir une solution garantie à une distance k ou à un rapport ε de la qualité de solution optimale. C’est-à-dire que la solution X trouvée est telle que ou . La complexité en temps de ces algorithmes est, en général, fonction de l'inverse de la qualité attendue ; par exemple ou . Les temps d'exécution peuvent être très importants.
Métaheuristiques[modifier | modifier le code]
Les méthodes métaheuristiques comme les algorithmes génétiques ou les optimisations basées sur des algorithmes de colonies de fourmis permettent d'obtenir une approximation raisonnable tout en évitant de monopoliser trop de ressources.
Algorithme génétique[modifier | modifier le code]

Les algorithmes génétiques sont souvent utilisés dans les problèmes d'optimisation difficiles comme celui du sac à dos. Ils sont relativement faciles à mettre en œuvre et permettent d'obtenir rapidement une solution satisfaisante même si la taille du problème est importante.
On génère une population d'individus dont les chromosomes symbolisent une solution du problème. La représentation d'un individu est binaire puisque chaque objet sera soit retenu, soit écarté du sac. Le nombre de bits dans le génome de chaque individu correspond au nombre d'objets disponibles.
L'optimisation suit les principes habituels de l'algorithme génétique. Les individus sont évalués puis les meilleurs sont retenus pour la reproduction. Selon l'évolution retenue, les opérateurs de reproduction peuvent être plus ou moins complexes (cross-over), des mutations peuvent également intervenir (remplacement d'un 0 par 1 ou l'inverse). On peut également décider de copier le meilleur individu pour la génération suivante (élitisme). Après un certain nombre de générations, la population tend vers un optimum, voire la solution exacte.
Algorithmes basés sur les colonies de fourmis[modifier | modifier le code]

Ce concept a été utilisé pour résoudre le problème du sac à dos multidimensionnel où plusieurs contraintes doivent être satisfaites. Les premiers algorithmes s'appuyaient sur l'idée de l'algorithme glouton : les fourmis sélectionnaient progressivement les objets les plus intéressants. Cette sélection peut varier mais se base toujours sur des traces de phéromones déposées par les fourmis et qui conditionnent les choix ultérieurs. Parmi les solutions proposées, on peut citer le dépôt de phéromone sur les meilleurs objets, le dépôt sur des paires d'objets insérés l'un après l'autre dans la solution ou encore l'ajout de phéromones sur des paires d'objets, indépendamment de l'ordre d'insertion.
Une synthèse réalisée par des chercheurs tunisiens et français a montré que l'algorithme qui consiste à laisser des traces sur les paires d'objets successivement sélectionnés s'avère moins efficace que les variantes qui se focalisent sur un objet ou des paires quelconques[10]. Les améliorations restent toutefois possibles puisque ces algorithmes pourraient être combinés à d'autres métaheuristiques afin de s'approcher de la solution optimale.
Résolution exacte[modifier | modifier le code]
Le problème du sac à dos, dans sa version classique, a été étudié en profondeur. Il existe donc de nombreuses méthodes aujourd'hui pour le résoudre. La plupart de ces méthodes correspondent à une version améliorée d'une des méthodes suivantes.
Programmation dynamique[modifier | modifier le code]
Le problème du sac à dos possède la propriété de sous-structure optimale, c'est-à-dire que l'on peut construire la solution optimale du problème à i variables à partir du problème à i–1 variables. Cette propriété permet d'utiliser une méthode de résolution par programmation dynamique.
On notera KP(i,c) le problème réduit à i variables et à contenance c. L'idée est la suivante :
Étant donné une variable i et une contenance c, les solutions optimales de KP(i,c) sont soit :
- les solutions optimales du problème à i–1 variables avec la même contenance c (c.-à-d. KP(i–1,c)), auxquelles on ajoute ;
- les solutions optimales du problème à i–1 variables avec la contenance c - wi (c.-à-d. KP(i–1,c – wi)), auxquelles on ajoute .
Le problème du sac à dos à zéro variable (KP(0,*)) a une solution optimale de valeur nulle.
On construit alors un tableau T[i,c] contenant la valeur des solutions optimales de tout problème KP(i,c) de la manière suivante :
pour c de 0 à W faire
T[0,c] := 0
fin pour
pour i de 1 à n faire
pour c de 0 à W faire
si c>=w[i] alors
T[i,c] := max(T[i-1,c], T[i-1, c-w[i]] + p[i])
sinon
T[i,c] := T[i-1,c]
fin si
fin pour
fin pour
Une fois le tableau construit, il suffit de démarrer de la case de T[n,W] et de déduire l'état des objets en remontant jusqu'à une case T[0,*].
| Capacité du sac | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Boîtes | Valeur du sac | ||||||||||||||||
| Valeur | Poids | ||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 5 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 7 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 6 | 6 |
| 7 | 12 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 7 | 7 | 8 | 8 |
| 10 | 9 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 10 | 10 | 11 | 11 | 11 | 12 | 12 |
Cet algorithme a une complexité temporelle et spatiale en O(nW). Cependant, en ajoutant un algorithme de type diviser pour régner, on peut ramener la consommation de mémoire à O(n + W)[11], voire, si seule la valeur de la solution optimale est importante, à O(W). Il a deux avantages :
- rapide si les poids sont entiers, et la capacité du sac modérée.
- pas besoin de trier les variables.
et un inconvénient :
- gourmand en mémoire (donc pas de résolution de problèmes de grande taille).
Il est à noter que cet algorithme ne s’exécute pas en temps polynomial par rapport à la taille de l'entrée. En effet la complexité étant proportionnelle à la capacité du sac W, elle est exponentielle par rapport à son codage. Si les poids des objets sont décimaux, cela oblige à multiplier les poids des objets et la capacité du sac afin de les rendre entiers. Cette opération peut alors rendre l'algorithme très lent.
Cette approche vient de Garfinkel et Nemhauser (1972)[12].
Procédure de séparation et d'évaluation[modifier | modifier le code]
Comme tout problème combinatoire, le problème de sac à dos peut être résolu à l'aide d'une procédure de séparation et d'évaluation (PSE). La fonction d'évaluation d'un nœud consiste souvent à résoudre le problème en variables continues (voir plus bas). L'implémentation proposée par Martello et Toth (1990)[13] est devenue une référence. Elle se distingue par :
- une évaluation des nœuds améliorée ;
- une recherche locale lorsque la dernière variable ajoutée au sac a amené à un échec ;
- la complexité considérable du code source.
L'avantage de cette méthode est la faible consommation de mémoire.
Approches hybrides[modifier | modifier le code]
L'approche hybride n'est pas réellement une nouvelle méthode de résolution. Elle consiste simplement à combiner les deux méthodes précédentes afin d'en tirer tous les avantages. Typiquement, on va appliquer une PSE jusqu'à une profondeur de recherche où le sous-problème sera jugé assez petit pour pouvoir être résolu par programmation dynamique.
Les précurseurs de cette approche sont Plateau et Elkihel (1985)[14], suivis par Martello et Toth (1990)[13]. Il y a eu d'autres améliorations depuis.
Variantes[modifier | modifier le code]
Le problème présenté jusqu'ici est, plus précisément, le problème de sac à dos en variables binaires (01KP). Il s'agit en fait d'une variante parmi d'autres. Cette section présente ces différentes variantes. Les particularités se font sur le domaine des variables, le nombre de valeurs des objets, le nombre de dimensions du sac, etc. Ces particularités peuvent aussi être combinées.
Variables continues[modifier | modifier le code]
Le problème du sac à dos en variables continues (LKP) est obtenu en enlevant la contrainte d'intégrité sur les variables. C’est-à-dire que l'on s'autorise à ne prendre qu'une fraction des objets dans le sac à dos : . LKP appartient à la classe de complexité P.
Voici un algorithme permettant de calculer une solution optimale du problème LKP :
trier les objets en ordre décroissant d'efficacité i := 1 w_dispo := W tant que w_dispo >= w[i] faire x[i] := 1 w_dispo := w_dispo - w[i] i := i + 1 fin tant que x[i] := w_dispo / w[i] tant que i < n faire i := i + 1 x[i] := 0 fin tant que
On remarquera que la valeur de la solution optimale de LKP est au plus égale au double de la valeur de la solution optimale du problème KP correspondant :
Variables entières[modifier | modifier le code]
Dans le problème de sac à dos en variables entières, on considère que l'on a plusieurs exemplaires de chaque objet. Le problème consiste donc à trouver le nombre d'exemplaires à prendre pour chacun.
Si le nombre d'exemplaires est limité, on parlera de sac à dos borné (BKP), sinon on parlera de sac à dos non borné (UKP). Le problème BKP peut être transformé en 01KP sans difficulté.
Sac à dos multidimensionnel[modifier | modifier le code]
On considère ici que le sac à dos a d dimensions, avec d > 0 (d-KP). Par exemple, on peut imaginer une boîte. Chaque objet a trois dimensions, et il ne faut déborder sur aucune des dimensions. La contrainte (1) est alors remplacée par :
Utilisation pratique[modifier | modifier le code]
En pratique, la version multidimensionnelle peut servir à modéliser et résoudre le problème du remplissage d'un container dont le volume et la charge maximale sont limitées.
Un autre exemple est celui de la gestion de personnel. Dans une version simplifiée, on estime la productivité ou la compétence de chaque personne (son « poids » dans le problème), et on lui attribue d'autres variables : son coût et sa disponibilité. Chacun de ces paramètres représente une dimension du sac à dos. On définit finalement les contraintes liées à son projet eu égard aux paramètres précédents, à savoir au budget disponible et au temps imparti pour réaliser le travail. La résolution permet de déterminer quelles personnes doivent être retenues pour réaliser le projet.
Sac à dos multi-objectif[modifier | modifier le code]
Une variante du problème consiste, à partir d'objets ayant plusieurs valeurs, à maximiser plusieurs fonctions objectifs, c'est le problème du sac à dos multi-objectif (MOKP). On rentre donc dans le domaine de l'optimisation multi-objectif.
Par exemple, supposons qu'on lance une société spécialisée dans les croisières. Pour se faire connaître, on décide d'inviter des gens célèbres à bord du plus beau bateau. Ce bateau ne peut supporter plus d'une tonne de passagers (ce sera la constante W). Chaque passager a une masse (wi), apporte de la publicité par sa popularité (p1
i : indice de popularité) et demande un salaire (p2
i : salaire négatif). On cherche naturellement à maximiser la publicité apportée et minimiser le salaire total à payer (maximiser le salaire négatif). De plus on veut avoir un maximum de gens sur le bateau (p3
i = 1). Il y a donc trois sommes à maximiser.
En termes mathématiques, on cherche le vecteur X de gens célèbres satisfaisant le problème :
- (on veut une popularité maximale)
- (minimiser le salaire à payer, soit maximiser le salaire négatif) ;
- (avoir un maximum de gens sur le bateau)
sous contraintes
- : le bateau ne doit pas couler.
D'une manière générale, on remplace la fonction objectif du problème initial par une famille de fonctions objectifs :
Sac à dos quadratique[modifier | modifier le code]
Le problème de sac à dos quadratique est noté QKP. On a ici un gain gij supplémentaire lorsque deux objets (i et j) sont pris simultanément. Par exemple, disons qu'on souhaite maximiser la qualité du café lors d'une expédition avec un sac à dos. On peut comprendre qu'il est plus intéressant d'apporter une cuillère et un sucre plutôt qu'un seul des deux.
La fonction objectif s'écrit alors :
Problème de la somme de sous-ensembles ou du subset sum[modifier | modifier le code]
La particularité du problème de la somme de sous-ensembles (en anglais : subset sum) est que la valeur et le poids des objets sont identiques (pi = wi). C'est un problème important du domaine de la cryptographie, utilisé dans plusieurs systèmes de génération de clé publique.
Sac à dos à choix multiple[modifier | modifier le code]
Dans le problème de sac à dos à choix multiple (MCKP), les objets sont regroupés en classes, et il ne faut prendre qu'un seul représentant pour chaque classe.
Par exemple, on est en train de confectionner votre boîte à outils. Si on a cinq clés à molette, on peut soit choisir la plus légère, afin de prendre un marteau performant, ou alors choisir la clé la plus performante et un marteau bas de gamme, ou alors faire un compromis. L'idée générale est qu'on ne peut pas prendre plus d'une clé, ni plus d'un marteau.
Si les objets sont rangés en k classes, on notera l'ensemble des indices des objets appartenant à la classe j. On considère, bien entendu, qu'un objet n'appartient qu'à une unique classe. La formulation du problème devient :
sous contraintes :
- (on ne dépasse pas la capacité du sac) ;
- (on choisit au plus un représentant de chaque classe).
Sac à dos multiple[modifier | modifier le code]
Le problème de sac à dos multiple (MKP) consiste à répartir un ensemble d'objets dans plusieurs sacs à dos de capacités différentes. C'est un problème analogue à celui du problème de bin packing mais sans la contrainte d'avoir tous les objets sockés.
Si on a k sacs à dos, on notera si l'objet i est placé dans le sac j. La formulation du problème devient :
sous contraintes
- (on ne dépasse pas la capacité des sacs) ;
- (un objet n'est mis que dans un sac).
Il existe une variante de ce problème dans laquelle tous les sacs ont la même capacité, on le note MKP-I.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
(en) Hans Kellerer, Ulright Pferschy et David Pisinger, Knapsack Problems, Springer, 2004 (ISBN 3-540-40286-1).
Notes et références[modifier | modifier le code]
- Nawal Cherfi, « Méthodes de résolution hybrides pour les problèmes de type knapsack », sur HAL, , Thèse de doctorat - Université Panthéon-Sorbonne - Paris I.
- (en) G. B. Mathews, « On the partition of numbers », Proc. London Math. Soc., vol. 28, , p. 486-490.
- (en) Public Key Cryptography, dans la partie « History » d'un projet de Eric Robert's Sophomore College class "The Intellectual Excitement of Computer Science" à l'université Stanford. La publication correspondante est : R.C. Merkle et M.E. Hellman, Hiding Information and Receipts in Trap Door Knapsacks, Internal Symposium on Information Theory, université Cornell, Ithaca, New York, octobre 1977.
- Pascal Boyer, Petit compagnon des nombres et de leurs applications, Paris, Calvage et Mounet, , 648 p. (ISBN 978-2-916352-75-6), VI. Cryptographie, chap. 6 (« La méthode du sac à dos »), p. 538-539.
- (en) A. Shamir, A Polynomial-Time Algorithm for Breaking the Basic Merkle-Hellman Cryptosystem, IEEE Transactions on Information Theory, Vol. IT-30, p. 699-704, 1984. (Première publication en avril 1982.)
- (en) Knapsack Encryption Scheme Broken, « Math Matrix », département de mathématiques de l'université d'État de l'Ohio,v1985, vol. 1, n° 3.
- (en) S. Vaudenay, Cryptanalysis of the Chor-Rivest Cryptosystem.
- Voir par exemple (en) Kurt Eisemann, « The trim problem », Management Science, INFORMS, vol. 3, no 3, , p. 279-284.
- (en) Michail G. Lagoudakis, The 0-1 Knapsack Problem - An Introductory Survey, 1996.
- (fr) Optimisation par colonies de fourmis pour le problème du sac à dos multidimensionnel.
- (en) U. Pferschy, « Dynamic programming revisited: improving knapsack algorithms », Computing. Archives for Scientific Computing, vol. 63, no 4, , p. 419-430 (lire en ligne).
- (en) R. S. Garfinkel et G. L. Nemhauser, Integer Pogramming, New York, John Wiley & Sons, (ISBN 978-0-471-29195-4).
- (en) Silvano Martello et Paolo Toth, Knapsack Problems : Algorithms and Computer Implementations, John Wiley & Sons, , 296 p. (ISBN 978-0-471-92420-3).
- (en) Gérard Plateau et Moussa Elkihel, « A hybrid method for the 0-1 knapsack problem », Methods Oper. Res., vol. 49, , p. 277-293.




































![{\displaystyle x_{i}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a32830173af0dc0eaf16f580cc75ef2f78b4f15e)















