Lunule (géométrie)
|

|

|
|
|
|
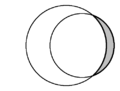
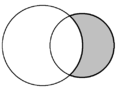
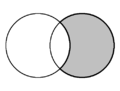
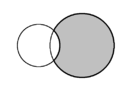
| En géométrie plane, la forme en croissant formée par deux disques s'intersectant est appelée "lunule". Au sein de chaque schéma, deux lunules sont présentes et l’une est grisée. | ||
En géométrie plane, une lunule est la surface concave-convexe délimitée par deux arcs de cercles (alors que la surface convexe-convexe délimitée par deux arcs de cercles est la version plane d'une lentille bi-convexe).
Le mot lunule vient de luna, le mot latin désignant la Lune, qui vue de la Terre ressemble à une lunule entre la nouvelle lune et le premier quartier ainsi qu'entre le dernier quartier et la prochaine nouvelle lune (en réalité le croissant de lune est délimité par un cercle et une ellipse concentriques[1]).
Aire
[modifier | modifier le code]L'aire d'une lunule formée par deux cercles de rayons R et r (R > r) dont les centres sont distants de d est de[2]
avec
qui correspond à l'aire d'un triangle de côtés R, r, et d calculée par la formule de Héron. La formule se déduit de la loi des cosinus.
Exemples
[modifier | modifier le code]Au Ve siècle avant notre ère, Hippocrate de Chios a montré que la quadrature de certaines lunules à la règle et au compas est possible, c'est le théorème des deux lunules.
Voir aussi
[modifier | modifier le code]Notes et références
[modifier | modifier le code]- « Pour dessiner un croissant de lune, est-il correct de tracer deux arcs de cercles? », sur www.deleze.name (consulté le )
- (en) Eric W. Weisstein, « Lune », sur MathWorld


