Nombre de Bernoulli
En mathématiques, les nombres de Bernoulli, notés Bn (ou parfois bn pour ne pas les confondre avec les polynômes de Bernoulli ou avec les nombres de Bell), constituent une suite de nombres rationnels.
Ces nombres ont d'abord été étudiés par Jacques Bernoulli (ce qui a conduit Abraham de Moivre à leur donner le nom que nous connaissons aujourd'hui) en cherchant des formules pour exprimer les sommes du type
Pour des valeurs entières de m, cette somme s'écrit comme un polynôme de la variable n dont les premiers termes sont :
Les premiers nombres de Bernoulli sont donnés par la table suivante :
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bn | 1 | –12 | 16 | 0 | –130 | 0 | 142 | 0 | –130 | 0 | 566 | 0 | –6912730 | 0 | 76 |
On peut les définir par l'intermédiaire du développement en série entière (convergent si |x| < 2π) :
Les nombres de Bernoulli apparaissent dans de très nombreuses applications, depuis la formule d'Euler-Maclaurin :
ou les sommes définissant la fonction zêta de Riemann, dues à Leonhard Euler :
jusqu'à l'approche par Kummer du dernier théorème de Fermat.

Les nombres A = 16, B = –130, C = 142, D = – 130, ... apparaissent dans Ars Conjectandi de Bernoulli, 1713, page 97.
Les nombres de Bernoulli avec au lieu de sont la transformée binomiale des premiers et s'obtiennent à partir des nombres de Worpitzky ou, ce qui est équivalent, en appliquant l'algorithme d'Akiyama-Tanigawa[1] à 1/(n+1). À la suite de l'article « The Bernoulli Manifesto » de Peter Luschny, Donald Knuth a adopté la valeur , aussi dans les récentes réimpressions du livre Concrete Mathematics[2],[3] ; Knuth présente les nouvelles versions dans un texte à part[4].
Histoire[modifier | modifier le code]
Les nombres de Bernoulli ont été découverts à peu près en même temps et indépendamment par le mathématicien suisse Jacques Bernoulli, dont ils portent le nom, et par le mathématicien japonais Seki Takakazu. La découverte de Seki a été publiée à titre posthume en 1712[5] dans son ouvrage Katsuyō Sanpō ; celle de Bernoulli, également à titre posthume, dans son Ars Conjectandi publié en 1713. Ada Lovelace, en 1842, traduisant et annotant une description de la machine analytique de Babbage publiée par le mathématicien italien Louis-Frédéric Ménabréa en français dans un journal suisse[6], décrit dans la note G un algorithme permettant de générer des nombres de Bernoulli avec cette machine[7]. Par conséquent, les nombres de Bernoulli ont la particularité de faire l'objet du premier programme informatique complexe publié[8].

Introduction : sommes de puissances[modifier | modifier le code]
Jacques Bernoulli connaissait quelques formules comme[9],[10],[11] :
Bernoulli observa que l'expression
est toujours un polynôme en n, de degré m + 1, de terme constant nul, dont le monôme dominant (de degré m + 1) est nm+1m+1 et le monôme de degré m est, si m > 0[12], –12nm.
On démontre (voir plus bas le paragraphe « Formules de récurrence ») que plus généralement, pour 0 ≤ k ≤ m, le coefficient de nm+1–k est le produit de m!/(m + 1 – k)! par un nombre rationnel Bk qui dépend seulement de k et pas de m. On peut donc définir les nombres de Bernoulli Bk par :
En particulier, le coefficient de n dans le polynôme Sm(n) est le nombre Bm.
Premiers nombres de Bernoulli[modifier | modifier le code]
En donnant à m la valeur 0, on obtient (avec 00 = 1) : pour tout entier n > 0,
ce qui montre que B0 = 1.
En donnant à m la valeur 1, on obtient :
ce qui confirme que B0 = 1 et montre que B1 = –1/2.
En donnant à m la valeur 2, on obtient :
ce qui montre de plus que B2 = 1/6.
En donnant à m la valeur 3, on obtient :
ce qui montre aussi que B3 = 0.
Calcul des nombres de Bernoulli par récurrence[modifier | modifier le code]
À partir de la condition initiale B0 = 1, on peut calculer les nombres de Bernoulli par récurrence en utilisant le fait que
ce qui peut se voir comme une relation de récurrence[12] :
Cette suite d'équations linéaires[13]
- etc.
donne successivement B1 = –1/2, B2 = 1/6, B3 = 0, B4 = –1/30, etc. Par exemple, le détail du calcul de B4 est :
Lien avec les polynômes de Bernoulli[modifier | modifier le code]
Les polynômes de Bernoulli Bm(X) sont reliés aux nombres de Bernoulli par
Ils vérifient les relations :
- ;
- ;
- ;
- Bm (0) = Bm si m ≥ 0 (le terme constant du polynôme de Bernoulli est égal au nombre de Bernoulli de même indice) ;
- Bm (1) = Bm si m ≠ 1.
Les polynômes Sm(n) sont également liés aux polynômes de Bernoulli :
De
on déduit que
Par conséquent, les polynômes Sm sont les primitives des polynômes de Bernoulli qui s'annulent en zéro :
Autres conventions et notations utilisées pour définir les nombres de Bernoulli[modifier | modifier le code]
On utilise parfois la notation bn pour distinguer les nombres de Bernoulli des nombres de Bell.
La définition employée dans cet article vérifie Bm = Bm(0) où Bm(x) désigne le polynôme de Bernoulli.
On rencontre également la convention Bm = Bm(1), où Bm(x) désigne le polynôme de Bernoulli.
Les deux conventions ne diffèrent que pour le signe de B1 ; on a :
Une autre notation, utilisée en topologie[14], est de considérer les termes pairs sans leur signe (on a b2k = (–1)k–1|b2k|) :
Définition par une fonction génératrice[modifier | modifier le code]
Les nombres de Bernoulli peuvent aussi être définis par l'intermédiaire d'une fonction génératrice. La série génératrice exponentielle associée à la suite est x / (ex – 1), de telle sorte que
pour tout x de valeur absolue inférieure à 2π (le rayon de convergence de cette série entière).
Cette définition peut être montrée équivalente à la précédente à l'aide d'un raisonnement par récurrence : le premier terme de la série est clairement B0 (par prolongement par continuité).
- Pour obtenir la relation de récurrence, on multiplie les deux côtés de l'équation par ex – 1. Alors, en utilisant les séries de Taylor pour la fonction exponentielle,
En développant ceci en produit de Cauchy et en réarrangeant légèrement, on obtient
Il est clair, à partir de cette dernière égalité, que les coefficients dans cette série entière satisfont la même relation de récurrence que les nombres de Bernoulli (voir paragraphe : « Calcul des nombres de Bernoulli par récurrence »).
Valeurs[modifier | modifier le code]
Les premiers nombres de Bernoulli sont les suivants :
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Signe des nombres de Bernoulli[modifier | modifier le code]
À l'aide de la fonction génératrice, on peut démontrer que Bn = 0 lorsque n est impair et différent de 1, et que les signes des Bn alternent pour n pair. On a donc :
Formules de récurrence[modifier | modifier le code]
On justifie ici la définition des nombres de Bernoulli annoncée dans l'introduction. Repartons des sommes
pour tous entiers naturels m et n (en particulier, Sm(0) = 0).
On remarque que (d'après la formule du binôme après réindexation) :
et l'on obtient finalement :
ce qu'on peut voir comme une définition des Sm(n) par récurrence sur m (incluant l'initialisation S0(n) = n). C'est cette approche qui permet de démontrer par récurrence que les coefficients de Sm(n) sont bien de la forme donnée dans l'introduction : .
Pour tout j ≥ 0, notons Bj le coefficient de n dans Sj(n), , et déduisons de la formule de récurrence des Sm(n) ci-dessus, par récurrence sur j, que le coefficient ck,j de nj+1–k dans Sj(n) est le produit de j!/(j + 1 – k)! par Bk/k! non seulement pour k = j, mais aussi pour tout entier naturel k < j (ce qui est immédiat pour k = 0). En supposant la propriété vraie pour tout j < m, on trouve comme coefficient cm,i de nm+1–i dans Sm(n), pour 0 < i < m :
la première égalité résultant de l'hypothèse de récurrence et la dernière égalité résultant du § Calcul des nombres de Bernoulli par récurrence :
Les nombres de Bernoulli et la fonction zêta de Riemann[modifier | modifier le code]
La première relation a été obtenue par Leonhard Euler[15],[16] sous la forme suivante
(On peut l'obtenir comme corollaire du calcul de la série de Fourier des polynômes de Bernoulli.)
La relation s'écrit en utilisant la fonction zêta de Riemann :
relation qui entraîne (pour n > 0) :
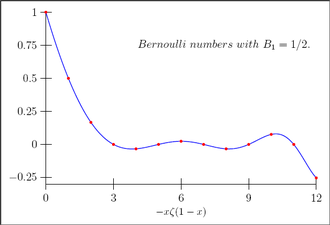
L'apparition de B12 = –6912730 semble montrer que les valeurs des nombres de Bernoulli ne peuvent pas être décrites simplement ; en fait, ce sont essentiellement des valeurs de la fonction ζ de Riemann pour des valeurs entières négatives de la variable, puisque
et l'on sait que cette dernière est d'étude difficile (voir hypothèse de Riemann).
Il est possible d'exprimer les nombres de Bernoulli grâce à la fonction zêta de Riemann de la façon suivante :
et
En particulier :
Comportement asymptotique de |B2n|[modifier | modifier le code]
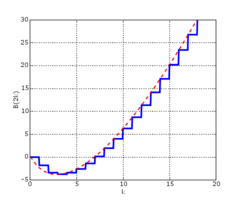
On a l'égalité suivante pour les nombres de Bernoulli d'indice pair :
De la définition de la fonction zêta de Riemann, on déduit que ζ(2n) > 1 (si n > 0,5). Par conséquent, on a l'encadrement :
De l'inégalité (si n > 0), on déduit que : (si n > 0) , donc :
Par conséquent :
On a l'équivalent :
En utilisant la formule de Stirling pour écrire un équivalent de (2n)!, on démontre l'équivalent quand n tend vers l'infini :
Applications en analyse[modifier | modifier le code]
Les nombres de Bernoulli apparaissent dans le développement en série de Taylor des fonctions tangentes (circulaire et hyperbolique), dans la formule d'Euler-Maclaurin ainsi que dans des expressions de certaines valeurs de la fonction zêta de Riemann.
Formule d'Euler-Maclaurin[modifier | modifier le code]
Soit a un nombre réel et N un entier naturel. Si f est une application de classe (avec k ≥ 1) sur [a, a + N].
avec
où est la fonction périodique de période 1 égale à Bk(x), le polynôme de Bernoulli d'indice k, sur l'intervalle [0 ; 1[.
où ⌊t⌋ désigne la partie entière de t.
Développements en série de Taylor[modifier | modifier le code]
À partir de la fonction génératrice,
on démontre les formules suivantes[17] :
|
|
|
Les nombres sont des nombres entiers appelés nombres tangents ou nombres d'Euler de deuxième espèce[18].
On a le développement suivant :
Développements en série des nombres de Bernoulli[modifier | modifier le code]
Propriétés arithmétiques[modifier | modifier le code]
Les nombres de Bernoulli et les groupes de classes d'idéaux[modifier | modifier le code]
Les propriétés de divisibilité des numérateurs des nombres de Bernoulli sont liées aux groupes des classes d'idéaux des corps cyclotomiques par un théorème de Kummer. En 1847, Kummer démontrait que le dernier théorème de Fermat était vrai pour un certain ensemble de nombres premiers appelés nombres premiers réguliers. On dit qu'un nombre premier impair est « régulier » s'il ne divise pas le nombre de classes de ℚ(ζp), sinon on dit que p est irrégulier. Kummer découvrit un lien avec les propriétés de divisibilité des numérateurs des nombres de Bernoulli : un nombre premier p impair est régulier si, et seulement si, p ne divise le numérateur d'aucun des nombres B2, B4, … , Bp–3. Le nombre premier 3 est régulier. Les premiers nombres premiers irréguliers sont : 37, 59, 67, 101, 103, 149 et 157. Si p est régulier, alors l'équation xp + yp = zp n'a pas de solution entière (à part 1, 0 et 1). C'est la raison pour laquelle les nombres de Bernoulli possèdent des propriétés arithmétiques profondes.
Le théorème de Kummer a été renforcé par le théorème de Herbrand-Ribet. Les nombres de Bernoulli sont également liés aux nombres de classes des corps quadratiques par la congruence d'Ankeny-Artin-Chowla.
Liens avec la K-théorie algébrique[modifier | modifier le code]
Il existe aussi un lien avec la K-théorie algébrique : une conséquence de la conjecture de Quillen-Lichtenbaum (en) est le résultat suivant[19] :
- si n = 4k – 2 et ck est le numérateur de B2k/k, alors l'ordre de Kn(ℤ) est |ck| si k est pair (n ≡ 6 mod 8), et 2ck si k est impair (n ≡ 2 mod 8) ;
- si n = 4k – 1 et dk est le dénominateur de B2k/k, alors l'ordre de Kn(ℤ) est 4dk si k est pair (n ≡ 7 mod 8), et 8dk si k est impair (n ≡ 3 mod 8).
Théorème de von Staudt-Clausen[modifier | modifier le code]
Le théorème de von Staudt-Clausen est aussi relié à la divisibilité. Il énonce ceci :
- si l'on ajoute à Bn les inverses 1⁄p pour chaque nombre premier p tel que p − 1 divise n, on obtient, si n = 1 ou n est pair non nul, un nombre entier.
Ce fait permet immédiatement de caractériser les dénominateurs des nombres de Bernoulli non entiers Bn comme le produit de tous les nombres premiers p tels que p − 1 divise n. En conséquence, si 2n est un entier non nul, le dénominateur du nombre de Bernoulli B2n est sans carré et divisible par 6.
- Exemples
La propriété se traduit par : pB2m ≡ −1 mod p si p – 1 divise 2m. (La notation a ≡ b mod p signifie que p divise le numérateur de a – b mais pas son dénominateur.)
La conjecture d'Agoh-Giuga postule que p est un nombre premier si et seulement si pBp−1 ≡ −1 mod p.
Continuité p-adique[modifier | modifier le code]
Une propriété de congruence, dite congruence de Kummer, spécialement importante des nombres de Bernoulli peut être caractérisée comme une propriété de continuité p-adique. Si p, m et n sont des nombres entiers positifs tels que m et n ne sont pas divisibles par p − 1 et alors
(La notation a ≡ b mod pk signifie que pk divise le numérateur de a – b mais pas son dénominateur.)
Puisque Bn = –nζ(1–n) ceci peut être aussi écrit
où u = 1 − m et v = 1 − n, si bien que u et v sont négatifs et non congrus à 1 mod p – 1.
Ceci nous indique que la fonction zêta de Riemann avec 1 − p−s omis dans la formule du produit eulérien, est continue pour les nombres p-adiques sur les nombres entiers négatifs congrus mod p – 1 à un entier fixé , et peut donc être étendue en une fonction continue ζp(s) sur l'anneau topologique ℤp des entiers p-adiques : la fonction zêta p-adique.
Utilisation en topologie[modifier | modifier le code]
La formule de Kervaire-Milnor pour l'ordre du groupe cyclique des classes de difféomorphismes des (4n − 1)-sphères exotiques qui bordent des variétés parallélisables pour n ≥ 2 fait intervenir les nombres de Bernoulli : si Nn est le numérateur de B4n/n, alors le nombre de ces classes de difféomorphisme de sphères exotiques est
La formule donnée dans les articles de topologie diffère car les topologues utilisent une convention différente pour nommer les nombres de Bernoulli (ils notent Bn la suite 1, 1/6, 1/30…).
Formules explicites[modifier | modifier le code]
On peut en fait également définir les Bn sans récurrence : utilisant les nombres de Stirling (de deuxième espèce), on a (pour n > 1)[20]
d'où (en utilisant les formules explicites pour les nombres de Stirling et en simplifiant)
On trouve assez souvent dans la littérature l'affirmation selon laquelle des formules explicites pour les nombres de Bernoulli n'existent pas[21] ; les deux dernières équations montrent qu'il n'en est rien. En fait, dès 1893, Louis Saalschütz (de) recensait un total de 38 formules explicites, donnant généralement des références bien plus anciennes.
Identités remarquables[modifier | modifier le code]
Relations de Ramanujan[modifier | modifier le code]
Les trois relations suivantes, dues à Ramanujan, fournissent une méthode plus efficace pour le calcul des nombres de Bernoulli :
Une identité de Carlitz[modifier | modifier le code]
Si m et n sont des entiers strictement positifs :
Notes et références[modifier | modifier le code]
- Masanobu Kaneko, « The Akiyama-Tanigawa algorithm for Bernoulli numbers », Journal of Integer Sequences, Vol. 3 (2000), vol. 3, , article no 00.2.9 (lire en ligne, consulté le ).
- Knuth:Recent News
- « the new (34th) printing of Concrete Mathematics, released in January 2022 contains the much more extensive changes that are needed to tell a more comprehensive story »
- Replacement pages.
- (en) Tomoko L. Kitagawa, « The Origin of the Bernoulli Numbers: Mathematics in Basel and Edo in the Early Eighteenth Century », The Mathematical Intelligencer, (ISSN 0343-6993, DOI 10.1007/s00283-021-10072-y
 , lire en ligne)
, lire en ligne)
- Louis-Frédéric_Ménabréa, « Notions sur la machine analytique de M. Charles Babbage », Bibliothèque universelle de Genève, vol. 41, , p. 352-376 (lire en ligne, consulté le )
- (en) Louis-Frédéric Ménabréa et Ada King, comtesse de Lovelace, Sketch of the Analytical Engine invented by Charles Babbage, Esq. By L. F. Menabrea of Turin, officer of the military engineers, with notes by the translator, Londres, Richard and John E. Taylor, (lire en ligne), p. 722
- Anne-Marie Kermarrec, « La visionnaire Ada Lovelace », Le Monde - Blog Binaire, (lire en ligne)
- (en) Kenneth Ireland et Michael Rosen, A Classical Introduction to Modern Number Theory, Springer, coll. « GTM » (no 84), (réimpr. 1998), 2e éd., 389 p. (ISBN 978-0-387-97329-6, lire en ligne), p. 228.
- (en) Alain M. Robert (en), A Course in p-adic Analysis, Springer, coll. « GTM » (no 198), (lire en ligne), p. 273.
- (en) Henri Cohen, Number Theory, vol. II : Analytic and Modern Tools, Springer, (lire en ligne), p. 31.
- Ireland et Rosen 1990, p. 229.
- Ireland et Rosen 1990, p. 230.
- Voir aussi Jean-Pierre Serre, Cours d'arithmétique, [détail des éditions], p. 147.
- (en) Ed Sandifer, How Euler did it – Bernoulli numbers[PDF], septembre 2005.
- (la) E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum (1755), partie II, chap. 5, traduction en anglais[PDF] par David Pengelley (2000).
- Cohen 2007, p. 5.
- Alain Bouvier, Michel George et François Le Lionnais, Dictionnaire des mathématiques, PUF, 2001, 6e édition, p. 320.
- (en) Charles Weibel (en), « Algebraic K-theory of rings of integers in local and global fields », dans Handbook of K-theory, vol. 1, Springer, (lire en ligne [PDF]).
- (en) Ronald Graham, Donald Knuth et Oren Patashnik, Concrete Mathematics, p. 289 (eq. 6.99) ; on trouvera également une démonstration de cette formule sur Wikiversité.
- (en) Henry W. Gould (en), « Explicit formulas for Bernoulli numbers », Amer. Math. Monthly, vol. 79, , p. 44-51.
- (en) L. Carlitz, « Bernoulli Numbers », Fibonacci Quart., vol. 6, no 3, , p. 71-85 (lire en ligne).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
John H. Conway et Richard K. Guy, Le Livre des nombres, Eyrolles, 1998 (ISBN 2-212-03638-8)
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (en) « Bernoulli numbers », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
- Les 498 premiers nombres de Bernoulli sur le Projet Gutenberg
- (en) The Bernoulli Number Page
- (en) Eric W. Weisstein, « Bernoulli Number », sur MathWorld
- (en) Calcul et développement asymptotique des nombres de Bernoulli, par P. Luschny sur le site de l'OEIS












































![{\displaystyle B_{2n}=(-1)^{n+1}{\frac {2(2n)!}{(2\pi )^{2n}}}\left[1+{\frac {1}{2^{2n}}}+{\frac {1}{3^{2n}}}+{\frac {1}{4^{2n}}}+\cdots \;\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b800ebe6859133a505f8634cc2ab6da61605e5)
















































