Dimension fractale

En géométrie fractale, la dimension fractale, D, est une grandeur qui a vocation à traduire la façon qu'a un ensemble fractal de remplir l'espace, à toutes les échelles. Dans le cas des fractales, elle est non entière et supérieure à la dimension topologique.
Ce terme est un terme générique qui recouvre plusieurs définitions. Chacune peut donner des résultats différents selon l'ensemble considéré, il est donc essentiel de mentionner la définition utilisée lorsqu'on valorise la dimension fractale d'un ensemble. Les définitions les plus importantes sont la dimension de Hausdorff, la dimension de Minkowski-Bouligand (ou "box-counting"), et la dimension de corrélation.
Dans le cas d'ensembles fractals simples (auto-similarité stricte, notamment) on conjecture[1] que ces définitions donnent des résultats identiques.
Par abus de langage, on trouve parfois le terme "dimension fractale" pour désigner des grandeurs non géométriques telles que l'exposant de lois de puissance dans des lois de distribution statistiques ou des séries temporelles, invariantes d'échelle, notamment en finance[2].
Approche didactique[modifier | modifier le code]

Les figures géométriques usuelles ont une dimension entière :
- La dimension D d'un segment, d'un cercle et d'une courbe régulière est de 1. Sa longueur est multipliée par lorsque sa taille double.
- La dimension D d'une surface simple et bornée est de 2. Elle a une aire finie et cette aire est multipliée par lorsque sa taille double.
- La dimension D d'un volume simple et borné dans l'espace est de 3. Il a un volume fini et ce volume est multiplié par lorsque sa taille double.
Si D est la dimension d'un objet, alors la mesure de cet objet est multipliée par lorsque la taille de cet objet est multipliée par .

Or, par exemple, la longueur de la courbe de Koch est multipliée par 4 lorsque sa taille triple (en effet, cette courbe est précisément définie comme étant constituée de quatre copies d'elle-même, trois fois plus petites). Puisque , on peut considérer intuitivement qu'il s'agit d'un objet de dimension (plus précisément, ). Il ne s'agit plus d'une simple courbe unidimensionnelle, ni d'une surface, elle se situe « entre les deux ». Cette « dimension fractale », non entière, est caractéristique des ensembles fractals.
De manière simplifiée et en première approximation, un objet fractal est un objet ayant une homothétie interne, c'est-à-dire qu'une portion de l'objet est identique à l'objet complet. Considérons un exemple simple, le flocon de Koch : cette courbe est construite de manière récursive, on part d'un segment de droite, et on remplace chaque segment par un segment avec un chevron au milieu.
On répète cette opération à l'infini. Cette courbe est une ligne (donc de dimension 1, au sens ordinaire). Sa longueur est infinie, puisqu'à chaque étape on multiplie sa longueur par 4/3, et qu'il y a un nombre infini d'étapes. Pourtant, et contrairement à une droite infinie, on peut toujours trouver une courbe de longueur finie aussi proche que l'on veut de la courbe de von Koch. On peut donc dire en fait que si on trouve que la longueur de la courbe de von Koch est infinie, c'est qu'on l'évalue dans une « mauvaise » dimension, et qu'en mesurant « mieux », on aurait une mesure « utile », finie.
Nous avons besoin de revenir sur la notion d'étalon en physique :
- L'étalon de longueur est une règle de longueur fixe (dimension 1) : pour mesurer une longueur, on regarde combien de règles tiennent bout-à-bout sur la courbe ;
- L'étalon de surface est un carreau (carré) de côté fixe (dimension 2) : pour mesurer la surface, on regarde combien de carreaux on peut poser côte-à-côte sur la surface ;
- L'étalon de volume est un pavé (cube) d'arête fixe (dimension 3) : pour mesurer le volume, on regarde combien de pavés on peut empiler dans l'objet.
On ne peut évaluer la longueur que d'un objet de dimension 1 : même en prenant une règle minuscule, un point ne pourra jamais la contenir, et à l'inverse sur une surface, on peut mettre un nombre infini de règles côte-à-côte (celles-ci ont une épaisseur nulle).
De même, on ne peut évaluer l'aire que d'un objet de dimension 2 : un point ou une courbe ne pourra jamais être pavé par des carreaux (même très petits), et dans un volume, on peut empiler un nombre infini de carreaux (ceux-ci ont une épaisseur nulle).
On ne peut évaluer le volume que d'un objet à trois dimensions, puisqu'on ne peut pas mettre de pavé dans un point, une courbe ni une surface.
Ainsi, si l'on appelle do la dimension de l'objet et de celle de l'étalon, on a :
- si de > do, la mesure donne 0 : on ne peut pas mettre un seul étalon dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une aire, ce qui indique donc que sa dimension fractale est strictement inférieure à 2.
- si de < do, la mesure donne ∞ : on peut mettre autant d'étalons qu'on veut dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une longueur, ce qui indique donc que sa dimension fractale est strictement supérieure à 1.
- si de = do, la mesure peut donner (si l'objet mesuré n'est pas infini) un nombre fini, le nombre d'étalons qu'il faut pour couvrir l'objet ; notre problème est donc de trouver (si elle existe) la « bonne » dimension, celle qui nous donnera une mesure finie (si l'objet est fini).

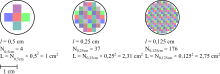

Pour faire cette mesure, la « taille » de l'étalon n'est pas sans effet. Si l'étalon est trop grand, il n'entre pas dans l'objet (la mesure est nulle), mais en prenant des étalons de plus en plus petits, on obtient (d'habitude) des mesures qui se rapprochent. Si, pour mesurer une ligne, on utilise une règle de longueur ℓ, plus ℓ est petit, plus on pourra mettre d'étalons dans l'objet à mesurer. La mesure est le produit du nombre d'étalons par la taille de l'étalon : Si l'on fait tenir Nℓ règles de longueur ℓ, la mesure sera
- M(ℓ) = Nℓ×ℓ 1
Pour un carreau de côté ℓ, l'aire du carreau sera ℓ², et si l'on couvre la surface de Nℓ carreaux, la mesure sera
- M(ℓ) = Nℓ×ℓ 2
Pour un pavé d'arête ℓ, le volume du pavé sera ℓ3, et si l'on rempli l'objet de Nℓ pavés, la mesure sera
- M(ℓ) = Nℓ×ℓ 3
On voit que la dimension est aussi l'exposant intervenant dans le calcul de la mesure.
Dans le cas d'une ligne habituelle, lorsqu'on utilise une règle de longueur ℓ divisée par deux (ou par trois, quatre, …, N), on peut mettre à peu près deux (respectivement trois, quatre, …, N) fois plus de fois l'étalon dans l'objet : la mesure ne change presque pas, et finalement, au fur et à mesure qu'on réduit la taille de l'étalon, on obtient une suite de mesures qui converge : la longueur exacte de la courbe est la limite de M(ℓ) lorsque ℓ tend vers 0, c'est un nombre réel.
Prenons l'exemple d'une surface ; lorsqu'on la pave des carreaux, on n'obtient qu'une approximation de son aire (on approche la surface par un polygone). Si l'on fait tenir Nℓ règles de longueur ℓ, la mesure sera
- M(ℓ) = Nℓ×ℓ 2
L'aire exacte de la courbe est la limite de M(ℓ) lorsque ℓ tend vers 0. Par contre
- M(ℓ) = Nℓ×ℓ 1
tend vers +∞, et
- M(ℓ) = Nℓ×ℓ 3
tend vers 0. On retrouve par le calcul ce que l'on a établi par géométrie.
Dans le cas de la courbe de von Koch, on voit bien que lorsqu'on divise l'étalon de longueur par 3, on peut mettre 4 fois plus d'étalons. Du coup, la suite de mesures de longueur
- M(ℓ/3) = Nℓ/3×(ℓ/3) 1 = 4Nℓ×ℓ 1/3 = 4/3×M(ℓ) > M(ℓ)
ne converge pas et la suite de mesures d'aire
- M(ℓ/3) = Nℓ/3×(ℓ/3)2 = 4Nℓ/3×ℓ 2/9 = 4/9×M(ℓ) < M(ℓ)
tend vers 0.
Mais il est possible d'imaginer une dimension fractionnaire, de faire varier de façon continue la « dimension ». Et de fait, pour la dimension
- do = log 4/log 3 ≈ 1,2619.
on peut faire converger la mesure pour la courbe de von Koch en prenant :
- M(ℓ) = Nℓ ×ℓ do
Les principales définitions[modifier | modifier le code]
Les définitions suivantes, les plus couramment rencontrées, abondent dans la littérature (voir les articles détaillés ou les références citées en fin d'article : Mandelbrot ou Falconer[3]).
| Définition | Applicabilité | Formule | Commentaires |
|---|---|---|---|
| Dimension de Hausdorff | la plus rigoureuse, et définie pour tout ensemble, elle est peu aisée à mettre en œuvre. | où est la mesure de Hausdorff de l'ensemble | Elle s'appuie sur une mesure, la mesure de Hausdorff. C'est la valeur critique de s pour laquelle la valeur de la mesure passe de 0 à l'infini. |
| Dimension d'homothétie (1) | Limitée aux ensembles à homothéties internes | est solution de où N est le nombre d'homothéties et rk le rapport de l'homothétie de rang k. Dans le cas de rapports identiques, elle admet une solution analytique simple (voir ci-dessous) | C'est la traduction la plus simple de la dimension de Hausdorff, applicable aux seuls ensembles fractals à homothétie interne où les homothéties qui les composent sont toutes deux à deux disjointes. Attention, cette formule n'est pas applicable dans le cas de transformations affines ou non-linéaires. |
| Dimension d'homothétie (2) | Limitée aux ensembles à homothéties internes de même rapport | où N est le nombre d'homothéties et r le rapport d'homothétie | C'est un cas particulier de solution pour l'équation générale ci-dessus. La dimension d'homothétie vaut alors le quotient logarithmique entre le nombre d'homothéties internes de l'ensemble, sur l'inverse du rapport d'homothétie. |
| Dimension de Minkowski-Bouligand ou "Box-counting" | Tout ensemble | où N(ε) est un nombre de sous-ensembles de diamètre au plus ε nécessaires pour recouvrir l'ensemble. | La plus courante et la plus simple pour mesurer numériquement la dimension d'une fractale. Elle prend pour base la couverture de l'ensemble fractal par des ensembles de taille décroissantes. S'appuie sur une notion de comptage et non de mesure, ce qui la rend moins universelle. Peut, alors, être supérieure à la dimension de Hausdorff, mais jamais inférieure. |
Autres définitions[modifier | modifier le code]
Ces définitions sont plus rares dans la littérature. Elles sont utilisées dans des contextes spécifiques (théorie du chaos, par exemple).
| Définition | Applicabilité | Formule | Commentaires |
|---|---|---|---|
| Dimension de corrélation[4] | Appliquée aux ensembles de points (attracteurs notamment) | où M est le nombre de points utilisés pour générer la fractale et gε le nombre de paires de points dont la distance mutuelle est inférieure à ε. | Dimension de Rényi d'ordre 2. Principalement utilisée en théorie du chaos pour estimer la dimension fractale d'attracteurs, représentés par un ensemble de points calculés. Elle considère le nombre de paires de points dont la distance mutuelle est inférieure à une distance donnée. Elle a pour avantage de permettre des calculs rapides et souvent en accord avec les autres méthodes de calcul. |
| Dimension d'information [5] | Appliquée aux ensembles de points (attracteurs notamment) | où N est le nombre d'hypercubes de côté qui partagent l'espace et la probabilité pour un point de tomber dans le cube de d'index i | Dimension de Rényi d'ordre 1. La dimension d'information considère l'information nécessaire pour décrire les cases occupées par les points de l'attracteur, à mesure que la taille de ces cases diminue. |
| Dimension de Rényi[6],[7] | Appliquée aux ensembles de points (attracteurs notamment) | où le numérateur est la limite de l'entropie de Rényi d'ordre α | Adapté à la mesure d'attracteurs. La dimension de Minkowski, la dimension d'information et la dimension de corrélation peuvent être vus comme des cas particuliers de dimension de Rényi d'ordre α. La dimension de Rényi pour α=0 traite toutes les parties du support de l'attracteur de manière identique. Pour de plus grandes valeurs de α, un poids plus important est donné aux parties de l'attracteur visitées le plus fréquemment. Un attracteur pour lequel les dimensions de Rényi ne sont pas toutes égales est considéré comme multifractal, ou possède une structure multifractale. |
| Dimension "packing"[3] | Tout ensemble | .... | Duale de la dimension de Hausdorff. Elle considère le maximum de boules disjointes dont le centre appartient à l'ensemble fractal et non le minimum de boules couvrant la fractale. |
| Dimension "divider"[3] | Appliquée aux courbes sans auto-intersection | ou est le plus grand nombre de points de la courbe successivement équidistants d'une longueur donnée ( tels que ) | Considère l'application répétée d'une unité de mesure de longueur de plus en plus petite (Cf illustration en tête de l'article). Utilisée par Lewis Fry Richardson pour mesurer la dimension de la côte de Grande-Bretagne. |
Relations entre dimensions[modifier | modifier le code]
On montre, dans le cas général, que : [4],[8],[3] où :
- est la dimension topologique de l'ensemble
- est la dimension de corrélation de l'ensemble (Rényi d'ordre 2)
- est la dimension d'information de l'ensemble (Rényi d'ordre 1)
- est la dimension de Hausdorff de l'ensemble (ou dimension d'homothétie)
- est la dimension de Minkowski-Bouligand de l'ensemble
- est la dimension "divider" de l'ensemble
En cas d'autosimilarité stricte, on conjecture (Schroeder, 1991) que et sont égales.
Pour un attracteur, si chaque élément de l'attracteur a une probabilité identique d'être visitée, alors et sont égales[5].
Applications et limites[modifier | modifier le code]

La mesure de la dimension fractale trouve des applications dans de nombreux domaines de recherche tels que la physique[9], l'analyse d'image[10],[11], l'acoustique[12] l'analyse des zéros de la fonction de Riemann[13] ou les processus électrochimiques[14].
L'estimation de la dimension fractale d'objets réels est très sensible au bruit et à la quantité de données disponible. On doit donc être prudent concernant la valeur obtenue.
Les définitions de dimension fractale présentées dans les sections précédentes s'entendent à la limite, lorsque ε tend vers zéro. Or cette limite n'est jamais atteinte dans le monde physique à cause des limites moléculaire ou quantique. Pour cette raison il n'existe pas d'objet physique fractal au sens strict[15].
La dimension fractale n'est, en pratique, calculée que sur un intervalle défini, généralement pour des valeurs de ε visibles (ou significatives vis-à-vis des propriétés que l'on souhaite étudier). On définira ainsi une dimension fractale apparente ou approximative.
La mesure d'une telle dimension fractale apparente utilise souvent la méthode de Minkowski-Bouligand ou méthode "box-counting" par comptage de boîtes. Elle consiste à
- mesurer les valeurs de pour différentes valeurs de ε dans l'intervalle choisi,
- puis porter ces valeurs sur un graphe donnant en fonction de . Si la figure est auto-similaire, ces points seront alignés,
- enfin déterminer la pente de cette droite, ce qui donnera la valeur de la dimension fractale recherchée.

Cette restriction peut également concerner des constructions purement géométriques. À titre de contre-exemple, dans l'illustration ci-contre, on a défini une figure fractale paradoxale ayant l'aspect de la courbe de Koch mais ayant la dimension fractale de l'ensemble de Cantor : . Elle est construite à la manière de Koch sur les premières itérations, celles concernant des intervalles de longueur visible, mais continue à l'infini avec la construction de l'ensemble triadique de Cantor. Si l'on s'en tient à l'aspect visible, on peut considérer sa dimension fractale apparente, qui vaut celle de la courbe de Koch : , sur les intervalles de ε visibles.
Cet exemple illustre par ailleurs que dimension fractale et « rugosité » apparente, concept popularisé par Mandelbrot, ne vont pas toujours de pair.
Voir aussi[modifier | modifier le code]
Notes[modifier | modifier le code]
- (en) Manferd Robert Schroeder, Fractals, Chaos, Power Laws : Minutes from an Infinite Paradise, New York, W H Freeman & Co (Sd), , 6e éd., 429 p. (ISBN 978-0-7167-2136-9, LCCN 90036763)
- Dimension fractale d'un index boursier
- (en) Kenneth Falconer, Fractal Geometry : Mathematical Foundations and Applications, Chichester, John Wiley & Sons, Ltd., 1990 & 2003, 2e éd., poche (ISBN 978-0-470-84862-3, LCCN 2004271361)
- Dimension de corrélation sur Mathworld
- Dimension d'information sur Mathworld
- Dimension de Renyi sur Scholarpedia
- Dimension de Rényi sur Mathworld
- Dimension de Minkowski sur Mathworld
- (en) B. Dubuc, J. F. Quiniou, C. Roques-Carmes, C. Tricot, and S. W. Zucker, « Evaluating the fractal dimension of profiles », Phys. Rev. A, vol. 39, , p. 1500–12 (DOI 10.1103/PhysRevA.39.1500)
- (en) P. Soille and J.-F. Rivest, « On the validity of fractal dimension measurements in image analysis », Journal of Visual Communication and Image Representation, vol. 7, , p. 217–229 (DOI 10.1006/jvci.1996.0020, lire en ligne)
- (en) Tolle, C. R., McJunkin, T. R., and Gorisch, D. J., « Suboptimal Minimum Cluster Volume Cover-Based Method for Measuring Fractal Dimension », IEEE Trans. Pattern Anal. Mach. Intell., vol. 25, no 1, , p. 32–41 (DOI 10.1109/TPAMI.2003.1159944)
- (en) P. Maragos and A. Potamianos, « Fractal dimensions of speech sounds: Computation and application to automatic speech recognition », Journal of the Acoustical Society of America, vol. 105, no 3, , p. 1925 (PMID 10089613, DOI 10.1121/1.426738)
- (en) O. Shanker, « Random matrices, generalized zeta functions and self-similarity of zero distributions », J. Phys. A: Math. Gen., vol. 39, , p. 13983–97 (DOI 10.1088/0305-4470/39/45/008)
- (en) Ali Eftekhari, « Fractal Dimension of Electrochemical Reactions », Journal of the Electrochemical Society, vol. 151, no 9, , E291–6 (DOI 10.1149/1.1773583)
- Pas plus qu'il n'existe d'objet physique strictement circulaire ou carré. Cette réserve n'est pas limitée à la géométrie fractale
Références[modifier | modifier le code]
- Benoît Mandelbrot, Les Objets fractals : forme, hasard, et dimension, Flammarion,
- Benoît Mandelbrot, Les Objets fractals, survol du langage fractal, Flammarion, 1975, 1984, 1989, 1995
- (en) Benoît Mandelbrot, « How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. », Science, New Series, vol. 156, no 3775, , p. 636-638 (DOI 10.1126/science.156.3775.636)
- (en) Kenneth Falconer, Fractal Geometry : Mathematical Foundations and Applications, Chichester, John Wiley & Sons, 1990 & 2003, 2e éd., poche (ISBN 978-0-470-84862-3, LCCN 2004271361)



































