Gnomon
Un gnomon (du lat. gnomon, onis dérivé du grec ancien γνώμων « indicateur, instrument de connaissance ») est un instrument astronomique qui visualise par son ombre les déplacements du Soleil sur la voûte céleste.
Sa forme la plus simple est un bâton planté verticalement dans le sol.
D'après Lloyd A. Brown, 1979 « L'angle de l'ombre indiquait au berger aussi bien qu'au préteur où en était l'avancée du jour, tandis que sa longueur indiquait le passage des saisons ».

Sur la simulation Povray ci-contre, l'instrument « gnomon » est la tige verticale terminée par une boule ; on peut y constater que la longueur de son ombre est infinie au lever et au coucher du Soleil, et qu'elle est la plus courte au moment où le Soleil est le plus haut dans le ciel, soit à l'instant du midi vrai (midi solaire), indiquant par là la direction Nord-Sud correspondant à la méridienne du lieu.
L'interprétation des diverses positions de l'extrémité de l'ombre d'un grand gnomon permet de définir de nombreux paramètres liés à la course annuelle et journalière du Soleil tels qu'instant de midi, ligne méridienne, points cardinaux, solstices et équinoxes, durée de l'année, etc., sans oublier les heures repérables sur un instrument d'usage, constitué au départ d'un petit gnomon et d'une table adéquate, et qui sera appelé cadran solaire.
L'histoire du gnomon remonte à l'Antiquité, que ce soit dans le bassin méditerranéen ou en Chine. Ses applications initiales ont été mises en place à cette époque.
Plus tard, au XIIIe siècle en Chine, et à partir du XVIe siècle en Occident, l'établissement d'un calendrier sans dérive excessive nécessita la connaissance de la longueur de l'année tropique avec une plus grande exactitude. Ce sera l'époque des grands gnomons associés aux méridiennes astronomiques.
De nos jours, il est parfois employé dans des applications concernant les cadrans solaires, comme déterminer l'orientation d'un mur. Mais sa plus belle utilisation est sans conteste dans le domaine de l'exploration spatiale. Des missions automatiques ont emporté dans leurs « soutes » quelques gnomons pour repérer la position du Soleil aux heures des planètes visitées.
Sens du mot[modifier | modifier le code]
Michel Serres fait remarquer la difficulté à traduire le mot gnomon. Littéralement, il signifie « qui discerne, qui règle », en renvoyant nécessairement à un objet. Cependant, Thomas L. Heath le décrit comme « ‘‘a thing enabling something to be known, observed or verified’’ (une chose permettant à quelque chose d'être connu, observé ou vérifié) »[1].
Vocabulaire[modifier | modifier le code]
Le gnomon a donné son nom à une branche de l'astronomie, la science des cadrans solaires appelée la gnomonique (lat. gnomonica), ainsi qu'aux experts en gnomonique, les gnomonistes (lat. gnominici) qui conçoivent des cadrans[2]. Le réalisateur, lui, est appelé cadranier. Souvent le gnomoniste et le cadranier ne sont qu'une seule et même personne.
- Association
- un cadran solaire, à l'origine, était constitué d'un gnomon dont l'ombre se projetait sur une table quelconque recevant des lignes horaires ;
- une méridienne est aujourd'hui l'association d'un gnomon avec une table le plus souvent plane réduite à la ligne horaire de midi ; traditionnellement l'usage du terme « méridienne » date de la Renaissance avec l'apparition des grandes méridiennes astronomiques en Italie, mais l'appellation « gnomon » pour désigner une méridienne reste d'usage assez courant, même au XXIe siècle.
- Gnomon et style
- en gnomonique, sur les cadrans antiques, indiquant des heures temporaires, l'indicateur portait et porte toujours, par convention, le nom de « gnomon »[3] ;
- sur les cadrans solaires modernes qui indiquent des heures équinoxiales, le terme à employer pour l'indicateur est « style ». Le plus souvent, le style est parallèle à l'axe de rotation de la Terre, on parle alors d'un cadran à « style polaire ». Sur certains cadrans, cependant, le style est perpendiculaire au cadran et seule son extrémité est utilisée pour la lecture de l'heure ; dans ce cas le nom usuel est « style droit »[4] ;
- dans les grandes méridiennes, le terme « gnomon » est toujours employé. Il désigne l'élément qui laisse passer les rayons du Soleil. C'est, le plus souvent, un trou cylindrique pratiqué dans une plaque scellée en hauteur dans un mur, une verrière d'un local recevant la ligne méridienne. L'usage a donné le nom de « gnomon » à certaines méridiennes astronomiques, tel le « gnomon de Saint-Sulpice », à Paris.
-
Un gnomon du VIIIe siècle, en Chine.
-
Cadran antique à gnomon ici horizontal.
-
Cadran moderne à style polaire.
-
Cadran moderne à style droit.
-
Gnomon, élément de méridienne[5].
Description[modifier | modifier le code]
Dans sa forme la plus simple, il est constitué d'une tige fichée verticalement dans le sol. Cette tige peut avoir n'importe quelle forme ; fonctionnellement, seule compte son extrémité haute et son pied, projection verticale de cette extrémité sur la table de lecture.
- Le gnomon
- l'extrémité : l'image du Soleil n'étant pas ponctuelle, la projection de l'extrémité du gnomon s'entoure d'une pénombre qui rend son repérage difficile pour un instrument de grande taille. Aussi, plusieurs améliorations ont été apportées : extrémité à forme conique ou pyramidale facilitant le pointage par tracé des enveloppes des ombres de la pointe ; mise en place, toujours à l'extrémité, d'une sphère (boule) dont la projection enveloppe facilitera la recherche de son centre confondu avec le point recherché ; remplacement de la pointe du gnomon par un petit trou percé dans une plaque, appelé alors œilleton, et, plus tard, parfois, adaptation d'une lentille concentrant les rayons solaires[6] ;
- le pied : réel ou virtuel, il donne la hauteur du gnomon et sert de point origine dans la mesure de la longueur de l'ombre projetée sur une table de lecture[7].
- La table de lecture
Elle reçoit l'ombre portée du gnomon ; mais ce n'en est pas un élément ! À l'origine, c'était le plan du sol horizontal passant par son pied qui était utilisé. Sur les premiers cadrans solaires, cette table aura des formes multiples : hémisphérique, sphérique, conique, cylindrique, plan, etc.[8].
-
Ombre et pénombre à l'extrémité d'un gnomon cylindrique.
-
Extrémité à forme conique.
-
Extrémité en pointe et à boule.
-
Extrémité à œilleton percé dans une plaque.
-
« Gnomon »[N 1] moderne, extrémité à boule et pied virtuel.
Ombre de gnomon, faux ami[modifier | modifier le code]
Attention ! la direction de l'ombre de la tige du gnomon vertical n'indique pas l'heure[N 2]… C'est une interprétation fallacieuse de l'usage de l'instrument.
Ainsi, par un simple exemple, avec un gnomon implanté à une latitude d'environ 48° N, on s'aperçoit que pour une seule heure équinoxiale (ici celle de 8 h ou 16 h), la variation angulaire atteint 35° en fonction des saisons.

Afin que le gnomon puisse faire office de cadran solaire utilisable sur l'année, un correctif partiel peut être apporté en décalant le point de convergence des lignes horaires. Celui-ci se situera sur la méridienne du gnomon, au sud de sa base, et à une distance D= H : tg.α, H étant la hauteur du sommet du gnomon et α la latitude du lieu en question. Le cadran solaire de la place de la Concorde à Paris a été tracé en ayant recours à ce correctif[9].
Traces gnomoniques[modifier | modifier le code]
Sur une table hémisphérique[modifier | modifier le code]

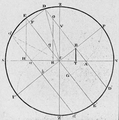
L'axe de la table étant vertical, un gnomon planté en son centre bas va projeter, comme précédemment, son ombre sur la table hémisphérique ; l'ensemble porte le nom de polos ou scaphé.
Pour un jour quelconque de l'année, à son lever, le Soleil est dans le plan horizontal. Son ombre est localisée sur le pourtour de la table (entre les limites des traces des solstices) ; puis, dans l'avancement de la journée, la course du Soleil étant continue, son ombre se déplace régulièrement jusqu'au soir[N 3], en passant sur la méridienne à midi.
Il est alors facile de diviser chaque arc diurne en 12 parties égales qui serviront de repérage horaire. Dans l'Antiquité, cette division du jour, entre le lever et le coucher du Soleil, quelle que soit la saison, correspondait aux heures temporaires[10], celles-ci ayant une durée variable qui oscillait (autour du 45e degré de latitude), entre 40 min aux solstices d'hiver (jours d'environ 8 h) et 80 min aux solstices d'été (jours d'environ 16 h) en passant par 60 min lors des équinoxes (jours de 12 h)[11].
Approche mathématique élémentaire[modifier | modifier le code]
Dans un système de coordonnées horizontales, le gnomon sert à établir la hauteur (angulaire) et accessoirement l'azimut du Soleil.
Hauteur du Soleil[modifier | modifier le code]
C'est là, l'utilisation fondamentale et originelle du gnomon.

Soit g la hauteur physique du gnomon et r la longueur de l'ombre projetée entre son extrémité et le pied du gnomon, la hauteur du Soleil sera donnée par :
Des formules simples de gnomonique[N 4] s'appliquent aux projections fondamentales de l'ombre sur la ligne méridienne, à partir de :
- La hauteur théorique du Soleil[N 5], qui à midi, est de la forme :
où φ est la latitude du lieu et δ la déclinaison du Soleil dans son mouvement annuel[N 6].
- Aux solstices, elle prend les valeurs suivantes :
où ε est l'obliquité de l'écliptique de l'époque considérée. Cette dernière est aussi la déclinaison δ maximale du Soleil.
- Aux équinoxes, où δ = 0, on aura :

À partir de ces formules[13], on peut construire une méridienne ou déterminer, en fonction de relevés expérimentaux, les solstices, les équinoxes ou d'autres indications astronomiques concernant le Soleil, telles la durée de l'année, la latitude, l'obliquité de l'écliptique, etc.
Azimut du Soleil[modifier | modifier le code]
L'azimut du Soleil A est compté positivement depuis le méridien Sud vers l'Ouest de 0° à 180° et négativement vers l'Est de 0° à -180°[14]. L'ombre du gnomon projetée sur un plan horizontal donne A compté depuis le méridien Nord par symétrie. Cet angle se mesure directement à partir de la droite méridienne. Pour une hauteur du Soleil donnée, des formules de gnomonique permettent de calculer l'azimut correspondant ; elles ne seront pas données ici, l'azimut seul ne permettant pas de tracer des lignes horaires, comme on a pu le voir précédemment.
Lignes horaires[modifier | modifier le code]
Les lignes horaires, temporaires ou équinoxiales, déduites du gnomon, ont un tracé complexe, qui n'est pas abordé ici (voir le principe du tracé dans l'article Analemme (antique). Des ouvrages de gnomonique développent le sujet[15].
Soulignons simplement que, contrairement aux idées reçues, leurs tracés supposés être un faisceau de droites dites convergentes ne passent pas par le pied du gnomon. Voir l'exemple ci-dessous pour un tracé d'heures temporaires sur un cadran antique horizontal.

Histoire[modifier | modifier le code]
Aux origines[modifier | modifier le code]
Les premiers indicateurs solaires[modifier | modifier le code]
Ils concernaient les observateurs eux-mêmes qui pouvaient être assimilés à un gnomon primitif : l'œil visant le Soleil étant l'extrémité du « gnomon » et les pieds étant le repère fixe au sol. En tournant le dos à l'aveuglant astre du jour, l'ombre de l'observateur correspondait à la direction opposée visée à l'œil. Ces deux types d'observations, directe et indirecte, ont vraisemblablement coexisté depuis des temps immémoriaux dans différentes structures sociétales réparties à travers la planète. Pour des observations répétitives, le remplacement de l'opérateur par un repère vertical fixe, un gnomon, a probablement été une évidence.
Ainsi, par la simple observation, directement ou indirectement, avec ou sans gnomon, des éléments astronomiques du Soleil ont pu être repérés au sol comme les directions de points cardinaux et celles des levers et couchers extrêmes annuels de l'astre du jour. Quelques exemples, à prendre avec prudence, illustreront ces premières applications des « gnomons » :
- Dans des tombes de Néandertaliens, les corps sont disposés suivant la direction Est-Ouest[16].
- Stonehenge (vers -3000 à -1000) et d'autres monuments mégalithiques du néolithique ont possiblement quelques pierres levées aux destinées astronomiques[17] ;

- les pyramides de Gizeh (vers -2500) ont fait couler beaucoup d'encre sur leur orientation. Une hypothèse actuelle suppose que c'est par des relevés des levers et couchers du Soleil - directions sacrées égyptiennes -, que les géomètres de l'époque ont pu tracer au sol la ligne moyenne Est-Ouest et ériger sur ces bases leurs grands monuments funéraires ;
- en Chine, un ancien palais de la période des Xia (vers -1600), est axé sur les points cardinaux, tout comme la Cité interdite de Pékin. La cosmologie chinoise conservera cette disposition géographique tout au long de son histoire impériale[18] ;
- des études contemporaines sur des peuplades à civilisation archaïque ont montré que ces hommes savaient orienter leurs constructions et même mesurer l'ombre d'un poteau en bois au solstice d'été[19].
Les premiers témoins archéologiques sur les indicateurs solaires sont égyptiens (vers -1500 à -1000). Il s'agit de règles en L graduées, avec un talon faisant office de gnomon. L'observation de l'ombre solaire avec cet instrument permet d'indiquer des instants privilégiés de la journée ou des plages temporelles qui sont qualifiées d' « heures archaïques ».

Les premiers gnomons, en Chine[modifier | modifier le code]

Les premiers grands gnomons opérationnels - à partir desquels des relevés de mesures ont été effectués - sont apparus en Chine, probablement au deuxième millénaire avant notre ère[20].
Selon la tradition, le premier calendrier chinois fut créé par l'Empereur jaune en 2637 avant notre ère, mais ce n'est qu'en -841 que l'on a des indications calendaires précises où le premier mois de l'année commence vers le solstice d'hiver. La détermination « exacte » du jour de l'hiver nécessite un gnomon, ce qui donne une plage de plus d'un millénaire pour l'apparition officielle du gnomon. C'est pendant cette période, sous la dynastie Xia, que sont mentionnés les deux astronomes légendaires Xi et He (XXIIe siècle av. J.-C. ?) illustrés ici en train d'examiner l'ombre solsticiale d'été d'un gnomon.
Les premiers gnomons astronomiques reconnus, de huit à dix pieds de hauteur (de 1,6 m à deux mètres ou plus)[N 7], ont permis des relevés de longueurs d'ombres solsticiales qui ont été conservés, ceci dès les années -1100. Rapportées en Europe au XVIIIe siècle par le Père Gaubil (Jésuite), six de ces observations, choisies pour leur précision et leur haute antiquité ont été intégrées dans une base de données qui a permis à Laplace de démontrer la diminution de l'obliquité de l'écliptique[21].
Dans le monde méditerranéen[modifier | modifier le code]
À Babylone[modifier | modifier le code]
Un passage bien connu d'Hérodote (vers 484 à 420 av. J.-C.), affirme que l'origine des instruments solaires mesurant le temps se trouve à Babylone :
« Car, pour l'usage du polos, du gnomon, et pour la division du jour en douze parties, c'est des Babyloniens que les Grecs l'apprirent[22]. »
C'est effectivement chez les Babyloniens, probablement à la fin du deuxième millénaire avant notre ère, que l'on trouve les premières informations, concernant l'usage du gnomon et plus tard du « polos »[23]. Les renseignements sur le gnomon sont extraits de tablettes cunéiformes exploitées au XXe siècle, le Mul Apin.
Le MUL.APIN, daté de -686, compile des observations astronomiques pouvant remonter à -1370. Parmi elles, on trouve une liste (non donnée) de longueurs d'ombre de gnomon, à différentes heures du jour, pour quatre jours de l'année, aux équinoxes et aux solstices[24].
On peut déjà souligner, à travers ces informations, que le gnomon est utilisé, que solstices et équinoxes sont évoqués et que des heures sont citées ; on remarquera aussi que :
- un gnomon et une ligne méridienne peuvent donner des longueurs d'ombre aux solstices et aux équinoxes, mais pas à différentes heures du jour, sans un repérage temps donné par une clepsydre adéquat ou par le polos, deux instruments connus - mais non décrits - des Babyloniens ;
- dans le texte de A. Szabo et E. Maula, il est précisé que les indications concernant la longueur de l'ombre équinoxiale sont étonnamment inexactes. Des études modernes[25] ont montré que les Babyloniens appréciaient bien le solstice d'été mais mal le solstice d'hiver (année de 360 jours et pénombre, phénomène récurrent), et ne savaient pas déterminer les équinoxes : sur la ligne méridienne, ils divisaient l'intervalle entre les solstices en deux parties égales, ce qui, évidemment, ne peut pas donner le résultat escompté[26],[N 8].

En résumé, dans l'usage du gnomon, on peut dire que les Babyloniens savaient s'en servir correctement pour repérer le solstice d'été, mais moins bien pour le solstice d'hiver et qu'ils n'appréhendaient pas les équinoxes. Ce n'est qu'un peu plus tard, chez les Grecs, que sera découverte la méthode permettant de mesurer l'ombre méridienne équinoxiale.
Chez les Grecs[modifier | modifier le code]

- Anaximandre
Au XXIe siècle, la communauté scientifique, s'appuyant sur Diogène Laërce, Eusèbe et la Souda, s'accorde pour attribuer à Anaximandre de Milet (VIe siècle avant notre ère) la découverte de la mesure fondamentale opérée avec le gnomon[27] : la détermination des équinoxes à partir des solstices[28].
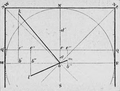
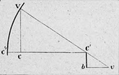
Anaximandre va s'apercevoir que les équinoxes correspondent à la bissection de l'angle TAR[N 9] défini par les droites passant par les points solsticiaux sur la méridienne et l'extrémité du gnomon.

Comment est-il parvenu à cette conclusion ? Plusieurs hypothèses sont possibles :
- en recherchant l'égalité du temps du jour et de la nuit à l'aide de la clepsydre ;
- en pointant au sol, sur la méridienne, les longueurs de l'ombre à midi, pour tous les jours compris entre les solstices. Le jour des équinoxes sera le jour médian de la demi-année définie par les solstices[N 10]. Pour ce faire, la structure du gnomon doit être assez grande, du type héliotrope ;
- en traçant au sol les arcs diurnes (voir la figure des traces gnomoniques) et en constatant que l'inversion de ces courbes passe par une droite centrale, la droite des équinoxes[N 11] ;
- par un procédé géométrique visualisant les positions solsticiales méridiennes du Soleil sur la voute céleste, associées à la représentation du gnomon et de sa méridienne. C'est la proposition que font A. Szabo et E. Maula, en s'appuyant sur la tradition, dans leur ouvrage[29].

L'association entre ces trois méthodes est de l'ordre du vraisemblable.
« Anaximandre a certainement été l'initiateur de la « représentation gnomonique du monde » qui s'est révélée indispensable au développement ultérieur de cet instrument scientifique »[30].
- L'héliotrope
Dès cette époque, comme on vient de le voir, sont installés des héliotropes - des « indicateurs de conversions [aux solstices] du Soleil » - dont on ne sait pratiquement rien. Leurs dimensions étaient censées donner plus de précision aux mesures sur la longueur de l'année et ils étaient probablement considérés comme œuvres de prestige.
Le premier de ces héliotropes est une colonne mythique évoquée par Homère (VIIIe siècle av. J.-C.) dans l'Odyssée et implantée sur l'île fabuleuse de Syrie (Syros ?). L'époque où vécut Homère montre que ces instruments ont une origine très ancienne.
Plus près de nous, on peut citer leur implantation au VIe siècle av. J.-C. à Sparte par Anaximandre ou Anaximène ; dans l'île de Syros par Phérécyde ; à Athènes, en -433, par Méton ; à Thèbes et à Syracuse, ce dernier étant « un immense héliotrope visible de loin », installé par Denys et daté du début du IVe siècle av. J.-C.[31].
- Développement de l'usage du gnomon
La connaissance des points d'équinoxes relevés sur les héliotropes va permettre, dans les siècles suivant Anaximandre, de définir un certain nombre d'informations sur l'astronomie solaire et la géographie, notamment l'obliquité de l'écliptique et la latitude du lieu où se trouve implanté le gnomon :
- Œnopide de Chios, (milieu du Ve siècle av. J.-C.), va fixer la valeur de l'obliquité de l'écliptique correspondant à la bissection de l'arc intersolsticial défini par Anaximandre. Cette bissection donne un arc de valeur constante, quel que soit le lieu d'implantation du gnomon. Œnopide va fixer cet arc et son angle, l'obliquité, à 24°, angle au centre du pentadécagone, polygone à quinze côtés, inscrit dans le cercle méridien du gnomon. Cette valeur de l'obliquité de l'écliptique, 24° sera d'usage pendant plusieurs siècles ;
- Eudoxe, (-408, -355), a peut-être utilisé une nouvelle découverte concernant la « représentation gnomonique du monde », la latitude (appelée climat dans l'Antiquité). La division du cercle en 360° étant supposée non acquise à l'époque, la latitude s'exprime par le rapport de la longueur du gnomon à son ombre ; ainsi, par exemple « En Grèce, la longueur du gnomon est à celle de l'ombre équinoxiale comme 4 est à 3[32]. », ce qui, en termes d'aujourd'hui, donne cotang φ = 4 / 3, ou plus simplement tan φ = 3 / 4 soit une latitude grossièrement égale à 37°[N 12],[33]. Concernant la durée de l'année, d'après Pline, Eudoxe aurait rapporté d'Égypte l'année de 365 jours 1/4 qu'il aurait vérifiée [sur 4 ans, au gnomon ?] à partir du solstice d'été du 13 juillet 381 av. J.-C.[34] !
- Pythéas, (probablement actif avant l'an -330), le célèbre explorateur des contrées nordiques est né dans l'antique Marseille dont il détermina la latitude avec beaucoup d'exactitude, le jour du solstice d'été. Le rapport gnomonique en ce jour de solstice était de 120 / (42 - 1/5), ce qui donne, tous calculs faits, une latitude d'environ 43° 15', très proche de la latitude actuelle du vieux port donnée par l'IGN, 43° 18'[35]. Ce relevé est la preuve que, dès le IVe siècle, le gnomon était utilisé pour déterminer la distance d'un lieu à l'équateur, autrement dit la latitude[36] ;
- Aristarque, (vers -310, -230), le père de l'héliocentrisme, a observé les solstices d'été de 280 et de 264 avant J.-C. et a essayé de déterminer, à l'heure près, l'instant du solstice de l'an 280[N 13]. Aristarque serait aussi l'inventeur du scaphé et d'un autre cadran, le « disque-plan » dont on ne sait rien[37] ;
- Ératosthène (-276, -195), a d'une part mesuré précisément l'obliquité de l'écliptique en 225 av. J.-C. D'après Delambre[38], ce serait à l'aide d'un gnomon, en effectuant une mesure de la hauteur du Soleil au solstice d'été et une autre au solstice d'hiver. La différence d'angle entre les deux mesures représente le double de l'obliquité de l'écliptique et élimine l'erreur due au demi-diamètre apparent du Soleil. Ératosthène trouvera ainsi un obliquité de 23°51'19,5", qui arrondie à 23°51'20" sera la valeur employée, plus tard, par Hipparque et par Ptolémée. L'erreur calculée aujourd'hui, par rapport à l'obliquité vraie de l'époque n'est que de 8'[39]. D'autre part, Ératosthène a déterminé la longueur de la circonférence terrestre. Cette opération de « géodésie », menée entre Alexandrie et Syène est détaillée dans la Mesure de la circonférence de la Terre. L'instrument employé à Alexandrie est supposé être un gnomon, hypothèse raisonnée de Delambre et reprise et commentée par Raymond D'Hollander[40]. C'est là, la plus célèbre utilisation du gnomon dans l'Antiquité ;
- Hipparque (-160, -120), n'utilise guère le gnomon, ayant à sa disposition divers instruments divisés en degrés - ceci depuis au-moins Ératosthène. Néanmoins, il signale, d'une part, des tables d'ombre utilisées avant lui, donnant la longueur de l'ombre du gnomon (de 6 pieds), à midi, à diverses époques de l'année exprimées en durées du jour en heures équinoxiales (voir ci-dessous) ; d'autre part il reprend, vérifie des rapports de gnomon (rapport entre la longueur du gnomon g et la longueur de l'ombre r aux équinoxes) déterminés par ses prédécesseurs[41] pour les exploiter dans la construction de sa carte dite Carte d'Hipparque[42].
| Durée du jour | 9 h | 10 h | 11 h | 12 h | 13 h | 14 h | 15 h |
|---|---|---|---|---|---|---|---|
| Longueur de l'ombre r en pieds | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| Rapport actuel du gnomon g/r | 0,75 | 0,85 | 1 | 1,2 | 1,5 | 2 | 3 |

- Ptolémée (ca. 90 - 168), comme Hipparque, n'utilisera pas le gnomon sous la forme décrite ici (voir une de ses applications à propos du quadrant astronomique). Par contre il calculera et rédigera de nombreuses tables où apparaissent des éléments gnomoniques, soit dans l’Almageste, soit dans l’Analemme[N 14]. Dans l’Almageste (Livre II, chapitre 6) il donne les caractéristiques de 39 climats (voir extrait ci-dessous) où sont indiqués la durée du jour solsticial d'été M en heures équinoxiales, la latitude φ, les longueurs d'ombre méridienne ou retrait d'un gnomon de 60 parties : re au solstice d'été, ro aux équinoxes, rh au solstice d'hiver[43] ; les valeurs des retraits sont subdivisées en sexagésimal.
| Climat | Localité | M | φ | re | r o | r h |
|---|---|---|---|---|---|---|
| Équateur | 12 h | 0° | 26p30'S | 00p | 26p30'N | |
| I | Méroë | 13 | 16° 27' | 07p45'S | 17p45' | 51p |
| II | Syène (Assouan au tropique) | 13 1/2 | 23° 51' | 00p | 26p30' | 65p50' |
| III | Basse Égypte (Alexandrie) | 14 | 30° 22' | 06p50' | 35p5' | 83p05' |
| IV | Rhodes | 14 1/2 | 36° | 12p55' | 43p50' | 103p20' |
| V | Hellespont (Rome) | 15 | 40° 56' | 18p30' | 52p10' | 127p50' |
| VI | Mi-Pont-Euxin (mer Noire) | 15 1/2 | 45° 1' | 23p15' | 60p | 155p05' |
| VII | Bouches Borysthène (Dniepr) | 16 | 48° 32' | 27p30' | 67p50' | 188p35' |
À Rome[modifier | modifier le code]
Rome ne compte guère de savants astronomes parmi ses citoyens. Le gnomon n'a pas été d'un usage remarquable. On se doit néanmoins de signaler deux « évènements » particuliers :
- la description d'une méthode pour construire toutes sortes d'horologia, c'est le fait de Vitruve ;
- la mise en place d'un célèbre gnomon, à Rome, pour vérifier un nouveau calendrier, l'horologium d'Auguste. Cet instrument scientifique existe toujours, il est érigé aujourd'hui sur une place de la ville éternelle.
- Vitruve (Ier siècle av. J.-C.)
Cet architecte de profession, est l’auteur d’un célèbre traité nommé De architectura. Au chapitre VIII du livre IX, Vitruve y décrit, dans le détail, une construction géométrique, l'analemme, employée en gnomonique. Cette méthode permet de déterminer graphiquement certains éléments des horloges solaires, c'est-à-dire des méridiennes et/ou cadrans solaires[45].
Cette construction géométrique, déjà connue avant Vitruve, est le développement de la « représentation gnomonique du monde » vue précédemment. Après l'exposé de la méthode qui s'applique en fait simplement aux méridiennes, Vitruve ne développe pas plus son sujet « par crainte d'être trop long & ennuyeux… ». La méthode de l'analemme de Vitruve sera encore employée au XVIIe siècle par Jean-Domonique Cassini dans le tracé de la méridienne de Bologne.


Au début du Ier siècle av. J.-C., les Romains avaient des difficultés avec leur calendrier qui comportait 366,25 jours. Depuis Hipparque, il était connu que l'année tropique comportait 365,2466 jours[N 15]. Sur ces bases[46], l'an 46 av. J.-C. va voir la mise en place par Jules César, du calendrier julien, dont la durée de l'année a été fixée à 365,25 jours après consultation de l'astronome Sosigène d'Alexandrie. Ce nouveau calendrier aura de la difficulté à être mis en application.
Il semble que ce soit pour mettre en évidence la longueur de l'année qu'un obélisque égyptien, haut de plus d'une vingtaine de mètres, installé au Champ de Mars est alors transformé en gnomon en l'an 10 av. J.-C., sous l'empereur Auguste ; il portera alors le nom d'« horologium d'Auguste ». Le terme « horologium » est ambigu : était-ce une simple méridienne ou un cadran solaire ? Beaucoup y voyaient un immense cadran horizontal.

Des fouilles récentes ont mis au jour des vestiges d'une simple ligne méridienne avec des incrustations transversales correspondant aux marques journalières méridiennes. Leur fonction était-elle de repérer au sol sur plusieurs années les dérives du Soleil par rapport au calendrier (ou vice-versa)[47] ?
Manilius ou Ménélaüs sont dits être, pour certains, les personnages qui ont « transformé l'obélisque en gnomon, en ajoutant au sommet une boule dorée, de sorte que l'ombre du centre de la boule corresponde sensiblement au centre du Soleil et qu'il ne soit pas nécessaire de faire la correction d'un demi-diamètre apparent du Soleil, pour avoir la hauteur méridienne du centre de celui-ci[48]. » ; pour d'autres, il s'agirait du mathématicien Facundus Novus[49].
L'œilleton, autre méthode - plus efficace d'ailleurs - pour pallier la pénombre ne sera mis en application que plus tard, au Ve siècle ou peut-être avant, par les astronomes byzantins, ou par les Arabes, suivant différentes sources[50]. En contradiction avec ces hypothèses, on peut signaler dans les cadrans antiques, le scaphé de Carthage[51], supposé être du Ier siècle, qui comporte un œilleton percé directement dans le corps du cadran.
La fonction de l'horologium d'Auguste est toujours en discussion, les avis des spécialistes sont partagés, encore aujourd'hui[52]. L'obélisque qui a servi de gnomon a été préservé. En ce début du XXIe siècle, il orne sous le nom d'Obélisque du Montecitorio la place éponyme, siège du parlement italien.
Les cadrans antiques[modifier | modifier le code]
L'Antiquité va voir l'apparition et l'expansion importante des cadrans solaires dans l'espace public et la sphère privée.
Il est rappelé que le cadran, à l'origine, est constitué d'un gnomon dont l'ombre se projette sur une table recevant des lignes horaires. Les heures tracées sur différents supports sont les heures temporaires ; on trouve aussi sur ces tables les indicateurs de saisons : les arcs diurnes.
Une étude récente sur les cadrans antiques traite de leur histoire et inventorie, dans le mobilier archéologique, plus de 600 cadrans, distribués dans 23 types différents[53].
C'est là, à travers la profusion de ses différents modèles, que l'on constate l'application « grand public » du gnomon.
- Quelques types de cadrans d'heures temporaires
-
Cadran hémisphérique de Neuss.
-
Cadran sphérique tronqué de Batna.
-
Cadran plan horizontal de Pompei.
-
Cadrans verticaux sur la célèbre tour des Vents.
-
Scaphé de Carthage (Ier siècle supposé).
Les tables d'ombre[modifier | modifier le code]
Ce sont des tables « grand public », en usage dans l'Antiquité jusqu'à la période byzantine. Elles donnent la longueur de l'ombre en fonction de l'heure et de la date. L'opérateur fait office de gnomon. Ces tables sont peu exactes : d'une part elles sont rarement précisées en latitude et d'autre part les valeurs indiquées sont arrondies et souvent en progression n'ayant qu'un lointain rapport avec la longueur des ombres portées ; mais cela avait-il de l'importance pour l'usage de tous les jours ?

Vers les grandes méridiennes[modifier | modifier le code]
Les grands gnomons, les héliotropes, permettant de mesurer précisément l'obliquité de l'écliptique se transformeront en quadrants astronomiques géants au Moyen Âge, et plus tard, à la Renaissance en méridiennes astronomiques.
En Inde[modifier | modifier le code]
Le Surya Siddhanta[modifier | modifier le code]
L'usage du gnomon est formalisé en Inde dès le IV-Ve siècle. Un important traité d’astronomie traditionnel indien, le Surya Siddhanta[N 16],[54] y consacre un chapitre entier. C'est à partir d'une version médiévale que nous sont connues les différentes applications du gnomon ; la datation des écrits - et notamment la trigonométrie employée - est donc à considérer avec prudence.
Le tracé du « cercle indien », les applications et les différents usages du gnomon sont détaillés sur 55 pages dans le chapitre III, sous forme de versets numérotés de 1 à 51[55]. Y sont développés ainsi le tracé de la méridienne, les points cardinaux, la droite d'équinoxe, la détermination de la latitude, la déclinaison du Soleil, etc. L'emploi de la trignométrie est d'usage. Certaines figures, proposées par Burgess, le traducteur du texte, sont à rapprocher de l'analemme antique[56].
- Quelques illustrations dues à Burgess
-
Le « cercle indien » et la droite d'équinoxe Q'Q.
-
Hauteur du Soleil et gnomon.
-
Comme l'analemme de Vitruve.
-
Autre construction.
« Tous les traités d'astronomie hindous postérieurs au Sûrya-Siddhânta, auront pour objet de développer et d'appliquer les préceptes contenus dans ce livre sacré[57]. ». Le gnomon sera d'un usage banal et courant, des siècles durant, notamment en architecture pour déterminer l'orientation de certains sites.
Les Rama Yantra[modifier | modifier le code]
Au XVIIIe siècle, un maharaja, Jai Singh II, fait construire cinq observatoires à l'ancienne - soit sans télescopes ni lunettes astronomiques - avec de nombreux instruments gnomoniques de tous types aux dimensions démesurées. La finalité de ces instruments étant, semble-t-il, d'améliorer les tables astronomiques existantes. Parmi eux des « gnomons très élaborés, sortes d'avatars esthétiques. ». Ces gnomons particuliers, les Rama Yantra[58], se trouvent dans l'observatoire de Jaipur, le Yantra Mandir, et celui de New Delhi, le Jantar Mantar.
Ce sont des sortes de monuments qui, pour un même site vont deux par deux, pour donner des indications complètes sur la course du Soleil. Au centre de chaque construction, un gnomon de grandes dimensions dressé verticalement. Les gnomons de Jaipur font 3,5 m de haut pour un diamètre de 8 cm. L'ombre est projetée sur deux tables complémentaires : une verticale et cylindrique qui permet de mesurer les hauteurs les plus grandes de l'ombre et une dans le plan horizontal pour les azimuts essentiellement.
Le mur cylindrique de 3,5 m de rayon est ajouré pour laisser passer vers le centre les observateurs. Le découpage est constitué de 12 secteurs gravés de 12° séparés par des « portes » de 18° ; le plan horizontal est découpé lui aussi suivant la même configuration, d'où la nécessité d'un deuxième monument complémentaire : ces « frères siamois » permettent ainsi de recevoir et mesurer toutes les ombres du Soleil, au cours de l'année[59].
-
Un Rama Yantra, vue extérieure.
-
Le gnomon et sa table cylindrique.
-
La table horizontale, au centre le gnomon[60].
Dans le monde arabo-islamique[modifier | modifier le code]
Dans le domaine astronomique, les Arabes sont les héritiers des Perses, des Indiens et surtout des Grecs. C'est sous l'impulsion du calife abbasside al-Mansûr, au VIIIe siècle que se développa la traduction et l'exploitation des connaissances extérieures, notamment l'Almageste de Ptolémée ; ceci en parallèle avec l'émergence des premiers outils trigonométriques[N 17], avec Habash[61].
- Utilisation scientifique du gnomon
Au IXe siècle, va se développer la pratique savante de l'observation et de la mesure. À la demande du calife abbasside Al-Ma’mūn, une équipe d'astronomes d'État va vérifier et préciser tous les paramètres hérités des Grecs, avec, en ce qui concerne le gnomon et ses applications, la détermination de l'inclinaison de l'écliptique, la grandeur de la Terre liée aux latitudes, etc[62]…
En 827, une équipe d'astronomes, menée par le célèbre mathématicien Al-Khwarizmi, va mesurer un arc de méridien de 2° (environ 220 km), dans la plaine du Sinjar, près de Bagdad. La distance est mesurée avec des perches, dans une direction nord-sud donnée probablement par le gnomon. Deux mesures sont effectuées indépendamment l'une de l'autre et leur écart était de 1/76e de degré, soit approximativement 1,5 km. Le procédé de mesure des latitudes initiale et finale du parcours n'est pas connu, il est probable que ce soit aussi au gnomon ; l'obliquité par différence solsticiales est donnée pour 23° 33' (vers l'an 1000 ce sera plutôt 23° 35'). Le résultat final donnera 111,8 ± 1,5 km au degré (à comparer à la valeur d'aujourd'hui qui est de 111,3 km)[63].
-
Al-Khwarizmi, célèbre mathématicien (vers 780 - 850).
-
Cours du Nil, par Al-Khwarizmi (manuscrit de 1036-1037).
-
Climats et latitudes donnés par les Arabes, au XIIIe siècle.
- Le cadran solaire

L'intérêt des Arabes pour cet indicateur solaire est considérable ; ce sera un de leurs instruments privilégié. L'astronome Thābit ibn Qurra[56], au IXe siècle, décrira la construction de cadrans solaires aussi bien en heures temporaires qu'équinoxiales. Pour les besoins religieux, la détermination des heures de prière et la direction de La Mecque sont des fondamentaux. Après tâtonnements, ces déterminations seront effectives au XIe siècle[64]. Sur les cadrans, des gnomons spécialisés seront implantés et dédiés à cet effet. Il arrive que, par cadran, l'on trouve jusqu'à cinq gnomons, chacun ayant une fonction particulière ; ces gnomons sont reconnaissables à leur forme trapue et pyramidale. Il faut souligner aussi la mise en usage, au XIIIe siècle, du style polaire pour indiquer les heures équinoxiales (Voir le cadran de la Mosquée Umayyade à Damas). Les ouvrages d'Aboul-Hhassan, de cette époque sont une source inépuisable d'informations[65].
En Chine[modifier | modifier le code]

Depuis les dynasties des Han de l'Ouest (-205 à -8) et de l'Est (-25 à 220), l'usage du gnomon est bien documenté à travers les écrits du père Gaubil étudiés par Biot[66].
Dès cette époque et même avant, d'après un recueil chinois, le Tcheou-Pey, l'année solaire comprise entre deux retours du Soleil au même solstice - donc mesurée au gnomon - est de 365,25 jours[N 18] ; l'obliquité de l'écliptique est donnée pour 24° chinois, qui ne font pas 23°40'[67]. Dans les années -1100, le gnomon a une hauteur officielle de 8 pieds chinois (environ 1,6 m) et il a été muni d'un œilleton pendant une courte période. Cet usage, qui a fait long feu, ne se retrouvera plus que sous forme de sténopé dans les années 1275.
Toujours sous les Han, l'ombre méridienne du gnomon est utilisée pour définir des distances entre villes éloignées en latitude. Ainsi, la longueur de l'ombre [équinoxiale ?] était dite varier d'un pouce chinois tous les 1 000 lis (qui valaient 443 m sous les Tang). Sous la dynastie Sui (vers les années 600), cette règle en usage est mise en doute par l'astronome Liu Zhuo qui alerte l'empereur :
« … [il est souhaitable] d'ériger des gnomons pour suivre saisons, solstices et équinoxes et pour mesurer l'ombre du soleil le même jour. De la différence des ombres, la distance en lis peut être connue. ».
Ce n'est que sous l'empereur Xuanzong, dans les années 721 à 725, que des astronomes dont Yi Xing ont tracé une méridienne géodésique sur environ 2 500 km correspondant à un arc de plus de 23°. Cette expédition comportait plus d'une dizaine de stations. À chaque point retenu était érigé un gnomon pour mesurer les ombres solsticiales et la latitude. Il reste un exemplaire de ces gnomons, actuellement présenté au musée de l'ancien observatoire de Dengfeng. Haut de 8 pieds chinois - suivant la norme - ce dernier a une particularité : l'ombre solsticiale d'été est tangente à la face latérale nord du socle trapézoïdal. Après l'expédition et le dépouillement des résultats, les calculs - peut-être réalisés avec l'aide de la trigonométrie indienne - démontrèrent que la règle ancestrale d'un pouce chinois pour 1 000 lieues était erronée ; la longueur de l'ombre variait en fait d'un pouce tous les 250 lieues environ. Yi King en déduit qu'un arc de méridien de 1° correspondait à 351 et 80/300e lieues, soit 155 km - mesure honorable à comparer aux 111 km déterminés par Delambre en 1791, plus de 1 000 ans après l'expédition chinoise[68].
Plus tard, autour de 1275, un gnomon monumental ou méridienne est construit sur le site de l'ancien observatoire astronomique de Gaocheng. Il est connu sous le nom de « Tour de l'Ombre ». Le gnomon est une barre horizontale et la projection de son ombre est reçue sur une table méridienne de plus de 31 m de long. Pour éviter le flou nuisible à la lecture, un sténopé mobile permet d'obtenir une image projetée assez nette. Cet instrument hors-norme a permis de mesurer précisément la longueur de l'année.
- La Tour de l'Ombre
-
Vue de l'instrument monumental.
-
La table méridienne vue du gnomon.
-
Schéma fonctionnel[69].
D'autres gnomons, de plus petites dimensions, seront établis sous les Mings, à Gaocheng, à l'observatoire antique de Pékin ou à l'observatoire de la Montagne Pourpre près de Nankin, tel le gnomon rallongé en U et muni d'un œilleton, visible à Nankin[70].
- Autres gnomons
-
Gnomon secondaire à Dengfeng.
-
Gnomon à l'ancien observatoire de Pékin.
-
Voir à l'observatoire de la Montagne Pourpre[70].
Ce seront les derniers gnomons. Ils seront accompagnés puis remplacés par d'autres instruments, plus spécialisés que l'on peut voir notamment à l'observatoire antique de Pékin.
-
Observatoire antique de Pékin, 1737.
Époque contemporaine[modifier | modifier le code]

Le gnomon qui s'est transformé, dans son appellation, en méridienne à la Renaissance sera remplacé, petit à petit, par des instruments plus performants dans la deuxième partie du XVIIIe siècle, tel le quadrant astronomique. Néanmoins,
- il sera choisi comme emblème originel du Notariat, du temps de Louis XIV, au XVIIe siècle, mais son illustration s'est transformée en cadran solaire multifaces au cours du temps[71] ;
- dans les éphémérides de la Connaissance des temps de 1702, son usage est décrit sur 4 pages « pour trouver les latitudes ou hauteurs de pôle »[72] ;
- Dans le domaine spatial, il est utilisé par la NASA pour ses explorations. Par exemple, lors de la mission Apollo 17 sur la Lune il a été intégré pour déterminer la position des échantillons et calibrer les instruments[73]. D'autre part, en décembre 2018, une autre mission vers Mars, comprenant l'atterrisseur InSight, a utilisé un gnomon spécial comme boussole martienne[74],[75].
- Dans le domaine de l’art, Le Mont Solaire, œuvre éphémère de Land art, transforme le mont Saint-Michel en gnomon - plutôt en style de cadran solaire -, utilisant la flèche de l’abbaye durant l'équinoxe d’automne 1988. La baie devient la table horizontale et support à la droite d’équinoxe d'une longueur de 1 125 m allant de 7 h 30 min à 4 h 30 min TU. Elle est constituée de 7 chiffres romains, du IX au III, d'une vingtaine de mètres de long, ainsi que de points symbolisant les demi-heures.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- C'est en fait un style droit.
- Sauf pour l'heure de midi, ce que l'on peut voir sur la figure
- La course du Soleil sur la voûte céleste et la course de l'ombre sur la table forment une homothétie dont le centre est l'extrémité du gnomon.
- Le modèle de calcul employé en gnomonique considère la déclinaison solaire comme constante tout au long du jour ; d'autre part, ici seront négligés le diamètre du Soleil, la réfraction et d'autres facteurs secondaires.
- La formule générale de la hauteur du Soleil donnée pour information est de la forme : sin h = sin δ sin φ + cos φ cos δ cos H, où H est son angle horaire ; à midi H = 0 ; on peut en déduire la longueur de l'ombre correspondante l.
- Des tables donnent les valeurs de la déclinaison du Soleil pour tous les jours de l'année ; elles varient quelque peu en fonction de l'époque.
- La valeur du pied chinois a varié entre 20 et 30 cm au cours des époques, d'après Jean-Marc Bonnet-Bidaud 2017, p. 117.
- La détermination babylonienne des équinoxes sur une ligne méridienne permet de préciser que pour la définition des heures la clepsydre serait plus adéquat que le polos, à moins que ce dernier ne comporte pas de ligne d'équinoxes.
- Cet angle correspond à l'« arc intersolsticial », désignation proposée par A. Szabo et E. Maula.
- La méthode est intuitive, mais approximative ; les lois de Kepler le démontreront.
- L'appréhension de cette droite est temporellement difficile.
- Cette hypothèse, proposée par Szabo est incertaine, par contre une autre approche de la latitude par le rapport du jour le plus long au jour le plus court est hors de doute car rapportée par Hipparque qui reprochait à Aratos-Eudoxe de s'être trompé en donnant pour la Grèce ce rapport égal à 5 / 3 au lieu de 4 / 3.
- D'après Raymond D'Hollander 2002, p. 118, B. L. Van der Waerden a reconstitué la date d'observation d'Aristarque. Elle aurait eu lieu le 26 juin, avec le solstice donné pour 7 heures de l'après-midi. L'erreur d'appréciation (d'après Van der Waerden) d'Aristarque serait comprise entre 6 h et 12 h avant l'instant du solstice proprement dit.
- Les tables de l’Analemme sont pratiquement toutes perdues.
- Pour information, l'année tropique admise aujourd'hui est de 365,2422 jours. L'année d'Hipparque s'en différence de 0,0044 jour soit 6 min 20 s.
- Du sanscrit Surya Siddhanta, formé de Surya, « Soleil », et de Siddhanta, « doctrine certaine » ou « vérité assurée » traduit par « la solution du Soleil »
- Tables des sinus, sous l'influence indienne et aussi des tangentes, dès le IXe siècle.
- Cette division est aussi attribuée à la division de la circonférence, pour avoir la correspondance : 1 jour = 1° où le degré chinois vaut alors 0° 59' 8,25" de nos unités d'angle ; cet usage sera conservé jusqu'au milieu du XVIIe siècle.
Références[modifier | modifier le code]
- Michel Serres, « L’axe du cadran solaire », Études françaises, volume 24, numéro 2, automne 1988, p. 39-40 (lire en ligne).
- E. Benoist & H. Goelzer, Nouveau Dictionnaire latin-français, Paris, Garnier, , p. 635.
- Jérôme Bonnin 2015.
- Denis Savoie 2007.
- Voir la méridienne de l'abbaye de Saint-Pierre-sur-Dives accès en ligne.
- Pour approfondissement voir : G. Ferrari, Cadran Info Spécial 2012 : Propriétés de l'ombre, Paris, SAF, coll. « Cadran Info », , p. 14-43.
- Denis Savoie 2003, p. 40-47
- Jérôme Bonnin 2015, p. 132-144 et autres.
- https://www.elsolieltemps.com/pdf/gnomonica/213.pdf
- Delambre 1817+, p. 510-514.
- « Le gnomoniste cadranier, gardien de la mesure du temps – LE PLUMARIUM » (consulté le )
- Jean Sylvain Bailly, Histoire de l'astronomie moderne, t. 2, Paris, de Bure, (lire en ligne), p. 739
- Denis Savoie 2003, p. 41-42
- Denis Savoie 1997, p. 11.
- Voir par exemple dans Denis Savoie 2007, p. 295-297 et 131.
- Pascal Picq, Les Origines de l'homme : l'odyssée de l'espèce, Paris, Tallandier - le Seuil, 1999 - 2002, 159 p. (ISBN 978-2-84734-010-5 et 2-84734-010-6), p. 123.
- Gérald S. Hawkins, Soleil sur Stonehenge, Copernic, , dans J. P. Mohen, Les mégalithes pierres de mémoire, Gallimard, , p. 78, 148.
- Jean-Marc Bonnet-Bidaud 2017, p. 14 ; 16,17.
- Claude Lévi-Strauss, Tristes Tropiques, Paris, Plon, , p. 249 ; (it) Fred Hoyle, L'astronomia : Il camino della scienza, Sansoni, , p. 31.
- Et, peut-être même dès le troisième siècle, sous la dynastie Yin-Zhou d'après accès en ligne.
- Voir un article très documenté, aux nombreuses références, Denis Savoie 2017, p. 130-131
- Hérodote, Histoires, vol. II, Paris, Les Belles Lettres, , p. 109.
- Le « polos », cité par Hérodote vivant au Ve siècle av. J.-C., est dit avoir été inventé par Bérose, vers la fin du IVe siècle av. J.-C. d'après Vitruve cité par Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne), Livre IX, chap. VIII p. 285… ; voir aussi le texte latin et sa traduction sur le site de Philippe Remacle, Remacle, lire en ligne. Delambre le détaille sur plusieurs pages dans son ouvrage Delambre 1817+, p. 510-514.
- A. Szabo - E. Maula 1986, p. 34.
- (en) D. R. Dicks, Early Greek Astronomy to Aristotte, New York, Ithaca, , p. 166.
- A. Szabo - E. Maula 1986, p. 35.
- A. Szabo - E. Maula 1986, p. 26, 27,36.
- Voir aussi Jérôme Bonnin 2015, p. 52.
- A. Szabo - E. Maula 1986, p. 49-50.
- A. Szabo - E. Maula 1986, p. 161.
- A. Szabo - E. Maula 1986, p. 30-31 et Jérôme Bonnin 2015, p. 53.
- Rapporté d'Hipparque dans A. Szabo - E. Maula 1986, p. 17..
- A. Szabo - E. Maula 1986, p. 121-169..
- Raymond D'Hollander 2002, p. 51.
- Raymond D'Hollander 2002, p. 89.
- A. Szabo - E. Maula 1986, p. 95..
- Pour les cadrans solaires voir le texte latin et sa traduction sur le site de Philippe Remacle, Remacle, lire en ligne.
- Delambre 1817, p. 87-88.
- Raymond D'Hollander 2002, p. 128,
- Delambre 1817, p. 89-91, Raymond D'Hollander 2002, p. 128-132.
- Claude Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne), Livre IX, chap. VII-1.
- Raymond D'Hollander 2002, p. 186-187.
- Raymond D'Hollander 2002, p. 255-260.
- Ptolémée décrit, en faits, 39 climats différents ; Raymond D'Hollander 2002, p. 253, 261 ; Germaine Aujac 1993, p. 58.
- Claude Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne).
- Ptolémée, Almageste, vol. III-I.
- Jérôme Bonnin 2015, p. 295-301.
- Raymond D'Hollander 2002, p. 214 ; Delambre 1817, p. lxiij, Pline, liv. 36, chap. 10.
- Voir l'ouvrage History of the Sciences in Greco-Roman Antiquity, accès en ligne.
- Denis Savoie 2017, p. 129-130.
- Denis Savoie et Roland Lehoucq, Étude gnomonique d'un cadran solaire découvert à Carthage, vol. 25, Paris, Persée, coll. « Revue d'Archéométrie », (lire en ligne), p. 25-34.
- Jérôme Bonnin 2015, p. 302-307.
- Jérôme Bonnin 2015.
- Étymologie d'après J.-B. Biot 1862, p. 174 ; traduction, Denis Savoie 2017, p. 131.
- Voir le sommaire du chapitre III, accès en ligne
- Denis Savoie 2014, p. 91.
- J.-B. Biot 1862, p. 66
- Voir une vidéo, accès en ligne.
- Denis Savoie 2017, p. 131-132.
- Voir d'autres vues, Wikimedia Commons
- Ahmed Djebbar, Une histoire de la science arabe, Paris, Seuil, coll. « Points sciences », (ISBN 978-2-02-039549-6), p. 184-185.
- Ahmed Djebbar, L'âge d'or des sciences arabes, Paris, Le Pommier & La cité des sciences et de l'industrie, , 187 p. (ISBN 2-7465-0258-5), p. 68-75 ; 107.
- Claude Brezinski, Les images de la Terre : cosmographie, géodésie, topographie et cartographie à travers les siècles, Paris, L'Harmattan, , 300 p. (ISBN 978-2-296-11722-8, lire en ligne), p. 37 ; voir aussi Delambre 1819, p. 78, 100-101, 156.
- Denis Savoie 2014, p. XX.
- J.-J. Sédillot, Traité des instruments astronomiques des Arabes : Composé au treizième siècle par Abqul Hhassan Ali, de Maroc, t. II, Paris, Imprimerie royale, (lire en ligne), p. 388 ; Delambre 1819, p. 515.
- J.-B. Biot 1862, p. 279-280 ; 296-311
- Delambre 1819, p. xij.
- Jean-Marc Bonnet-Bidaud 2017, p. 109-117.
- Voir un site dédié
- Voir le gnomon en U à Nankin, 1446-1744.
- Voir commentaires.
- accès en ligne.
- voir une illustration sur "Les calendriers SAGA" ; voir une autre image du gnomon.
- Denis Savoie 2017, p. 135 ; voir aussi Denis Savoie, Déterminer le nord géographique martien, vol. 116, Paris, SAF, coll. « L'Astronomie », , p. 38-39. Voir aussi la page Insight et son gnomon
- Insu, « Un instrument babylonien a aidé à déterminer le Nord géographique de Mars », sur futura-sciences.com (consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- Jérôme Bonnin, La mesure du temps dans l'Antiquité, Paris, Les Belles Lettres, , 444 p. (ISBN 978-2-251-44509-0).

- Denis Savoie, Gnomonique moderne, Paris, SAF, , 252 p. (ISBN 2-901730-05-1).

- Denis Savoie, Les cadrans solaires, Paris, Belin, coll. « Pour la science », , 127 p. (ISBN 2-7011-3338-6).

- Denis Savoie, La gnomonique, Paris, Les Belles Lettres, , 521 p. (ISBN 978-2-251-42030-1).

- Denis Savoie, Recherches sur les cadrans solaires, Paris, Brepols, coll. « De diversis artibus », , 242 p. (ISBN 978-2-503-55298-9).

- Denis Savoie, Du gnomon à la méridienne, vol. 36, Paris, SAF-CCS, coll. « Cadran Info », , p. 123-135.

- Jean-Marc Bonnet-Bidaud, 4000 ans d'astronomie chinoise : Les officiers célestes, Paris, Belin, coll. « Bibliothèque scientifique », , 191 p. (ISBN 978-2-7011-3652-3).
 .
. - A. Szabo - E. Maula (trad. de l'allemand), Les débuts de l'astronomie, de la géographie et de la trigonométrie chez lzs Grecs, Paris, J. Vrin, coll. « L'histoire des sciences, textes et études », , 238 p. (ISBN 2-7116-0911-1).
 .
. - Raymond D'Hollander, Sciences géographiques dans l'antiquité : connaissance du monde, conception de l'univers, Paris, Aft et Ign, , 465 p. (ISBN 2-901264-53-0).

- Delambre, Histoire de l'astronomie ancienne, t. I, Paris, Courcier, .

- Delambre, Histoire de l'astronomie ancienne, t. II, Paris, Courcier, 1817+.

- Delambre, Histoire de l'astronomie du Moyen Âge, Paris, Courcier, (lire en ligne).

- J.-B. Biot, Études sur l'astronomie indienne et chinoise, Paris, Levy, (lire en ligne).
 .
. - Michel Serres, « L’axe du cadran solaire », Études françaises, volume 24, numéro 2, automne 1988, p. 35–51 (lire en ligne).
- Denis Savoie, « Usages astronomiques du gnomon au cours des siècles », Comptes Rendus Geoscience, vol. 350, no 8, , p. 487-497 (DOI 10.1016/j.crte.2018.08.001)
- Joseph Mollet, Gnomonique graphique, ou Méthode simple et facile pour tracer les cadrans solaires sur toute sorte de plans, en ne faisant usage que de la règle et du compas, Paris, Éd. Vve Coursier, .
Articles connexes[modifier | modifier le code]
- Méridienne (gnomonique)
- Gnomon (géométrie)
- Gnomonique
- Cadran solaire
- Anneau astronomique
- Histoire de la mesure du temps
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- « Évolution des cadrans solaires » (consulté le )
- Usages astronomiques du gnomon au cours des siècles
- Gnomon monumental du Mont Saint-Michel





![Gnomon, élément de méridienne[5].](http://upload.wikimedia.org/wikipedia/commons/thumb/7/72/Saint-Pierre-sur-Dives_%C3%A9glise_Notre-Dame_gnomon.JPG/120px-Saint-Pierre-sur-Dives_%C3%A9glise_Notre-Dame_gnomon.JPG)




![« Gnomon »[N 1] moderne, extrémité à boule et pied virtuel.](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9d/Sezimovo_copie.jpg/90px-Sezimovo_copie.jpg)









![La table horizontale, au centre le gnomon[60].](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f3/Jantar_Mantar%2C_Jaipur%2C_Rajasthan%2C_India_%28SkyDreamMW%29.jpg/120px-Jantar_Mantar%2C_Jaipur%2C_Rajasthan%2C_India_%28SkyDreamMW%29.jpg)





![Schéma fonctionnel[69].](http://upload.wikimedia.org/wikipedia/commons/thumb/8/82/Dengfeng_Observatory_schema.png/120px-Dengfeng_Observatory_schema.png)


![Voir à l'observatoire de la Montagne Pourpre[70].](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e4/Ancient_Beijing_observatory_06.jpg/120px-Ancient_Beijing_observatory_06.jpg)
