Analemme (antique)

Un analemme (en grec ancien : ἀνάλημμα, « construction qui en supporte une autre ») est une ancienne construction géométrique, employée en astronomie-gnomonique. Elle permet de déterminer principalement certains éléments fondamentaux liés au mouvement annuel du Soleil sur les horloges solaires (méridiennes et/ou cadrans solaires).
La figure de base est une représentation simplifiée de la sphère céleste, qu'on peut comparer à la sphère armillaire. C'est une projection orthographique de la sphère dans un plan, le plus fréquemment dans le plan du méridien.
Cette figure de base est ensuite exploitée dans une projection gnomonique dans les domaines suivants :
- sur une méridienne, elle va permettre de déterminer, en fonction des données initiales, les solstices, équinoxes, latitude, obliquité de l'écliptique, etc. ;
- dans le domaine des cadrans solaires, de moindre dimensions, les applications initiales sont limitées - comme sur une méridienne - au pointage des solstices et équinoxes sur la ligne horaire de midi. La détermination de tous les autres éléments : lignes d'heures temporaires et arcs diurnes, sera elle aussi possible mais guère exploitée, semble-t-il.
Dans l'Antiquité, la méthode est citée par Vitruve ; plus tard, à l'époque moderne Jean-Domonique Cassini l'utilisera dans la description du tracé de sa méridienne de Bologne avant 1695.
La méthode de Vitruve appliquée à une méridienne sera succinctement reprise par Claude Ptolémée ; il proposera aussi un ouvrage De l'analemme qui en s'appuyant au départ sur cette méthode propose une solution trigonométrique au repérage du Soleil sur la voute céleste, solution qui avait une potentielle application en gnomonique. Mais cette méthode compliquée fera long feu.
Différents ouvrages de gnomonique d'érudition reprendront et approfondiront les méthodes de l'analemme antique, et ceci jusqu'à aujourd'hui.
Analogie avec la sphère céleste[modifier | modifier le code]
L'analemme (du grec ancien ἀνάλημμα, analêmma, composé de ana- « à travers » et de lemma « proposition auxiliaire »), est une figure auxiliaire - représentation en deux dimensions de la sphère céleste -, à travers laquelle on pourra déterminer, soit graphiquement, soit par calcul trigonométrique, des éléments fondamentaux de la mécanique céleste liés à la course d'un astre (Soleil ou étoile).
La détermination de ces éléments facilitera, à la suite, la construction de figures principales plus sophistiquées en astronomie-gnomonique.
- De la sphère céleste à l'analemme
-
1 - Sphère céleste.
-
2 - Sphère armillaire (3D).
-
3 - Sphère armillaire simplifiée.
-
4 - Analemme simple (2D)
- Commentaires
- la sphère céleste est une sphère imaginaire ; on peut la représenter en trois dimensions (3D) ou en deux (2D) ;
- la sphère armillaire est la matérialisation en 3D de la sphère céleste. Elle est composée d'un grand nombre d' éléments fondamentaux ;
- la sphère armillaire peut être simplifiée si besoin ;
- l'analemme est la représentation en 2D de la sphère céleste : cet analemme peut être plus ou moins sophistiqué en fonction des besoins.
L'analemme est donc une projection sur un plan de la sphère céleste. Cette projection est dite projection orthographique. Le plan de projection peut être vertical, horizontal, etc. La projection privilégiée est une projection dans le plan du méridien local (plan vertical nord - sud) ; c'est celle qui est visualisée ici[1].
Description de l'analemme de base[modifier | modifier le code]
On y trouve les mêmes éléments que sur la sphère armillaire ; ils sont repérés ici comme sur la figure dite de Vitruve[2] donnée par Perrault :

- l'horizon du lieu EI ;
- l'axe des pôles QP ou axe de la sphère céleste, incliné sur l'horizon de la latitude φ du lieu, soit l'angle PAI ;
- l'équateur céleste NF, lieu du Soleil aux équinoxes ; le point N est donc le lieu du Soleil à midi en ces jours ;
- le tropique du Capricorne KH, lieu du Soleil au solstice d'hiver, incliné de -ε par rapport à l'équateur ; K est le lieu du Soleil à midi en ce jour ;
- le tropique du Cancer LG, lieu du Soleil au solstice d'été, incliné de ε par rapport à l'équateur ; L est le lieu du Soleil à midi en ce jour ;
- la position de l'écliptique KG au solstice d'hiver ;
- la position de l'écliptique LH au solstice d'été ;
- au centre de la sphère, en A, une boule représentant la Terre[3].
Cette représentation initiale que nous appellerons « sphère » pourra être complétée par des tracés supplémentaires, ou simplifiée, en fonction de la spécificité des applications.
Applications gnomoniques[modifier | modifier le code]
L'analemme permet de déterminer graphiquement certains éléments liés à la mécanique des astres et notamment du Soleil. Les figures employées peuvent être la base de solutions trigonométriques qui ne seront pas abordées ici.
Méridiennes[modifier | modifier le code]
Soit une méridienne horizontale supposée tracée au sol dans le plan du méridien[N 1], à partir du pied du gnomon.

Deux applications peuvent alors se présenter :
- à partir de la hauteur du gnomon et de la latitude du lieu, on veut déterminer les points solsticiaux et le point double des équinoxes ;
- la hauteur du gnomon étant connue et les points solsticiaux étant repérés sur la ligne méridienne, on cherche le point des équinoxes et la latitude.
Dans les deux cas, la hauteur du gnomon est connue. Son sommet est alors confondu avec le centre de la « sphère » en A, centre du Monde et de la Terre. La « sphère » a pour rayon la hauteur du gnomon et elle est tangente à la ligne méridienne en B ; elle peut donc être tracée avec son horizon EAI. Ensuite, suivant le cas, on procèdera différemment.
Recherche des solstices et des équinoxes[modifier | modifier le code]
Données : hauteur du gnomon et latitude du lieu.
- Tracer QP faisant l'angle PAI avec l'horizon correspondant à la latitude φ.
- Tracer la ligne des équinoxes NAF perpendiculaire à QP, la prolonger jusqu'à la ligne méridienne en C (projection gnomonique), ce sera le point remarquable des équinoxes
- Tracer symétriquement par rapport à NFC, les segments KG et LH à partir de l'angle de l'obliquité ε ; prolonger ces segments jusqu'à T et R sur la ligne méridienne (projection gnomonique). Ces points seront les points remarquables des solstices.

Recherche des équinoxes et de la latitude[modifier | modifier le code]
Données : hauteur du gnomon et points solsticiaux.
- L'analemme se trace dans l'ordre inverse du cas précédent, on en déduit le point C des équinoxes, la latitude φ du lieu et l'obliquité de l'écliptique ε[4].
Détermination de l'entrée du Soleil dans les signes zodiacaux[modifier | modifier le code]
La méthode de l'analemme peut aussi permettre le tracé sur la ligne méridienne des points correspondant à l'entrée du Soleil dans chaque signe du zodiaque.
Sur la figure de base, il suffit de rajouter un cercle de diamètre KL entre ces deux points et de le diviser en douze « mois » zodiacaux (correspondants à la longitude écliptique). Par rabattement on trouve la position du Soleil, à l'entrée de chaque mois, sur le cercle méridien (sa déclinaison). On peut alors construire, comme précédemment pour les cercles solsticiaux, la position de l'ombre du gnomon sur la ligne méridienne. Pour ne pas surcharger la figure, le cercle des « mois » a été tracé entre K et L et non entre H et G comme chez Vitruve ; la construction n'a été donnée ici que pour l'entrée du Soleil dans le signe du Taureau[5].

Détermination de la durée du jour[modifier | modifier le code]
Sur la figure de l'analemme de base appliqué à une méridienne, les segments kV, NA, LS représentent la projection de la course du Soleil au dessus de l'horizon aux jours des solstices et des équinoxes. On a donc, par là, une image de la variation de la durée du jour de lumière en fonction des saisons[7].
Par exemple, on peut le vérifier aux équinoxes où la durée du jour est égale à celle de la nuit, soit une durée de 12 heures équinoxiales ou temporaires. Ici, le Soleil se lève à l'horizon est en A, passe à midi - 6 heures plus tard - en N, puis se couche à l'horizon ouest en A, à la douzième heure. Le rabattement de l'arc semi-diurne[N 2] NP (qui est ici confondu avec le cercle de la « sphère ») permet de visualiser la position du Soleil aux différentes heures du jour espacées de 15° et de construire éventuellement sa projection sur NA : l'exemple donné ici correspond à midi ± 2 h, soit à 10 h et 14 h en heures équinoxiales ou à la quatrième et huitième heure temporaire.

- détermination de la durée du jour solsticial d'été
Le segment LS représente la projection de la course du Soleil au dessus de l'horizon au jour du solstice d'été. Le rabattement de LMG permet de situer S' sur l'arc diurne qui ici est divisé en heures équinoxiales. Graphiquement on peut donc mesurer l'arc semi-diurne LS' correspondant à la demi-durée du jour, soit ici un peu moins de 7,5 h équinoxiales pour une latitude supposée de 43° ; ce qui donnera pour la durée du jour M ≈ 14 h 56 m.

Remarques :
- la division de l'arc LS' en 6 parties donnera la longueur en degrés d'une heure temporaire ;

- la méthode employée ici peut être étendue à n'importe quelle déclinaison solaire comprise entre ± ε ou éventuellement à celle d'un autre astre de déclinaison connue[8].
Cadrans solaires[modifier | modifier le code]

La projection de « la sphère » sur le plan horizontal, à partir de sa représentation dans le plan du méridien, va permettre de définir des points appartenant aux lignes horaires temporaires d'un cadran horizontal. Une construction point à point judicieuse permettra de tracer les lignes de déclinaison ou arcs diurnes et les lignes d'heures temporaires[9].
- construction d'un point horaire du cadran
On prendra pour exemple la recherche du point correspondant à la quatrième heure temporaire au solstice d'été.
Soit l'analemme défini dans le plan du méridien, de centre A, de rayon AB qui se projette en O dans le plan horizontal, avec le point 4' sur LG correspondant à la quatrième heure temporaire[N 3] :
- la projection gnomonique de 4' (passant par A) sur la ligne de terre XY donne le point 4" et sa trace perpendiculaire à XY dans le plan horizontal, soit D4" droite où se trouveront les points 4 et 8 du cadran ;
- la projection du point 4' perpendiculairement à XY est la droite D4' sur laquelle se trouveront en projection horizontale les points 4° et 8° ;
- soit un plan auxiliaire horizontal Pa passant par 4'. Ce plan coupe la sphère suivant un cercle Ca en vue de dessus ; 4° et 8° se trouvent donc à l'intersection de Ca et de D4'. Les droites 4°O et 8°O vont couper D4" en 4 et 8, points du cadran ;
- on peut construire aussi les points 4 et 8 en se servant du point auxiliaire 4"' qui ramène 4' dans le plan du méridien. La projection gnomonique de 4"' donne le point 4"" sur XY et par là le cercle de centre O et de rayon B4"" qui coupera D4" aux points recherchés.
Ainsi on peut construire point par point, heure par heure, l'arc diurne d'été, puis l'arc diurne d'hiver et éventuellement l'arc solsticial. Les points d'une même ligne horaire temporaire sont,sous nos latitudes[Lesquelles ?], sensiblement sur une même droite.

Cette méthode de construction peut être mise en application dans un plan vertical orthogonal au plan du méridien. Elle permettra alors de construire point à point un cadran d'heures temporaires méridional. De la même façon, il peut être tracé des cadrans d'heures équinoxiales soit dans le plan horizontal, soit dans le plan vertical.
Histoire[modifier | modifier le code]
Vitruve[modifier | modifier le code]
Dans l'Antiquité, la méthode de l'analemme est décrite pour la première fois par Vitruve au Ier siècle av. J.-C. dans le chapitre Manière de faire un analème de son ouvrage De architectura traduit en français par Claude Perrault en 1684 et par J. Soubiran en 1969. La traduction du texte latin est accompagnée de commentaires explicatifs[10].
Vitruve se contente d'appliquer l'analemme à la description d'une méridienne. À la fin du chapitre VIII du livre IX, il ne développe pas plus son sujet « par crainte d'être trop long & ennuyeux… », mais l'application au tracé des heures de toutes sortes de cadrans est suggérée.
Hipparque[modifier | modifier le code]
Dans sa description de l'analemme, Vitruve qui était architecte, s'est probablement inspiré d'auteurs astronomes qui l'auraient précédé. Raymond D'Hollander, s'inspirant probablement de Neugebauer et de Vogt[11], décrit notamment les analemmes d'Hipparque (-160, -120), et pense que ces analemmes étaient peut-être connus avant même Hipparque, mais sous forme graphique seulement. Sur les analemmes d'Hipparque, D'Hollander propose[12] comment :
- déterminer la déclinaison du Soleil pour une longitude écliptique donnée (voir la figure Détermination par l'analemme de l'entrée du Soleil dans le signe du Taureau ♉ et le texte correspondant) ;
- déterminer un arc diurne, notamment la durée du jour solsticial d'été (durée du jour le plus long), et celle du jour solsticial d'hiver (durée du jour le plus court). La durée du jour solsticial d'été M a été une référence pour établir le tableau des principaux climats (voir Les sept principaux climats d'Hipparque).
Ptolémée[modifier | modifier le code]
Au IIe siècle, Claude Ptolémée reprendra succinctement l'analemme pour « trouver les rapports des gnomons à leurs ombres équinoxiales et solsticiales à midi »[13] ; en clair l'application à une méridienne avec les calculs trigonométriques correspondants[14].

Il écrira un ouvrage sur le sujet, De l'Analemme (le texte grec est fragmentaire, mais le traité nous est parvenu intégralement par une traduction latine, elle-même sans doute issue de l'arabe[15]). Jean-Baptiste Delambre donne une explication cohérente de la méthode utilisée[1].
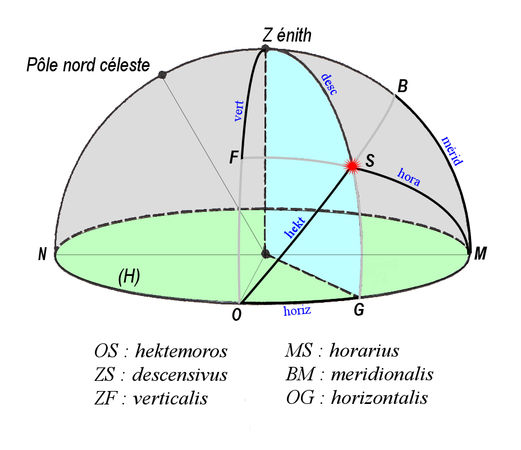
Ptolémée s'appuie sur « la sphère » pour définir et calculer par la trigonométrie six arcs-angles de grands cercles pouvant définir la position du Soleil à un moment et à une latitude donnés dans le référentiel : plan méridien, plan Est-Ouest, horizon. Ces angles aux noms antiques[N 4] sont mieux visualisés sur une représentation sphérique plutôt que sur un analemme comme le propose Delambre qui suit Ptolémée.
- L'analemme et Ptolémée
-
Analemme de Ptolémée censé être explicatif.
-
Les six arcs de Ptolémée liés à la position du Soleil.
Ce dernier donne ensuite une table où ces valeurs sont tabulées pour un climat (latitude) et une date (longitude du Soleil) donnés[N 5].

Cette table permet d'ébaucher point à point le tracé de cadrans réguliers : horizontaux (à partir des angles descensivus et horizontalis) et verticaux (angles horarius et verticalis), mais cette application n'est peut-être pas le fait de Ptolémée dont le traité nous est parvenu incomplet. Commandin, traducteur et commentateur de Ptolémée, en 1562, s'attela à la tâche… De nos jours, Denis Savoie, sur les pas de Delambre et d'autres auteurs, généralisera la méthode permettant l'application à des cadrans déclinants, inclinés, etc[16].

La méthode trigonométrique « de l'analemme » donnée par Ptolémée a fait long feu. Sa complexité l'a condamnée. Dès le Moyen Âge, d'autres méthodes trigonométriques plus abordables, telle la méthode de Jean Fusoris seront exploitées. Seuls, certains spécialistes oseront l'aborder, comme Commandin, Clavius, Delambre, Denis Savoie.
À l'époque moderne[modifier | modifier le code]
Jean-Domonique Cassini utilisera l'application de l'analemme de Vitruve à une méridienne pour ornementer sa méridienne de Bologne en 1655[17]. Il se servira de la méthode pour visualiser sur la ligne méridienne l'emplacement de plaques indiquant l'entrée de la tache de lumière dans chaque signe du Zodiaque.

À cette époque, des ouvrages traitent du sujet, mais « le terme analemme, dans son sens original de « système de projection », passe au résultat de cette projection[18] », c'est-à-dire au cadran lui-même. On peut citer les ouvrages de Pierre Sainte-Marie Magdeleine (Traité d'horlogiographie, 1657) ou celui d'Ozanam (Récréations mathématiques, 1736).
Aujourd'hui, l'analemme est tombé en désuétude et fait partie de l'histoire de la gnomonique. Seuls quelques gnomonistes utilisant des calculs de trigonométrie sphérique disent se référer à Ptolémée. Ainsi, en 2009, Yvon Massé, membre de la commission des cadrans solaires de la SAF a publié un ouvrage spécialisé, cité en référence, dont le titre est : De l'analemme aux cadrans de hauteur ; il présente une méthode générale de projection et l'application à toutes sortes de cadrans de hauteur créés depuis le XVe siècle jusqu'au XXIe siècle : cadrans horaires, rectilignes, d'azimut.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- En géométrie descriptive, le plan du méridien sera le plan vertical de projection et la ligne méridienne la « ligne de terre ».
- L'arc semi-diurne correspond à la moitié de l'arc diurne soit ici 6 heures
- Le point 4' correspond en fait à la quatrième et à la huitième heure temporaire.
- Ces arcs ou angles sont, dans l'ordre de la table donnée infra : hectemoros, horarius, descensivus, meridionalis, verticalis, horizontalis.
- Cette unique table qui nous soit parvenue faisait peut-être partie d'un ensemble plus vaste couvrant les sept climats principaux et l'entrée dans les différents signes zodiacaux.
Références[modifier | modifier le code]
- Jean-Baptiste Delambre 1817, p. 458 et suivantes.
- Claude Perrault 1684, p. 265.
- Arpad Szabo & Erka Maula 1986, p. 37-55.
- Claude Perrault 1684, p. 265-267.
- Claude Perrault 1684, p. 266 note 4.
- Claude Perrault 1684, p. 266.
- Arpad Szabo & Erka Maula 1986, p. 47.
- Raymond D'Hollander 2002, p. 162
- James Evans, 1999, " The Material Culture of Greek Astronomy ", in Journal of the History of Astronomy, 30 p. 249-251.
- Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne), Livre IX, chap. VIII p. 283… ; voir aussi le texte latin et sa traduction sur le site de Philippe Remacle, Remacle, lire en ligne.
- (en) O. Neugebauer, A History of Ancient Mathematical Astronoy, Berlin, New-York, Hama, ; (de) H. Vogt, Versucht einer Wiederstellung von Hipparchs Fixsternverzeichnis, vol. Astronomische Nachtihten, , p. 224.
- Raymond D'Hollander 2002, p. 160-163
- M. Halma, Composition mathématique de Claude Ptolémée, t. I, Paris, (lire en ligne), livre II, chap. V.
- Voir les notes de Delambre : Jean-Baptiste Delambre 1817, p. 80-82.
- Edité par Heiberg dans Ptolemaei opera astronomica minora, p. 187 sq., Leipzig 1907.
- Denis Savoie, Recherches sur les cadrans solaires : De l'analemme de Ptolémée aux cadrans solaires arabo-islamiques, Turnhout, Brepols, coll. « Travaux de l'académie internationale d'histoire des sciences », , 242 p. (ISBN 978-2-503-55298-9), p. 79-87.
- Voir l'ouvrage de J. D. Cassini : Meridiana
- Éric Mercier et Paul Gagnaire, Cadran Info : Sur le « Petit traité de l'analemme vertical » de M. Le Bourgeoys (1599), vol. 34, Paris, SAF, , p. 57-58.
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 Jean-Baptiste Delambre, Histoire de l'astronomie ancienne, t. II, Paris, (lire en ligne), p. 458.
Jean-Baptiste Delambre, Histoire de l'astronomie ancienne, t. II, Paris, (lire en ligne), p. 458. Claude Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne).
Claude Perrault, Les dix livres d'architecture de Vitruve, Paris, Coignard, (lire en ligne). Arpad Szabo et Erka Maula (trad. de l'allemand), Les débuts de l'astronomie,…, chez les Grecs, Paris, Vrin, , 238 p. (ISBN 2-7116-0911-1).
Arpad Szabo et Erka Maula (trad. de l'allemand), Les débuts de l'astronomie,…, chez les Grecs, Paris, Vrin, , 238 p. (ISBN 2-7116-0911-1).- Yvon Massé, De l'analemme aux cadrans de hauteur, Pontoise, chez l'auteur, , 93 p. (ISBN 978-2-7466-1307-2).